基于改进麻雀搜索算法的锚护机器人逆运动学求解

王瑞君，马祺杰，闫金宝，李红波

（1.中煤华晋集团有限公司王家岭矿，运城 044000；2.中国煤炭科工集团太原研究院有限公司，太原 030006；3.山西天地煤机装备有限公司，太原 030006）

当下求解逆运动学最常用的3 种方法分别是数值计算法[1]、代数公式法[2]和几何分析法[3]。拆解分析法和几何分析法求解逆运动学时需要考虑Pieper准则。随着机器人功能与结构的飞速发展，逆运动学的求解过程更加复杂，普通的求逆解方法有可能求不出解来。因此学者们将神经网络、优化算法等智能化求解工具运用于求逆解的过程中。其主要思路是将机器人求逆问题转化成多元多峰函数求最值问题[4]。主要有遗传（Genetic Algorithm）算法[5]、粒子群（Particle Swarm Optimization）算法[6]，以及BP神经网络（Back Propagation）算法[7]等。

文献[8]提出一种引入CMA-ES 步长更新的改进Particle Swarm Optimization 算法求机器人逆运动学解；文献[9]将没有冗余度技术的机器人关节空间分为8 组唯一域，并用数值法求解；文献[10]则给出了一种由布谷鸟算法和牛顿法组合的算法求解逆运动学。

文献[11]针对SSA 算法迭代后期种群多样性小，全局寻优能力差等问题提出一种融合柯西变异和反向学习的优化麻雀算法。经过多次多种的对比试验，得到的结果表明改进麻雀算法的极限逼近速度更快、误差更小，全局寻优能力更强。基于此，本文给出了一种改进麻雀搜索算法ISSA（improved sparrow search algorithm），以解决基本的麻雀搜索算法在求解过程中极限逼近速度慢、全局寻优能力差等不足。该算法的第1 步，先通过反向学习策略生成初始种群，增加多样性；第2 步，引入柯西-高斯变异提高算法的全局寻优能力；最后将ISSA 应用到求锚护机器人逆向运动学解中。

以CMM2-24 锚护机器人为例，使用指数积公式搭建运动学模型，将锚护机器人求逆解问题转化成麻雀算法迭代求极值问题。然后分别从机器人的位置、姿态以及位姿3 个方面建立适应度函数来进行仿真实验。以此来检验算法改进的实施性。

1 麻雀搜索算法

麻雀搜索算法是根据麻雀种群捕食并规避掠食者的行为规律得到的一种群智能优化搜索算法[12]。在麻雀搜索算法中，每代探索者位置更新如下：

式中：β 是一个服从N（0，1）的随机数；K∈［-1，1］表示移动方向；添加极小值c 是为了分母不为0；fi是第i 只麻雀的适应度值；fg和fw分别是当前阶段种群的极小、极大适应度值。

2 改进麻雀搜索算法

2.1 反向学习策略

反向学习[13]可以使得到最优解的概率提高，其主要思想是，通过反向学习寻到当前解对应的反向解，然后经过对比保留更好的解。其数学模型：假设p=［x1，x2，x3，…，xn］为n 维空间一个点，其中xi∈［ai，bi］，i=1，2，…，n，则反向点p′=［，，，…，xn′］其中=ai+bi-xi。

2.2 高斯扰动和柯西扰动

在迭代寻优过程中，把寻到的初始解进行高斯扰动[14]，公式为

式中：p 为初始解；N（0，1）是个随机数，该数服从高斯分布特性。柯西变异来源于柯西分布，一维柯西分布概率密度如下[15]：

柯西扰动类似于高斯扰动，扰动公式为

式中：C 表示柯西分布的随机数。柯西分布随机变量生成函数为

柯西分布有着较好的两翼概率，极大地提高了局部抗干扰能力和整体搜索寻优能力。高斯分布的特性则是当前个体附近区域的扰动性好，所以它的局部搜索能力强。根据两者的优缺点，本文在使用麻雀算法求逆解时先加入柯西扰动加大搜索范围，提高算法的全局寻优能力，后期投入高斯扰动增强局部搜索能力，减少算法的迭代搜索时间。

3 改进麻雀搜索算法在锚护机器人逆向运动学分析中的应用

3.1 正向运动学建模

CMM2-24 锚护机器人的三维模型如图1 所示。可知锚护机器人是个经典的球腕型结构。为了便于理解和求解该结构的运动学模型，可以把6 个关节三三分类，前3 个关节确定位置，后3 个关节确定姿态。

图1 CMM2-24 锚护机器人Fig.1 CMM2-24 anchorage robot

CMM2-24 锚护机器人的结构简图如图2 所示，采用螺旋理论[16]搭建运动学模型。

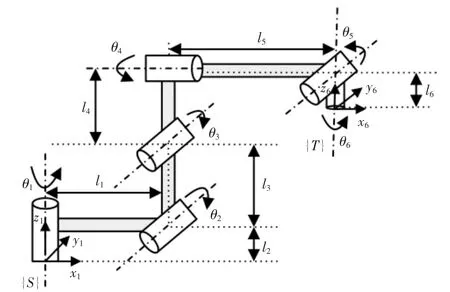
图2 锚护机器人结构简图Fig.2 Schematic diagram of anchorage robot

正运动学建模的关键参数如表1 所示。其中w表示轴线向量，r 表示轴线上的一点，i 表示关节序号。

表1 机器人各关节螺旋轴Tab.1 Spiral axes of each joint of robot

机器人的工具坐标系建立在最后一个关节处，机器人工具坐标系的初始位姿为

锚护机器人的正向运动学的指数积公式（POE）为

3.2 构建适应度函数

本文使用锚护机器人的位置、姿态、位姿这3种参数分别设置各自的适应度函数[17-18]：

式中：pdes和pcur分别为目标和实际的位置；zdes和zcur分别为目标和实际的姿态；f3为目标与实际的位姿误差；α 和β 分别为位置矢量P 和姿态矢量的权值系数。使用构建好的适应度函数求锚护机器人逆运动学解的流程，如图3 所示。

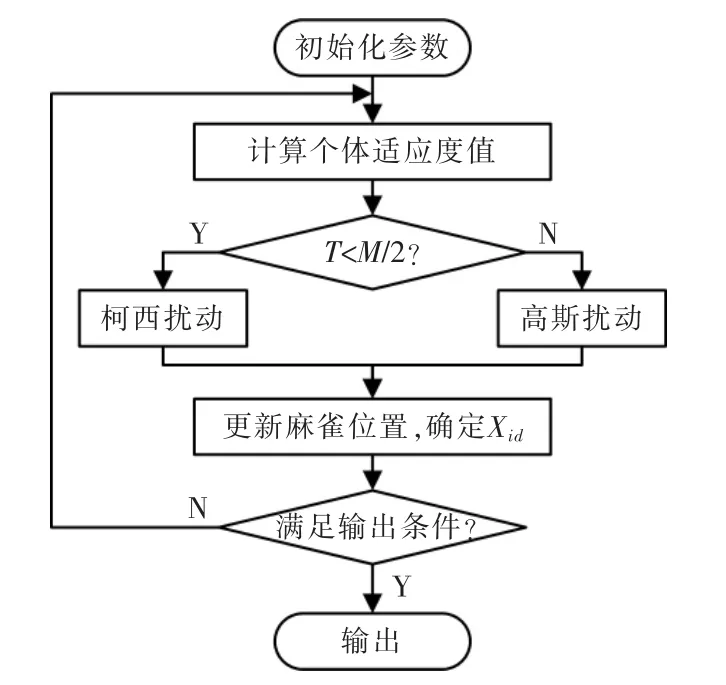
图3 ISSA 求解流程Fig.3 ISSA solution flow chart

4 仿真实验与结果分析

分别采用ISSA 与SSA 对锚护机器人的位置、姿态、位姿3 个方面进行仿真实验，以此来验证改进后的算法求解锚护机器人逆运动学时的可行性与有效性。

4.1 初始参数设定

对算法进行多次试验后取最佳性能的初始参数：种群个数均为Size=50；均进行150 次迭代；探索和侦察预警者个数初始值均为种群总数的20%；各关节角范围为［-π，π］；α=0.0033，β=1；当迭代次数maxgen=150 或f<10-5时，算法结束。

4.2 位置仿真

对锚护机器人进行位置仿真实验，设初始角（rad）为Q1=［1；0.5；2；1；1；-0.5］，锚护机器人的末端解析值位置为P1=［3452.08984；537.09178；2920.03420］。分别将ISSA、SSA 各自求解100 次，结果与解析值对比后得到2 种位置误差进化曲线，如图4 所示。

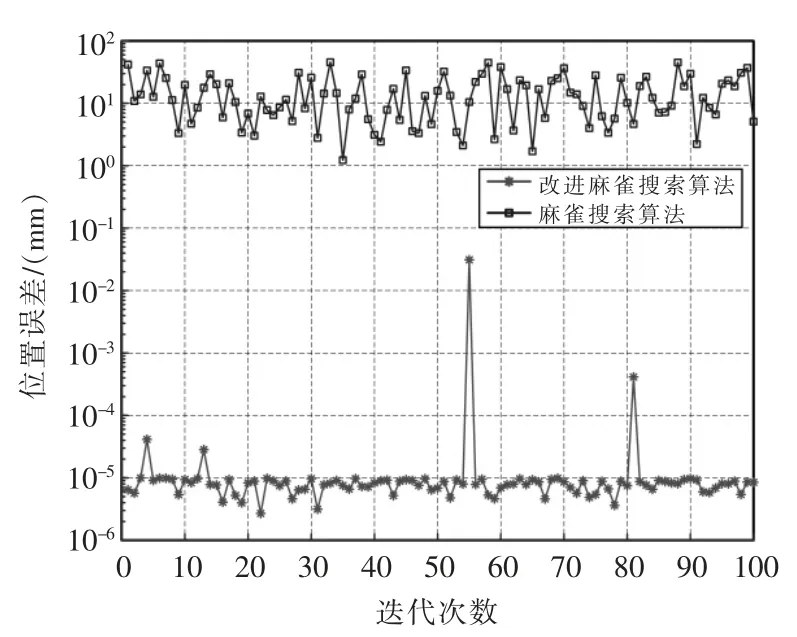
图4 位置误差进化曲线Fig.4 Evolution curves of position errors

结果表明在位置误差上，SSA 算法的收敛精度保持在10～102之间，而ISSA 算法的收敛精度则保持在10-5～10-6之间，由此证明ISSA 比SSA 收敛精度更高。

ISSA、SSA 独立运行100 次的位置误差，如表2所示。其结果表明，ISSA 在平均值上比SSA 提高了5 个数量级，在标准差上则提高了4 个数量级。

表2 位置误差对比Tab.2 Position error comparison

4.3 姿态仿真

对锚护机器人进行姿态仿真，设初始角（rad）为Q1=［1；0.5；2；1；1；-0.5］，分别将ISSA、SSA 各自求解100 次，所得2 个算法的姿态误差如图5 所示。

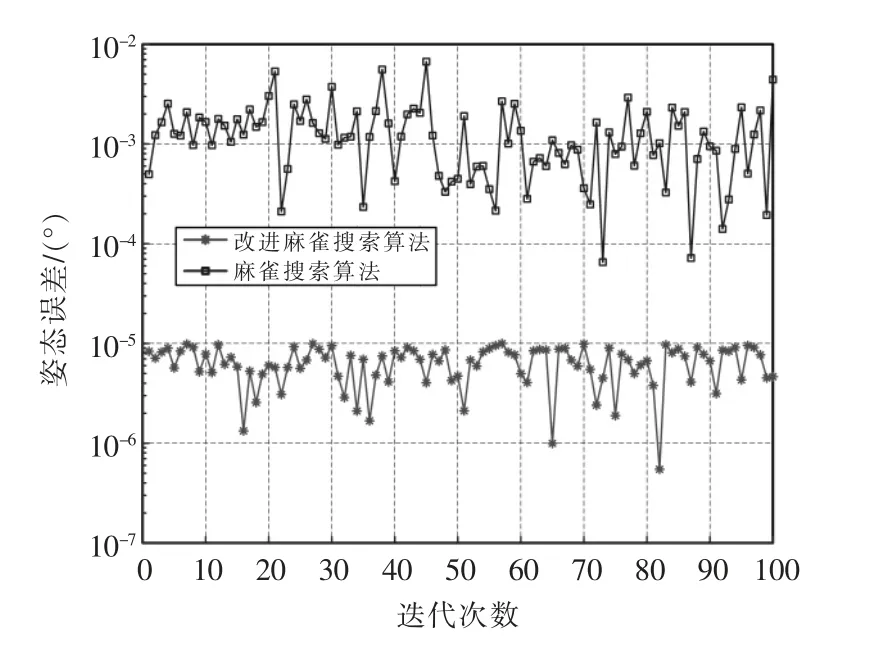
图5 姿态误差进化曲线Fig.5 Evolution curve of attitude error

结果表明对于姿态误差，SSA 算法的收敛精度保持在10-3，而ISSA 算法的收敛精度则保持在10-5。证明ISSA 的收敛精度更高，鲁棒性好。

ISSA、SSA 独立运行100 次的姿态误差如表3所示，结果表明，ISSA 在平均值和标准差比SSA 均提高了3 个数量级。

表3 姿态误差对比Tab.3 Comparison of attitude error

4.4 位姿仿真

给定关节角θ（rad）=［1，2，1，-1，0.5，-0.5］，代入式（9）求得位姿矩阵T：

根据已知末端位姿，代入式（14），两种算法设置相同的参数，分别进行逆向运动学分析，其结果如表4 表示。

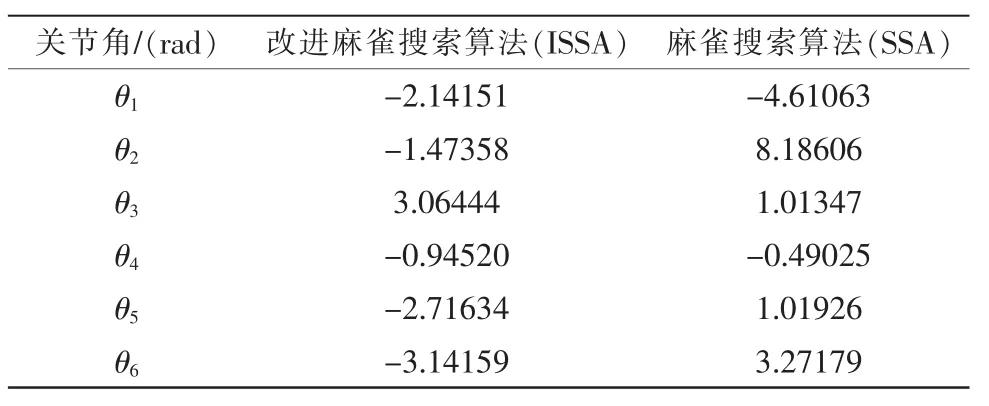
表4 逆运动学解对比Tab.4 Inverse kinematics solution comparison

两种算法分别对位姿进行求解得到的误差曲线，如图6 所示。结果显示ISSA 的收敛精度明显提高，SSA 在100左右就停止了搜索。对图6 中2 条位姿误差曲线的斜率进行对比分析，则不难看出ISSA在刚开始迭代的时候有着比SSA 更强的局部及全局搜索能力。

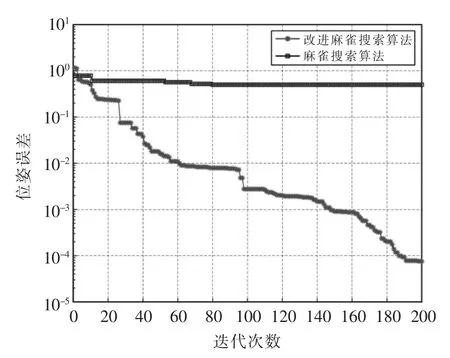
图6 两种算法位姿曲线对比Fig.6 Comparison of pose curves of two algorithms

5 结语

针对锚护机器人求逆解问题，本文提出一种结合柯西-高斯变异的改进麻雀搜索算法（ISSA），相对于传统麻雀算法（SSA），该算法避免了种群单一、鲁棒性差的缺点。将ISSA 和SSA 分别应用到求锚护机器人逆解中，并对其位置误差、姿态误差以及位姿误差3 个方面分别建立适应度函数进行对比仿真实验。使用位置误差做适应度函数时，ISSA 比SSA 高5 个量级的收敛精度和4 个量级的稳定性。使用姿态误差作为适应度函数时，ISSA 比SSA 高3个量级的收敛精度。使用位姿误差做适应度函数时，ISSA 比SSA 高5 个量级的收敛精度。实验结果表明：改进麻雀搜索算法拥有收敛精度高、速度快、稳定性好等特点，因此充分证明了算法改进的可行性。