计及电动汽车的综合能源系统优化调度

邵文锋，聂祥论，阚 超

（贵州大学 电气工程学院，贵阳 550000）

人类社会的发展离不开能源，然而传统化石能源不仅面临着枯竭的风险也对环境造成了恶劣的影响。在这样的背景下，我国提出“力争在2030 年前达到碳排放峰值，在2060 年前实现碳中和”的双碳目标，并积极开发风力和光伏等可再生能源。然而可再生能源具有较强的随机性和波动性，IES 由于能够通过加强能源间的耦合作用来促进消纳可再生能源，成为当前极具前景的发展方向。文献[1]考虑综合需求响应，建立多能源IES 日前经济调度模型。文献[2]引入碳捕集装置，提出积极需求响应和碳交易机制的IES 规划模型。文献[3]计及能量互济，提出一种区域IES 优化调度策略。

此外，最近几年EV 数量增长速度较快，制定合理的调度策略成为EV 研究的重要问题之一。文献[4]以减小负荷波动率和提高运营商效益为目标，提出有序充电控制策略。文献[5]采用不间断充电方式，为降低配电网负荷曲线峰谷差和EV 用户充电成本，提出一种有序充电策略。文献[6]以促进消纳可再生能源和降低EV 充电成本为目标，建立一种制定EV 动态充电电价的模型。但上述文献未考虑EV 通过V2G（vehicle-to-grid）技术进行有序放电的场景，这种模式下EV 能够响应系统需求进行充放电，从而削峰填谷[7]、缓解系统峰时段供能压力[8]、降低系统调度成本[9]。

鉴于此，本文以计及EV 有序充放电的IES 为研究对象，基于分时电价综合考虑供需双方利益，构建日前优化调度模型。最后，通过算例仿真对比验证模型的有效性。

1 综合能源系统

1.1 综合能源系统结构

本文构建的IES 包括供电、供热和供冷系统，能够满足各类负荷需求，其模型和能量流动情况如图1 所示。

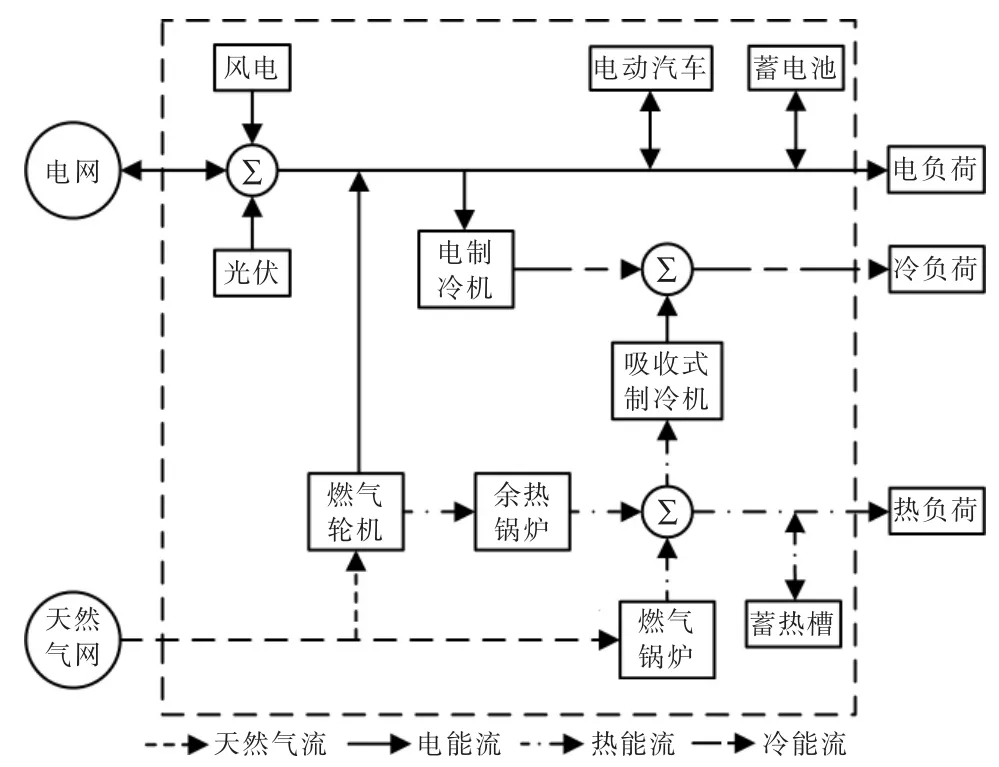
图1 综合能源系统结构图Fig.1 Structure of integrated energy system

1.2 EV 出行特性

为方便计算，将一天离散化为24 个时段，每个时段长为1 h。根据研究，在建模时认为居民区用户回家时将EV 接入电网、次日出行时离开。根据美国交通部对全美家庭用车的调查结果，通过数据拟合可近似认为居民区内EV 返程和起程时间分别符合式（1）和式（2）：

式中：μe＝9.24；σe＝3.16。

同时，日行驶里程服从对数正态分布，其概率密度函数如下所示：

2 综合能源系统优化调度模型

2.1 目标函数

日前调度阶段，以系统日运行总成本最小为目标函数，如下所示：

式中：Fgas、Fom、Fgrid和FEV分别为系统购气成本、运维成本、电网交互收益/成本和EV 交互收益/成本。

系统购气成本为

式中：fgas，t为t 时段天然气单价；VGT，t、VGB，t分别为t时段燃气轮机和燃气锅炉消耗的天然气体积。

系统运维成本为

式中：Fn为设备的单位维修成本；为t 时段设备n 的输出功率。

电网交互收益/成本为

EV 交互收益/成本为

2.2 约束条件

2.2.1 功率平衡约束

电功率、热功率、冷功率平衡约束为

式中：Pwt，t、Ppv，t和PGT，t分别表示风机、光伏和燃气轮机 输出电功率；QWHB，t、QGB，t分别表示余热锅炉和燃气锅炉输出热功率；PAC，t、PEC，t分 别表示吸收式制冷机和电制冷机输出冷功率；Pbat、PHST，t分别表示 蓄电池和蓄热槽各自输出的电功率和热功率，为负则代表充能；EEC，t、QAC，t分别表示电制冷机和吸收式制冷机输入电功率和热功率；Le，t、Lh，t、Lc，t分别表示电、热、冷负荷功率。

2.2.2 设备运行约束

（1）能量转化设备约束

（2）储能设备运行约束

（3）EV 运行及出行约束

每辆EV 均需满足如下约束，EV 整体始末时刻满足能量守恒约束：

此外，EV 作为交通工具还需满足出行需求和出行时间约束：

（4）外网约束

3 算例分析

为验证本文所提考虑EV 有序充放电的经济调度策略的效果，本文利用图1 结构来设置算例。本算例中含100 辆EV，电池容量均为35 kWh，充放电功率上限均为7 kW，其入网初始荷电状态（state of charge，SOC）服从正态分布，假设其入网后，智能充电装置收集用户次日出行时间和出行所需电量，并将信息上传。系统控制中心可以根据可再生能源及负荷的预测数据，和所有EV 的出行信息制定日前调度计划。IES 相关设备参数见文献[10]。仿真时间为24 h，仿真步长为1 h。

3.1 算例参数

IES 与大电网交互的分时电价如表1 所示，其中的购电、售电电价也分别是EV 充电、放电电价。分时气价如表2 所示。电、热、冷负荷曲线如图2 所示。

表1 分时电价Tab.1 Time of use price

表2 分时气价Tab.2 Time-sharing gas price

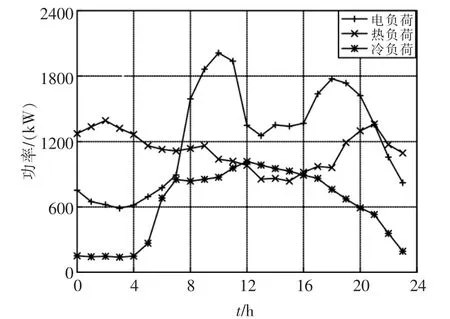
图2 电、热、冷负荷曲线Fig.2 Electric，heat and cooling load curves

为分析引入EV 对系统经济性的影响，本文设置3 种对比方案进行算例仿真。

方案一：考虑EV 无序充电负荷的IES 优化调度。EV 从返程到家就接入电网全速充电，满足充电电量为下次行驶所需后即停止。

方案二：计及EV 有序充电的IES 优化调度。EV 尽可能在谷时段进行有序充电，在谷时段无法充到所需电量时再考虑平、峰时段。

方案三：计及EV 有序充放电的IES 优化调度。在方案二的基础上，EV 响应IES 调度，在平、峰时段可进行有序放电。

3.2 优化结果分析

通过算例运行，可得不同方案EV 调度结果如图3 所示。不同方案系统运行成本对比、EV 用电成本对比分别如表3、表4 所示。

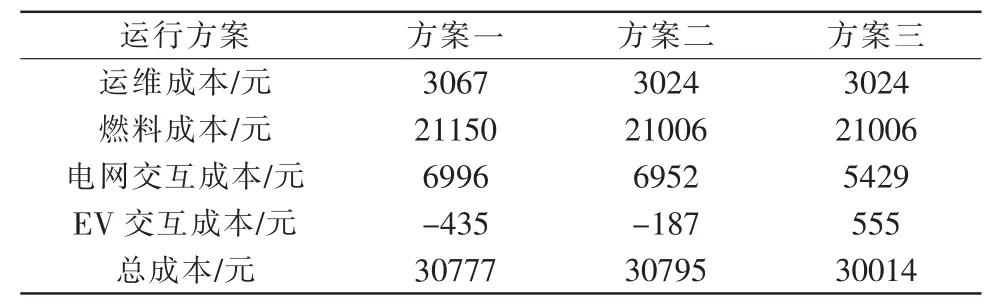
表3 各方案系统运行成本对比Tab.3 Comparison of system operation costs by option

表4 各方案电动汽车用电成本对比Tab.4 Comparison of EV power consumption costs by option

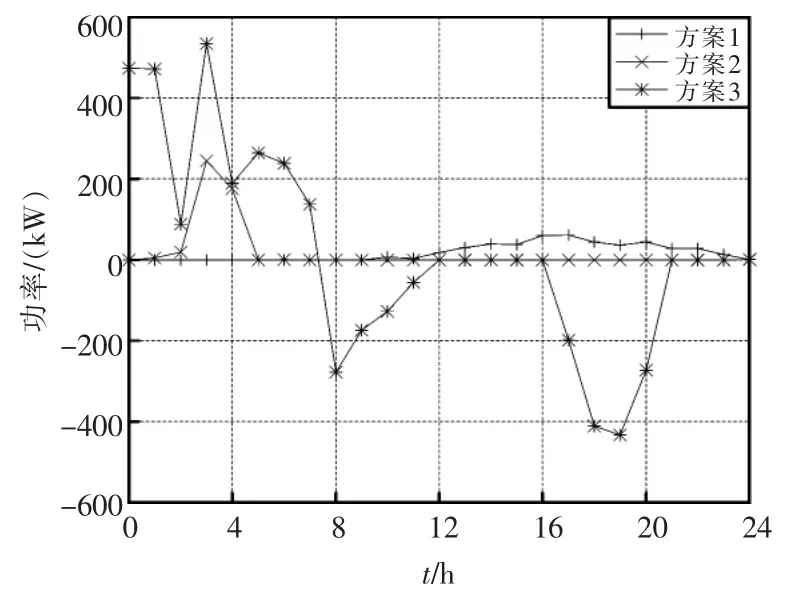
图3 电动汽车功率曲线Fig.3 EV power curves

由图3 可知，方案一中EV 充电负荷在16∶00～20∶00 时处于高峰时段，即此时是用户返程高峰期，而该时段电负荷曲线也处于晚高峰时期，因此无序充电方案直接导致“峰上加峰”现象。随着EV 的普及，这种现象还会加剧，将会给系统功率平衡带来新的困难。

方案二与方案一相比，从经济性上看，IES 调度总成本提升18 元，EV 用户充电成本降低248 元，即IES 和EV 用户总成本降低230 元；从负荷曲线上看，方案二EV 的充电负荷主要转移到3∶00～4∶00，此时基础电负荷处于低谷，即方案二可以平缓负荷曲线，促进消纳可再生能源。因此方案二IES 提升少量成本，但是大幅降低EV 用户充电成本，同时降低系统峰谷差，可以有效促进负荷低谷期间对可再生能源的消纳能力，即随着系统可再生能源装机量的提升，方案二的成本将会低于方案一。

方案三与方案二相比，EV 大幅提升谷时段的充电量，共计充电1007 元，并集中在8∶00～11∶00 和17∶00～20∶00 大量放电，这2 个时段系统电负荷均处于高峰。即方案三不仅降低IES 调度成本，平滑负荷曲线，降低峰谷差，而且降低EV 用户充电成本。

随机抽取3 辆EV，编号为1、2、3，将相关电量均转化为对应荷电状态，其信息如表5 所示。

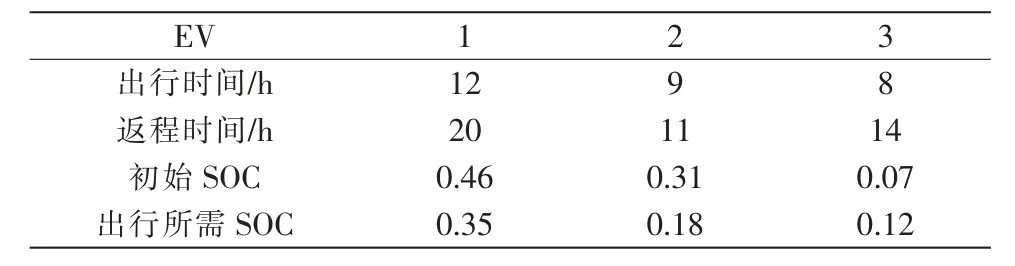
表5 电动汽车出行信息Tab.5 EVs travel information

3 辆EV 返程入网即按照出行所需SOC 更新其荷电状态，其整日的荷电状态变化情况如图4 所示。

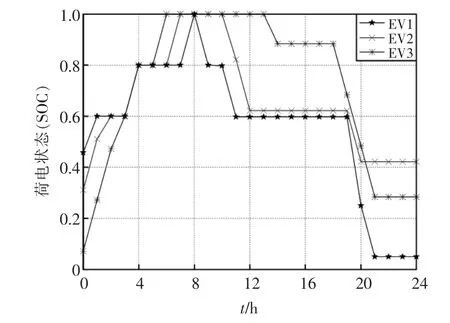
图4 电动汽车荷电状态Fig.4 SOC of EVs

由图4 可知，每辆EV 在离开电网时的SOC 均大于其出行所需SOC，且整个调度过程功率和能量都满足实际约束，即本文策略能够在降低EV 用户用电成本的同时，兼顾其出行需求和EV 蓄电池寿命，从而有效激励EV 用户响应有序充放电策略。

方案3 与方案1 相比，在保障EV 用户出行需求的基础上，降低IES 调度成本763 元，降幅为2.48%，降低EV 用电成本990 元，降幅达227.59%，同时电负荷峰谷差从70.98%下降为62.41%，降幅为12.08%。综上所述，本文所提的方案3 兼顾供需双方利益，取得了预期的效果，具有可行性。

4 结语

随着EV 普及，电力系统会遭遇新的挑战，同时也会迎来新的机遇。为满足EV 不断增长的充电需求，同时充分利用EV 作为储能单元灵活充放电、消纳可再生能源的潜力，本文基于分时电价提出一种计及EV 有序充放电的IES 优化调度策略。经算例验证，该策略既能够削峰填谷、降低系统调度成本，还可以在兼顾EV 用户出行需求和EV 蓄电池寿命的前提下为EV 用户提供大量收益。