基于FPGA的转台分度误差分离电路研制

马瑞翔,朱 进,黄 垚,朱维斌,薛 梓

(1.中国计量大学计量测试工程学院,浙江杭州 310018;2.浙江省计量科学研究院,浙江杭州 310019;3.浙江大学光学科学与工程学院,现代光学仪器国家重点实验室,浙江杭州 310027;4.中国计量科学研究院,北京100029)

0 引言

转台是进行全圆周角度连续测量的常用设备,搭载高精度圆光栅的角度编码器,广泛应用于精密工业、国防军工等领域[1]。转台定位精度受编码器圆光栅刻线误差、安装误差等静态因素以及主轴误差运动、机械老化与形变、环境条件等动态因素的影响。为保障转台定位精度,需要对转台测角误差进行校准,以角度编码器为转台的测量反馈装置,转台测角误差包含转台自身误差和编码器误差,其中最主要的是分度误差[2]。针对转台分度误差的分离,主流方法为硬件分离与数值分离。

文献[3]采用分组不等间距排布读数头方式,通过17个读数头对细分误差、刻线误差进行检测,角度编码器的测量误差减小到0.036″。文献[4-5]通过12读数头3-4-7不等间距排布方式实现自校准转台设计,实验表明定位精度优于0.1″,重复性可达0.3″;文献[6-7]开发了基于3-4读数头排布方式的自校准角度编码器系统,定位精度在±1.5″内,重复性优于1.1″,并利用全组合和EDA的混合测角校准的误差分离方法,提高了EDA法自校准精度,装置的测量不确定度达到0.05″(k=2)。文献[8]提出一种谐波模型来描述圆光栅安装引起的误差,使用精度和角分辨力高的激光陀螺仪在线测量编码器的误差,校准精度可达到0.1″。文献[9]结合压缩感知和稀疏分解来分离圆光栅测角误差,使用谐波补偿前10阶误差,测量误差减小了97%。文献[10]针对圆光栅安装不当引起的测角误差,采用多齿分度台和自准直仪进行校准,最大误差由114.4″降低到1.8″。

综上,基于多读数头的硬件分离法,分离精度高但需要较多的空间用于安装特定数量的读数头,对各读数头的一致性都有较高的要求,存在结构复杂、成本高等问题。数值分离法需要高精度角度参考标准,需要在转台设计时预留安装空间,安装也会引入额外误差。因此,不依赖外部参考标准的转台分度误差的分离方法,成为研究重点。

本文关注转台测角系统精度,针对转台分度误差分离开展研究。对傅里叶法分离转台分度误差原理进行阐述,基于FPGA平台研制转台多通道角度信号采集电路,根据误差分离任务需求对电路中信号同步采集、数据传输电路进行说明,最后通过转台实验证明了电路功能的有效性和转台分度误差分离方法的有效性。

1 基于傅里叶法的转台分度误差分离原理

转台测角系统主要由转台和编码器组成,编码器包括圆光栅、读数头和细分盒。图1为光栅圆周共M个读数头的安装示意。

图1 多读数头安装示意图

读数头Hd、Hq相对于H1的安装角度位置为αd、αq(α1=0),在转台旋转过程中,读数头测量值还受到分度误差ε(θ)的影响,读数头Hq测量值如式(1)所示:

Hq(θ)=θ+εq(θ)=θ+ε(θ+αq)

(1)

式中θ为转台实际转角,对所有读数头均相同。

由于读数头的安装角度位置αq,转台分度误差具有一个相移。通常式(1)中会包含一个直流偏置,测量后可以消除,在本文中不做讨论。

任意两读数头同时刻的测量值相减,得到的角度差值可消除未知的转台实际转角θ,如图2所示。

图2 转台分度误差产生示意图

图2显示了因圆光栅安装偏心引起的分度误差,在整圆周存在以2π为周期的误差曲线。

δdq(θ)=Hd(θ)-Hq(θ)

=ε(θ+αd)-ε(θ+αq)

(2)

式中1≤q≤d≤M。

由于圆周封闭原则,分度误差ε(θ)是周期性函数,因此δdq(θ)也是周期性函数,ε(θ)用傅里叶级数表示为

(3)

式中N为圆周等分角的数目。

傅里叶系数F(n)可表示为

(4)

为了从式(2)中获得转台分度误差,由测量值得到的角度差值δdq(θ)需要从时空域转换到频域。根据信号理论,时空域信号的傅里叶级数具有空间位移和线性两个重要性质。通过离散傅里叶变换(DFT),式(2)可以写成

Edq(n)=(einαd-einαq)F(n)=Wdq(n)F(n)

(5)

式中:Edq(n)为角度差值函数δdq(θ)的傅里叶系数;Wdq(n)定义为F(n)到Edq(n)的传递函数。

若Edq(n)和Wdq(n)的值已知,则转台分度误差ε(θ)的傅里叶系数F(n)可计算得到:

(6)

因此转台分度误差ε(θ)可通过使用离散傅里叶逆变换(IDFT)来获得。

2 多通道角度信号采集与传输电路

2.1 电路方案设计

转台分度误差分离的关键是在于获取全圆周内同一时刻的多读数头角度测量值,转台测角系统输出的整圆周角度测量值的显著特点是大数据量,如何高质量地获取大数据量的整圆周角度测量值是转台分度误差分离任务的关键环节。

FPGA具有并行工作、IO资源丰富、设计灵活等优点,可以承载转台测角系统整圆周角度测量值采集任务。电路原理图如图3所示。

图3 多通道角度信号采集与传输电路结构

转台测角系统工作时读数头信号经细分盒转换成增量差分方波,差分方波经信号采集模块转换成M路角度测量值H1(θ)、…、HM(θ),经同步采集模块以设定的采集速率至以太网传输模块,实时传输到上位机中,简化硬件设计和逻辑开发。

2.2 关键问题分析

2.2.1 多通道信号同步采集

同步采集频率根据转台测角系统输出的增量差分方波频率设计,方波频率与转台转速以及角度传感器有关,以本文实验用到的编码器为例设计,编码器型号参数见表1。

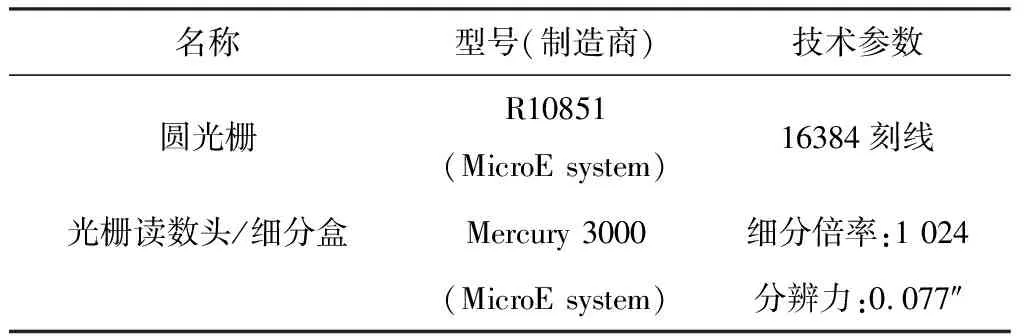
表1 转台编码器参数

相关文献指出[11],误差谐波总阶次N=50即可满足应用精度要求。参考奈奎斯特采样定律和工程要求,全圆周采样点数取100倍误差阶次N,即全圆周采样点数Ks≥5 000。

数据同步采集模块根据参数instruction调节频率控制字K,对输入进来的多路读数头信号进行同步采集,图4为数据同步采集模块的RTL级仿真电路图。

图4 数据同步采集模块

FPGA时钟选用100 MHz晶振,精度为±20 ppm, FPGA内以状态机的方式产生采集方波,状态机计算采集方波的准确性直接影响测角间隔,进而会影响误差分离效果。为消除组合逻辑输出不稳定和毛刺隐患,使用同步寄存器输出,选择三段式状态机,以差分方波发送。同步采集状态机工作模拟图如图5所示。

图5 数据同步采集状态机模拟图

IDLE为初始状态,作为采集模块的开始,将模块中的各参数以及状态转换的信号进行初始化。IDLE状态结束后,发送一个cnt_start信号,同时跳转到S1(CLK_CNT)状态,启动时钟计数器。此时每个时钟上升沿,时钟计数器clk_cnt+1,当时钟计数器clk_cnt=频率控制字K时,CLK_CNT状态结束,跳转到S2(READY)状态。READY状态用于数据采集前的等待,消除时钟偏斜等带来的影响,持续2个时钟后跳转到S3(SAMPLE)状态。在SAMPLE状态下进行多通道的数据同步读取并将数据储存到多个临时寄存器reg_temp(M)中。SAMPLE状态结束后跳转到S4(SAMPLE_DONE)状态,表示一次数据同步采集完成,并将采集的数据从寄存器reg_temp(M)发送给以太网传输模块,之后跳转到IDLE状态进行下一次数据采集。

2.2.2 以太网传输

为了保证数据传输的可靠性,需要选择可靠、不丢数的协议进行传输,选择TCP/IP协议栈在FPGA上构建socket服务器,上位机为客户端完成数据通信。搭建Intel FPGA软核Nios II,在Nios II SBT for eclipse中选择MicroC/OS-II RTOS和NicheStack TCP/IP协议栈软件组件,从而完成百兆网络系统应用程序,选择SDRAM作为Nios II的数据/指令运行存储器,节约FPGA资源。TCP/IP通信过程如图6所示。

以系统设计的最高同步采集频率20 kHz为例,6路编码器细分盒的角度测量值数据传输速率为3.84 Mbit/s,百兆以太网完全满足应用。

3 实验与数据分析

为验证多通道角度信号采集与传输电路功能有效性和转台分度误差分离方法的有效性,使用实验室自制多通道角度信号采集与传输电路完成信号采集任务。选用EP4CE115F29C7作为电路主控芯片,AM26LV32作为差分转单端芯片,IS42S16320B作为SDRAM存储芯片,RTL8211作为以太网芯片,SN74LVCC3245作为差分信号驱动芯片。多通道角度信号同步采集与传输电路(DASA_B)实物如图7所示。

以中国计量科学研究院研制的转台测角系统为平台开展实验,实验平台示意图如图8所示。其中激光陀螺测角仪的零起分度误差为±0.5″,重复性优于0.3″,转台测量重复性为0.3″。

图8 实验平台示意图

为了分析比对不同角度间隔下的转台分度误差分离效果,实验中转台读数头采用3-4布局,一组为3读数头等分排布,另一组为4读数头等分排布,两组间存在一个共用读数头。以便获得多组不同夹角分布的读数头数据。读数头分布如图9所示。

图9 实验转台六读数头排布示意图

不同角度间隔下分离分度误差时域图如图10所示。图10(a)中,以激光陀螺测角仪为参考得到的1号读数头分度误差曲线ε1_R,峰峰值为60.9″。以角度间隔为180°、150°、90°、30°的两读数头应用傅里叶法得到分度误差曲线ε1_180°、ε1_150°、ε1_90°、ε1_30°,为了方便分析,ε1_R已去掉直流量;图10(b)中,显示了应用傅里叶法求取的分度误差与以激光陀螺测角仪为参考的ε1_R之差。

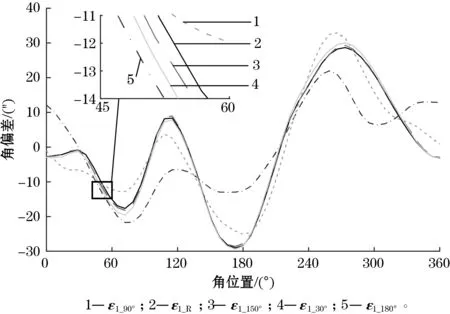
(a)不同角度间隔下分离分度误差图

为了更加直观地分析残留误差,取整圆周的分度误差ε1_R与残留误差ε1_180°-ε1_R、ε1_150°-ε1_R、ε1_90°-ε1_R、ε1_30°-ε1_R作谐波阶次分析,分析结果如图11所示。

图11 残留分度误差谐波阶次图

由图11可知,转台分度误差的1～6次谐波明显,大于1″。可以看出,ε1_180°-ε1_R以偶数次谐波为主、ε1_90°-ε1_R以4次谐波为主,与EDA法中双等分、四等分布局效果类似。不同角度间隔下分离误差后残留分度误差的峰峰值如表2所示。可以看出150°的效果最好,与图11中的谐波阶次幅值相对应。

4 结束语

本文对转台测角系统测角误差中最主要的分度误差分离展开研究,误差呈谐波分布,阐述了基于傅里叶法的分度误差分离原理。针对分离任务中的大数据采集,开发了基于FPGA的多通道角度信号同步采集与传输电路。在3-4布局的转台测角系统中进行实验,结果表明:不同角度间隔下的双读数头,均可以应用傅里叶法分离转台分度误差,其中角度间隔为150°的双读数头分离效果最佳,将峰峰值为60.9″的误差减小至2.19″。本文的研究成果能够为转台测角系统中分度误差的分离提供理论依据和硬件支撑。