一种低功耗高精度的正弦编码器细分算法

郝祥印,苏志刚,张亚娟

(中国民航大学中欧航空工程师学院,天津 300300)

0 引言

正余弦编码器因可携带丰富的位置信息而被广泛应用于高精度位移/角度测量。目前常用的正余弦编码器主要有2种:光栅编码器和磁栅编码器。光栅编码器价格昂贵、对环境要求严苛;依靠霍尔效应的磁栅编码器的抗环境干扰能力强,可提供无接触式位移测量,且价格相对低廉,因此得到了广泛的应用。物联网集成度的提高对磁编码器的整体性能提出了进一步的要求,即在保持精度或提高精度的前提下降低功耗,以最大化设备运行时间,因此需要降低MCU的功耗并使用一种高效、高精度的细分算法以保证磁编码器性能。

文献[1-3]提出使用最小二乘估计来进行误差校正,但这种方法计算量大,不适合应用在实时位移测量中,文献[4]中使用两级级联卡尔曼滤波器进行误差校正,文献[5-6]中分别使用神经网络和粒子群来进行误差模型中各项参数的估计,计算复杂,参数收敛时间长;文献[7]使用正交全数字锁相环来消除误差,但不能处理谐波,文献[8-10]通过增加滤波器来提供谐波抑制能力,但使用的都是二阶锁相环,在频率斜坡输入下存在稳态误差。

以上算法由于计算量大、参数收敛时间长、不能有效处理谐波误差等原因,不适合在低功耗场合下使用。本文首先分析了磁编码器的工作原理及各种误差源,建立了包含磁栅尺磁场畸变的误差模型;其次,以误差模型为理论基础,根据误差模型中各参数的特点,提出了一种适用于低功耗场景下的低计算量的细分方法:使用离线数据构建的查找表进行幅值不等、相移以及谐波的抑制,使用频域处理的方法消除信号中的畸变误差;最后通过实验验证了算法的有效性。

1 磁栅编码器的工作原理

磁栅编码器的结构如图1所示,包含一个与移动部件相连的读数头以及一个固定不动的磁栅尺,其中磁栅尺上录制有磁极距(λ)相等的正弦形式的磁场,当读数头相对于磁栅尺运动时,读数头以90°相差的形式输出±sin和±cos 2组差分信号[5],差分后变为

(1)

式中:A为输出信号的幅值;θ为当前的角位置,θ=x/λ×2π;x为位移;下角标s表示sin,下角标c表示cos,此标注方式全文通用。

2 误差建模

误差建模是本文所提出算法的理论基础,这一部分将对各种误差进行分析和建模,得到一个包含各种误差的信号模型。式(1)为理想情况下读数头的输出信号,然而实际输出信号会受到各种因素的影响。误差源可归结为以下几种:读数头误差、磁栅尺磁极距λ不等、磁场强度不等、磁栅尺磁场畸变、电路误差以及噪声等[4-5,8,11-12]。

2.1 读数头误差

读数头内部的4个霍尔元件之间的间距为(m+1/2)λ/2,m∈N,然而实际制造过程中,霍尔元件存在中心偏移并且霍尔元件在PCB板上焊接时也存在位置误差,导致4个霍尔元件之间的距离出现误差,形式如图1所示,以sin+霍尔为参考,其余3个霍尔元件存在单侧移动、同侧移动、对侧移动误差以及这几种误差的组合,不失一般性的可以用如下表达式描述:

(2)

式中:Us+为sin+霍尔的输出信号,其余同理;φi为相应霍尔元件的位置误差,i∈[1,4]。

2.2 磁极距不等

磁栅尺在录磁时,由于热致伸缩以及录磁机本身的定位精度问题会导致磁栅尺的磁极距并非处处相等,如图2所示。

图2 磁极距不等

每个磁极距都有微小的误差,假设每个磁极距内都是标准的正弦波,读数头以速度v0匀速运动,此时霍尔sin+的输出信号为

=sin[2π(f+δfi)t-δφi]

(3)

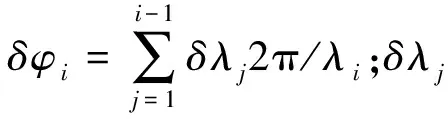
由式(3)可知霍尔sin+的输出信号中除了包含目标信号外,还包含一个频差项以及一个相差项,频差项是由当前位置的磁极距误差产生的,而相差项是由磁极距不等的误差累积产生的,在某一磁极距内不变。

2.3 磁场强度不等

如图3所示,不管是磁栅尺录制原因还是安装原因导致的磁栅尺平面不平,都会使读数头读出的信号的幅值并非处处相等,导致输出信号变为式(4)形式。相当于使用A(x)函数对目标信号进行幅值调制,并且调制信号的频率未知。

Us+=A(x)sinx

(4)

式中A(x)为磁场强度关于位移的函数。

2.4 畸变误差

前述的误差分析中都假设磁栅尺上的磁场为标准的正弦形式,然而实际磁栅尺上的磁场并非是标准的正弦形式,会存在一定的畸变,Us的畸变可用ds(θ)表示,Uc的畸变可用dc(θ)表示。

2.5 误差模型

将式(2)、式(3)、式(4)组合在一起并增加畸变和随机噪声,输出信号变为

Us=A(x)sin[2π(f+δfi)t-δφi+φ1]+ds(x)+

A(x′)sin[2π(f+δfk)t-δφk+φ2]+ns

=Ts(x)sin(θ+φs)+ds(x)+ns+

式中:Ts(x)为信号的幅值波动,Ts(x)=[A(x)cosφ1+A(x′)cosφ2]/cosφs;hk为k/L阶谐波的幅值;φsk为k/L阶谐波的相位;L为整数。

这其中谐波又以三阶谐波为主,因此信号变为

(5)

3 离线参数确定与误差校正

为了使校正算法的计算量最小化,需要尽可能地降低需要实时估计的参数的数量。通过实验可知φs、φc、h3、φs3、φc3参数在全量程范围内基本不变,可以在设备安装后先进行一次离线校正,利用离线校正过程采集的数据估计出以上参数;幅值不等Ts(x)、Tc(x)在整个量程范围内缓慢变化,因此可将离线校正数据的每个最值都保存进查找表中,在实时校正时通过插值获取幅值数据;畸变误差在单周期内随机变化,如果为畸变构建查找表,离线保存的数据量会随精度的提高变得很大,因此畸变误差使用基于频域处理的在线校正方法消除。

3.1 离线参数确定

幅值不等Ts(x)、Tc(x)的查找表MAXs[]、MINs[]、MAXc[]、MINc[], 分别表示每个通道离线采样数据的最值,如图4所示。

图4 幅值不等查找表采样点

φs、φc、h3、φs3、φc3参数需要通过参数估计获得,选择离线采样数据的最大值处构建方程,并假设畸变误差不存在,在Us取最大值时可得到式(6):

(6)

类似地,得到Uc取最大值时的方程:

(7)

通过式(6)、式(7)中的第3个方程,利用二分法可以求解出θ1、θ2的值,以式(8)为评价函数利用梯度下降的方法可得出φs、φc、φs3、φc3以及h3的值,这样所有离线参数都已确定。

(8)

3.2 误差校正

误差校正的流程如图5所示,伪代码如图6所示,进行误差校正的首要步骤是利用CORDIC(coordinate rotation digital computer)算法[13]计算当前采样值所表示的角度,因为CORDIC算法的反正切计算速度比C语言库的计算速度更快,此时可以先不考虑角度误差,因为后续会对角度进行重新计算。

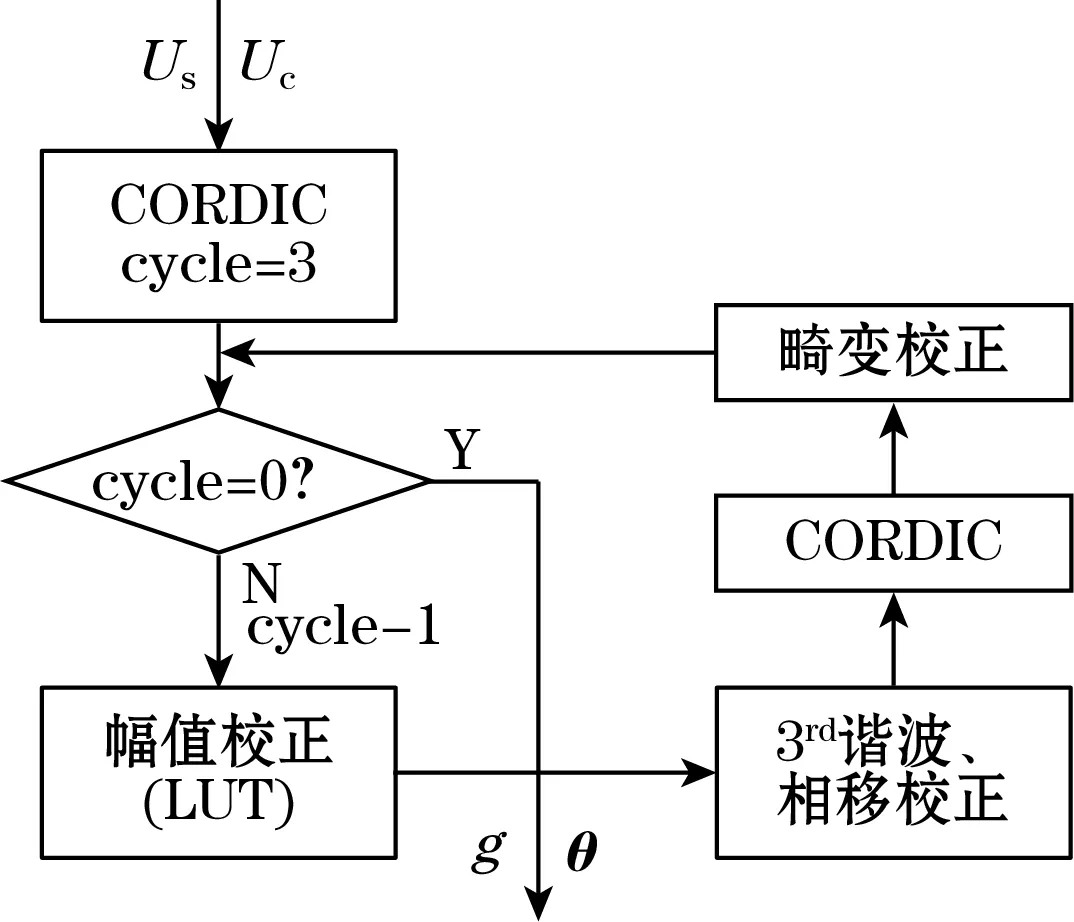
图5 误差校正流程

图6 伪代码

之后进行幅值校正的线性插补[14],因为2个通道的幅值变化不同步,因此插值时只使用本通道的最值数据,Tc的插值计算如下,Ts的计算同理:

在完成幅值不等的校正后需要去除信号中的相移以及三阶谐波,章节3.1已经得到式(5)中的各参数,只需要在采样值中直接减去当前角度值处的三阶谐波值以及相移值即可,如图6中第7、8行所示。

在完成幅值、谐波以及相差校正后,信号变为Us=sinθ+ds(θ),如果此时利用Us-sinθ来获得ds(θ)的值,并在下次循环中减去相应的误差值以期消除畸变,会发现校正后输出信号中的三阶谐波并没有被完全抑制,而且还出现了五阶谐波,这是因为信号中存在的畸变误差影响了开始的角度解算,导致最终的角度没办法收敛到真实值,此时如果在谐波校正后的信号中减去五阶谐波并增加三阶谐波,即可完全消除三阶谐波,如图6中第12,13行所示。

4 实验验证

实验平台结构如图7所示,磁栅尺为SIKO的MB500-1.0-AM-TM-O,磁极距λ=0.01 m,读数头为MS500H,磁栅尺固定在实验平台上,读数头和反射镜跟随丝杆滑块一同运动。使用安捷伦HP5529A激光干涉仪作为位移参考,其线性位移测量分辨率为±1 nm。所提出的算法完全在低功耗MCU ARM-STM32L412KBU6上实现,12 MHz主频下算法的单次运行时间为455 μs,包含模拟信号处理的传感器整体功耗仅13.7 mW,最大的检测速度为10 m/s。

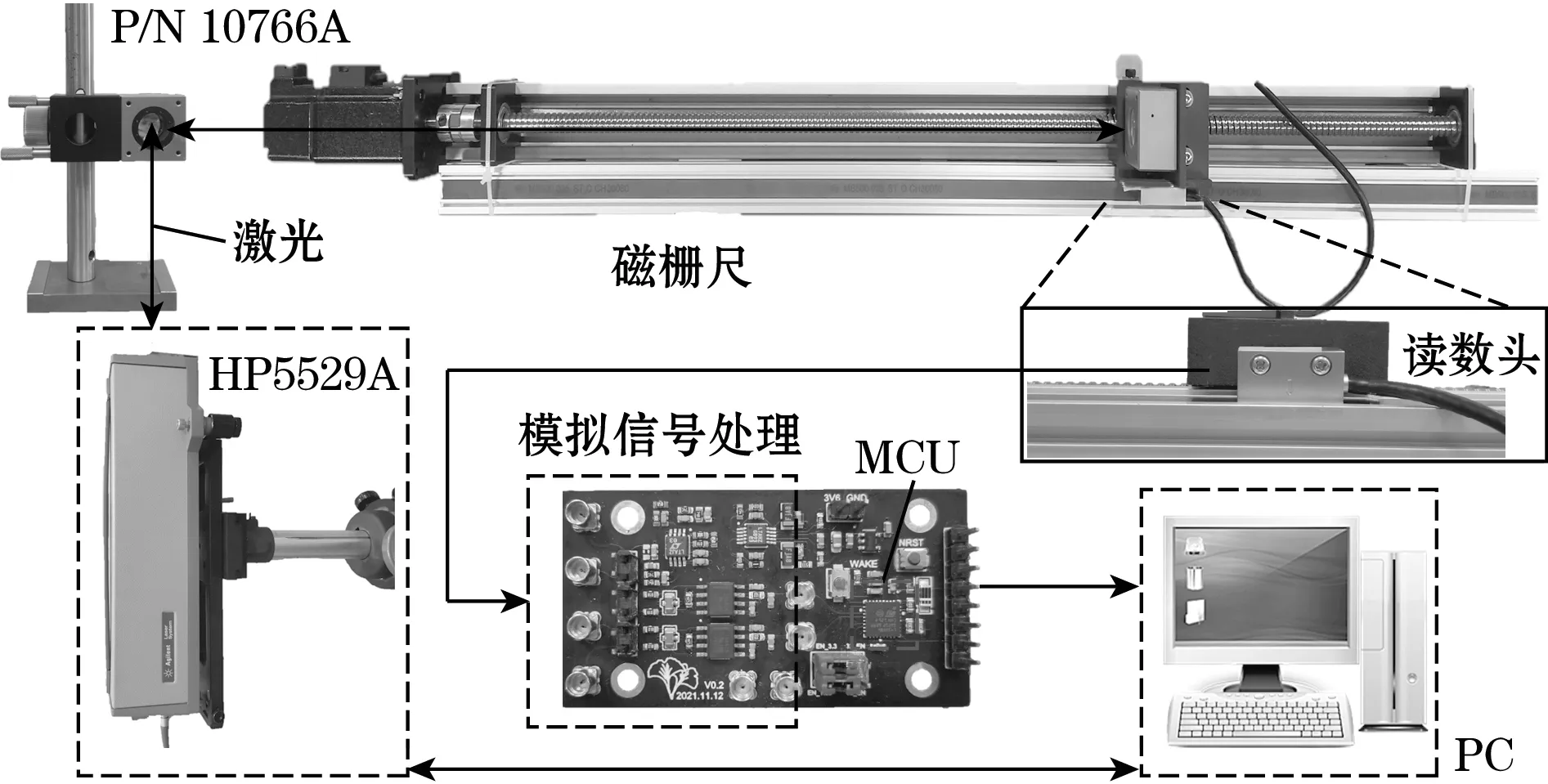
图7 实验平台

实验时读数头按先加速再匀速,再减速到0,然后反向加速、匀速,再减速到0的模式运动,利用PC储存磁编码器以及激光干涉仪输出的数据,并将激光干涉仪的数据作为参考。

图8为角度的解算误差,可以看出在不同阶段算法的性能相同,并不受运动速度的影响。校正前的角度解算精度为±3.95°, 校正后的精度为±0.89°,算法将角度解算精度提升了77.5%,细分倍数由原来的91倍提升为404倍,位移测量精度由±0.109 mm提升为±0.024 7 mm。

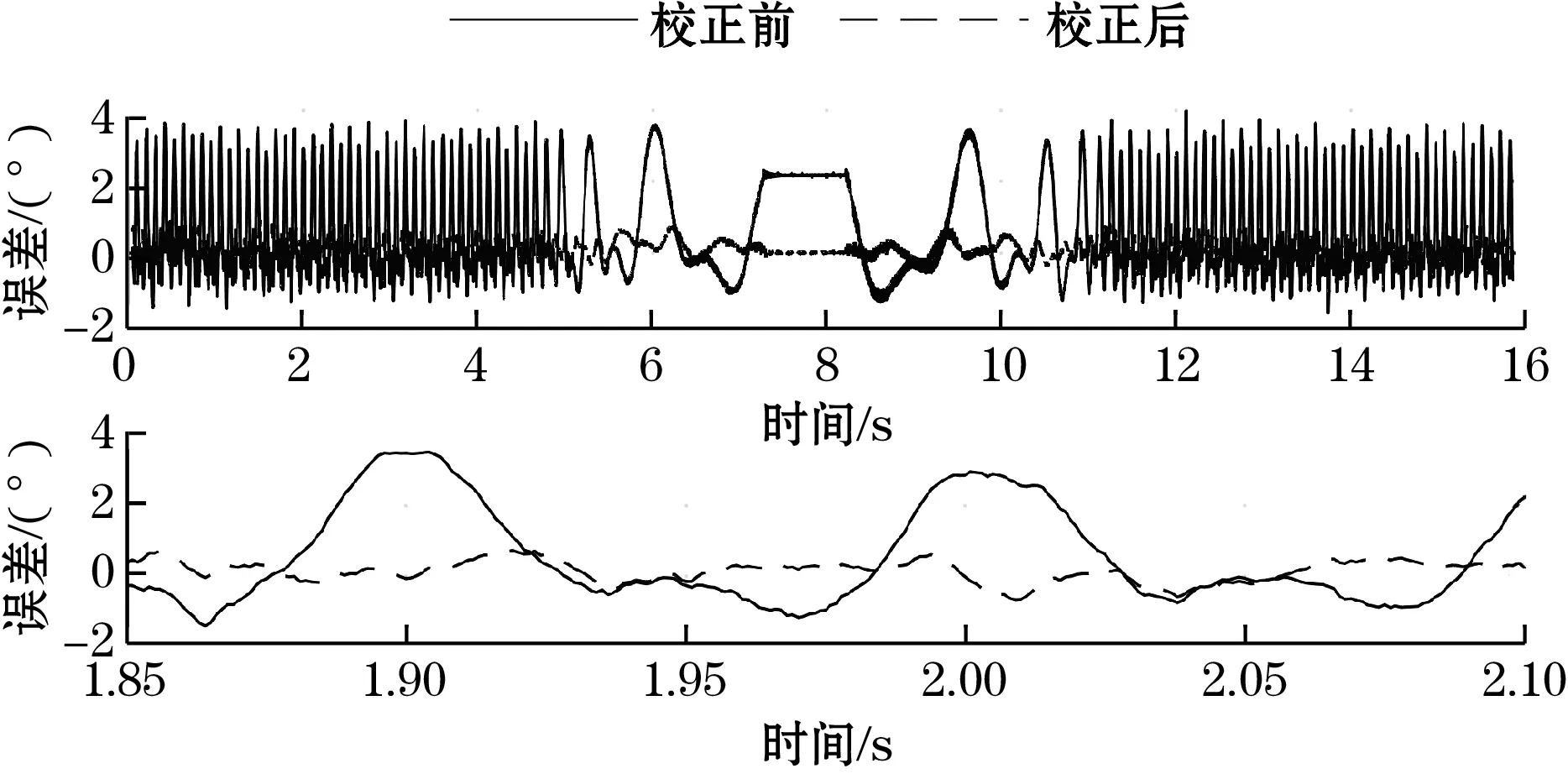
图8 校正前后角度误差

图9为校正后信号的频谱分析结果,可明显看出,校正后信号中的三阶谐波被去除,并且信号中没有引入额外的谐波成分。

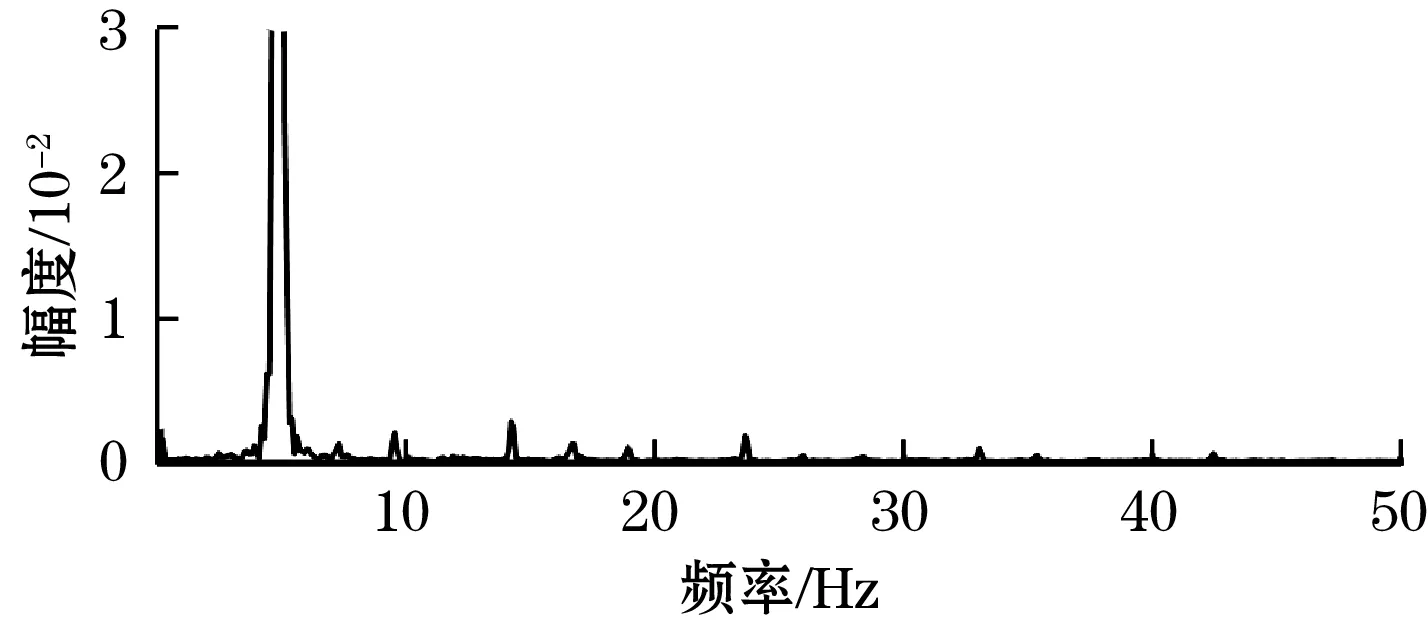
(a)Us校正后频谱局部

图10为校正前后输出信号的lisaru图像与标准lisaru图像的对比,可明显看出校正后输出信号的lisaru图形与标准lisaru图形几乎重合,证明本算法能够有效消除信号中的畸变、谐波等误差。

图10 校准前后的lisaru图形

图11为校正前后的输出信号,可看出校正前的信号中包含幅值不等误差,而信号校正后幅值不等被有效消除。

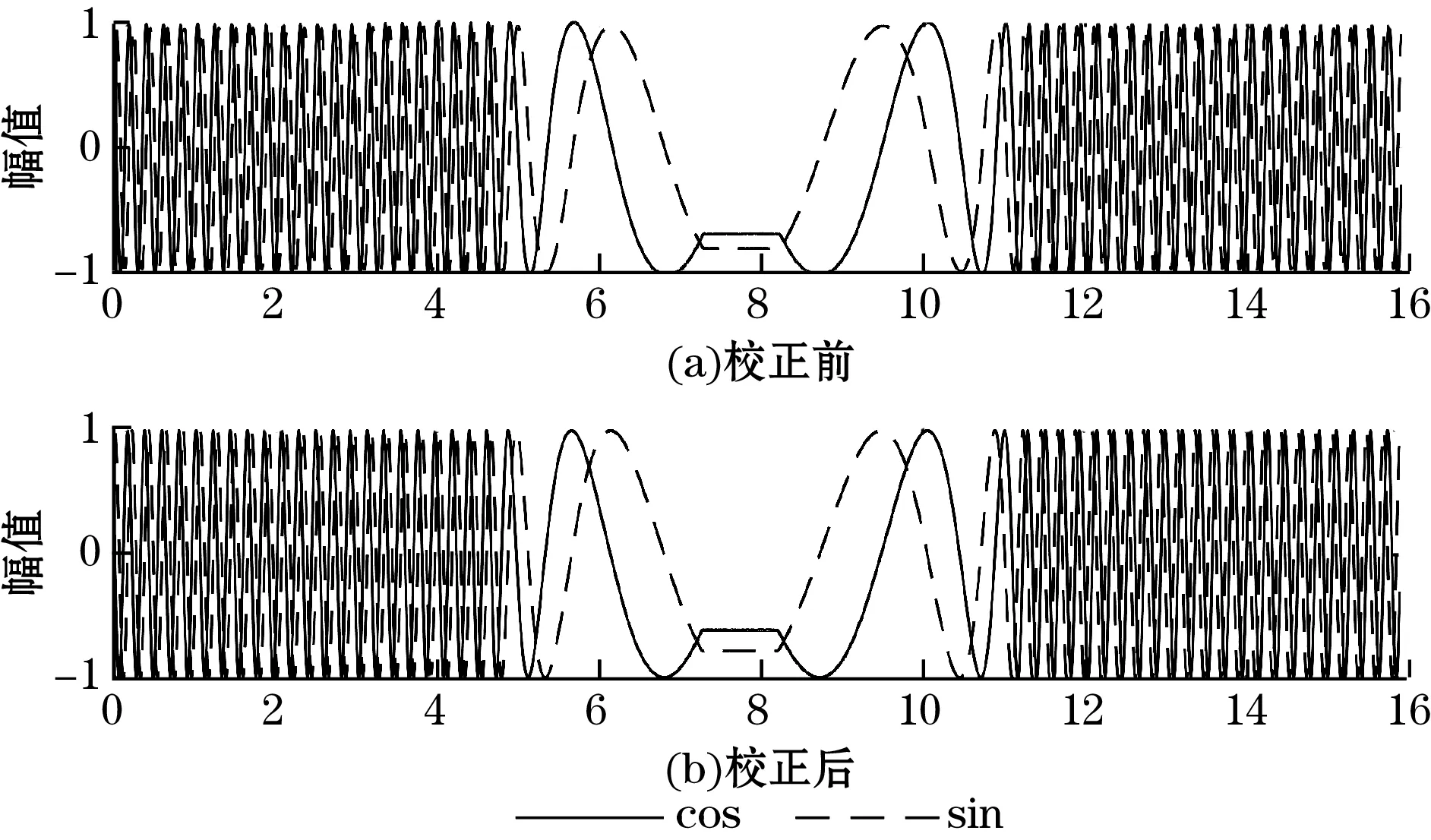
图11 校正前后输出信号

5 结论

本文提出了基于查找表和频域处理的磁栅位移传感器误差校正与细分算法,使用查找表消除磁编码器输出信号中的幅值不等、相移和谐波成分,利用频域处理法消除了信号中的畸变误差。实验表明此算法将位移测量精度提升了77.5%,有效提高了磁栅编码器的细分精度并降低了计算量,使其适用于低功耗、低算力场合。