面向在轨加注的组合体姿态SAC智能控制

郑鹤鸣，翟 光，孙一勇

(北京理工大学宇航学院，北京 100081)

0 引 言

卫星在轨加注技术可以有效延长科学卫星、战略卫星等高价值卫星的在轨运行寿命,从而得到了广泛的关注和研究。美国DARPA提出并执行的“轨道快车”计划[1-2]中,服务星AETRO利用携带的电动泵和高压气瓶作为燃料传输动力,成功向目标星NextSat卫星进行了燃料加注。美国NASA、欧空局还计划建设空间“加油站”,实现实时、高效地对需要燃料补给的卫星进行在轨加注。

在轨加注任务成功的关键在于加注过程中保持服务星和目标星组成的在轨加注组合体的姿态稳定。但是,燃料由服务星向目标星进行传输,导致在轨加注组合体的转动惯量发生实时变化[3]。并且,随着航天技术的发展,卫星呈现大规模化和小型化趋势,大规模的小型卫星在轨加注任务一般使用增压气体对服务星中的加注储箱进行增压驱动液体燃料转移[4]。由于储箱内气液混合,液体燃料会产生晃动,并与质量转移形成复杂的耦合运动,从而给姿态带来随机扰动,甚至会导致任务失败[5]。Lee等[6]利用计算流体力学(CFD)数值仿真的方法研究了微重力环境下储箱内部燃料质量变化时的液体运动规律。文献[7-8]利用弹簧阻尼模型和球形单摆模型模拟了卫星储箱中的液体燃料运动。目前,针对在轨加注过程中复杂液体运动的动力学建模还不够充分,使得姿态控制器的设计缺乏依据。

已有很多研究提出了针对具有转动惯量时变特点的卫星的姿态控制方法[9-11]。但是,在轨运行过程中,同一个服务星需要连续且高效地对多颗质量、转动惯量、储箱结构等参数不同的目标星进行加注。并且,目标星的这些关键参数可能是未知或无法进行精确测量的,这也导致无法对储箱中液体燃料的运动进行预测。在轨加注组合体是结构参数可变、未知且具有随机性的系统,文献[9-11]提出的经典控制方法很难针对这些特点有效地控制在轨加注组合体的姿态。基于深度强化学习方法的智能控制器通过不断和控制环境进行交互,根据对环境状态的测量和系统反馈的奖励值更新策略,最终达到理想的控制效果[12-13]。该方法不依赖于系统的模型,可以有效应对在轨加注组合体系统参数未知且随机变化的特点。深度强化学习方法在航空航天领域的导弹制导[14-15]、飞行器姿态控制[16]、深空探测器自主导航[17]、航天器机械臂路径规划[18]等领域得到了广泛的应用。

深度强化学习算法之一的SAC算法基于随机性策略,并通过引入信息熵来提高策略寻优的鲁棒性。该算法能够有效应对加注过程中由液体晃动-转移耦合运动引起的姿态随机扰动,弥补传统控制方法在此方面的不足。SAC算法的有效性已在一些自动化系统的应用中得到了验证。文献[19]基于SAC算法开发了无人机自主空战策略,实现无人机自主分析空战态势,率先锁定并攻击敌方目标。针对工作区域内的复杂地形环境,文献[20]提出了一种基于SAC算法的多臂机器人自主路径规划方法,实现机器人自主躲避工作区域中固定和移动的障碍物。文献[21]针对海洋环境存在无法建模的复杂外扰动的特点,应用SAC算法设计了自动水下潜艇的导航和控制方法。上述文献中,空战、障碍工作区和水下的背景环境均具有强随机性的特点,而SAC算法均采用了有效的策略克服了环境的随机性,达到了预期效果。

本文通过对SAC算法进行改进提出了在轨加注组合体的姿态智能控制方法。主要创新点有:构建了液体燃料晃动-转移耦合运动的等效模型和在轨加注组合体变惯量姿态动力学环境,与智能控制器进行交互训练。改进了SAC算法的动作输出方式,基于此设计的SAC姿态智能控制器,相较于TD3算法,在应对时变系统的随机扰动时鲁棒性较强。提出的SAC加注压强智能控制器在保证加注效率的同时,通过调节加注压强,减缓加注对姿态产生的扰动作用,使姿态的收敛更加平稳。

1 在轨加注组合体变惯量姿态动力学

智能控制器需要通过大量的训练来得到最优的控制策略。为了提高效率和可操作性并降低成本,智能控制器的训练在仿真环境中进行。训练完成后,将训练好的智能控制策略部署到真实的在轨加注服务星的星载计算机中并在实际任务中应用。为了保证智能控制器在实际任务中实现理想的控制效果,在仿真系统中对智能控制器进行训练时,要建立并采用高精度的姿态动力学环境。

在轨加注组合体的结构模型如图1所示。假设服务星和目标星各携带一个和卫星平台固连的燃料储箱;卫星对接后两个储箱的轴向重合。

图1 在轨加注组合体示意图

分别建立地球惯性坐标系、轨道坐标系和本体坐标系。Oxyz代表的地球惯性坐标系是一个原点固连在地球质心、无旋转的坐标系。Oxoyozo代表的轨道坐标系,其原点位于在轨加注组合体结构平台的质心,Oxo轴与轨道速度矢量重合,Ozo轴与从组合体质心指向地球质心的矢量重合。Oyo轴符合右手定则。本体坐标系由Oxbybzb表示,原点位于组合体结构平台质心,Oxb轴与储箱轴向重合并指向目标星,Oyb轴平行于主对称平面并垂直于Oxb轴,而Ozb轴符合右手定则。

服务星通过对加注储箱进行加压驱动液体燃料向受注储箱转移,在达到预定的加注质量后停止加压。将服务星对加注储箱内施加的加注压强表示为

(1)

式中:Pc为加注过程中加压控制装置输出的加注压强;mt和maim分别为转移液体的质量和加注的目标质量。液体的质量流率与加注压强的关系可以表示为[3]

(2)

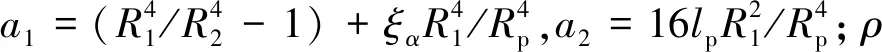
(3)

加注过程中,储箱中的液体燃料会分散成液滴,分散的液滴会发生晃动,并与质量转移形成复杂的耦合运动,从而给在轨加注组合体的惯量带来随机的变化。通过确定液体燃料相对自身惯量主轴的惯量和质心的运动来衡量液体燃料晃动-转移耦合运动对在轨加注组合体整体的影响。文献[5]中提出了在轨加注过程中储箱内液体燃料晃动-转移耦合运动的等效动力学模型,并通过与CFD模型进行仿真对比,验证了该等效模型能够精确地模拟在轨加注过程中形状复杂的燃料液滴的惯量变化和整体质心运动。对于分散液滴的惯量采用等效椭圆柱模型来进行描述。将第i(i=1,2)个储箱中液体相对自身惯量主轴的转动惯量表示为一个等效椭圆柱的惯量[5]：

(4)

式中:mi是任意时刻储箱中液体燃料的质量;li,ai,bi分别是液体等效椭圆柱的三个特征长度,特征长度的值及导数通过下式确定:

(5)

式中:lsi为液体燃料不发生晃动时的特征长度[5]。

第i个(i=1,2)储箱中液体相对自身惯量主轴的转动惯量的导数为

(6)

第i个储箱中液体燃料的质心在本体坐标系内的位置和速度可以表示为

(7)

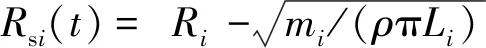
(8)

式中:ω=[ωx,ωy,ωz]T为惯性坐标系下组合体绝对姿态角速度。

在轨加注组合体相对于自身惯量主轴的惯量由刚性平台和液体惯量两部分构成。储箱内液体晃动-转移耦合运动通过式(4)至式(8)所描述的液体自身转动惯量的变化和质心的运动来影响在轨加注组合体整体的惯量变化。将在轨加注组合体的转动惯量表示为[3]

(9)

式中:Jl(t)为液体燃料相对于在轨加注组合体惯量主轴的转动惯量;E代表3×3的单位矩阵。将在轨加注组合体转动惯量的时间导数表示为

(10)

将在轨加注组合体的变惯量姿态动力学表示为

(11)

式中:ω×为ω的反对称叉乘矩阵。将x=[x1,x2,x3]T的反对称叉乘矩阵定义为

(12)

采用姿态四元数Qatt=[q0,q]T=[q0,q1,q2,q3]T描述在轨加注组合体的姿态运动学。姿态四元数方法通过使本体坐标系绕一固定轴η旋转一定角度ξ与轨道坐标系重合来表示本体坐标系相对于轨道坐标系的姿态,姿态四元数可以表示为

(13)

将基于姿态四元数的姿态运动学的微分方程表示为

(14)

式中:ωb为本体坐标系相对于轨道坐标系的姿态角速度,满足:

ωb=ω-Tbo(Qatt)ωo

(15)

式中:ωo为组合体的轨道角速度;Tbo(Qatt)为姿态四元数表示的姿态转换矩阵:

Tbo(Qatt)=

(16)

2 改进的深度强化学习SAC算法

2.1 在轨加注组合体的强化学习智能控制系统

在轨加注组合体的深度强化学习控制包含智能控制器(agent)和动力学环境(environment)两个部分,基本结构如图2所示。智能控制器具有学习和决策的能力。动力学环境就是上一节中由式(11)和式(14)确定的在轨加注组合体变惯量姿态动力学。

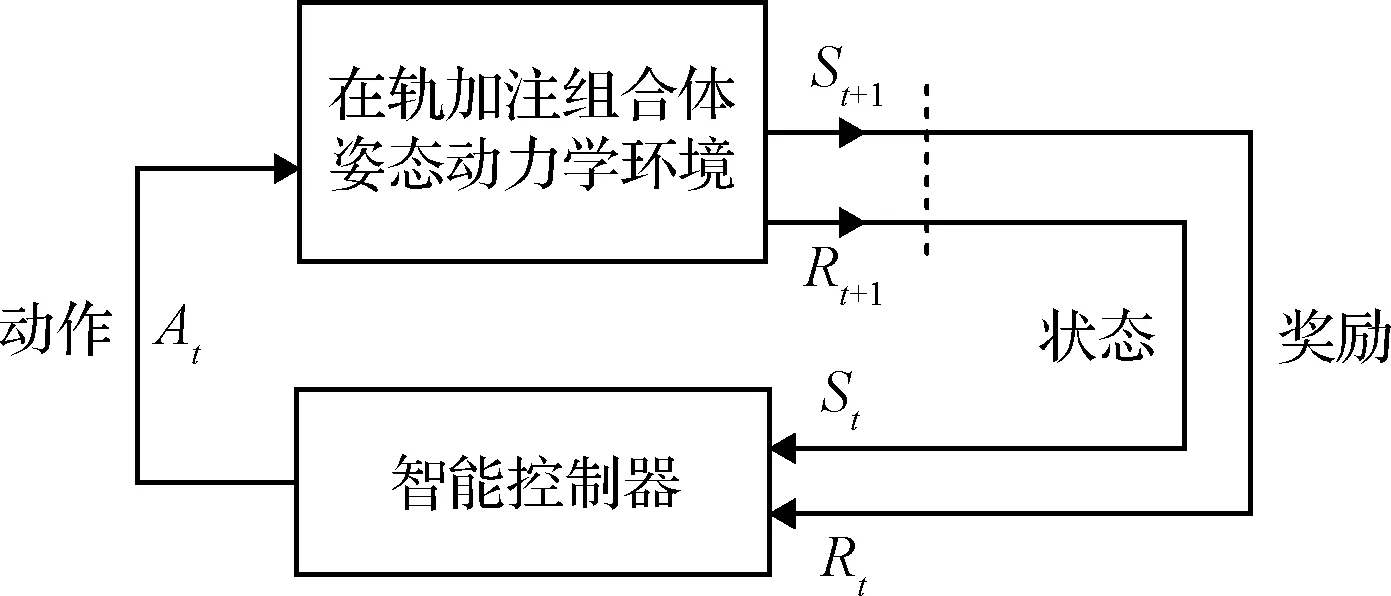
图2 在轨加注组合体的强化学习智能控制系统

智能控制器通过和动力学环境的不断交互从而对控制策略进行学习,最终得到实现控制目标的最优控制策略,这个过程就是对智能控制器的训练。训练的过程采用马尔科夫决策过程(MDP)进行描述[12]。MDP通常由一个四元组构成,表示为:,其中,S表示环境状态的集合,A表示智能控制器动作的集合,P为环境的状态转移概率,而R表示奖励函数。在训练过程中的任意t时刻,智能控制器感知环境的状态St∈S,并通过一个动作At∈A,使环境按照概率P转移到下一个状态St+1∈S,并得到环境的一个潜在奖励Rt。

(17)

式中:γ∈[0, 1]为折扣因子。

智能控制器中评估的功能就是通过对当前策略能够获得的长期累积奖励进行估计从而评价当前策略的质量并对策略进行更新。深度强化学习在强化学习的基础上利用两个命名为Actor和Critic的神经网络分别代替智能控制器中的策略和评价,这种方法也称为Actor-Critic算法。两个神经网络均由输入层、一个及以上的隐含层和输出层构成。Actor网络输入层的输入是环境的状态,通过隐含层的拟合,输出层输出的是策略;对于确定性算法,网络将直接给出动作的值;对于随机性策略,Actor将输出一个概率分布,再根据概率分布采样得到动作。Critic网络输入层的输入是环境的状态以及动作执行后获得的奖励值,输出层输出的是通过隐含层拟合得到的Q函数的值。Actor网络和Critic网络的参数分别用φ,θ表示。

2.2 改进的SAC算法

SAC算法是深度强化学习中的一种基于随机性策略的算法,它的基本原理是在智能控制器训练的过程中,希望长期的累加奖励值和策略的信息熵都达到最大,也称为最大熵强化学习[13]。该算法长期累加奖励的表达式为

(18)

式中:H(Π(·|St))为策略的信息熵,定义为策略中所有动作的平均不确定性:

H(Π(·|St))=E(-lgP(At|St))=

(19)

动作的产生是一个信息熵减的过程,所以信息熵为负值。通过最大化策略的信息熵,增加策略的随机性,使每个动作产生的概率尽可能分散,而不是集中于一个动作,从而增强训练过程中策略的探索并提高控制的鲁棒性。α为熵权重系数。

SAC智能控制器中Critic神经网络的代价函数为[13]

(20)

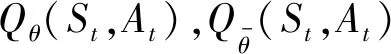
(21)

式中:DKL(X|Y) 代表KL散度函数,Qsoft(St,At)为Critic神经网络的柔性贝尔曼方程(Soft Bellman equation)。

在SAC智能控制器的训练过程中,由于奖励值在不断变化,固定的熵权重系数会导致训练过程不稳定,所以需要对熵权重系数进行实时调节。熵权重系数的调节基于优化的思想,设置代价函数,并通过梯度下降法求解最优值。熵权重系数调节过程中使用的代价函数为

Jα(θ)=EAt+1～Πφ(-αlgΠφ(At|St)-αH0)

(22)

SAC算法的流程如图3所示。

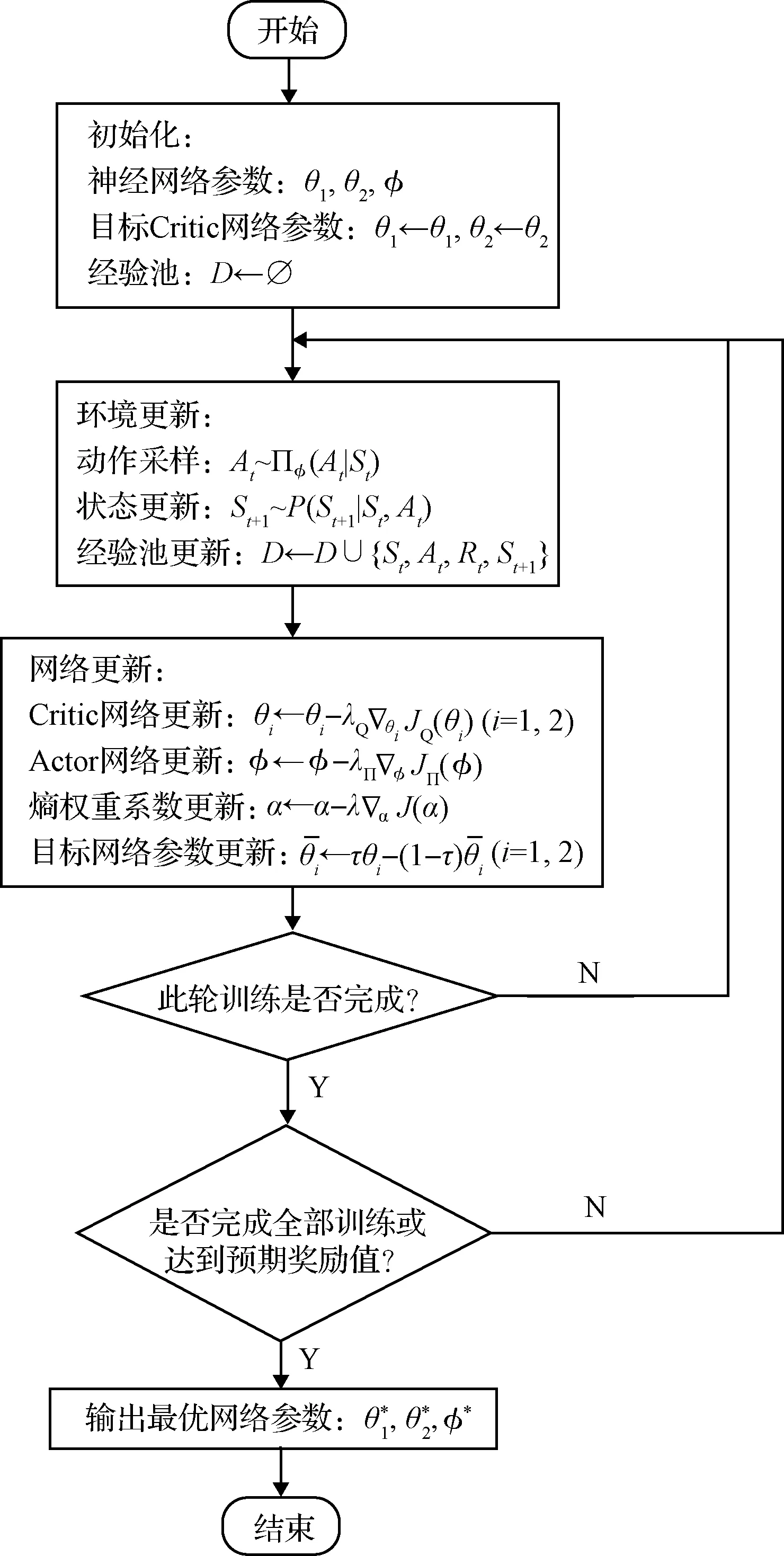
图3 SAC算法流程图

本文针对在轨加注组合体姿态具有随机扰动的特点,对SAC算法输出动作的方式进行了改进。在训练过程中,SAC算法输出的是一个代表策略的高斯分布Πφ～N(μ,δ)的均值μt和方差δt,智能控制器通过高斯分布进行采样输出动作,具体采样方式如下所示:

At=μt+rand(0,1)δt

(23)

式中:rand(0,1)代表0到1之间的随机数。训练时输出的动作具有随机性,这样可以使策略快速适应系统中的随机扰动,从而提高策略寻优的效率。但是,在实际任务中,随机的控制输出会给执行机构带来很大的负担,甚至无法达到控制目的。所以将智能控制器部署到服务星星载计算机时,将智能控制器的输出进行改进,消除由概率分布方差引起的随机项。改进后的控制力矩输出为

(24)

实际任务中,根据式(24)输出确定性的控制指令,可以有效提高控制的稳定性。

3 SAC姿态和加注压强智能控制器设计

基于上述改进的SAC算法进行智能控制器的设计。首先,为了能够在加注过程中保持卫星组合体姿态的稳定,需要对姿态智能控制器进行设计和训练。然后,姿态扰动的惯量变化是加注过程中液体质量重新分布导致的;由式(2)和式(3)不难发现,加注压强直接决定液体的质量流率,很大程度上影响了液体质量的重新分布过程。对加注压强进行控制,可以调节液体的质量流率,从而减小随机扰动对姿态的影响;所以在训练并部署好姿态智能控制器的基础上,对加注压强智能控制器进行设计和训练。

3.1 SAC姿态智能控制器设计

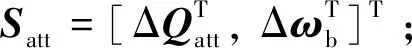
(25)

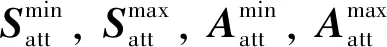
将SAC姿态智能控制器的奖励函数设计为

(26)

式中:

(27)

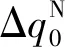
SAC姿态智能控制器中,两个Critic网络具有相同的结构,每个网络首先分别有状态路径和动作路径两条支路,每条支路具有若干个隐含层,两个支路通过一条具有若干个隐含层的公共路径连接,并最终输出Q值。Actor网络首先有一条具有若干隐含层的公共路径,然后分出两条具有若干隐含层的支路分别来拟合策略概率分布的均值和方差。

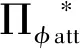
(28)

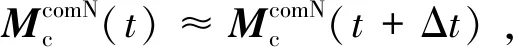
(29)

由式(14)和式(29),易得:

(30)

设组合体姿态的状态向量为

(31)

选取李雅普诺夫函数:

(32)

对李雅普诺夫函数求导,并根据式(30),能够得到:

(33)

所以组合体姿态具有稳定性。

3.2 SAC加注压强智能控制器设计

在完成对姿态智能控制器的训练后,将训练好的SAC姿态智能控制器部署到闭环的控制系统中,再对SAC加注压强智能控制器进行设计和训练。

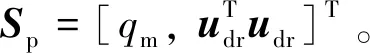
(34)

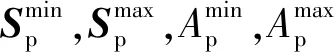
将SAC加注压强智能控制器的奖励函数设计为

(35)

式中:

(36)

奖励函数分为状态相关的奖励值和惩罚项两部分。由于希望更高效地完成加注任务,需要液体的质量流率尽量大,所以赋予质量流率以正值的权重;同时希望随机扰动尽量小,所以赋予加注压强模的平方以负值的权重;由于减小随机扰动的优先级大于高效完成加注任务,所以质量流率权重的绝对值小于随机扰动模的平方值权重的绝对值;同时赋予时间和任务结束时间的比值以负值奖励,同样是为了促进高效的加注。惩罚项中,Ptri为加注管理系统给加压系统的开关机信号,当其值为0时,加压机构根据指令加注压强进行加压,其值为1时,加压机构关机结束加注。当任务结束时如果还未结束加注,则说明加注未能成功完成,给出较大的惩罚值。当加注结束或达到任务结束时间,自动退出此轮训练。

SAC加注压强智能控制器中Actor和Critic网络的结构与SAC姿态智能控制器中的神经网络结构保持一致。基于SAC加注压强智能控制给出:

定理 2.当SAC加注压强智能控制器的策略得到最优解Πφp*,则加注扰动和加注总时间均有界且最小。

证.若SAC姿态智能控制器的策略得到最优解Πφp*,则采用Πφp*时,奖励值随着时间增加且奖励值总和最大,即:

(37)

(38)

即加注扰动有界且最小。

ttot→min

(39)

即总加注时间ttot有界且最小。

4 仿真分析

根据上述变惯量姿态动力学模型和设计的智能控制器,在仿真环境中建立在轨加注组合体姿态智能控制系统。首先对SAC姿态智能控制器进行训练,并通过仿真算例验证了SAC姿态智能控制器部署到实际加注任务中的有效性。通过与TD3算法进行对比,验证了改进的SAC算法的优势。然后在部署好SAC姿态智能控制器的条件下,对SAC加注压强智能控制器进行训练,验证了SAC加注压强智能控制对姿态控制效果的改善。

仿真算例中,根据目前的小型卫星试验平台设计了组合体相关参数[5],可为将来针对小型化卫星在轨加注技术的空间试验验证提供仿真参考。在所有仿真算例中,任务的时间均设置为tf=300 s,时间步长设置为ts=0.1 s;假设在轨加注组合体运行在轨道高度h=400 km的圆形地球轨道上且加注的液体燃料为偏二甲肼,密度为ρ=1 011 kg/m3。

4.1 SAC姿态智能控制器训练和部署仿真

首先,对SAC姿态智能控制器进行训练,并对训练的效果进行分析。训练时选取的组合体参数要尽量与任务中实际的组合体参数接近或保持同一量级。在该算例中,在轨加注组合体的相关参数见表1。

表1 姿态智能控制器训练算例在轨加注组合体参数

SAC姿态智能控制器中Actor和Critic网络的具体参数如图4所示。两个Critic网络中,状态路径和动作路径两条支路各具有两个隐含层,每个隐含层具有64个神经元,两个支路通过一个具有64个神经元的公共隐含层连接。Actor网络具有一个64个神经元的公共隐含层,均值路径和方差路径两条支路各具有一个64个神经元的隐含层和一个输出层。

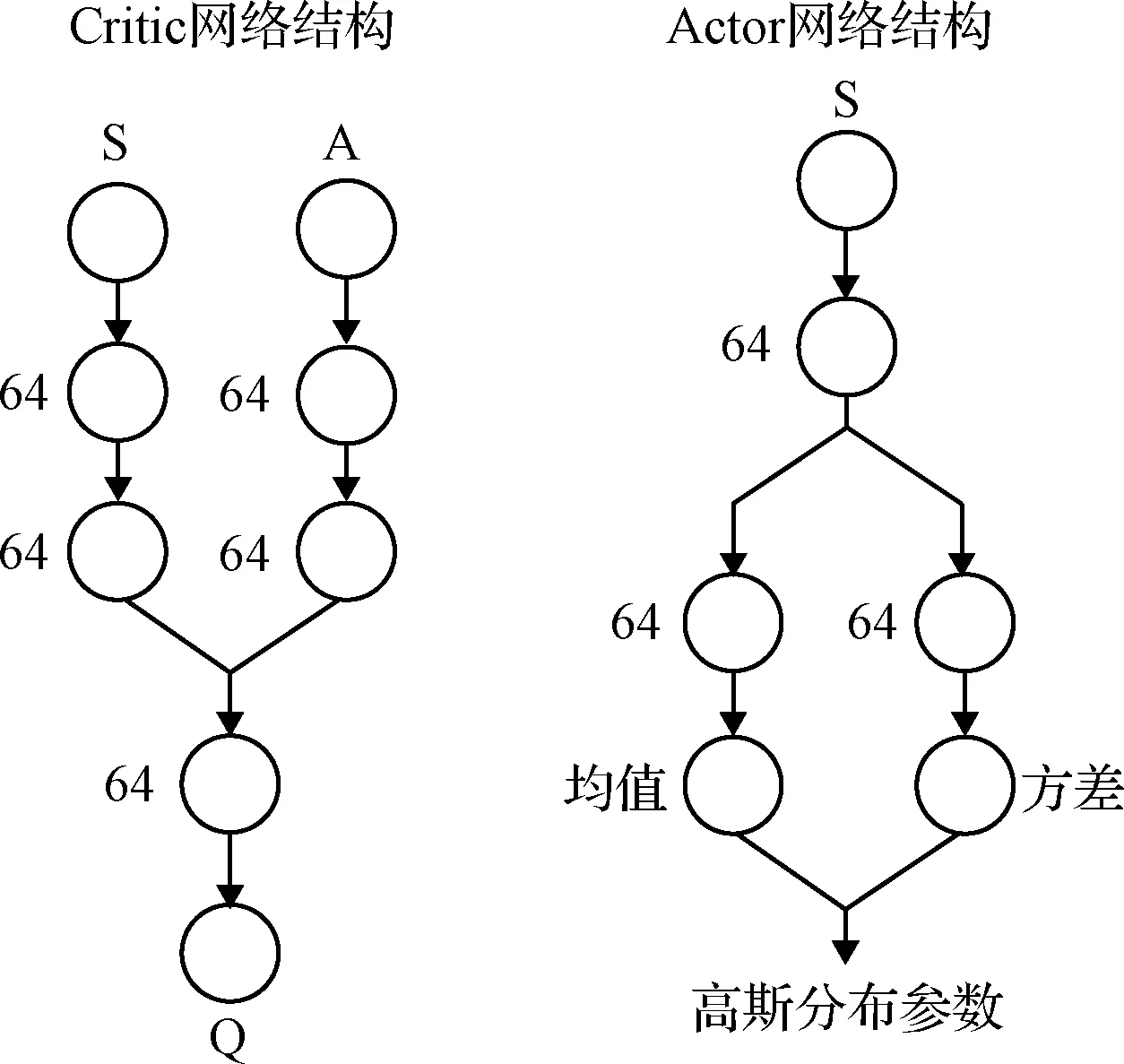
图4 SAC姿态智能控制器神经网络参数示意图

SAC姿态智能控制器的关键训练参数见表2。

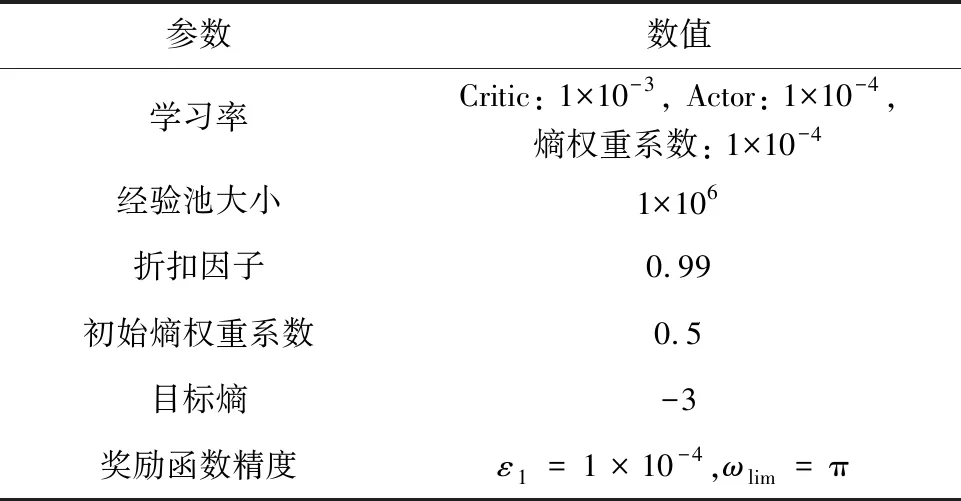
表2 SAC姿态智能控制器的关键训练参数

为了验证基于随机性策略的SAC算法在控制在轨加注组合体姿态方面的优势,利用深度强化学习方法中基于确定性策略的TD3算法[22]作为对比。TD3算法采用延迟学习的思想,使两个Critic网络的更新频率比Actor网络的更新频率要大,促进评估和策略的稳定收敛。并且基于确定性策略:At=Π(St|θπ),训练过程中对Actor网络给出的动作加入噪声,从而促进探索。

基于TD3算法设计了姿态智能控制器,用于与SAC姿态智能控制器对比。两个姿态智能控制器具有相同的输入输出参数和奖励函数。TD3姿态智能控制器中Actor和Critic网络的结构和参数如图5所示。两个Critic网络与SAC姿态智能控制器中的Critic网络结构相同。Actor网络较为简单,通过两个具有64个神经元的隐含层来给出确定性的动作。

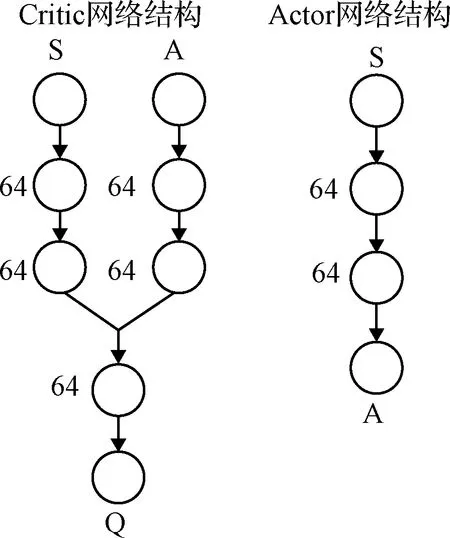
图5 TD3姿态智能控制器神经网络参数示意图

TD3姿态智能控制器的关键训练参数见表3。

表3 TD3姿态智能控制器的关键训练参数

对两个姿态智能控制器进行训练,训练过程中两个姿态智能控制器获得的奖励值曲线如图6所示。两个姿态智能控制器均经历了150轮训练。初始时,SAC姿态智能控制器的奖励值从-2 150快速攀升。由于SAC算法的决策具有随机性,会不断尝试不同的策略,奖励值在训练中途产生了大幅下降,这是SAC算法不断试错的结果。在尝试出现错误后,SAC算法也能够快速纠错。奖励值在4轮训练下降后迅速回升,说明已经找到策略更新最优的方向。最终,奖励值于第70轮训练平稳收敛到-50。TD3姿态智能控制器的初始得分为-1 200,在经历120轮训练的波动攀升后,奖励值平稳收敛到-80。在训练的过程中,SAC算法奖励值变化的范围和幅度比TD3算法都大,说明SAC算法对策略的尝试更多,基于SAC算法的随机性策略比基于TD3算法的确定性策略对环境的探索范围更大。所以SAC算法奖励值的收敛也就更快,训练寻优的效率也就更高。同时SAC算法收敛后的奖励值也比TD3算法高,这说明SAC姿态智能控制器具有更好的控制效果。

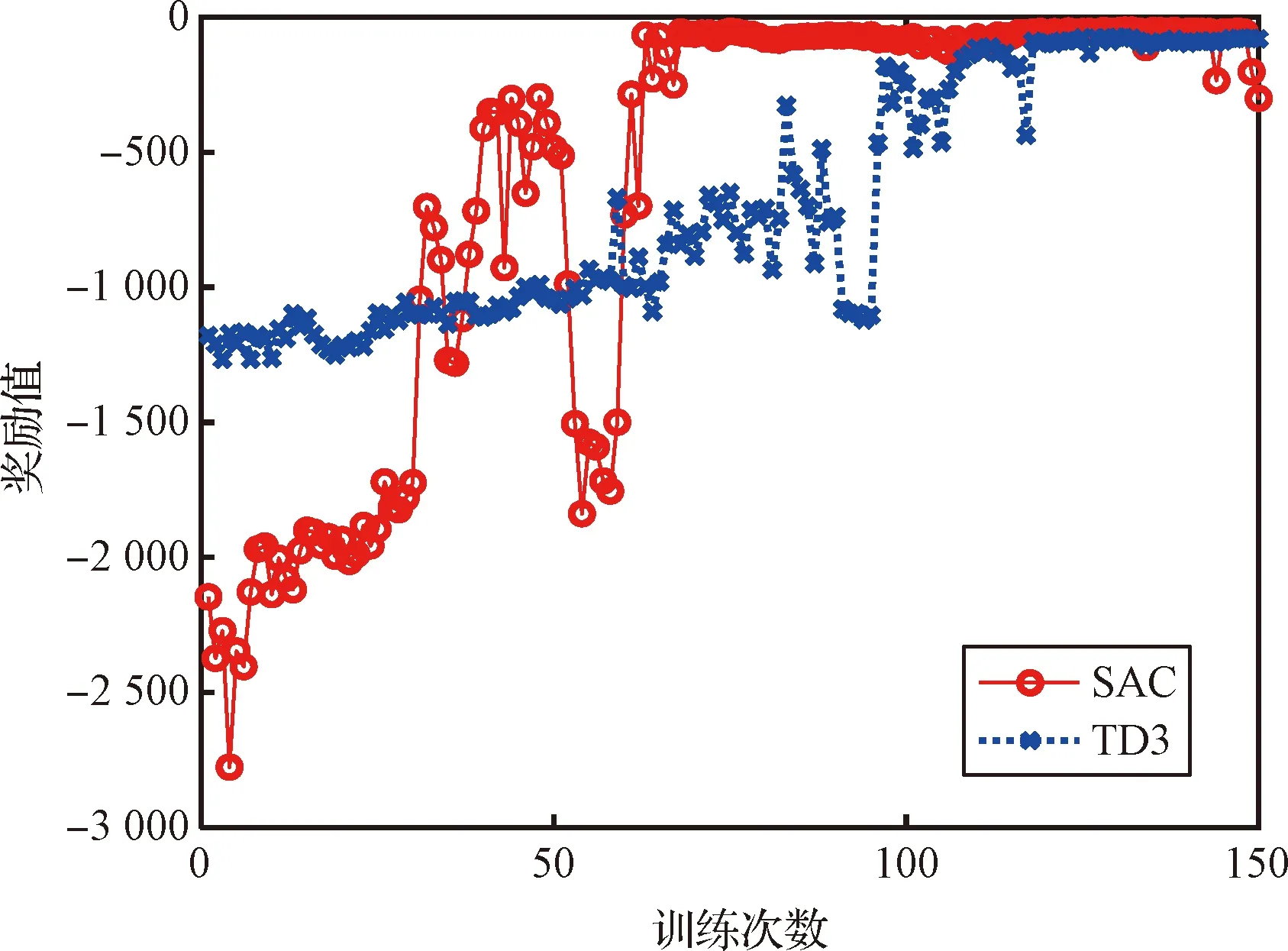
图6 姿态智能控制器训练奖励值曲线

图7所示的是训练完成的SAC姿态智能控制器输出的控制力矩。该控制力矩在三轴均产生高频且高幅的振动现象。根据式(23),这种现象的发生是因为训练过程中姿态智能控制器输出的是通过概率分布采样得到的随机控制力矩,这可以有效增加寻优效率,但该随机的控制信号无法直接输入到实际的执行机构中。

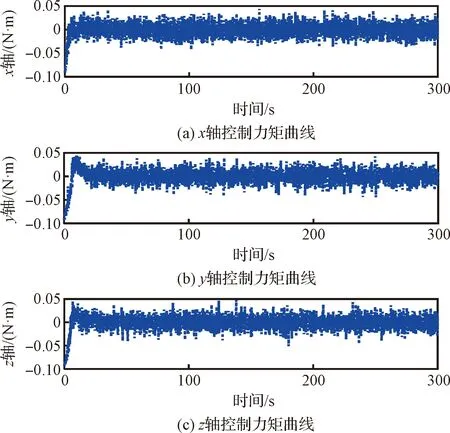
图7 训练后SAC控制力矩曲线

实际任务中,将SAC姿态智能控制器部署到服务星,连续对一系列目标星进行加注。这些目标星的结构参数存在未知的差异,且转移燃料质量的加注需求也不尽相同。在该仿真算例中,对组合体参数做出调整,以模拟实际中同一任务的目标星与训练中的目标星可能存在的最大差异,从而验证SAC姿态智能控制器部署后的鲁棒性。将在轨加注组合体平台惯量修改为Jr=diag(10,10,10) kg·m2,目标星中储箱尺寸修改为L2=0.4 m,R2=0.1 m,目标填充率修改为50%。同时,由于液体晃动-转移耦合运动存在未建模的模态,等效模型和液体真实运动之间存在细微的差距,真实的液体运动对姿态会产生复杂的随机扰动,随机扰动产生影响的直接体现就是真实的在轨加注组合体惯量产生随机的变化。为了模拟实际任务中在轨加注组合体惯量真实的随机变化,在式(9)的基础上引入一个正弦形式变化的惯量随机项:

Jreal(t)=J(t)+0.5rand(0,1)·

sin(0.02πt)1(3,3)

(40)

式中:1(3,3)为元素全为1的3×3矩阵。初始姿态改变为:姿态角Φ=[30°, 30°, 30°]T,姿态角速度ωb=[0.1, 0.1, 0.1]Trad/s。

利用上述参数设置进行仿真,两个姿态智能控制器输出的控制力矩、在轨加注组合体的姿态角速度和姿态角的控制效果分别如图8～10所示。根据式(24)改进动作输出方式后,SAC姿态智能控制器输出的三轴控制力矩没有出现高频高幅的振动现象,且最大幅值为0.1 N·m,说明改进后的SAC姿态智能控制器可以有效部署到实际的任务中。TD3算法输出三轴控制力矩的最大幅值为0.3 N·m,是SAC姿态智能控制器输出控制力矩最大幅值的3倍。且TD3算法输出的控制力矩在收敛前出现了高频高幅的震动现象,SAC姿态智能控制器输出的控制力矩并没有出现此现象。相应地,TD3算法控制的姿态角速度的波动次数、频率和幅值均高于SAC姿态智能控制器控制的姿态角速度。姿态角控制效果方面,为了直观展示姿态的变化,将姿态四元数转化为三轴的姿态角:滚转角、俯仰角和偏航角。TD3算法控制的三轴姿态角最大幅值为73°,小于SAC姿态智能控制器的88°;但是TD3算法控制的三轴姿态角的收敛过程相较于SAC姿态智能控制器仍产生了更多的波动,不如SAC姿态智能控制器的控制效果平稳。综上,两个姿态控制器虽然均能实现姿态稳定控制;但相较于TD3算法,SAC姿态智能控制器可以实现利用更小幅值和更稳定的控制力矩使在轨加注组合体的姿态更加平稳地收敛,证明了SAC姿态智能控制器部署到实际的在轨加注任务后,应对结构参数和加注需求完全不同的目标星时,能够实现姿态控制的鲁棒性要求。

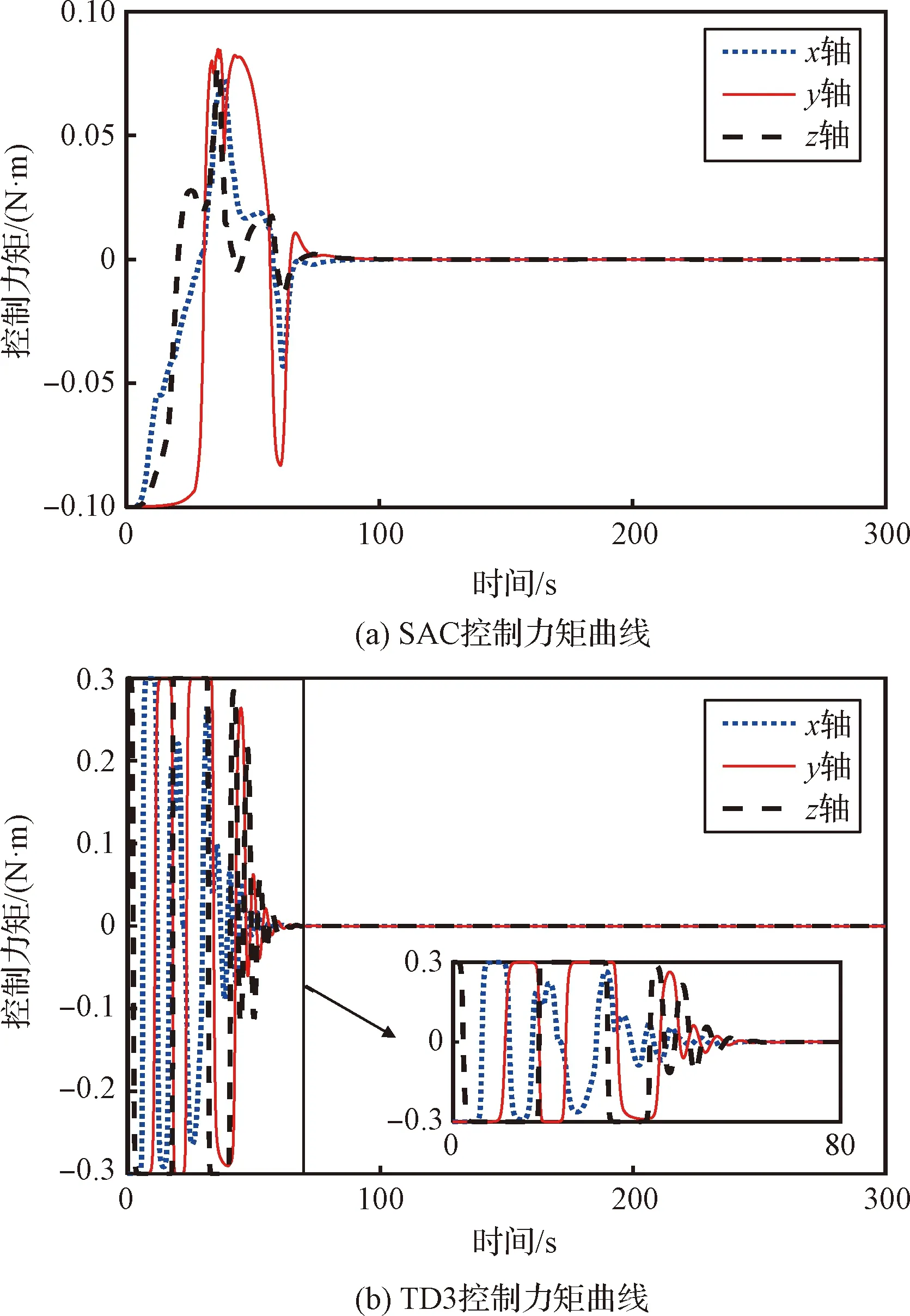
图8 姿态智能控制器部署后的控制力矩曲线

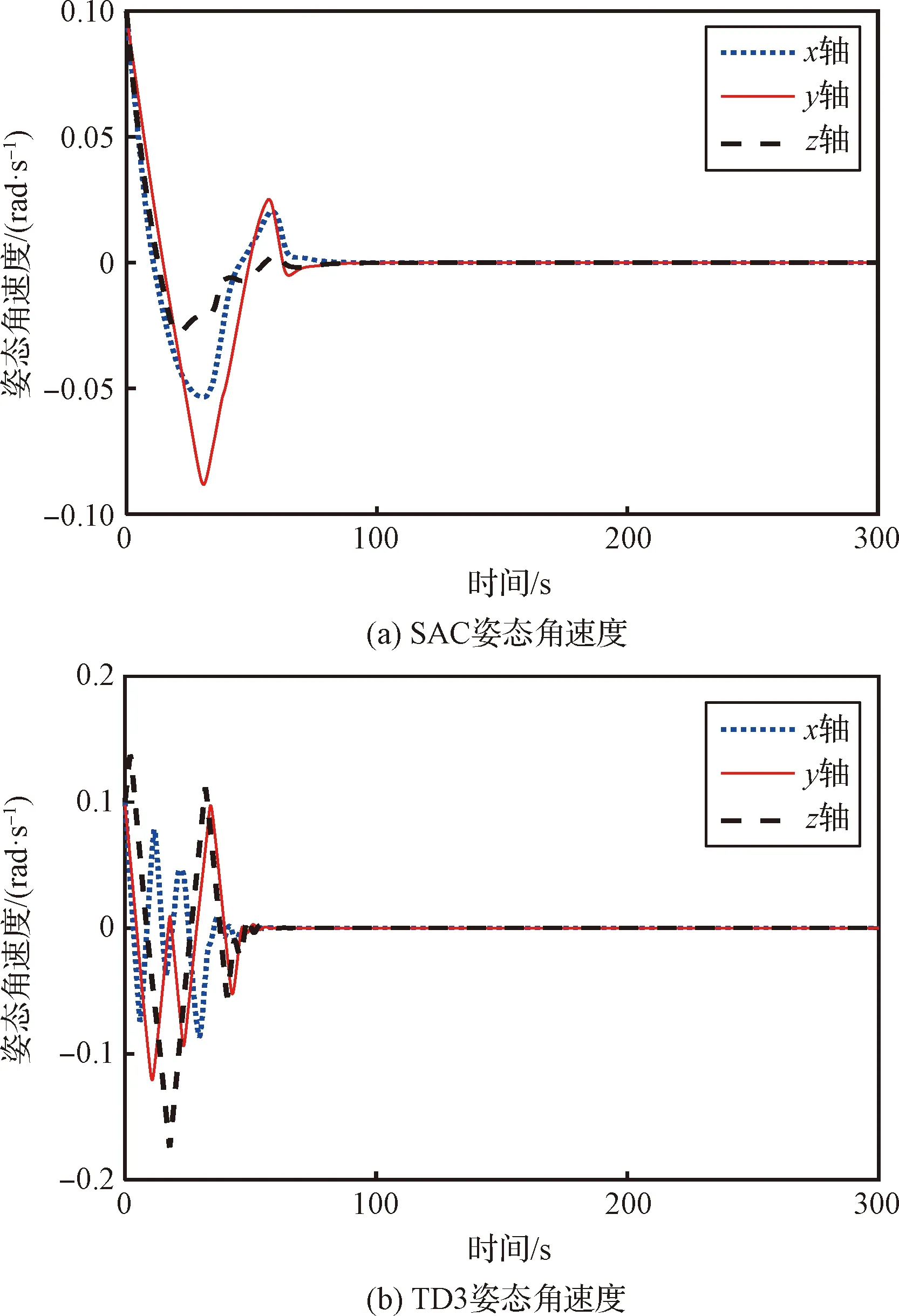
图9 姿态智能控制器部署后的姿态角速度曲线

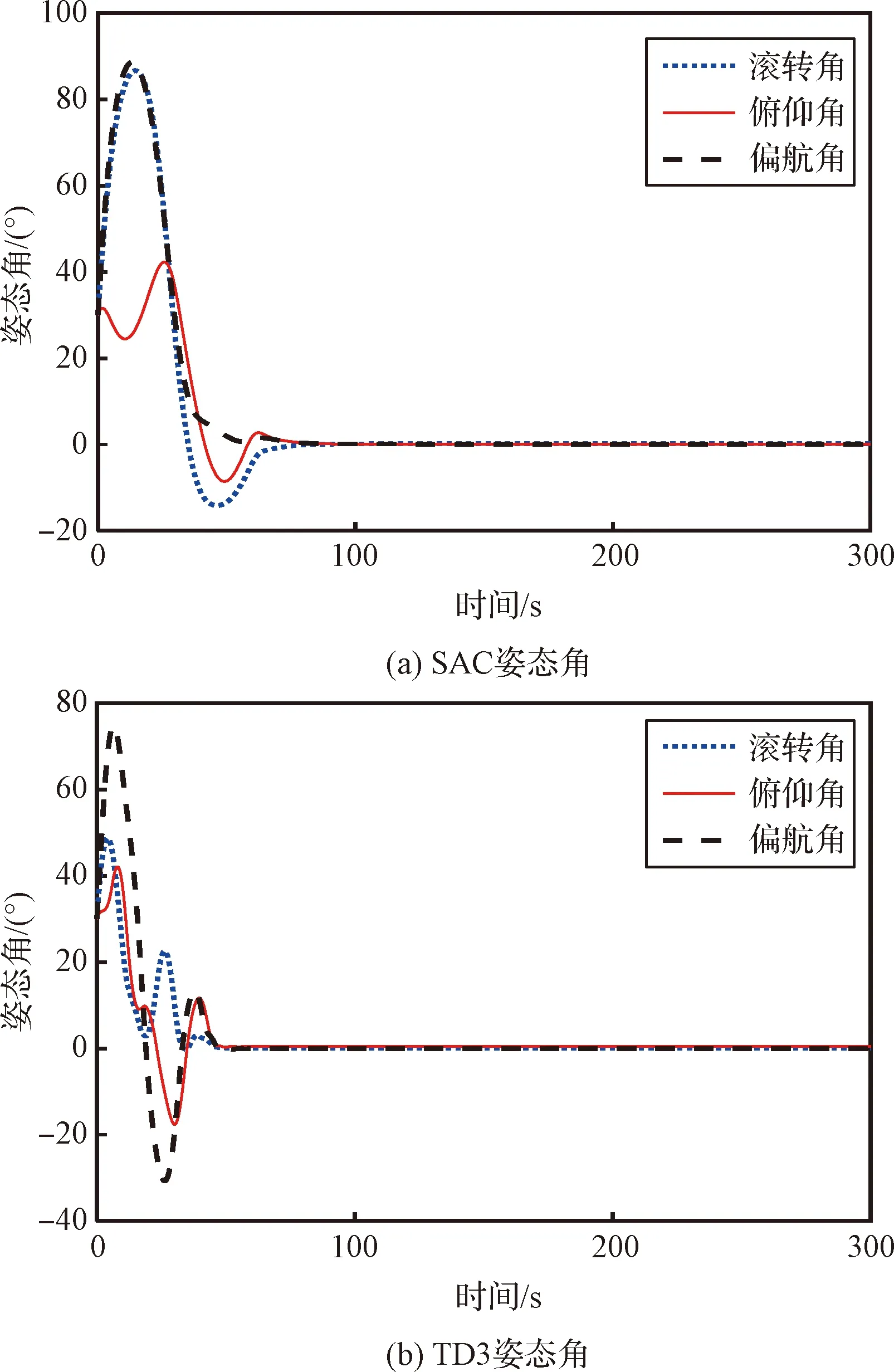
图10 姿态智能控制器部署后的姿态角曲线

4.2 SAC加注压强智能控制器训练和部署仿真

将SAC姿态智能控制器部署到在轨加注组合体的姿态控制系统中,进一步对SAC加注压强智能控制器进行训练和部署。在对加注压强智能控制器的训练中,在轨加注组合体的相关参数见表4。

表4 加注压强智能控制器训练算例在轨加注组合体参数

SAC加注压强智能控制器的关键训练参数见表5。Actor和Critic网络参数与SAC姿态智能控制器保持一致,如图4所示。

表5 SAC加注压强智能控制器的关键训练参数

对SAC加注压强智能控制器进行训练。训练过程中,SAC加注压强智能控制器获得奖励值的曲线如图11所示。SAC加注压强智能控制器共进行120轮训练。前60轮训练奖励值逐步攀升,说明SAC加注压强智能控制器不断对策略做出优化。后60轮训练,奖励值趋于稳定,在波动中有小幅提高,说明加注压强智能控制器已经得到最优控制策略并对最优控制策略做出小幅的调整。

图11 加注压强智能控制器训练奖励值曲线

在部署完成训练的SAC加注压强智能控制器时,仍需按照式(24)对动作的输出进行调整。调整动作输出后,SAC加注压强智能控制器输出的加注压强如图12所示。在加注过程的前35 s,由于SAC姿态智能控制器还未控制姿态达到稳定,仍存在随机扰动作用,所以,加注压强进行了自主的波动调整,尽量减小随机扰动对姿态的影响。在姿态逐渐稳定之后,加注压强保持在0.095 Pa,从而尽可能高效地完成加注任务。在140 s时,加注的液体质量达到任务要求,加注管理系统给加压系统关机信号,加注压强归零。采用与未采用加注压强智能控制条件下,随机扰动的模如图13所示。在采用加注压强智能控制后,随机扰动的最大幅值相较于未采用加注压强智能控制时减小了4倍;并且,在整个加注过程中,采用加注压强智能控制时的随机扰动也均小于未采用加注压强智能控制时的随机扰动。观察加注压强的曲线发现,当随机扰动出现较高峰值时,SAC加注压强智能控制器都相应地降低了加注压强的输出;这说明,SAC加注压强智能控制器可以自主地根据随机扰动调节加注压强,从而有效地减小液体加注对姿态产生的影响。

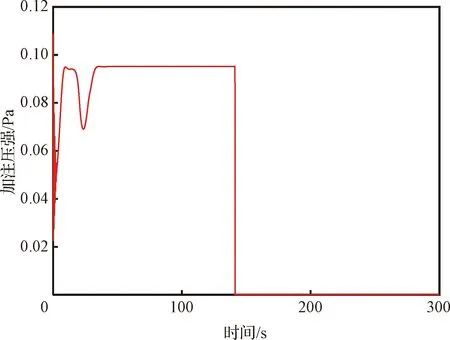
图12 加注压强智能控制器输出曲线

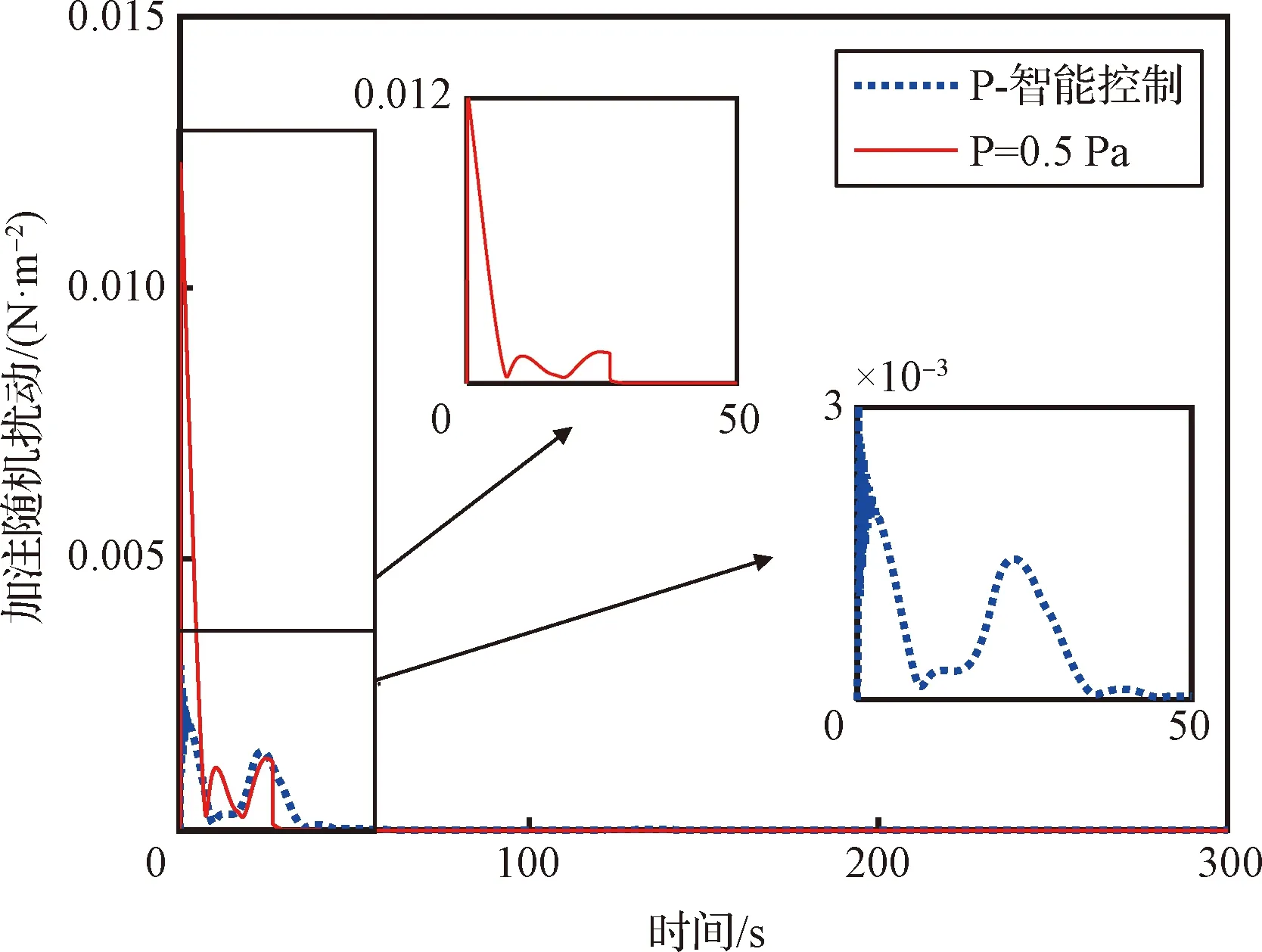
图13 采用与未采用加注压器智能控制的随机扰动对比

5 结 论

本文针对在轨加注任务中,由液体复杂运动引起组合体姿态随机扰动,以及“一对多”加注过程中组合体惯量参数不确定的问题,通过改进深度强化学习SAC算法,设计了SAC姿态智能控制器和SAC加注压强智能控制器。SAC姿态智能控制器以小幅值的控制力矩使组合体姿态平稳收敛,避免了控制力矩和姿态大幅波动的现象,在应对不同结构目标星和系统随机扰动方面具有很强的鲁棒性。SAC加注压强智能控制器可以根据随机扰动智能地调节输出的加注压强,在高效完成加注任务的同时,有效地减小液体燃料加注对姿态产生的扰动。通过仿真算例对上述结论进行了对比验证。