空间多体绳系编队动力学与控制研究综述

王长青，杨 航，孙佩杰，李爱军

(西北工业大学自动化学院，西安 710072)

0 引 言

空间多体绳系编队是由空间双体绳系系统演变而来,通常由多个卫星或航天器通过特殊材质系绳连接组成的某种特定构形的编队系统[1-3],如图1所示。空间多体绳系编队系统在进入预定空间轨道后,会根据任务要求展开形成相应的编队构型,在编队系统中,一些大型航天器可由多个结构简单的卫星代替,卫星之间可以通过通信来进行信息共享。此外,空间多体绳系编队系统还可以根据任务需求及变化,通过改变系绳长度等方式完成编队构型重组,以实现不同类别任务的目标。相比于无绳系编队系统,多体绳系编队系统的主要优势一方面在于这种系统可通过调整系绳张力来保持或改变队形,而传统的编队系统在队形控制过程中需要依靠推进器产生推力,会消耗大量燃料;另一方面绳系编队卫星系统可获得较长的测量基线,并通过收放系绳来改变测量基线。相对于传统的自由编队方式,空间多体绳系编队系统的研究虽然起步较晚,但其巨大的应用前景已经得到学术界以及工程界的广泛认可,被认为在空间目标捕获[4]、在轨服务[5-6]、空间干涉仪[7]、电子监视等[8]多方面具有很高的应用潜力和价值。例如近些年来世界各国开展的大量在轨绳系卫星试验,包括NASA的SEDS系列、俄罗斯和欧洲联合进行的YES2空间试验以及美国ISAS与日本JAXA合作开展的T-REX等太空试验[9-11],均验证了空间绳系系统太空任务的可行性和应用前景。

图1 空间多体绳系编队系统

空间多体绳系编队运行于特殊的太空环境,不仅构形种类繁多,还存在较为复杂的动力学特性,因此需要对编队构型、动力学模型、编队构型形成、编队构型稳定保持以及星体姿态机动等方面展开研究。本文介绍了常见的绳系编队构型及其特点,对常见的绳系系统动力学模型进行了总结;梳理了绳系编队任务全流程控制研究现状,包括绳系编队构型形成控制、构型稳定保持研究以及刚体姿态机动控制;分析总结了现有的地面试验装置及方法,展望了未来的发展趋势。

1 空间多体绳系编队构型及动力学模型

1.1 绳系编队构型

空间多体绳系编队系统因航天器个数的不同而存在多种构型组成方式,在进入到预定空间轨道之后,多体绳系编队系统会根据不同的空间任务要求产生不同的构型。绳系编队的构型一般按照末端体在空间的分布形式或编队稳定飞行方式进行分类。按照空间分布形式可分为三大类:一维构型、二维构型和三维构型。其中一维构型即卫星均位于一条直线上,属于此类构型的绳系编队系统称为直链式构型[12-13],如图2所示;二维构型即在空间中卫星位于同一平面内,常见的此类构型有闭环三角形构型[14]、开环-轮辐式构型[15]、闭环-轮辐构型[16]以及TetraStar构型[17]等,如图3所示;三维构型即系统中的卫星处于不同平面的构型,研究较多的此类构型包括四面体构型[18]、双四面体构型[19]、金字塔构型[20]以及双金字塔构型[21]等,如图4所示。

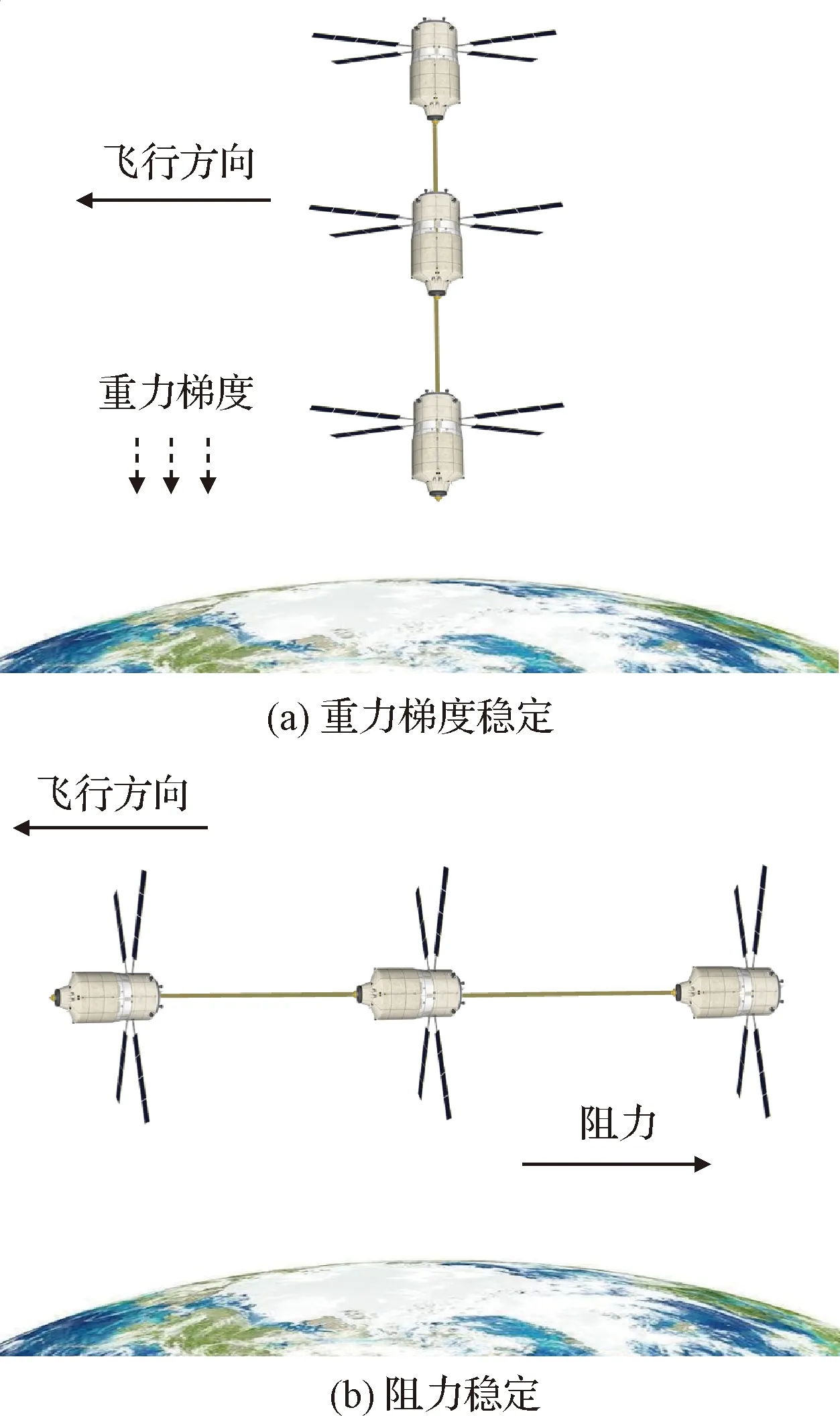
图2 一维构型

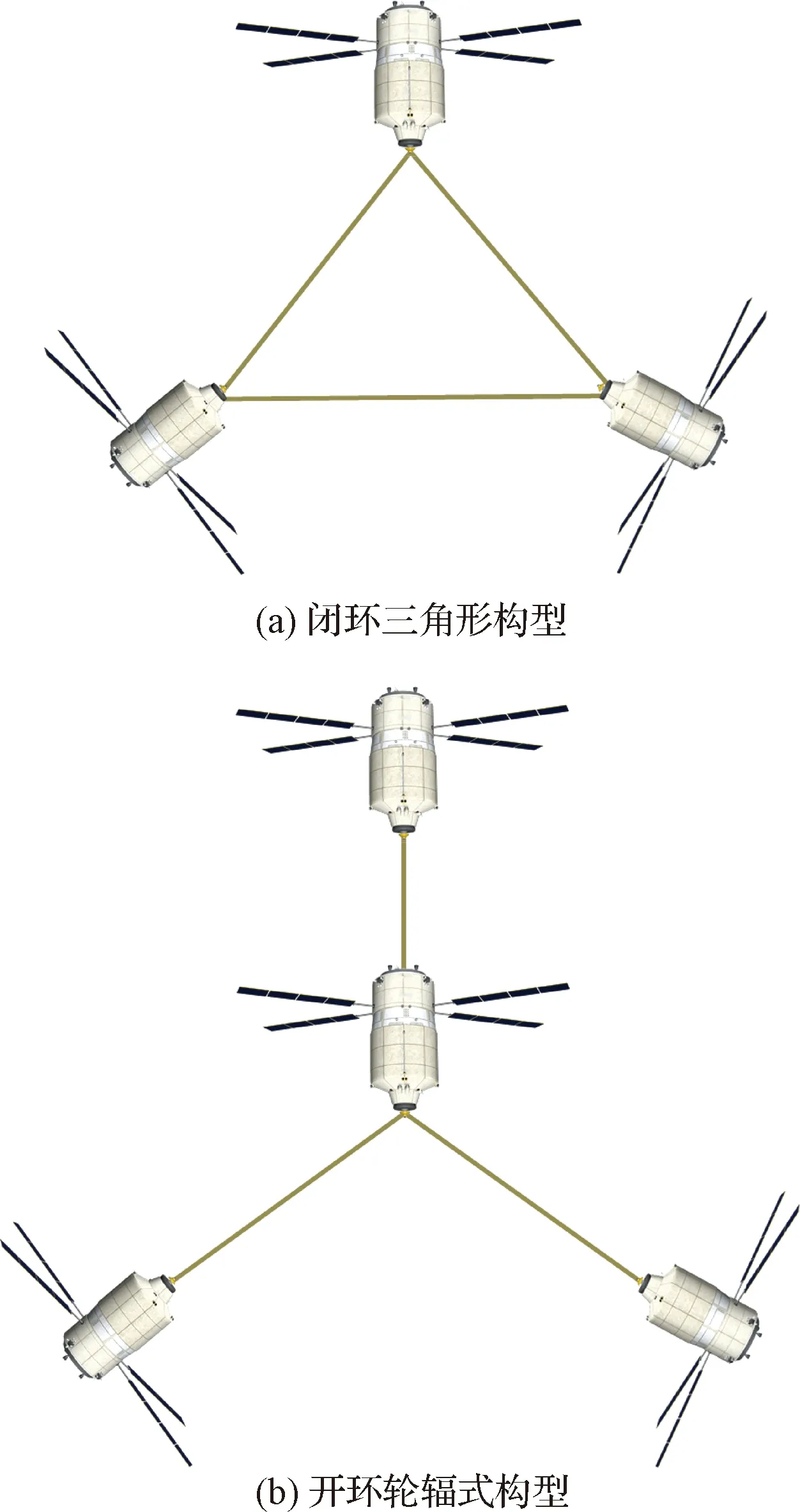
图3 二维构型

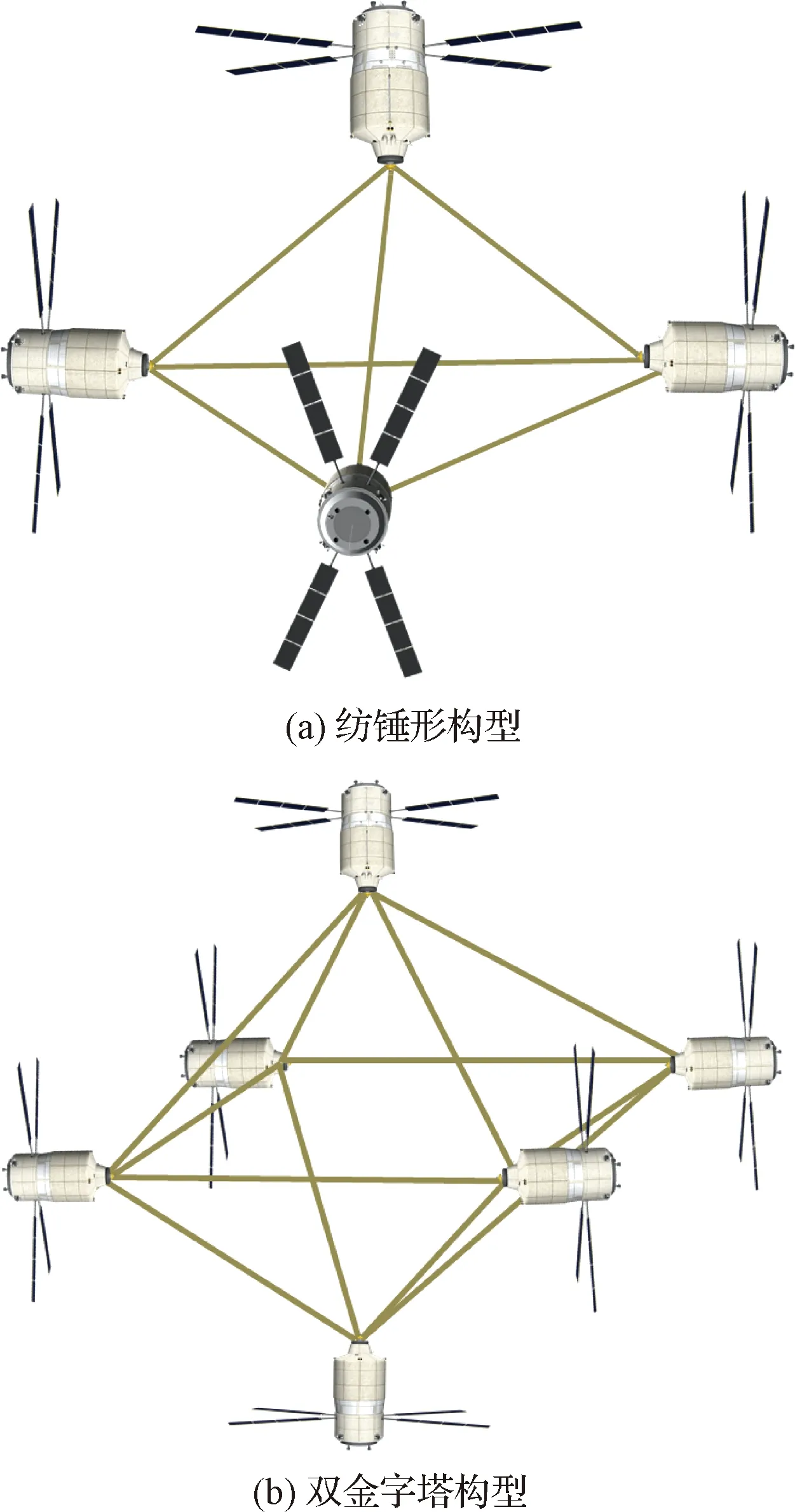
图4 三维构型

按照绳系编队的稳定飞行形式,系统还可以分为静态构型和动态构型两大类[22]。在静态构型编队中,整个编队系统与轨道坐标系保持相对静止。静态构型编队主要以重力梯度、阻力以及电磁力等方式来保持构型的稳定,例如图2所示的一维重力梯度稳定构型、一维阻力稳定构形。对于动态构型,编队系统会相对于轨道坐标系进行旋转运动,从而使得系绳拉紧来实现整个编队系统的稳定。例如二维离心力稳定构型、三维离心力-重力稳定构型,如图5所示。

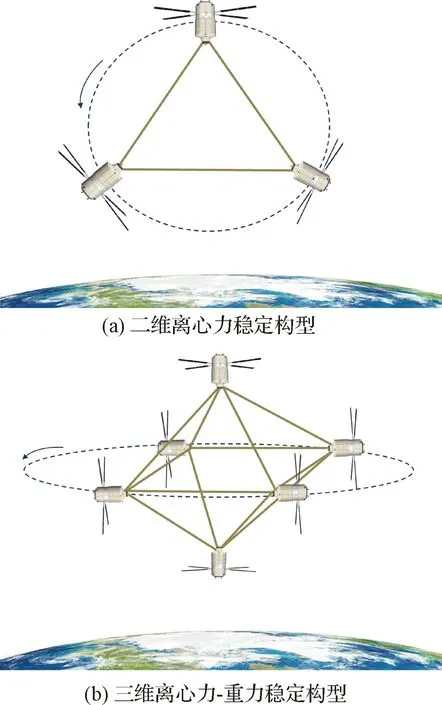
图5 多维动态构型

动态构型编队为了使系绳在编队中保持张力,系统必须旋转。在张力的作用下,整个系统会产生刚性作用,即系统可以被视作刚体。相反,如果系绳没有张力,或者当系统在拉紧和松弛状态之间变换时,各星体之间会发生碰撞或缠绕等事故。如图6所示,对于在圆轨道上轴对称旋转的绳系编队系统有三种相对平衡:圆柱形平衡、双曲线平衡和圆锥形平衡,在这种平衡下,整个编队系统自旋轴以与轨道运动相同的速度旋转[23]。在这三种平衡状态中,圆柱形平衡态自旋轴垂直于轨道平面,双曲线平衡态自旋轴垂直于当地垂线,编队运动在地球上的投影是一条直线,因此这两种平衡态不适用于绳系编队对地球进行观测。而对于圆锥平衡,其自旋轴垂直于轨道切线方向,其运动投影到地球表面将呈椭圆形,可以增大对地球的观测范围。

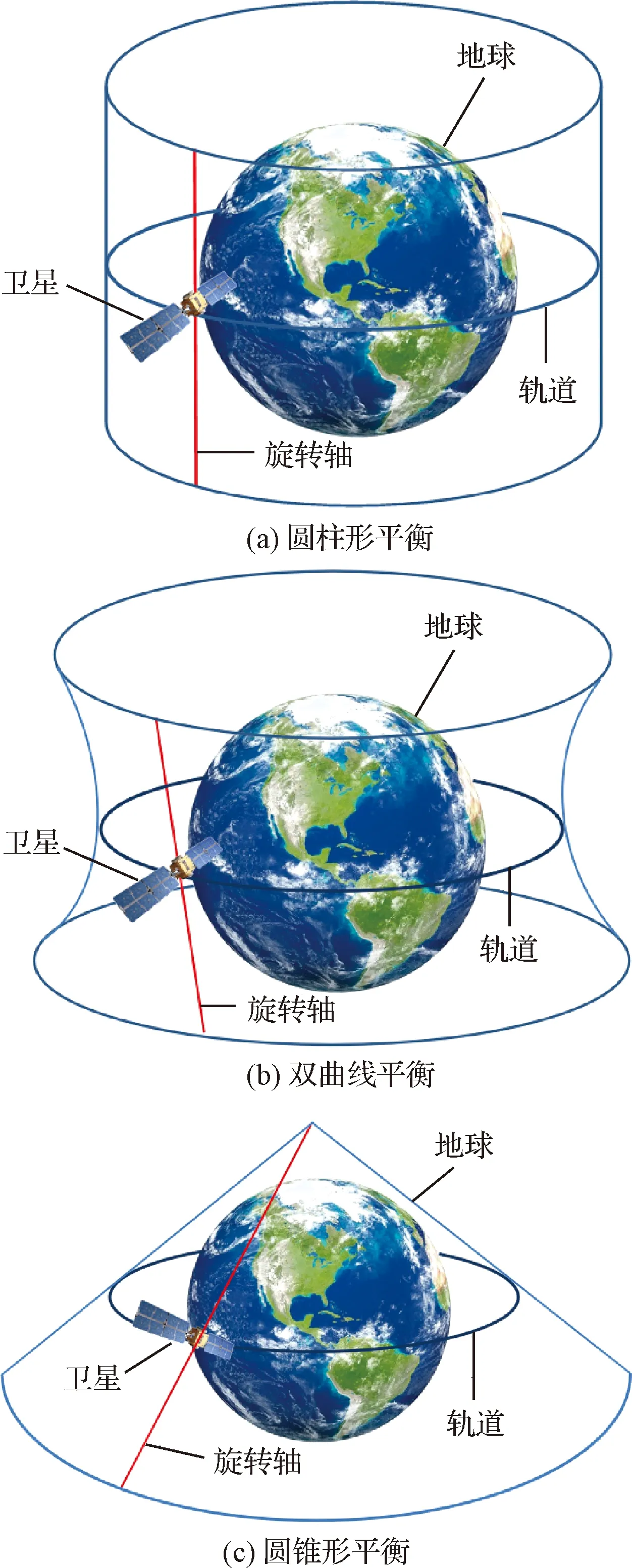
图6 相对平衡状态

不同构型的绳系编队具有不同的结构特性,例如系统稳定方式、适用任务场景等。余本嵩等在文献[24]中对不同构型下的绳系编队系统稳定性进行了总结,如表1所示。本文查阅了从2000年至2022年期间的多篇空间多体绳系编队研究文献,参考了102篇较为权威的文献,给出了不同构型绳系编队的文献研究数量对比,其中一维构型绳系编队研究占比38%,二维构型研究占比52%,三维构型占比10%。在二维构型绳系编队中,三角形构型和轮辐式构型是研究热点,占比分别达到了49%和34%。可以看出,目前对于空间多体绳系编队系统的研究主要集中于一维构型和平面式构型,而空间构型由于结构比较复杂,模型的复杂程度较高,因此对于该类构型研究较少。

表1 不同构型下的绳系编队系统稳定方式[24]

1.2 系绳模型

系绳模型建立是空间绳系系统研究的基础,目前应用最广泛的系绳模型主要包括三种,刚性杆模型、弹性杆模型以及珠点模型。在早期的研究中,研究人员通常将系绳看作刚体,不考虑系绳的弹性和柔性,这种简易的模型主要用来设计系统的标称展开轨迹。随着研究的不断深入,学者们又提出了弹性杆模型,这种模型将系绳看作一种只能在受拉时产生拉力而无法在受压时产生弹力的“弹簧”,相当于只考虑了系绳的纵向振荡。但实际的系绳除了在纵向会产生振荡,在横向也会有振荡。针对这种情况,研究人员建立了系绳的珠点模型,将系绳看作一个个珠点,珠点之间通过弹性杆连接,这种模型也是现在研究中常用的相对精确的一种系绳模型。

1.2.1刚性杆模型

刚性杆模型是一种较为简单的系绳模型,如图7所示,该模型忽略了系绳的弹性和柔性,将其视为一根不可拉压的刚性杆,即系绳刚度趋于无穷大,两端分别连接着系统中的不同航天器。

图7 刚性杆模型

刚性杆模型在90年代被众多学者提出,主要用于双体绳系系统的标称展开轨迹设计[25-26],之后诸多学者将刚性杆模型拓展至多体绳系编队模型的建立,通过简化系绳模型,对绳系编队飞行的可行性以及动力学进行分析。Tragesser等将刚性杆模型分别用于任意数量卫星的环形绳系编队和双金字塔型绳系编队标称轨迹的设计[27]。之后Kumar等忽略了系绳质量、阻尼效应以及横向振动,通过所提出的约束系统非线性运动控制方程的数值模拟结果和平衡分析,验证了在轨道平面上实现三角形编队飞行的可行性[28]。以上研究均未考虑平台姿态,Menon等将系绳建模为刚性杆模型,考虑了星体姿态,研究了编队中各平台姿态的动力学和控制[29]。由于平动点在深空探测中有巨大的应用前景,众多学者对平动点轨道上的绳系编队动力学特性进行了深入研究。Sanjurjo-Rivo等利用刚性杆模型,研究了绳系编队系统在日-地平动点处的动力学分析,并给出了几个稳定系统的控制律,为绳系系统在太空探索提供了一定的理论支撑[30]。Cai等[31]考虑系绳为不可伸展且忽略质量的刚性杆,分析了一种轮辐式绳系卫星编队在平动点附近的动力学,并基于希尔近似,提出了一种新的非旋转或旋转绳系编队的动力学公式。在此基础上,Cai等[32-33]又对闭环三角形绳系编队动力学稳定性进行了深入研究,分析了轨道振幅、旋转速率以及系绳长度等参数对系统稳定性的影响。为了研究日地平动点绳系卫星编队的重定向控制,Luo等[34]利用刚性杆模型,设计了用于系统状态和控制输入的标称轨迹。Huang等[35]研究了一种轮辐式绳系机器人编队系统,忽略了系绳质量和弹性等影响,提出了一种系绳张力和主星扭矩的协同控制策略。之后,又在另一种轮辐式绳系编队建模中,采用刚性杆假设,研究了系绳的展开和回收问题[36]。Zhai等[37]针对众多研究中未考虑星体和系绳之间的耦合问题,基于刚性杆模型,考虑了星体自转与系绳展开之间的耦合,研究了轨道平面内轮辐式绳系编队的展开控制问题。Chen等[38]将编队系统建模为质点-刚性杆系统,对近地轨道上三角形绳系纳米卫星系统的展开问题进行了研究。Wang等[39]假设系绳为刚性杆,针对线性绳系卫星编队系统设计了分阶段展开的方案,利用Lagrange方程建立了编队系统的标称模型,通过参数优化得到了绳系卫星编队系统的标称轨迹。Zhang等[40]基于简化的刚性杆模型,分析了直链式绳系编队在构型转换过程中的非线性动力学特性。

1.2.2弹性杆模型

在实际情况下,系绳会随着所受外力的变化而发生形变,进而产生内应力。因此学者们又引入了较刚性杆模型更为贴合实际绳系系统的弹性杆模型。如图8所示,弹性杆模型考虑了系绳的弹性而忽略了其柔性,将系绳视为一根不会弯曲的直杆。

图8 弹性杆模型

Pizarro等[41]考虑系绳弹性并将星体近似为质点,研究了开环和闭环两种轮辐式结构绳系编队的动力学,使用Lagrange方法推导了两个系统的运动方程。Williams等[42]基于弹性杆模型,提出了一种考虑轨道运动、系绳弹性以及重力梯度效应的三角形绳系编队动力学模型,该模型被众多学者在研究三角形绳系编队时采用[43-45]。耿凌璐[46]考虑系绳弹性杆模型,利用Newton第二定律建立了三角形绳系编队在非惯性参考系下的动力学方程,研究了J2摄动、热效应等因素对编队稳定性的影响。Qi等[47]考虑系绳弹性,利用Lagrange方程得到了一种库仑双金字塔绳系编队的运动方程,探讨了该编队应用于地球同步卫星配置的可行性。Zhang等[48]也提出了一种金字塔型绳系库仑编队,考虑弹性杆模型,并利用Lagrange方程推导了编队的动力学模型。Huang等[49]在Williams的研究基础上,考虑系绳弹性,利用Lagrange方程建立了三角形绳系编队动力学模型,并提出了一种基于滤波器的状态估计方案,解决了绳系编队状态测量的问题。基于该模型,Su等[50]进行了一系列三角形编队动力学特性以及稳定展开控制研究,计算出了编队自旋稳定时的自转角速度范围,为后续的编队控制提供了很好的理论支撑。

1.2.3珠点模型

珠点模型将系绳离散为一系列由无质量弹簧连接的质点,两端分别与主星和子星相连接,如图9所示。随着所选取的离散点的数量越多,模型与真实系绳系统越接近,但同时也使系统变得复杂,同时增大了理论研究的难度与仿真运算的时间。

图9 珠点模型

Yan等[51]首次将系绳珠点模型应用在直链式构型绳系编队中。之后,Tragesser等将这种模型用在了闭环自旋多体绳系卫星编队和双四面体型绳系编队上面,用于实现地球定向观测任务[27]。Nakaya等[52-53]也将珠点模型用于三角形绳系卫星编队系统上,并提出了释放新珠点时克服系统不连续性的方法。Williams等在文献[54]中也利用珠点模型对三角形绳系编队的动力学进行了分析,并将其拓展至双金字塔型绳系编队。为了更加清晰的描述系统的动力学响应进而分析控制系统的性能,在基于该模型对绳系系统进行研究时,研究者们一般采用Galerkin模态法[55]和有限元法[56]完成方程的离散化。刘壮壮等[57]考虑了系绳的密度非线性、非线性弹力以及空间摄动因素的影响改进了珠点模型,并定量分析了执行任务时系绳的横纵向振动。余本嵩等[58]在前人研究的基础上提出了一种时变的珠点模型,随着系绳的不断展开,系绳上的珠点也不断的增加。为了突出系绳质量对系统动力学的影响,Avanzini等[59]利用珠点模型建模获得的结果与简单无质量系绳模型进行比较,结果表明系绳质量对封闭构型的编队动力学产生较大影响。之后,Avanzini等又在文献[60]中利用珠点模型分析了轨道偏心率对闭环绳系编队的影响。Luo等[13]将系绳建模为珠点模型,基于希尔近似,开发了一种新的柔性多体绳系编队动力学模型,该模型可应用于任意构型的N体绳系卫星编队系统。基于该模型,Luo等[34]又研究了日地平动点直链式绳系编队的重定向控制。

通过前人的研究可以看出,虽然刚性杆模型和弹性杆模型无法反映真实情况下的绳系系统状态,但有利于降低控制器设计难度并提高计算效率,便于对系统进行一些简单直接的分析,因此被广泛应用于绳系系统控制方法验证、标称轨迹设计等研究。当需要提高模型精度时,则需要同时考虑系绳质量、弹性、形变等因素,从而建立更加精确的珠点模型。虽然珠点模型的精确度较高,更加贴切实际任务场景中的系绳,但是该模型的复杂度很高,会导致计算耗时很长,不便于对系统进行分析。所以大部分研究者会先使用系绳较为简单的刚性杆模型、弹性模型来验证猜想,然后在珠点模型上施加实际控制器得到验证。

2 空间多体绳系编队全流程控制

空间多体绳系编队在进入太空后,根据任务控制需求可分为三个部分,包括绳系编队构型形成控制、构型稳定保持以及星体姿态机动控制。

2.1 空间多体绳系编队构型形成控制

编队构型形成是空间多体绳系编队一切应用技术的基础,包括实现绳系编队系统的快速稳定展开、回收。此外,针对不同的太空任务,绳系编队还可能通过编队重构形成其他编队构型。为使绳系编队按照合理的方式完成构型形成,达到系绳与航天器之间不发生缠绕、尽可能的节省燃料等实际目标,需要对系绳展开方案进行具体的设计。目前已经有许多关于绳系编队展开及回收的研究,控制方法主要有张力控制、长度控制以及速度控制等。Nakaya等[52]基于虚拟结构方法,使用预先确定的角动量分布以及系绳张力分布来计算自旋角速度,从而实现三角形绳系编队的展开。Williams等[61-62]利用张力控制确定了不同自旋条件下的最佳展开和回收轨迹,并对系统旋转速率和机动时间的影响进行了参数研究,数值结果说明了系绳展开和回收的对称性。Liu等[63]针对轮辐式构型绳系卫星编队开发了一种纯张力控制策略,以抑制展开过程中的系绳振动,而不向子卫星施加推力,最终系绳能够完全稳定地展开到所需的轮辐式结构。刘丽丽等[64]研究了轮辐式三体绳系卫星编队面内飞行时的最优回收控制问题,针对不同回收初值及受扰情况,计算了绳系卫星编队飞行的最优控制张力和飞行轨迹。考虑到张力控制的局限性,Chen等[38]提出了一种系绳张力和外部低推力结合的控制律,在实现稳定展开的同时保证了控制律的简洁性和有效性。Kumar等[65]设计了一套绳长控制律,使三体直链式绳系卫星编队可以沿水平方向逐一稳定展开/回收。文献[66-67]针对日地平动点附近的轮辐式旋转绳系卫星编队,利用数值仿真研究了编队重构阶段的动力学稳定性。苏飞等[68]针对圆轨道上的开环轮辐式绳系卫星编队,分别研究了在重力梯度力补偿和无补偿两种情况下的自旋展开控制策略,通过速度控制实现了绳系编队的有效展开,仿真结果表明两种展开控制策略能够保证编队稳定展开。以上针对系绳的展开控制研究均未考虑星体姿态运动对系绳的影响,于是,Zhai等[37]针对一种开环轮辐式绳系编队,考虑到了母星的自旋运动与系绳展开之间的耦合,研究了轨道平面内自旋稳定绳系编队的展开控制问题,并且开发了具有重力梯度补偿的控制策略。黄攀峰等针对三角形绳系编队展开问题进行了深入研究,在文献[69]中定量分析了编队自旋稳定时的自转角速度范围,为之后的稳定展开控制提供了理论依据。由于针对绳系编队状态估计的研究较少,Huang等在文献[70]中研究了具有状态观测器的绳系编队的稳定展开,针对系统速度不可测的情况,给出了一种高增益观测器来对速度变量进行估计。之后,Huang等[71-72]又针对在实际空间环境中绳系编队可能存在的通信资源受限问题,基于事件触发机制设计了一系列展开控制策略,不仅可以实现编队的稳定展开,还能减少对通信资源的消耗。

2.2 空间多体绳系编队构型稳定保持

绳系卫星编队系统构型稳定性是绳系编队领域的研究重点和热点,由于太空中重力梯度力和低轨道高度下的空气阻力的存在,一维线性构型绳系编队能够满足重力梯度力稳定和阻力稳定的条件,并保持线形的构型稳定。Misra等[73]研究了直链式构型编队系统在构型形成过程中的四种平衡位置及其稳定性,验证了其中沿当地垂线的平衡位置是稳定的。Avanzini等[59]从Misra的研究结果出发,对一种由四颗卫星连接得到的编队系统进行了研究,得出除了四颗卫星共线的平衡方式外,还有16种平衡解决方案的特殊情况。在线形构型的基础上,又有学者研究了多颗卫星平面排布的平面构型方法。Tragesser等在文献[74]中基于锥形Likins-Pringle相对平衡的轨道设计,研究了具有任意数量卫星的环形编队系统稳定性。Kumar等[28]对一种三角形绳系编队稳定性进行了研究,实验结果证明要使系统稳定则需要编队旋转速率与轨道角速率的比值不能小于0.58。Pizarro等[75]对Y字型轮辐式绳系编队和闭环十字型绳系编队稳定性进行了研究,发现当编队在轨道平面上旋转时,对于具有四颗星体的轮辐式构型是稳定的。当星体数量超过4颗后,则需要外部系绳构成闭环式编队才能保持稳定。陈志明等[76-77]根据力学方法证明了Thomson平衡下绳系卫星编队系统自旋角速率与轨道角速率的比值在0.61和2.61之间时,系统可以保持稳定。Yu等[78]使用Floquet理论得到了使旋转三角形编队系统留位状态稳定的初始速度取值范围。蔡志勤等[79]深入研究了位于日地平动点附近的旋转三角形绳系编队系统的动力学与控制问题,重点分析了编队系统在构型形成和保持时的稳定性,研究结果均表明三角形绳系编队可以通过旋转保持稳定。

在平面构型的基础上可以构建更为复杂空间编队构型,并通过自旋和重力梯度力等使其在绕地飞行中保持稳定。Sabatini等[80]对一种双金字塔构型绳系编队进行了稳定性研究,认为该种构型保持稳定的条件极为苛刻,在真实条件下很难成功。Williams等[54]也对双金字塔构型绳系编队系统进行了动力学仿真研究,从其结构特点出发,对在旋转轴与地面垂直时的运动稳定性进行了研究。Avanzini等[60]对一种由重力梯度力及其自旋离心力共同作用保持稳定的双四面体绳系编队的稳定性进行了研究,并对其构型稳定性的保持进行了控制。基于双金字塔型稳定性的研究,黄攀峰等[81]首次提出了双金字塔绳系卫星编队的状态估计方案研究。

2.3 空间多体绳系编队姿态机动控制

绳系编队运行在太空中,针对不同的任务需求,编队星体往往需要进行一些姿态机动来达到理想的工作位置。由于编队各星体通常具有较大的质量和尺寸,因此星体姿态运动对系统产生的影响不可忽视。目前对空间绳系系统姿态动力学的研究主要聚焦于双体绳系系统,在很多利用双体绳系系统进行碎片捕获、轨道转移等研究的文献中,均对星体的姿态动力学进行了深入分析。然而多体绳系编队由于结构复杂,大部分研究均考虑星体为质点,对于姿态动力学的研究还较少。Lemke等[82]首先探索了通过利用系绳张力提供的扭矩来控制绳系卫星姿态的可能性。Modi等[83]研究了绳系卫星编队刚体平台的姿态动力学和控制,并基于Lyapunov第二种方法提出了一种非常有效的偏移控制算法。Nakaya等[52]将卫星视作刚体并考虑其姿态,使用虚拟结构法实现了三角形绳系卫星编队的展开控制。Chung等[84-85]利用分散控制讨论了多体绳系编队的自旋速率以及卫星刚体姿态控制问题,这是第一次提出了用于绳系编队的无推进剂欠驱动控制方法,并基于麻省理工学院SPHERES试验台进行了验证。Chang等[86]研究了一种三体直链式绳系编队,并且考虑了每一个星体的姿态,采用状态相关的Riccati方程(SDRE)控制器调节姿态误差,并将集中式和分散式方法应用于动态系统,仿真验证了SDRE控制器用于绳系卫星姿态控制具有良好的控制性能。苏飞等[68]和Zhai等[87]均考虑到母星姿态与系绳展开之间的耦合关系,对辐射开环形绳系编队稳定展开控制进行了研究。Sun等[88]提出了一种任意数量的直链式绳系卫星编队,考虑了母星姿态运动,利用绝对节点坐标公式(ANCF)和自然坐标公式(NCF)分别用于精确描述柔性系绳和刚性卫星的大变形和大整体运动。Luo等[34]考虑卫星的姿态运动,研究了日地L2平动点处柔性多绳系卫星编队重定向控制,所建立的灵活模型可用于描述具有任意结构的多绳系卫星编队系统。考虑到系绳的摆动问题,贾程等[89]基于母星的姿态机动,通过调整母星推力方向实现了绳系卫星编队系统轨道跟踪。Chen等[90]考虑了母星旋转与系绳展开之间的耦合效应,建立了轨道平面上轮辐式构型绳系编队的动力学模型。并基于Bellman动态规划方法,考虑了展开过程中系绳张力的物理约束,提出了一种最优控制器,通过数值仿真验证了所提控制策略的有效性。

3 绳系系统地面试验

由于太空任务复杂,成本高昂,因此在进行太空任务前需要进行充分的研究与试验,而地面模拟试验对在轨绳系系统的研究起到非常重要的作用。目前国内外已经开展了多种空间多体绳系编队系统的地面试验研究方案。

3.1 地面气浮平台法

气浮平台法具有建造周期短、成本低、易于实现及维护等优点,通过设计平板止推轴承的大小能够实现高达几吨的飞行器微重力实验,且实验的时间不受限制。通过更换接口部件即可实现重复利用,可靠性和鲁棒性较高,对飞行器结构没有太多限制,且根据不同实验目的可以较为容易地进行二次设计和改造。地面气浮台作为一种结构简单、成本较低的试验装置,已经被诸多学者应用于空间绳系系统的地面试验验证,是目前绳系系统地面试验应用最广泛的一种方法。

Nakaya等[91]为了研究空间绳系卫星编队问题,提出了实现旋转三角形绳系编队构型形成的方案,如图10所示。由同时发射的航天器(步骤a)组成的初始系统,通过系绳展开(步骤b)形成稳定的编队构型(步骤c)。为了验证所提出方案的可行性,Nakaya等开发了一套在地面情况下用于模拟绳系编队的气浮平台系统,该系统包含气浮平台、三个卫星模拟器和一个CCD相机组成的位置测量子系统,最终成功实现了三角形绳系卫星编队的稳定展开。

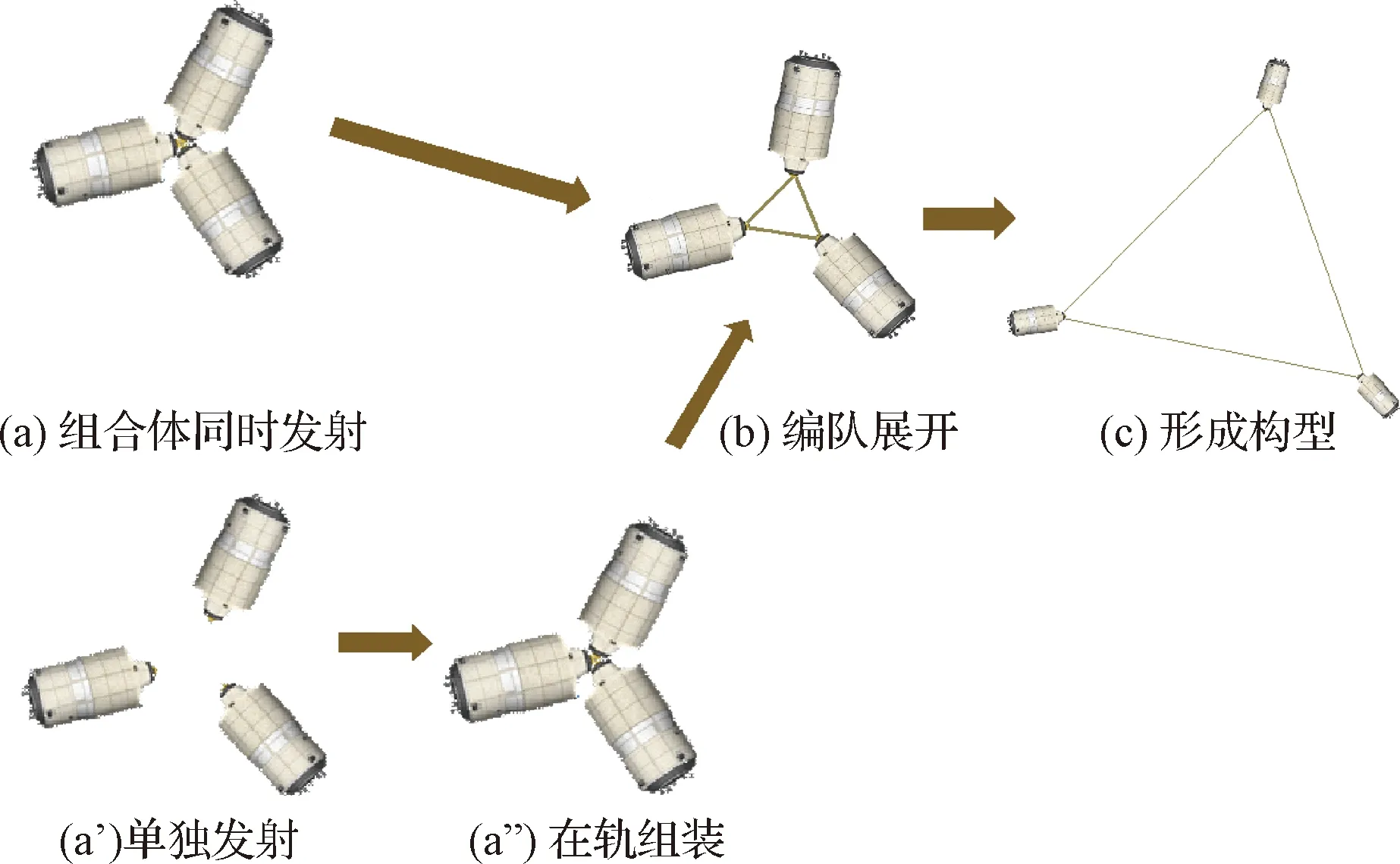
图10 绳系卫星编队构型形成方案[91]

麻省理工学院空间系统实验室(MIT-SSL)开发了名为SPHERES的多颗纳米卫星试验台,主要用于编队飞行和自主对接、交会和重构算法试验验证[92]。在该平台基础上,Chung等[93-94]成功进行了一系列直链式、三角形绳系编队系统的旋转展开动力学试验,验证了在未来的空间干涉仪任务中不依赖推进器的情况下控制绳系编队的可行性。之后,Chung又在文献[95]中使用多颗SPHERES微型卫星对绳系编队飞行的一些关键控制策略进行了试验验证。基于该平台,Mantellato等[96]开发了一个用于模拟双质量绳系系统在轨动力学的软件模型,并通过SPHERES平台对软件模型进行了验证,为后续在太空微重力环境开展更精确的试验进行了预研。Iki等[97]通过电动力绳系(Electro-Dynamic Tether,EDT)系统的数值模拟,利用气浮台研究了使用推进器从卷轴式卷筒上展开系绳。推进器用于确保展开长度为数公里的系绳,通过地面试验评估了几个关键的参数,如推力和推进器激活周期,明确了展开所需推进器的要求,该装置主要用于研究EDT技术进行轨道转移的主动碎片清除系统。

为了研究绳系编队动力学问题,金栋平等[98]为空间绳系系统研究建立了气浮平台设施,该平台可以模拟绳系系统所经历的微重力场,通过使用平面空气轴承试验台和科里奥利力,在反馈控制下使用机载推力。之后,该团队利用动态相似原理构造了等效地面试验系统[78],该系统由花岗岩试验台、三个由系绳连接的卫星模拟器和一个立体视觉测量系统(SVMS)组成,如图11所示。基于该试验系统,该团队研究了在近地轨道上飞行的三角形绳系卫星编队的旋转稳定性,成功实现了直链式构型和三角形构型绳系编队的稳定展开和保持。

图11 绳系卫星编队地面气浮台试验[78]

为了验证绳系编队动力学与初始状态之间的关系,Yu等[99]又在该试验台上对长绳系编队系统(LSTF)动力学进行了分析,讨论了LTSF的三种典型面内运动以及面外运动抑制,给出了三种运动形式的摆状振荡、旋转运动和不规则运动。图12为LSTF旋转运动轨迹仿真,可以看出,地面试验模拟器轨迹与卫星轨迹基本保持一致,验证了地面等效试验的准确性。

图12 LSTF旋转运动轨迹[99]

3.2 机构测试法

为了验证绳系系统释放、制动和回收等试验机构的可靠性,研究人员提出了机构测试法,主要是通过一些特殊设计的机构来测试绳系系统内部装置的特性。这些机构相对整个系统而言质量较小,受重力影响较低,因此在使用该方法进行相关模拟实验和可靠性验证时,对微重力环境的要求较低。

易琳等[100]研究了用于空间捕获的绳网收口方式,介绍了一种由双转子电机、双卷筒和自由导绳套筒组成的自适应系绳卷取机构。该机构能适应负载不平衡变化,不会发生系绳缠绕现象,具有较强的自适应性。Schultz等[101]为模拟Tips试验[102]中系绳内部张力变化的情况,采取控制系绳水平位移,使系绳只在竖直方向上移动的结构,利用摆锤来提供可变张力,如图13所示。通过选取合适的映射关系,分析系绳在试验中的内部张力情况可以研究在轨任务中系绳的内部张力情况。

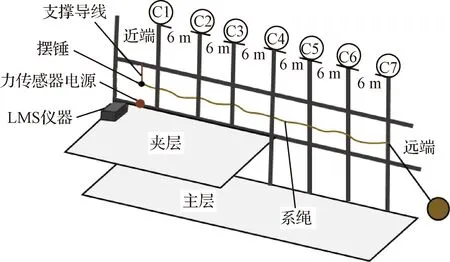
图13 绳系卫星水平结构配置地面测试装置示意图[101]

Nakamura等[103]开发了能够展开和回收微型卫星的微型系绳缠绕机构(MTRM)。它由一个卷轴、一个驱动电机和一个平风机构组成,包括一根2 km长的系绳,可控制卷轴电机扭矩以避免系绳松弛。此外在该机构基础上搭建了一个名为“绳系动力学模拟器”(TDSM)的地面试验系统。利用该模拟器对双体绳系编队进行了地面试验,用于验证该机构对系绳展开和回收的可靠性和有效性。试验最终成功将系绳展开至2 km。但在回收阶段,振动角在最后100 m发散。

3.3 失重飞机飞行法

除了以上提到的试验装置外,另一种通过飞机抛物线飞行构造微重力环境的方案也被一些学者应用于绳系系统的试验验证。其原理是飞机通过先爬升再迅速向下俯冲进行飞行的过程可以营造时间约几十秒10-2～10-3g左右的失重环境,可以用于精度较高的三维空间微重力实验模拟,但这种方法成本高昂,而且实验周期较短,目前仅有少数学者进行了失重飞机环境试验测试。

Benvenuto等[104]设计了一种可装载在失重飞机上的系绳展开试验装置,该装置主要由两颗立方体卫星结构组成,卫星结构内部附有系绳展开机构、高速摄像测量模块和数据存储模块。在完成展开控制律的地面试验验证后,Benvenuto等将该装置装在飞机上,在失重环境下进行试验。Zhu等[105]通过空气轴承转台和微重力抛物线飞行试验,对为微重力环境中的绳系立方体卫星展开进行了试验验证。绳系立方体卫星任务包括两颗1U立方体星,100 m长的带状系绳。系绳通过拉动展开,两颗立方体以期望的速度分离。该试验进行了各种地面测试,以验证设计的分离速度、估计内部摩擦力和测量展开的系绳长度。最后,通过微重力抛物线飞行试验验证了绳系系统展开的工程模型。试验过程如图14所示。

图14 抛物线飞行下的系绳展开试验[105]

该试验给出了两个立方体卫星之间相对距离的实测时间历程,如图15所示。可以看出,立方体卫星在自由飞行状态下的相对分离距离轨迹几乎是一条线性直线。虚线表示自由飞行状态下的相对分离速度,为1.42 m/s,高于地面试验测得的1.23 m/s的速度。试验结果证明了绳系系统在微重力环境中的内摩擦力小于在重力环境中测量的内摩擦力,验证了所设计的绳系系统的有效性,为后续的试验提供了很好的理论参考价值。

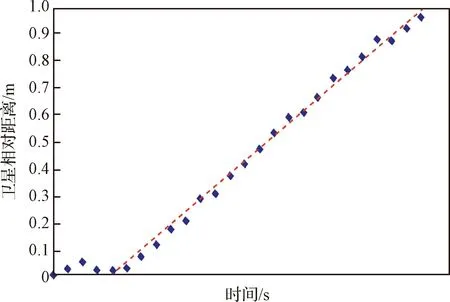
图15 卫星相对距离和分离速度[105]

地面试验是在进行昂贵、耗时的航天试验之前,验证绳系系统动力学和控制理论研究的重要工具。表2比较了几种地面模拟试验方法特点。可以看出,在已经进行的地面仿真试验研究中,气浮平台法和机构测试法由于造价低、设备维护简单等优点,已经被诸多学者用于绳系系统地面试验验证,但气浮平台只能在系统层面通过极低的摩擦力来模拟失重环境,无法为系统中的每一个结构进行失重模拟。通过气浮平台实现三维空间的复杂运动的实验较为困难,主要用于二维平面的飞行器模拟试验。而机构测试法仅适用于一些简单的内部机构可靠性验证,无法进行高精度的模拟试验。失重飞机试验虽然可以实现对微重力环境的高精度模拟,但由于设备造价及维护成本高昂,试验条件极为苛刻,且单次实验的微重力实验时间较短,对飞行器的各种设备性能指标无法全面考核,目前已开展的相关实验较少。

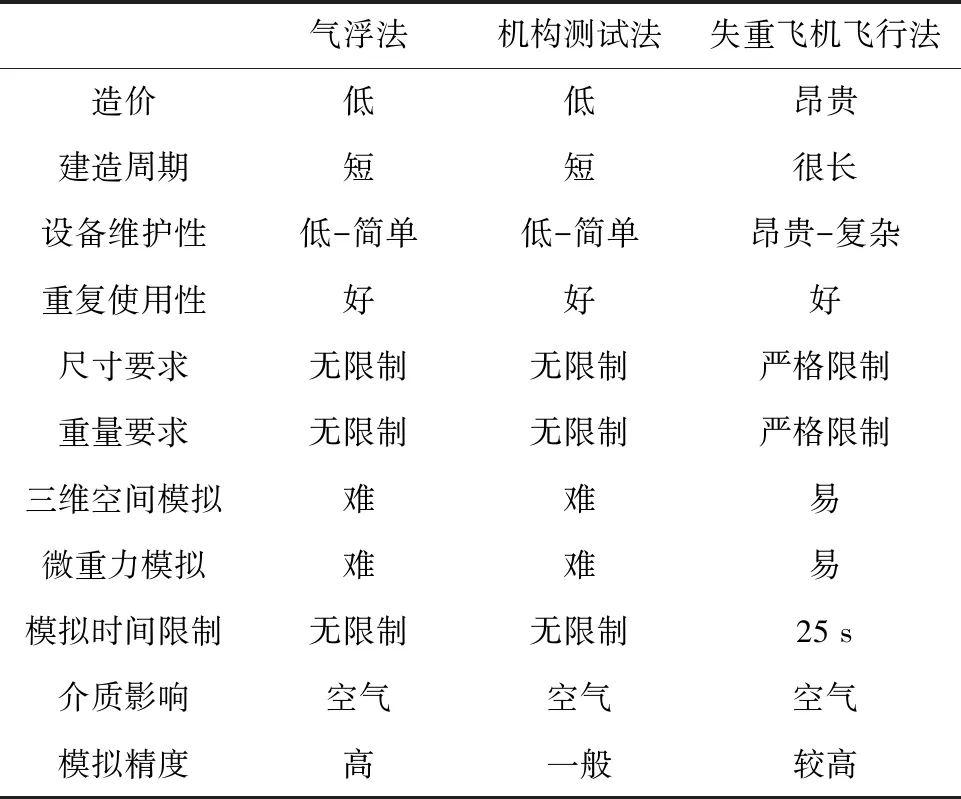
表2 各种地面模拟试验方法对比

4 结束语

空间多体绳系编队研究的快速发展将促进太空探索和开发技术的进步。本文首先简要介绍了空间多体绳系编队的构型,并总结了国内外研究学者对绳系编队动力学建模与控制、地面试验方面的研究成果。可以看出,作为一种新型的空间编队技术,绳系编队已经吸引了越来越多的关注,并且已经取得了很多研究成果,但仍存在一些不足,未来应从这几个方面开展进一步的研究。

1) 目前关于绳系编队动力学建模方面,针对诸如J2摄动、热效应、大气阻力以及太阳光压等空间环境外部因素的扰动,已经积累了很多研究。但在编队星体姿态的研究上,大部分系统建模均将星体考虑为质点,忽略了星体姿态的影响,仅有少量文献考虑到母星的姿态运动,但仍忽略了子星姿态。另外关于进一步考虑系绳与星体运动之间的耦合、系统姿态与轨道之间耦合的研究则更加稀少。因此,考虑绳系编队系统耦合关系的动力学建模分析将是未来研究的重点。

2) 空间多体绳系编队作为一种节省能量的编队构成方式,缺乏基于能量分析和对比方面的文献研究,未来需要更多从能量角度考虑的研究,例如与无绳系卫星编队的能量消耗对比,说明绳系编队在能量节省方面的可靠性。

3) 在现有的空间多体绳系编队星体姿态研究中,大部分文献没有考虑星体姿态机动的局限性,针对绳系编队星体姿态运动的限制范围分析,值得更加深入的研究。

4) 在编队构型研究上,目前大多文献仅针对某一种特定构型绳系编队进行控制,几乎没有考虑绳系编队在不同构型之间进行切换的研究。编队重构控制将是未来绳系编队研究的难点与重点。

5) 以往关于绳系编队的地面试验主要集中于结构较为简单的直链式或三角形绳系编队,没有针对空间构型绳系编队的地面试验研究。为了对绳系编队系统的可行性、可靠性等做更加深入的研究,复杂结构绳系编队的地面试验将是未来的研究重点。

6) 目前已开展的地面试验装置大部分还是以气浮台的方式进行研究,无法真正模拟太空失重环境。而失重飞机飞行法成本过高,维护周期太长。因此,未来可考虑建立更多微重力环境下的试验,例如可利用水下环境或真空罐进行试验装置搭建,目前在绳系系统领域还没有这方面的研究。