一种弹间协同的目标察打时间可调制导方法
武 建,赵 斌,韩 拓
(1. 中国电子科技集团公司第二十研究所,西安 710068;2. 西北工业大学精确制导与控制研究所,西安 710072;3. 北京航空航天大学航空科学与工程学院,北京 100191)
0 引 言
多弹集群协同组网形成编队饱和攻击模式,由于具备密集阵饱和杀伤、弹间数据链协同共享、目标察打能力提升等优势,成为突破重要目标多层防御网的重要手段。其中,针对集群协同饱和攻击的末制导律设计方法,是保证集群协同察打目标的关键核心,具有重要研究价值,且近年来发展迅速[1]。需要指出,比例制导由于具备高效、简单、实用等特性,自20世纪60年代以来,得到了广泛应用[2-4]。然而,在面对攻击时间约束、传感偏差或失效、导引头量测偏差、目标机动信息难获取等复杂工况下的饱和攻击问题时,传统比例制导具有一定保守性,难以同时解决以上问题,因此,需要开展适用于多弹集群协同饱和攻击的时间约束制导方法研究。
为了提升导弹集群饱和攻击制导性能与鲁棒特性,针对攻击时间一致收敛或攻击时间约束末制导律设计问题,文献[5]基于一致性理论和扩张状态观测器理论,设计了分布式一体化协同制导与控制律,并对闭环系统的稳定性和收敛特性进行了严格分析。文献[6]针对多弹从期望方向同时命中移动目标的问题,提出一种有向通信拓扑下无需弹目径向速度且带视线角约束的分布式有限时间协同制导律。文献[7]在突防器作为引诱角色的情况下,基于有限时间控制理论提出了一种带有拦截角约束的协同制导方法。上述协同一致趋近制导方法的优点在于保证多弹同时攻击目标的过程中不需要对具体攻击时间进行约束。在考虑攻击时间约束可调制导律设计方面,文献[8]基于比例制导与攻击时间偏差反馈项,针对线性化制导模型设计了次优反馈控制的攻击时间约束制导律。文献[9]将攻击时间制导问题转化为针对弹目距离跟踪的问题,基于反馈线性化与极点配置方法设计了攻击时间约束制导律。文献[10]为了克服制导模型线性化的保守性,提出了基于李雅普诺夫函数的二维和三维攻击时间约束制导律,并分析了制导律的奇异问题。在考虑速度时变的情况下,文献[11]通过设计并求解前置角参考剖面,给出了一种自适应攻击时间约束制导律。通过建立基于时间的高阶相对距离参考剖面,文献[12]提出了一种广义相对距离成型的攻击时间约束制导律。通过求解期望前置角的圆弧几何方程,文献[13]提出了基于双虚拟目标的攻击时间约束制导律。基于三维最优比例制导与攻击时间偏差反馈项,文献[14]提出了一种广义最优三维攻击时间约束制导律。文献[15]通过设计基于前置角跟踪误差的滑模面,设计了非奇异攻击时间约束制导律,并将其推广至拦截移动目标的场景中。文献[16]针对不同飞行段特点及任务需求,分别设计了各段导引律,推导了滑翔段飞行剩余时间和剩余航程的解析解。文献[17]设计了一种基于时间的二次多项式作为视线转率参考剖面,提出了针对不同运动目标的攻击时间滑模制导律。在给定初始条件与目标位置的情况下,文献[18]基于数据驱动的方法给出了比例制导轨迹与剩余飞行时间估计的确定方法,并以此设计了基于剩余时间误差的攻击时间约束制导律。
上述多弹集群饱和攻击所采用的末制导方法在鲁棒性与有效性等方面取得了很好的理论与应用研究成果,具有饱和攻击能力的末制导方法设计仍然是一个开放性问题。一方面,传统制导方法在抑制目标机动等复杂扰动时,在制导参数选取方面具有一定保守性(如需要高增益或更新策略抑制强扰动)。另一方面,制导高增益往往会带来指令震颤或饱和现象,导致在降低增益与提升抗扰能力方面难以平衡的问题。此外,目标运动信息往往未知,用于先进制导算法的弹目相对信息(如相对距离)对于被动探测导引头难以直接获取,则需考虑多弹饱和攻击过程中对相对运动信息进行协同估计问题。
因此,针对目标机动、干扰偏差、被动探测的多弹饱和攻击目标察打任务,如何设计一种多弹协同估计与攻击时间约束可调的强抗扰末制导方法,获取弹目运动相对信息,实现复杂工况下对机动目标的饱和打击/拦截,克服低增益与鲁棒性差之间的强关联矛盾,且不需要复杂制导参数设计,是本文拟解决的关键问题。基于此,本文提出一种基于非线性增量式动态逆[19]的攻击时间可调强抗扰制导方法,采用制导模型增量形式推理分析,同时基于弹间数据链协同共享信息,对弹目运动信息进行协同估计并将其融合至制导算法,实现复杂工况下的目标察打时间可调制导系统的扰动降级与抗扰增强等目的。仿真结果表明,所设计方法能够有效解决多弹对目标察打任务中的信息估计与时间可调制导问题,且具有较强抗扰能力,最终完成复杂工况下多弹协同察打的饱和攻击任务。
1 问题描述
由于制导律的设计可以将三维空间分解为纵向与侧向两个方向平面,同时考虑到导弹拦截或打击的对象可能为静止或机动目标,因此,下面分别给出平面内针对静止目标与机动目标拦截几何关系与制导模型。
首先,针对二维平面内拦截/打击静止目标问题,给出相应几何关系如图1所示。以其中一个为例,M代表导弹,T代表目标。导弹速度为VM,并且垂直于侧向加速度AM。相应的角度φM,γ,λ分别表示前置角、弹道倾角、视线角,且有φM=γ-λ,r为弹目相对距离,导弹与目标在x-o-y坐标内的位置分别记为(xM,yM)和(xT,yT)。基于图1几何关系,给出针对静止目标的二维制导模型如下

图1 二维平面内静止目标制导几何示意图
(1)
(2)
(3)
(4)
其次,针对二维平面内拦截机动目标的问题,给出相应的几何关系如图2所示。其中,目标速度与侧向加速度分别为VT和AT,目标弹道倾角为γT。基于图2几何关系,给出针对机动目标的相对运动方程可表示如下

图2 二维平面内机动目标制导几何示意图
(5)
(6)
目标的运动模型可表示为
(7)
(8)
本文考虑的制导问题为设计攻击时间可调的制导方法,同时基于弹间数据链协同共享方位信息,对弹目相对运动信息进行协同估计,为制导算法提供可用信息,从而实现复杂工况下的目标察打时间可调多弹饱和攻击任务。所谓攻击时间约束,即导弹以期望的时间命中目标,飞行时间可根据任务进行调节。考虑装配被动导引头仅可测角的情况,为了制导算法的工程实现,还需要实时估计弹目相对距离。因此,目标察打时间可调制导律设计问题可分解为两个方面:1)攻击时间可调强抗扰制导律设计;2)弹间数据链协同共享的弹目相对距离估计。
2 时间可调制导律设计
制导律设计途径之一是通过视线角速率动态方程开展的,因此,考虑制导模型及拦截几何关系,基于式至式给出视线角二阶动力学方程为
针对机动目标:
(9)
针对静止目标:
(10)
需要指出,直接基于上述视线转率动态方程设计零化视线角速率的制导律,不具备攻击时间调节能力,因为视线转率连续衰减到零的过程难以调节弹道曲率发生较大变化。下文将引入攻击时间可调的视线角参考剖面成型方法,给出攻击时间调节参数选取机制。
2.1 时间可调视线参考剖面设计
一般情况下,设计者可以列举出不同种类的视线角参考剖面,为了应用简便,同时受到文献[17]的启示,本文选取一种基于飞行时间的三阶多项式作为视线角速率参考剖面,如下所示
(11)

(12)

结合式(11)和式(12)可得
(13)
进一步可得
(14)
将式(13)和式(14)中δ2,δ3表达式代入式(11)可得
(15)
则视线角参考剖面可以通过对式(15)进行积分得到
(16)
式中:δ4为待确定常值参数。定义初始时刻导弹观测目标的视线角为λ0,则取te=t0=0时,可基于式给出视线角初始条件如下
λd(te=t0=0)=δ4=λ0
(17)
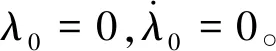

图3 不同δ1相同Td的参考剖面示例
可以看出,在同一攻击时间约束下,能够满足边界条件的参考剖面具有多种形式,在同一剖面调节参数δ1取值下,能够满足不同攻击时间约束的参考剖面也具有多种形式。此外,视线角速率在终端时刻为零的特性,隐含了基于视线角速率生成的制导指令可最终收敛到零的情况。
需要指出,本文所设计的三阶多项式视线角速率参考剖面,与文献[17]中二阶多项式剖面相比,其产生的制导指令初值表现为导航比为2的比例制导初值,且与剖面调节参数的选取、期望飞行时间约束、初始前置角大小均无关,该特性不仅放宽了对初始和终端条件的要求,同时一定程度可以避免文献[17]中不合理调节参数可能带来的初始制导指令过大甚至饱和问题。具体分析如下:以静止目标为例,基于式可知,在期望参考剖面的作用下,制导指令具有如下形式:
(18)
在te=0时,初始制导指令可写为
(19)
式中:下标“0”特指各物理量在初始时刻对应的取值。由于本文三阶多项式参考剖面的形式为
(20)
文献[17]的二阶多项式参考剖面对应的形式为
(21)
因此,本文三阶多项式参考剖面对应的初值为
(22)
文献[17]的二阶多项式参考剖面对应的初值为
(23)
进一步可知,本文三阶多项式剖面作用下的初始制导指令为
(24)
相应地,文献[17]二阶多项式剖面作用下的初始制导指令为
(25)
显然,与文献[17]中二阶多项式剖面相比,本文针对静止目标产生的制导指令初值表现为导航比为2的比例制导初值,且与剖面调节参数的选取、期望飞行时间约束、初始前置角大小均无关。
2.2 视线剖面跟踪制导律设计

(26)
针对静止目标,将式(10)代入式(26)可得
(27)
显然,可以将其改写为如下形式
(28)
式中:f与g分别为
(29)
(30)
针对式(28)可设计使α收敛的制导律为
AM=(f+pα)/g
(31)
式中:p>0为待设计的制导增益。
将式(31)代入式(28)可得
(32)
(33)
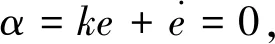
针对机动目标,将式(9)代入式(26)可得
(34)
类似地,可以将其改写为如下形式
(35)
式中:f和g的表达形式与式中表达形式相同,d=ATcosφT/r为目标机动带来的扰动。由于目标机动能力受限,则可假设d是有界的。
为了抑制目标机动带来的扰动未知项,针对式(35)可设计使得α收敛的制导律为
AM=(f+q·sgn(α))/g
(36)
式中:q>0为待设计的制导增益。
将式(36)代入式(35)可得
(37)
(38)
显然,当选择制导增益q满足q>|d|时,则可以保证α能够收敛,实现参考视线剖面的精稳跟踪。
2.3 扰动降级的增量式制导律设计
需要指出,针对机动目标的制导系统收敛特性和抗扰能力,与q和d的大小密切相关。由于难以预估d的大小,实际选取固定增益q时具有一定盲目性,在相同的增益q下,扰动d越大,会导致制导精度与抗扰能力降低。反之,相同的扰动d情况下,q越大,制导精度越高、抗扰能力越强。然而,较大的增益带来的可能会带来制导指令饱和或抖振现象。因此,如何在降低制导增益的同时,仍然能够增强攻击时间可调制导系统的抗扰能力,是本文期望解决的问题。受增量式控制理论及其制导律应用[19-20]启发,对式求近似泰勒展开式如下
(39)
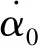
类似地,基于式(39)可给出增量式制导律
(40)
以及完整的增量式制导律表征形式
AM=AM0+ΔAM
(41)
其中,增量式制导律的增益参数qi>0。
将式(40)代入式(39)可得
(42)
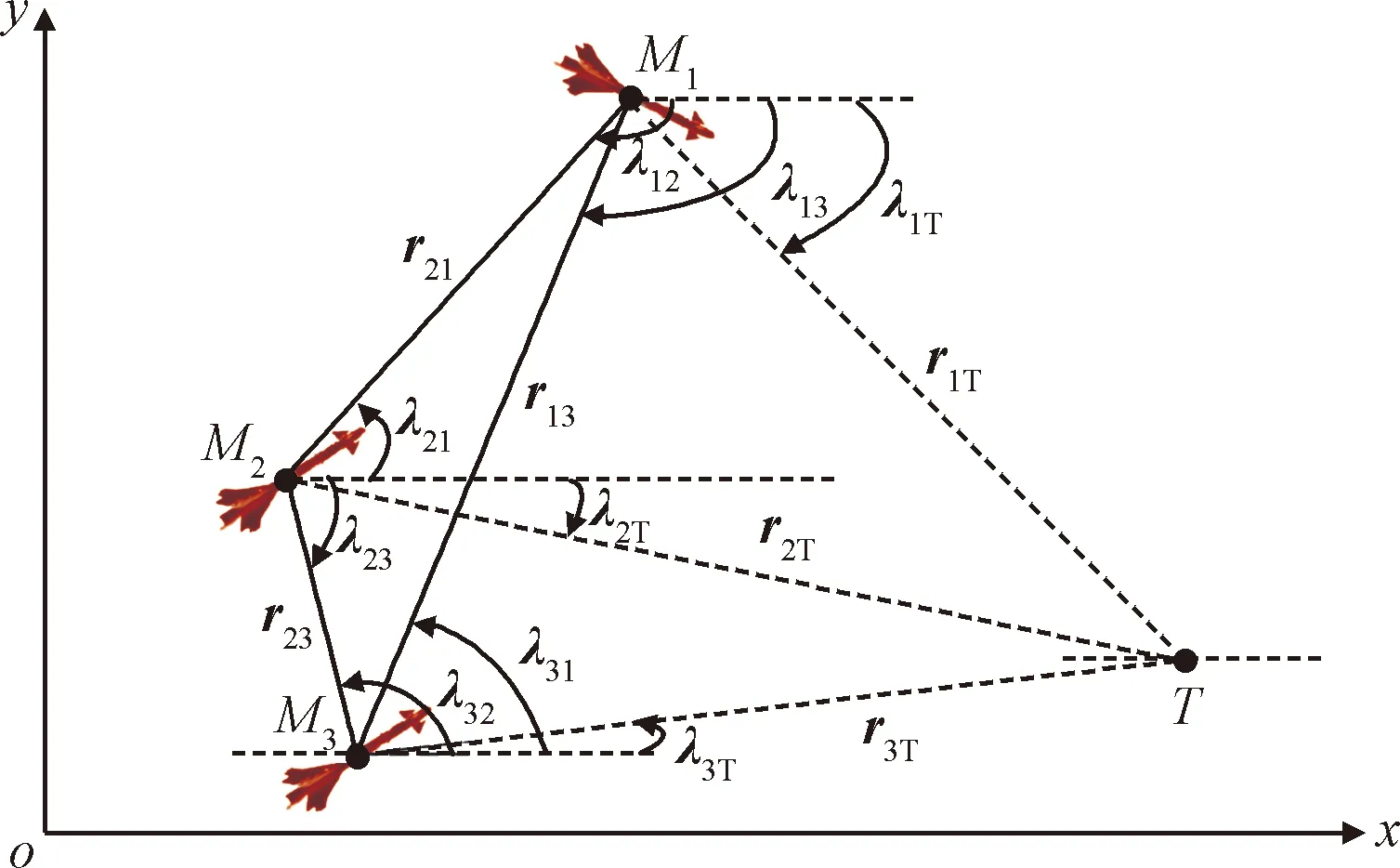
需要指出,目标机动在一个步长内的变化往往较小,因此,存在采样步长使得Δd 前述制导律的实际应用需要用到弹目相对视线角、视线角速率、相对距离等制导信息,其中,弹目相对距离对于装配被动探测型导引头的导弹无法直接获取,一般可通过导弹自身机动提升观测能力并结合滤波方法估计间接得到,或通过多弹方位共享协同几何测量估计得到[21]。针对本文研究的集群协同攻击任务,为了充分利用多弹之间数据链协同共享资源信息(如图5所示),基于弹间数据链协同共享的视线方位和位置等信息,对弹目相对距离进行协同测量估计,为制导算法的相对距离信息获取提供可用信息。其中,弹间协同共享方位等来自多弹集群数据链组网信息,λij(i=1,2,3,j=1,2,3,T)表示弹间视线测量角或导弹对目标的实现测量角。为了快速在线求解每个导弹与目标之间的相对距离信息,考虑到弹间数据链组网共享且彼此已知位置信息,则弹间距离已知。定义弹间协同共享的相对距离为rij(i=1,2,3,j=1,2,3),则基于图5所示弹间视线方位协同共享机制,获取弹目距离信息如下所示[21] 图5 弹间视线方位协同共享 (43) 进一步,将上述关系递推至n个导弹组成的集群网络中,可得第k个导弹与k之外n-1个导弹(定义为m)对协同测量相对距离实时估计形式为 m,k=1,2,3,…,m≠k (44) 根据文献[21]可知,弹间视线分离角是决定弹目距离协同获取精度的重要影响因素。两个导弹(导弹i和导弹j)间的视线分离角可定义为 λfij=λiT-λjT i=1,2,3,…,j=1,2,3,…,i≠j (45) 当协同探测存在噪声和不确定时,|λfij|越大则估计误差越小[21]。基于此,可调节|λfl|提升估计特性,即调节λfij(t=Td)大小(定义满足估计特性要求的最小分离角为λr)。结合2.1小节内容,对于时间可调察打制导的导弹i和j来说,分离角λfij可表示为 (46) 进一步,可得 (47) 式中:δ1jj=δ1jT-δ1iT表示弹间协同剖面可调分离参数;ρ1,ρ2为已知系数,则弹间协同估计的弹目距离信息获取特性提升的约束条件可转化为对δ1jj有效集的求解问题,即 {δ1jj|ρ1δ1jj+ρ2<-λr}∪{δ1jj|ρ1δ1jj+ρ2>λr} (48) 因此,通过求解分离参数有效区间,可给出满足一定分离角约束的察打构型,在提升对相对距离可观测性能的同时,实现多弹集群协同察打任务。 注1.基于不等式可知,提升观测性能的分离角约束给剖面调节参数带来了范围限制。根据文献[17],不同调节参数限制范围将对飞行时间的调节产生影响,较大的参数调节范围往往能够调节更加宽域的飞行时间,但最终仍受限于自身物理特性。同时,由于分离角约束为固有预设属性,弹目距离估计特性要求越高,飞行剖面调节参数可行范围越窄,对应的飞行时间一致协同可达域越小。对于物理条件限制下的飞行时间可达域求解问题,参考文献[17]给出了一种数值方法,较为容易通过在线数值求解得到,在此不再赘述。 为了验证所设计方法的有效性,选取文献[17]的目标模型以及导弹物理参数作为基准开展仿真验证。目标运动形式分别选取为静止和正弦机动形式。制导律与的制导增益参数分别选取为q=3,qi=0.1。同时,选取导航比为3的比例制导律作为参考。为了表示方便,将本文时间可调传统鲁棒制导律与增量制导律分别表示为CG和ZG,将比例制导律表示为PNG。仿真初始位置、弹道倾角、导弹速度等参数设置如表1所示,考虑三枚导弹协同察打机动目标可调时间约束为50 s,目标为海面航行的快速舰艇,速度为30 m/s,且具有侧向机动能力,给出仿真结果如图6~9所示。 表1 仿真初始设置 图6 协同察打机动目标飞行轨迹 可以看出,所设计制导律能够使得三枚导弹对飞行弹道曲率进行调整,以满足期望的察打时间,在既定时间同时攻击目标,从而实现集群饱和攻击任务。然而,传统比例制导律由于采取了视线转率快速收敛为零的策略,难以对自身弹道进行在线调整,从而无法满足期望察打时间约束。通过图7的制导指令可以看出,为了对弹道曲率进行重塑,目标察打时间可调制导律在期望的视线转率剖面作用下,产生了相应的制导机动指令。图8所示的视线角变化趋势也表明,传统比例制导对视线剖面无重塑作用,且不同初始位置和方向启控的导弹难以协调飞行时间来满足协同打击任务需求。 图7 协同察打机动目标制导指令 图8 协同察打机动目标视线角变化 针对传统扰动抑制制导律和增量式制导律的视线剖面跟踪能力分析,图9给出了两种制导律作用下的视线角跟踪误差变化特性。可以看出,CG制导律在整个末制导目标察打过程中,视线角跟踪误差均未严格归零,且在命中目标点附近存在较大误差。这是由于在拦截机动目标过程中,命中点附近存在视线转率突变的情况,CG制导律预先设置的制导参数难以对较大扰动进行抑制,从而导致较大误差。然而,增量式制导律由于回采了实时系统状态信息,且对扰动进行了降级处理,整个末制导过程均保持了几乎为零的视线跟踪误差特性。图10给出了三枚导弹协同察打过程中对弹目距离估计误差特性,可以看出,协同察打数据链方位共享的弹目距离协同估计误差较小,且最终收敛到零附近。进一步,针对不同目标察打时间调节约束,给出了察打时间分别为52 s、45 s的多弹协同察打飞行轨迹,如图11所示。综合来看,所设计的方法能够满足多种期望察打时间约束下的集群饱和攻击任务。 图9 协同察打机动目标视线角跟踪误差 图10 协同察打机动目标相对距离估计特性 图11 不同协同察打时间的飞行轨迹 1) 设计了具有终端约束的视线参考剖面,提出了一种扰动降级、抗扰增强的多弹协同察打时间可调制导律,并分析了制导收敛与鲁棒特性。 2) 针对弹间数据链协同方位共享的弹目距离信息获取问题,给出了保障协同估计观测特性的视线剖面调节分离参数有效集求解方法。 3) 复杂工况下仿真结果表明,所提出的方法能够提供弹间协同估计的弹目距离获取及多弹集群协同察打时间可调飞行任务。3 弹间方位协同的相对距离获取
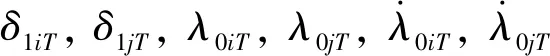
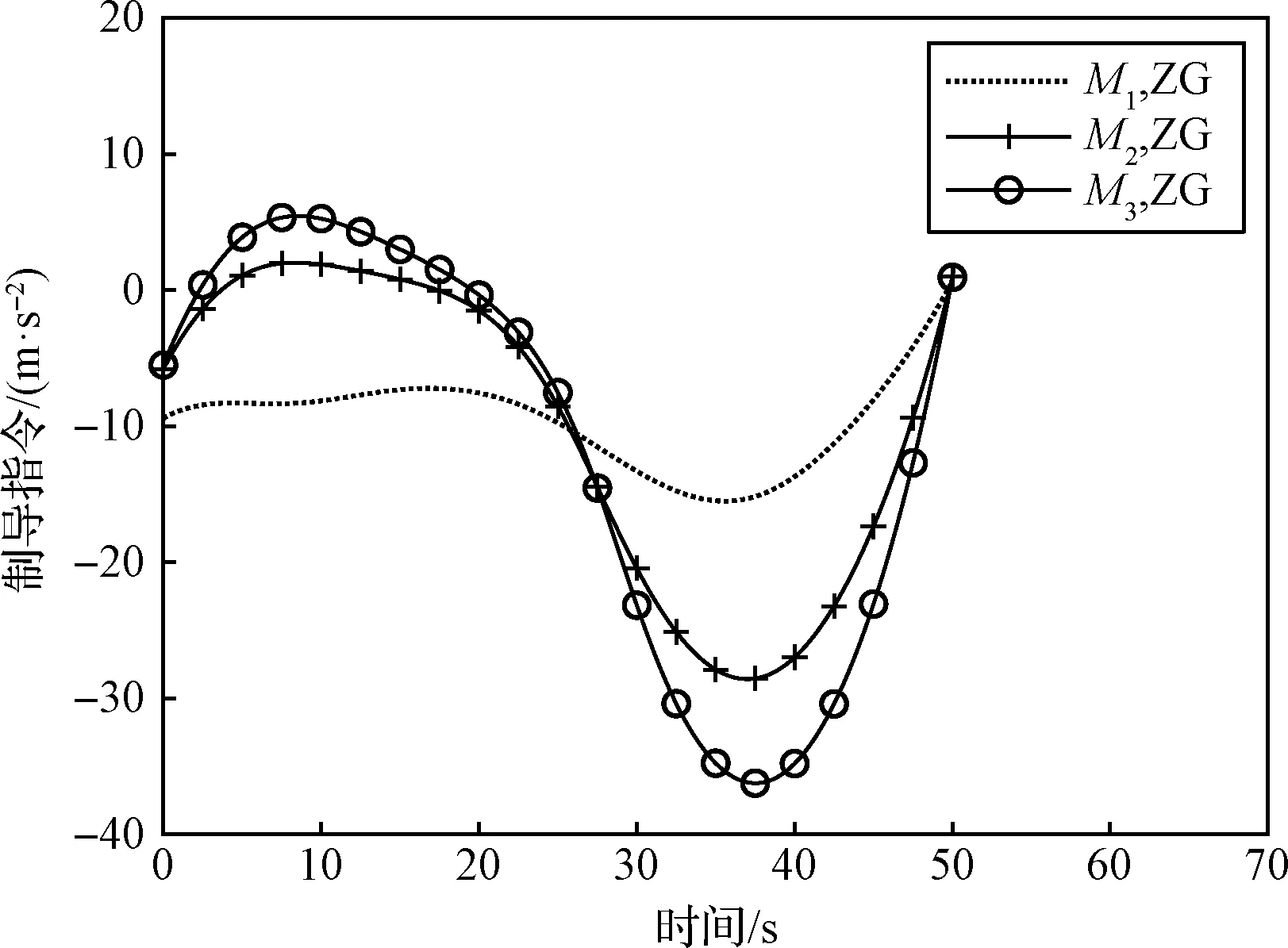
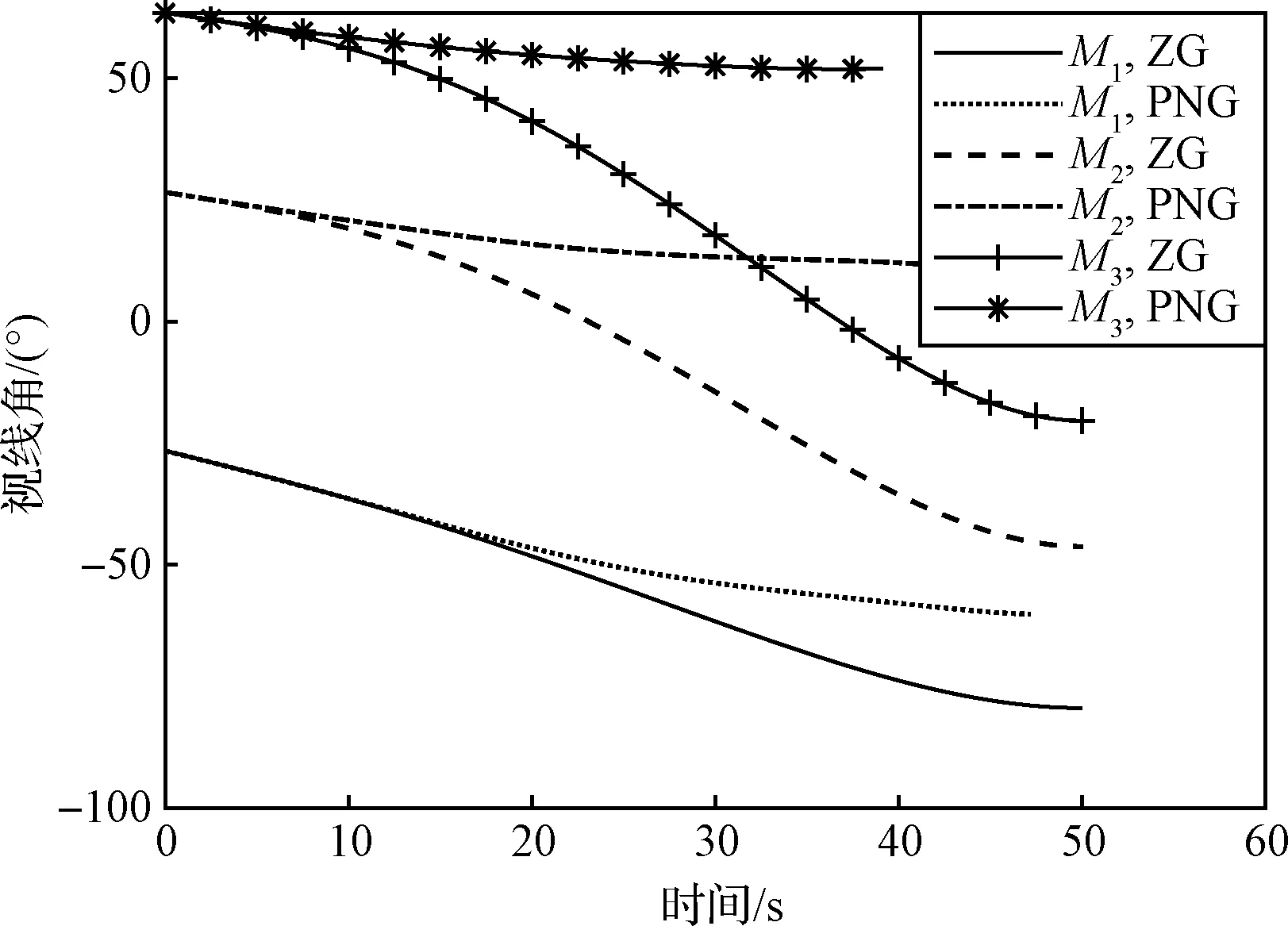
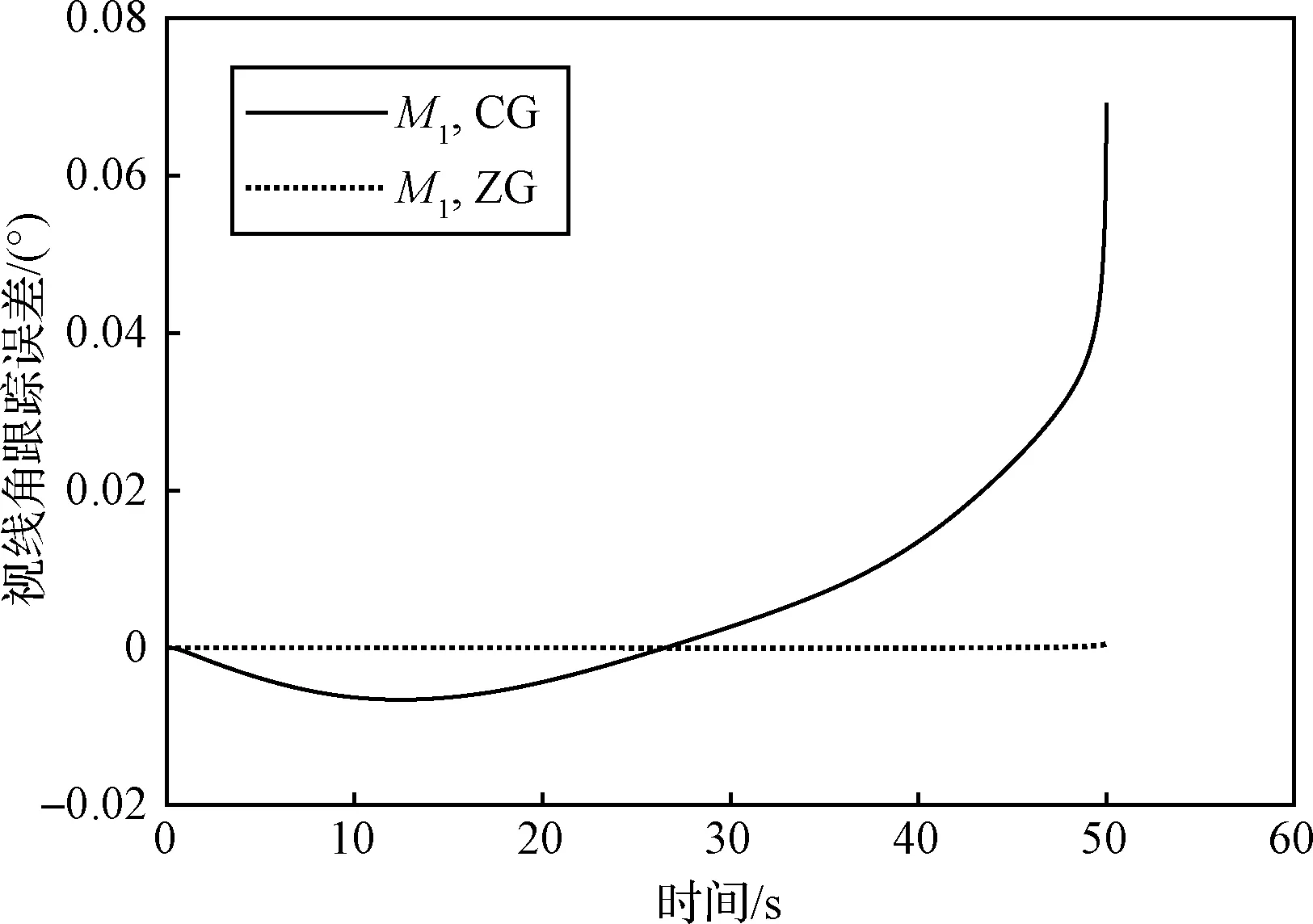
4 仿真校验




5 结 论

