考虑执行器最优分配的空间站舱内机器人位姿耦合控制

李鸣昊，王 辉，伍思欢，马 克，张锦绣

(中山大学航空航天学院，深圳 518107)

0 引 言

随着中国空间站梦天实验舱顺利完成转位,中国空间站建造任务即将完成收尾,在空间探索的方向上又向前迈出了一步。在这一背景下,航天员身心健康的问题需要被重点关注。在已有的空间站和空间实验室内,航天员承担了绝大多数的实验任务,较长时间的工作和较多的任务可能会给航天员带来一些身心负担,而空间站舱内机器人可以为航天员提供协助和陪伴,减轻他们的工作压力和心理压力。

自20世纪80年代以来,随着空间技术的发展,各国对于舱内机器人的研究也在不断推进。国外部分机构最早对舱内机器人展开了研究。如:NASA研制出一种个人辅助卫星[1](PSA),并在此基础上研发了携带机械臂的舱内机器人“宇航蜜蜂”[2-3](Astrobee);美国麻省理工大学研制了舱内同步定位、执行与重定向试验卫星(SPHERES),并进行了六自由度控制算法的实验[4];日本宇宙航空研究开发机构(JAXA)研制出一种可以辅助航天员拍摄照片的智子球形机器人[5](Int-ball)。以上国外的研究内容表明舱内机器人具有为航天员提供辅助的功能,具备作为空间站舱内扩展实验平台的能力,有较高的研究价值。

目前,国内也有不少研究团队对空间站舱内机器人开展了研究。刘金国等[6]设计了一种球形的舱内辅助机器人(AAR),并在其基础上改进设计了一种多面体外形的AAR2舱内机器人[7],还为其设计了快速稳定的六自由度控制算法;张琦等[8]设计了一种由多个推力器作为执行器的舱内机器人并验证了其空间站内的适用性;程瑞洲等[9]提出了一种面向在轨服务的人机交互方法,可为空间站舱内机器人扩展人机交互服务功能和提高舱内机器人的应用价值提供重要参考;岳程斐等[10]针对在轨工作机器人的三维路径规划问题提出了一种拓邻域蚁群搜索算法,并进一步提出一种用于多臂航天器的多层次路径规划方法[11-12],有效解决了多臂空间机器人的轨迹规划问题,对舱内机器人的工作轨迹规划方法研究有重要参考价值。

空间站舱内机器人六自由度灵活运动的特性决定了需要对其进行六自由度的位姿耦合动力学建模,以往有关舱内机器人研究中的动力学描述通常较为复杂,目前,许多学者采用对偶四元数进行六自由度运动空间系统的描述,可以极大简化空间六自由度系统动力学方程的复杂形式。王剑颖等[13]采用对偶四元数的方法建立了空间两航天器的追踪模型;马可锌等[14]基于对偶四元数给出了编队飞行卫星相对位姿的描述。

空间站舱内机器人优秀的辅助性能和运动特性需要有足够灵敏的控制算法作为支撑。对于此类机器人常见的控制算法有PID控制、模糊滑模控制、自适应控制等。刘金国等[6]设计了一种PID神经网络算法对舱内机器人进行姿态控制,并设计了一种模糊滑模控制方法[7]进行了空间站舱内机器人六自由度的控制;张琦等[8]采用具有二次函数型切换面的滑模控制的方法对舱内机器人设计了位姿一体化控制器;王辉等[15]针对气驱柔性臂空间站舱内机器人设计了一种无模型鲁棒跟踪控制器;张鑫等[16]针对携带臂体的舱内机器人设计了一种基于时延估计(time-delay estimation)的无模型解耦控制方法,解决了舱内机器人“基体-臂体”耦合问题并实现了二者的协调运动;陶东等[17]针对自由漂浮的服务机器人,提出一种考虑模型不确定情况下的无力传感器阻抗控制方法,并通过数值仿真验证其可以在保证控制精度的情况下降低空间服务机器人动力学建模精度要求,提高了工程可行性。围绕空间站舱内机器人的控制问题,很多学者已经开展了深入的研究。然而,空间站舱内机器人执行器的冗余特性以及考虑执行器最优分配的位姿耦合控制方法仍是工程化过程中亟需解决的问题。

因此,本文针对空间站舱内机器人考虑执行器分配的位姿耦合控制问题,首先建立舱内机器人相对于空间站平移与旋转的统一性的描述,解决了以往有关舱内机器人研究中的动力学描述通常较为复杂的问题;经过优选,确定一组具有均衡控制能力的最优冗余布局方案,并建立相应的执行器模型;在此基础上,设计考虑执行器最优分配的位姿耦合控制器,采用罚函数法对系统冗余的执行器构型进行力和力矩的分配优化。最后,经过仿真验证该方法的有效性。

1 舱内辅助机器人与空间站相对运动方程

1.1 坐标系定义

(1) 地心赤道惯性坐标系OI-XIYIZI该坐标系以地心为原点,OIXI轴沿着赤道面和黄道面的交线指向春分点,OIZI轴指向北极点,OIYI轴与它们构成右手螺旋。该坐标系用于描述空间站与机器人的运动方程。

(2) 空间站本体坐标系Ot-XtYtZt该坐标系以空间站质心为原点,OtXt轴与空间站过道平行,指向空间站前进方向,OtZt轴垂直于实验舱过道指向实验舱顶部,OtYt轴与它们构成右手螺旋。该坐标系作为参考系用于描述空间站舱内机器人在空间站舱内的相对运动状态。

(3) 机器人本体坐标系Ob-XbYbZb该坐标系以舱内辅助机器人质心为原点,ObXb轴平行于机器人底面指向机器人正面中心,ObZb轴垂直于机器人底面指向顶面中心,ObYb轴与它们构成右手螺旋。该坐标系作为本体系,与作为参考坐标系的空间站本体坐标系一同用于描述空间站舱内机器人在空间站舱内的相对运动状态。

1.2 基于对偶四元数描述的舱内辅助机器人相对动力学方程

(1)

式中:ε是对偶算子,表示Banach空间下与实数域垂直的某一维度单位向量,并且满足ε2=0。对偶四元数方程为

(2)

(3)

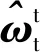
(4)

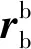
(5)

对偶四元数方程为

(6)

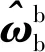
(7)

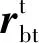
(8)

对式(7)求导,空间站本体坐标系下辅助机器人的对偶四元数方程可写为

(9)

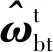
(10)

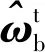
(11)

对相对速度旋量求导得:

(12)

代入动力学方程得:

(13)

式中:

(14)

(15)

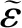
根据作用力的种类,本体系下的对偶力旋可以拆为

(16)

(17)

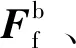
(18)

其中,阻力旋量可写为

(19)

由于舱内飞行机人姿态变换时转速较小,产生的气动阻力矩近乎为0,可认为τf=03×1,运动时的所受的气动阻力与运动速度相关。

(20)

式中:空间站舱内的空气密度ρ=1.27 kg/m3,v为舱内辅助机器人在各个方向上的瞬时速度矢量。将阻力分解至3个方向后,各方向的特征面均为正方形,特征面积记为S,其特征面长度记为d;CD为阻力系数。

(21)

1.3 舱内辅助机器人控制系统执行器布局优化

将舱内辅助机器人视为质量均匀分布的立方体,其上分布有若干作为控制器的微型风扇,微型风扇由无刷直流电机驱动,可以产生垂直于辅助机器人表面的一定大小的推力。

舱内辅助机器人的运动控制能力由微型风扇的个数、每个微型风扇的位置以及微型风扇所能产生的推力共同决定。二者的关系可表示为

Ur=Af

(22)

式中:Ur∈R6×1表示机器人本体受到的控制力与控制力矩在三维空间内各方向的分量。

Ur=[Tx,Ty,Tz,Fx,Fy,Fz]T

(23)

A=[A1(β1),A2(β2),…,An(βn)]

(24)

式中:{β1,β2,…,βn}表示推力器所在平面的位置。β的全部取值集合表示为

{β1,β2,…,βn}⊆{x+,y+,z+,x-,y-,z-}

(25)

对于1≤j≤n,j∈N,第j个风扇的推力配置向量[19]定义为

(26)

式中:{lxj,lyj,lzj}分别表示本体系下第j个风扇推力器中心距X,Y,Z轴的距离。此外,f=[f1,f2,…,fn]T表示实际推力大小。由控制力方程可知,当微型风扇的数目大于等于6,且每一风扇可以至少独立控制一个方向的控制力或者控制力矩时,冗余系统控制力与推力矩阵f不是一一映射的,且推力分配结果与装配矩阵和推力分配模式二者均相关。

为了使用最少的推力器得到最优控制效果,可以对装配矩阵进行优化。为保证式(22)解不为空集,至少使用6个风扇各自分布于机器人X,Y,Z3个方向处于正负轴两侧的面上。在此基础上将每3个风扇分为一组,各自加装在与X,Y,Z轴分别垂直的3个面上,比较增加后与增加前的结果。又因为在安装矩阵的后3项成比例时,风扇的位置越靠近边缘,在相同推力的条件下产生的力矩越大,可以起到节省能量的作用,因此在寻优的过程中考虑风扇都装在机器人的边缘处。由装配矩阵形式可知,当某一风扇位于过机器人质心的垂直于机器人表面的平面与机器人表面的交线上时,该风扇会产生非耦合力矩;反之,则该风扇会产生耦合力矩。图1至图2表示了给定每个风扇最大为1 N的推力时,两种装配方式的逆求解控制力范围。

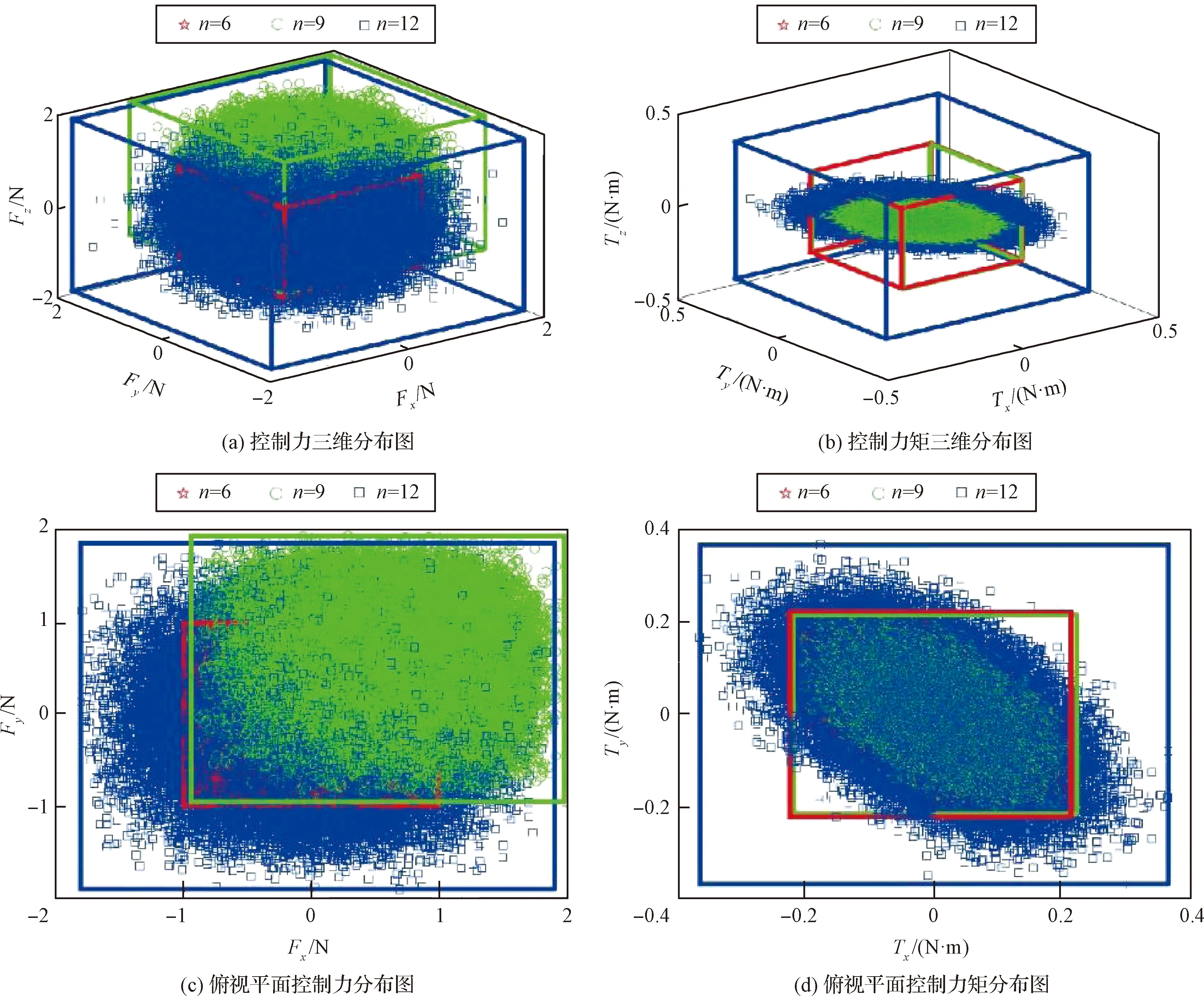
图1 力矩耦合式装配逆求解结果

图2 力矩非耦合式装配逆求解结果

表1 各装配方式评价函数值

由于空间站中各个方向外界条件相同,各个方向具有相同控制能力的控制器可以让舱内机器人拥有更多种运动形式。因此,将各个方向和各个面上控制能力均等作为约束条件,导出以下评价函数:

Θ=c(D(pfi)+D(pmi))

(27)

式中:pfi和pmi分别表示第i域内的概率;c为放大因子,取为100;D(·)表示方差。按照这一评价函数,Θ越小说明该装配矩阵下的控制能力越均匀。

根据评价函数计算结果,最终确定采用十二风扇推进的力矩非耦合式装配方案,其装配矩阵为

(28)

式中:d代表舱内辅助机器人每一特征面上几何长度的一半。这一装配矩阵的物理意义是每一个风扇均装在辅助机器人特征面对称线上的边缘处。风扇装配形式如图3所示。

图3 风扇装配示意图

2 基于对偶四元数的位姿耦合控制器设计

2.1 控制系统基本原理

对于该考虑执行器最优分配的空间站舱内机器人位姿耦合控制系统,基本架构[20]如图4所示。

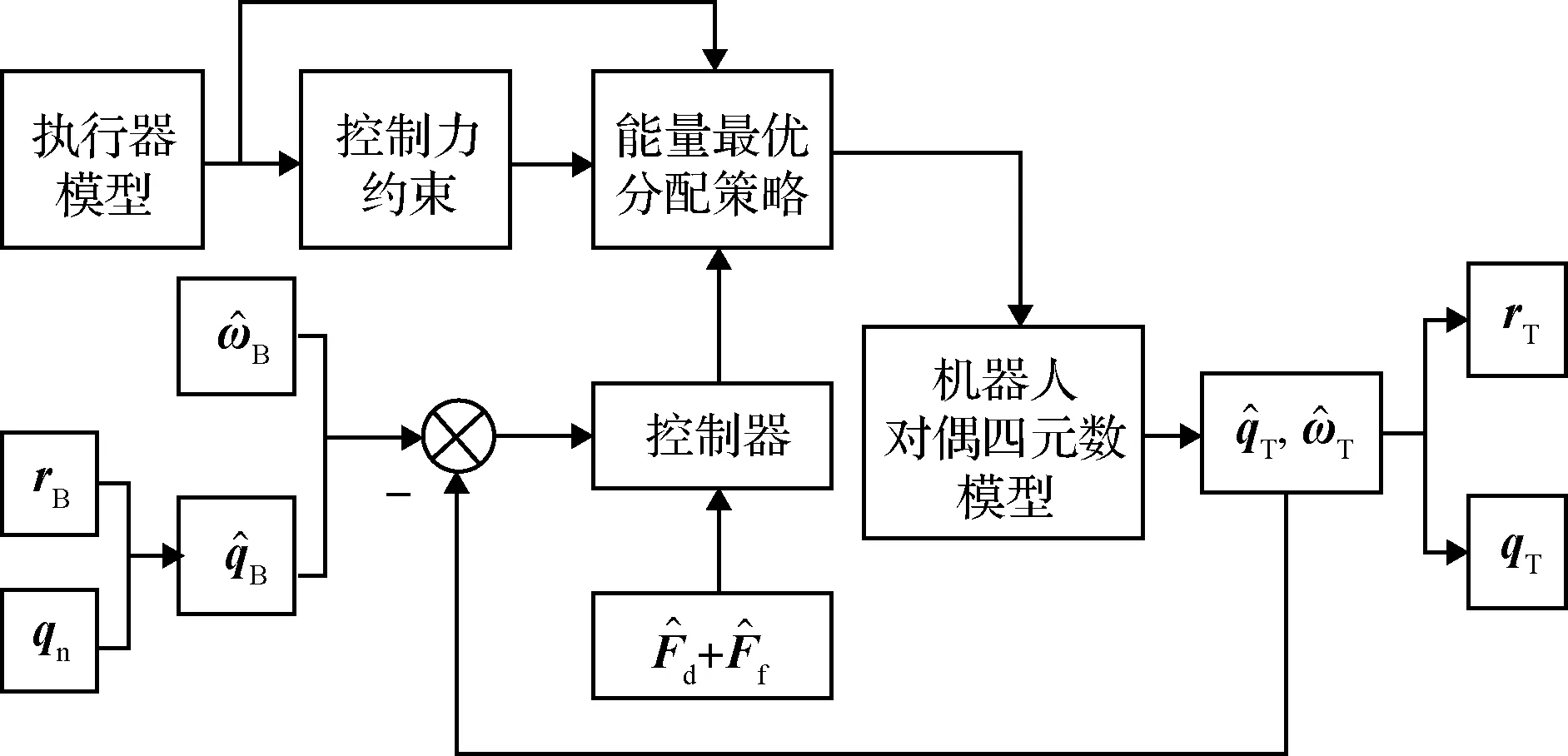
图4 控制与分配逻辑

首先,根据目标位置和姿态信息与初始位置和姿态信息得到目标状态的对偶四元数与初始状态的对偶四元数,以此获得对偶误差。再根据对偶误差与扰动力进一步获取控制力的,但此时控制力不一定能够满足执行器的物理限制,因此加入分配器作为分配力和给定执行器物理限制的约束,对控制力进行二次规划,进一步得到系统实际控制力,再由此实际控制力,根据舱内机器人的运动学与动力学方程得出机器人的当前对偶四元数,最后由当前对偶四元数可以解算出舱内机器人的实际位置、速度、姿态和姿态角速度信息。

2.2 控制器设计与稳定性验证

本节将对控制器和分配器进行设计,采用式(29)中的控制力作为控制器输入[21]：

(29)

(30)

kp与kd分别为控制器的比例系数与微分系数,它们具有对偶数形式:

(31)

(32)

定理1：对于式(9)与式(13)所描述的基于对偶四元数描述的位姿耦合空间站舱内机器人,采用式(29)中的控制力作为控制器输入[21]的控制系统是稳定的。

证明：基于李雅普诺夫稳定性定理,选择式(33)所示的李雅普诺夫函数[21],可通过证明其函数正定,且其导数负定,说明系统的渐近稳定性。

(33)

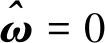
(34)

将式(13)代入式(34)后可得:

(35)

进一步可得:

(36)

通过消去反对称阵[21],该导数值最终可化简为

(37)

说明系统是渐近稳定的。也即引入式(29)所示的控制力后,由式(9)与式(13)确定的系统可以达到收敛。

2.3 基于内罚函数法寻优的力和力矩分配器模型

通过明确基于能量最优的评价函数,可以建立起基于该评价函数的执行器分配寻优方法。首先计算系统的能量损耗。按照以下方法建立微型风扇能耗计算模型[22]：微型风扇推力f与转速n之间的关系表示为

(38)

式中:D为扇叶直径;ρ为空气密度;KF为推力系数。式(38)中右边前3项在确定了推力器选型与工作环境后均不发生变化,可以设为常数LF：

(39)

电机转速与推力之间的关系可描述为

(40)

单个推力器的工作功率可描述为

(41)

式中:P是无刷电机功率;Tq是电机转矩;η是电机效率倒数。通过计算某一时刻构成空间站舱内机器人控制系统执行器的全部12个风扇的瞬时总功率引入功耗最小的价值评价函数:

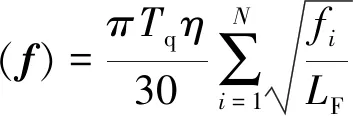
(42)

式中:fi表示第i个风扇的电机的推力;N为电机个数。系统总功耗是对整个工作时间内系统总功率进行积分得到的,因此,ϑ值越小,代表系统耗能越小,具备越高价值。

根据控制律得到控制力以后,分配力公式为不具有唯一解的冗余方程组。依据式(42)建立起的能量最优评价函数,进行式(22)所示线性方程组的最优解搜索,即可得到能量最优条件下的分配力结果[23]。该问题可描述为

(43)

其中,lb与ub是自变量的最小值和最大值。本例中约束由控制力与分配力的关系决定,其中控制力与分配力的关系如式(22)所示,其中安装矩阵形式已在式(28)中确定。由于微型风扇产生的最大推力不超过1 N,又因风扇无法产生负向的推力,故存在如下约束:

0≤fi≤1 N,i=1,2,…,12

(44)

寻优过程如下:

首先根据式(42)所示能量评价函数,建立内罚函数[24]：

(45)

进一步构建增广函数:

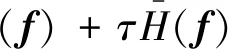
(46)

式中:τ为罚参数。

取可行域内的初始点f0=[f01f02…f012]T并在取定初始罚参数后继续求解无约束子问题:

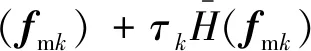
(47)

无约束子问题可采用牛顿迭代法进行求解。首先求解子问题中的增广函数H(f,τk+1)的Hessian矩阵Hk：

(48)

根据Hessian矩阵求解第k+1步的fk+1值:

(49)

当fk+1-fk满足精度要求时,即可停止迭代,得到无约束子问题的最小解fmk。求得子问题的最小解fmk后,根据式(50)所示的终止条件来进行进一步的判断:若该条件不成立,则令τk+1更新为ρkτk,重新计算minH(f,τk+1);若条件成立,则令fmk为近似最优解[25]。

(50)

按照这种方法,可以在有限时间内搜索得到满足式(42)所示耗能计算值最小的评价函数,并给出对应该评价函数的最优分配力。该分配力经过计算可以得到系统的实际控制力。

3 仿真校验

舱内机器人整体质量m=5 kg,特征面边长l=0.232 m,空间站运行轨道视为近圆轨道。舱内机器人含执行器在内的转动惯量设置为

(51)

研究系统在初始角速度ω0,初始欧拉角E0,初始速度v0与初始位置p0按下式设置,并在该初始条件下进行姿态回正。

(52)

控制参数设置为

(53)

空间站内由排气和人为引起的干扰气流流速[8]一般不会超过0.5 m/s,假设同时不会存在超过4股干扰气流,由于扰动气流的作用位置是随机的,气流扰动可以设置为随机大小的力螺旋,其大小限制根据式(20)可计算为

(54)

仿真时间步长选为0.1 s,分配寻优中的精度δ取为10-6,采用定步长四阶RK法作为求解方法进行仿真,仿真结果图5至图7所示。此外,分配结果将与去除式(42)所示评价函数但保留式(44)所示执行器限制条件随机取值的只考虑执行器性能随机分配结果进行对比,仿真对比结果如图8所示。

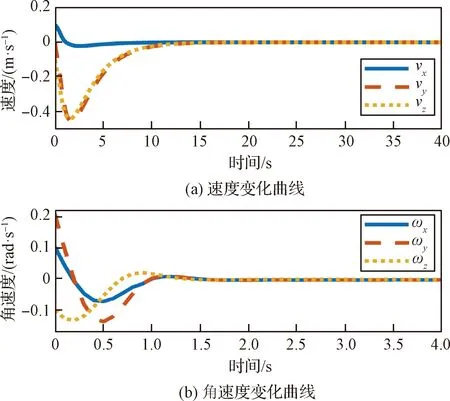
图5 速度与角速度变化仿真结果

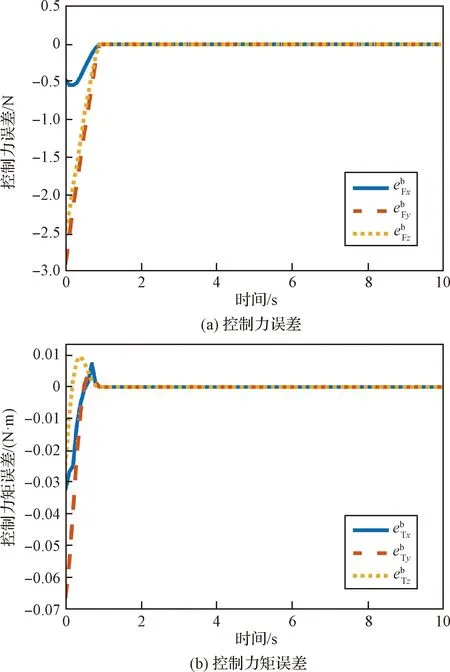
图7 控制力与控制力矩误差曲线

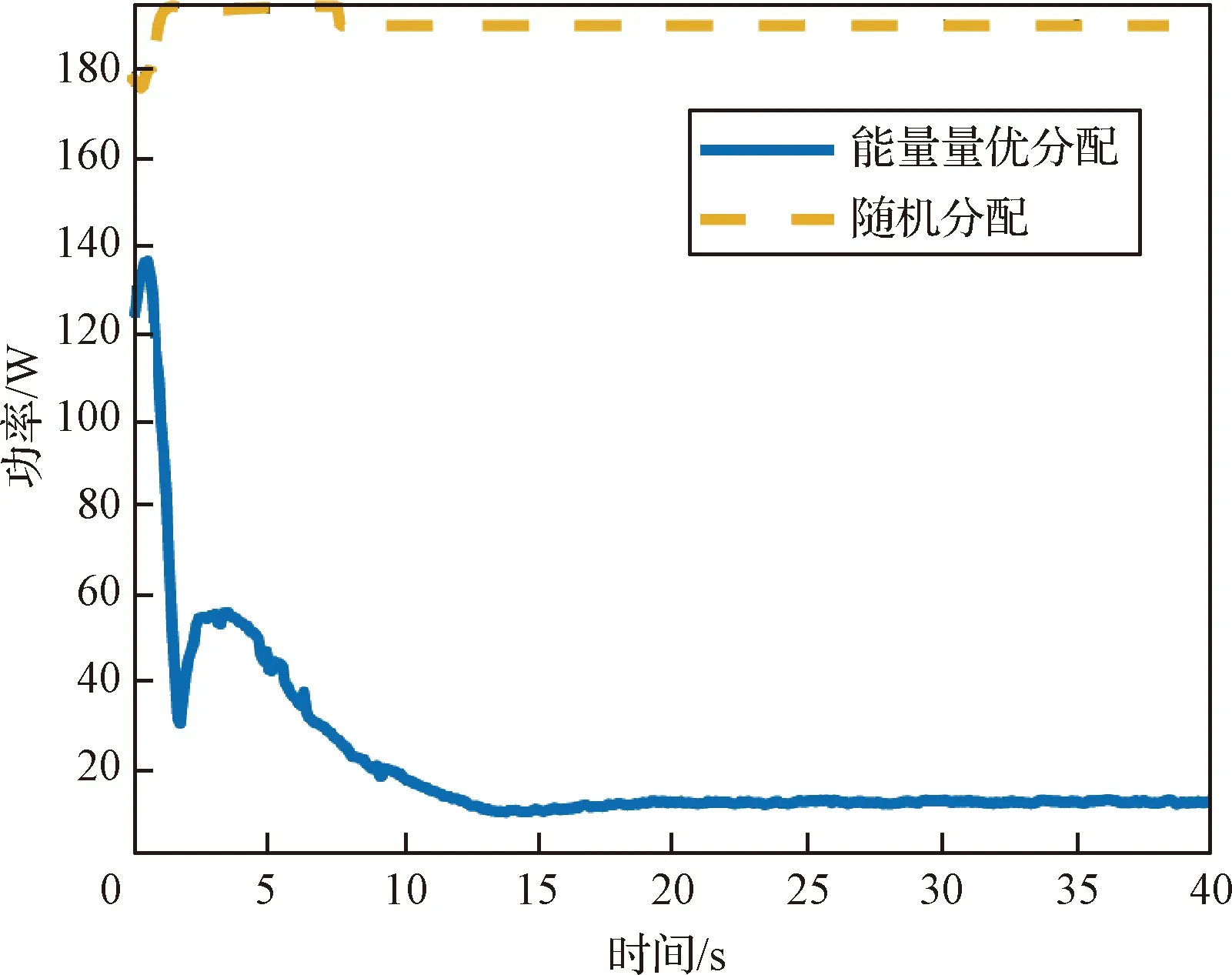
图8 加入分配器对执行器功率的影响

图5至图7中的结果表明,在控制器作用下,舱内机器人稳定时各方向的速度绝对误差小于5×10-4m/s;角速度绝对误差小于1×10-4rad/s;位置绝对误差小于5×10-3m;欧拉角绝对误差小于3×10-4rad。

推力分配的结果均满足式(43)所示约束,为验证该分配方式满足功耗最小的寻优目标,进一步考虑执行器功耗进行仿真。考虑风扇效率为0.9,空气密度为1.294 kg/m3。根据文献[22]简化的小风扇模型,在空气中的推力系数KF可按式(55)进行估算:

(55)

式中:Nf为小风扇扇叶数目;pf为小风扇螺距;Df为小风扇直径。取小风扇扇叶数目为6,螺距为10 mm,则推力系数KF可估算为0.000 87。由此,从执行器功率的角度验证分配器的性能。

图8表明,考虑执行器性能同时加入分配器后,该控制器仿真中功率大幅加降低。这是由于加入分配器后,根据能量最优策略执行器会寻找能耗较小的分配方案进行推力分配所致。通过对整个工作时间内积分可以得到系统总能耗变化情况,表2给出的功耗结果表明,40 s内加入分配器的能量最优分配与随机分配相比降至11.12%,可以从减小功率消耗的角度得到合适的分配结果。

4 结 论

针对空间站舱内微型服务机器人工作时位姿耦合控制的问题,本文设计了一种可以提供各方向均匀控制力的执行器布局模式,采用对偶四元数的建模方法给出了该布局模式下的舱内机器人六自由度耦合动力学模型,并基于该模型设计了控制器和力分配器,最终实现了收敛结果较好的稳定控制。同时,相比于随机的分配模式,加入本文所设计的力分配器后,可以从功率最优的角度得到最优分配结果。因此,本文所设计的考虑执行器最优分配的空间站舱内辅助机器人位姿耦合控制方法能够为后续更多的研究提供参考。