面向北斗异构星座的多参考一致性检验方法

贾 春，翁永琪，蒋家昌，李 亮，吉 斌，邹兆波

(1. 哈尔滨工程大学智能科学与工程学院，哈尔滨 150001；2. 中国船舶航海保障技术实验室，天津 300131)

0 引 言

卫星导航地基增强系统(GBAS)通过引入完好性监测算法,保障系统完好性与可用性,能够满足飞机着陆进近阶段的导航性能需求(RNP)[1-2],是基于性能导航的核心基础设施[3-5]。多参考一致性检验(MRCC)算法是GBAS完好性监测体系中的重要环节,直接影响着完好性监测性能。MRCC算法的基础原理是借助多个参考接收机冗余观测量构建检验统计量,通过监测多接收机观测量的一致性判别异常故障[6],在故障监测中被广泛应用[7-9]。RTCA-DO245A标准[10]中提供了一种基于极大似然估计准则的MRCC算法,通过利用多个参考接收机的差分校正量构建B值(B值表征为差分校正量一致性参数),对严重多径、接收机故障[11]等带来的测量异常值实施监测与排除,可以有效保障系统的完好性性能[12]。

MRCC算法通过构建监测阈值来保障播发差分校正信息的完好性[13]。如何综合考虑所需导航性能需求、卫星分布、星座类型、观测量质量等因素确定合理的监测阈值是至关重要的。目前,较为成熟的B值阈值构建方式大体有2种:美国联邦航空管理局(FAA)在FAA-E-2937标准[14]中根据飞机着陆进近阶段的完好性需求,考虑伪距差分信息的误差分布,提出了一种与卫星高度角和参考接收机数量相关的B值监测阈值构建算法,该方法故障监测灵敏度高、检测速度快。但该算法目前仅针对GPS卫星星座开展过模型拟合,并未针对北斗异构星座开展进一步研究,使得该模型不能适用于北斗卫星导航。Xie[15]通过分析大量GPS航空数据发现,实际卫星观测量呈现非高斯特性,需要采用高斯膨胀法对B值观测量实施高斯化处理,在此基础上,Zhang等[16]和胡杰等[17]基于北斗数据构建了B值监测阈值。然而,该方法是将全部空间与时间维度的卫星观测量整体实施高斯膨胀,忽略了不同高度角带来的观测量质量差异。此外,大量研究表明不同北斗异构星座MEO,IGSO,GEO的卫星观测量质量也存在一定差异性[18-21],因此也需要考虑不同卫星类型对于观测量质量的影响。

针对上述问题,本文提出一种面向北斗异构星座的多参考一致性检验方法,根据卫星观测量质量受到星座类型及高度角影响的特点,将检验统计量的样本空间网格化,实施高斯膨胀包络,得到适用于北斗异构星座的MRCC监测阈值,有效提高接收机异常观测量的监测灵敏度。

1 面向北斗异构星座的MRCC监测阈值改进算法

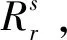
(1)

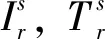
(2)

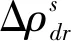
(3)

在澳大利亚科廷大学的公开网站http://saegnss2.curtin.edu/ldc/中下载2021年1月1日至2021年1月7日共7天的4台参考接收机数据,作为本文的试验测试数据。将北斗系统按照卫星高度角5°作为分区网格化,然后构建B值,得到不同高度角区间和不同卫星类型的B值标准差,如图1所示。由图可知,各类卫星的B值标准差随着高度角增大,整体呈下降趋势,这是因为随着卫星高度角增加,多径效应逐步降低,观测量质量有所改善;此外,由于不同卫星类型运行轨道限制,IGSO卫星在测试坐标点的高度角最高未超过85°,所以在图中拟合曲线上,缺少近90°的数值;而GEO卫星属于地球同步卫星,相对于测试坐标点的高度角基本无变化,所以在图中呈现出固定离散点现象,每个离散点表征着1颗GEO卫星。

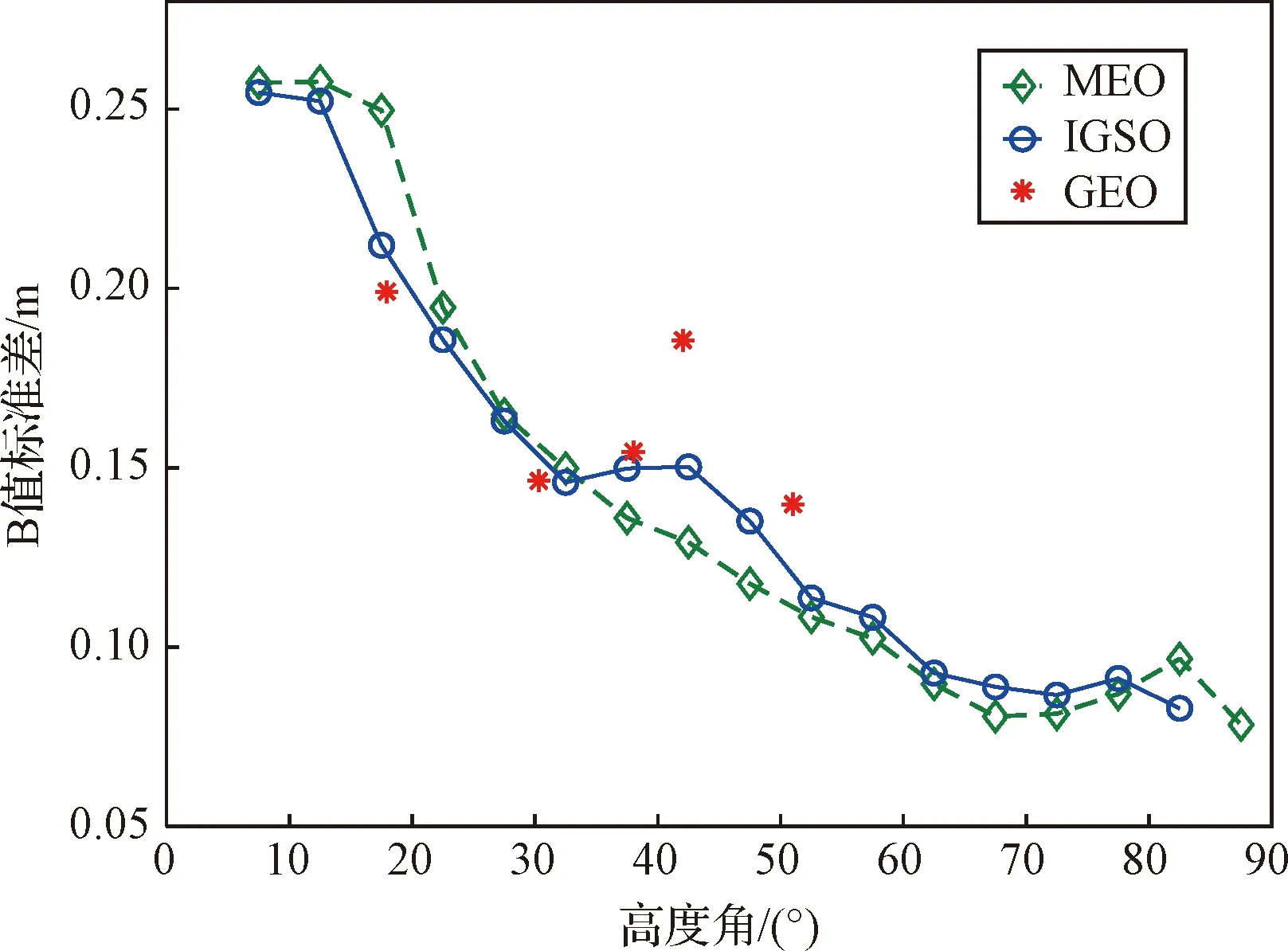
图1 B值标准差随高度角变化图

由图1可知,B值大小与卫星高度角及星座类型存在相关性,因此确定B值监测阈值应该充分考虑两者影响[16]。基于上述分析,本文提出根据不同卫星类型与高度角区间构建B值监测阈值,具体过程如图2所示。

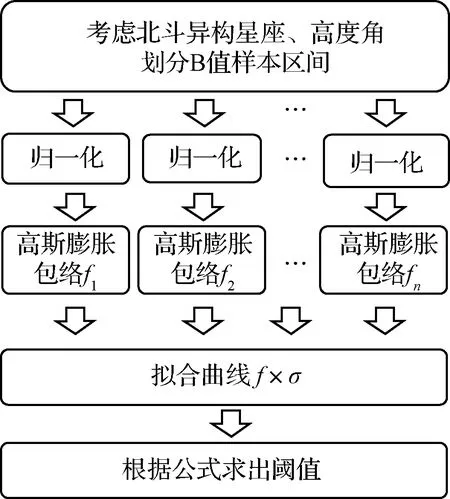
图2 改进阈值方法流程

首先,根据卫星类型及卫星高度角θ划分样本区间,分别计算MEO,IGSO及GEO三种不同卫星类型针对每个高度角区间的B值平均值μ和标准差σ;其次,根据平均值μ和标准差σ对每个区间B值进行归一化;然后,对每个区间B值实施高斯膨胀包络,得到该区间的膨胀系数f,并与对应区间的标准差σ相乘,使得各个高度角区间内的B值分布服从N(μ, (fσ)2),再得到所有卫星类型在[0°, 90°]区间内的拟合曲线;最后根据式(4)计算B值监测阈值T。

T(θ)=μ(θ)±Kffd×[fσ(θ)]

(4)

式中:Kffd是对应无故障完好性风险需求IH0,req的分位数,对应关系如图3所示,其计算过程为

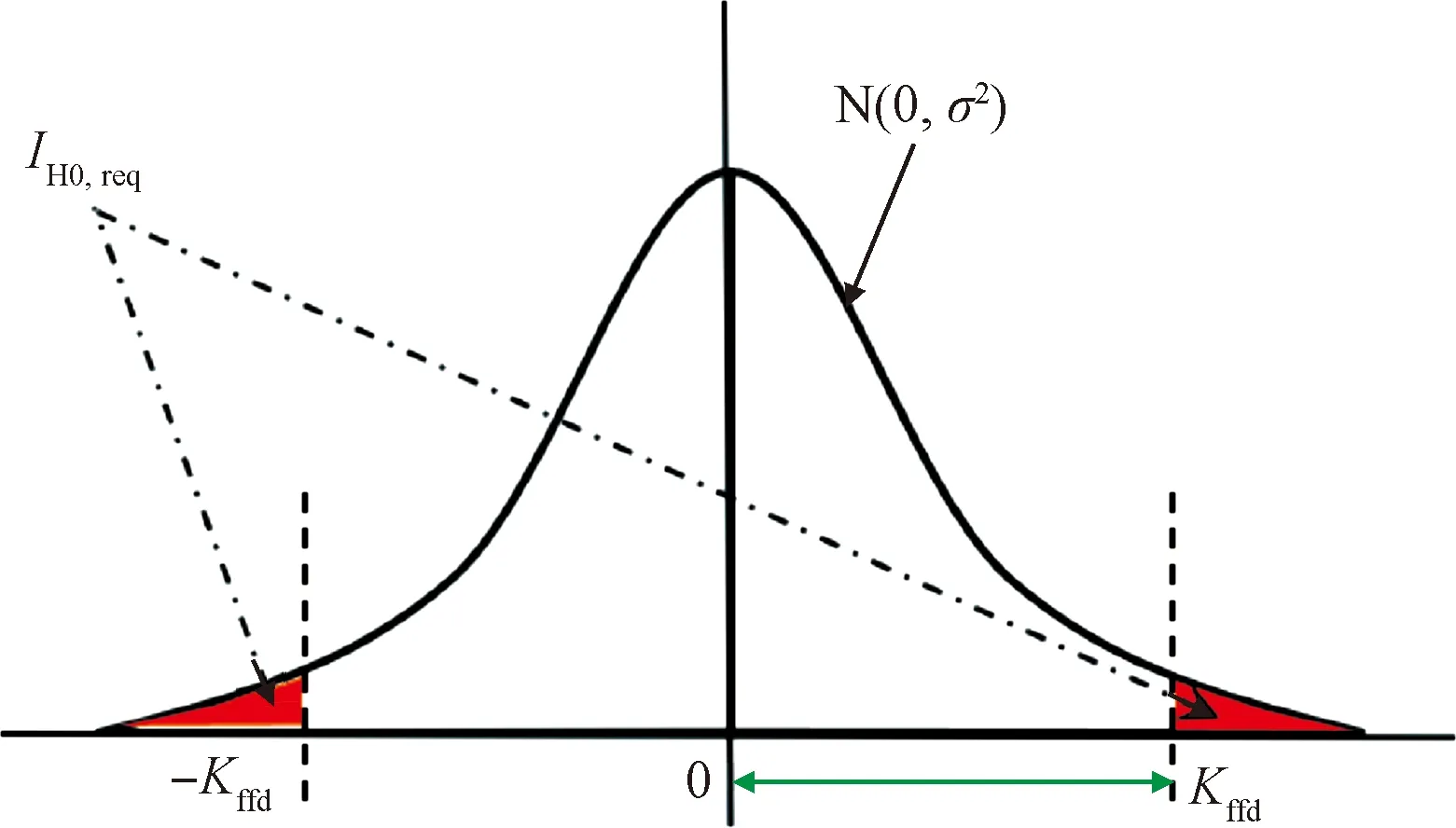
图3 分位数与无故障完好性风险需求的关系

(5)

其中,erfcinv(·)表示逆互补误差函数。国际民用航空组织(ICAO)规定了飞机I类精密进近与着陆导航的无故障完好性风险需求IH0,req应小于1×10-7[23],相应取Kffd=5.33。

改进方法按照不同卫星类型、高度角分区间实施高斯膨胀,细化了膨胀系数取值,优化了阈值计算方法,更加适用于北斗卫星导航的B值监测阈值构建。得到B值与监测阈值后,通过比较即可实现对异常多径、接收机故障的监测[17,24]。需要说明的是,实际GBAS一般配有4台参考接收机,如果因为接收机故障导致可用参考接收机低于3台,则无法支持着陆引导功能[3]。因此,观测量是否通过一致性检验,应该以B值未超限的参考接收机个数为标准。假设GBAS中有4台参考接收机,其MRCC的具体监测流程如图4所示。首先,确定多个参考接收机的可用公共卫星集,计算该集合内对应卫星B值,若无公共集合则告警;其次,由集合内卫星高度角计算得到监测阈值T。与B值进行比较,若存在B值大于T,找出最大B值,将构建该B值的参考接收机观测量标记为异常并排除,再根据剩余参考接收机的观测量重新计算B值。若此时无超限B值,表示仍有3台参考接收机的观测量可用,能够满足GBAS性能要求,通过一致性检验;若B值仍超限,此时观测量可用的参考接收机小于3台,无法满足GBAS正常工作需求,MRCC告警。

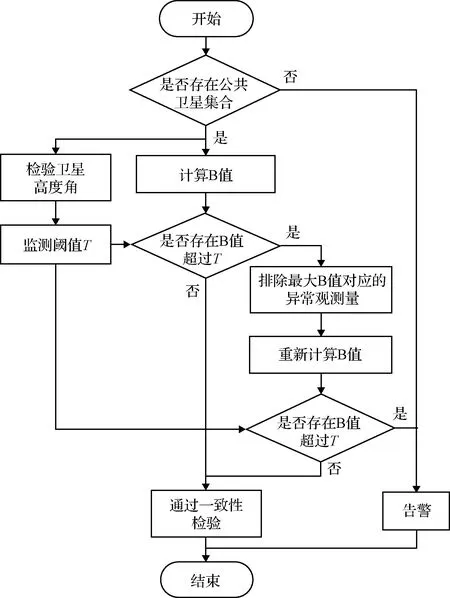
图4 MRCC监测流程

基于上述分析,分别使用传统方法和改进方法对阈值模型进行构建,其中传统方法不区分卫星类型和卫星高度角,将所有B值进行膨胀。通过包络所有B值样本点,得到传统方法的膨胀系数为f=2.550,结果如图5所示。

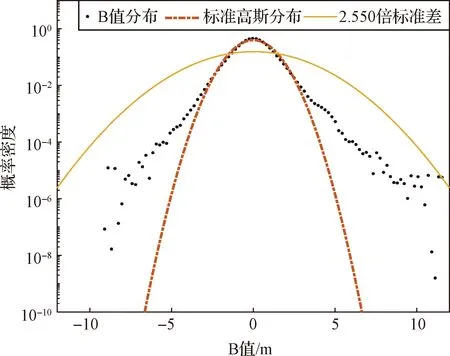
图5 传统高斯膨胀法的B值膨胀结果

改进方法则顾及不同高度角、不同卫星类型的情况,按照不同卫星类型及不同高度角区间进行膨胀,得到各B值标准差及膨胀系数见表1。

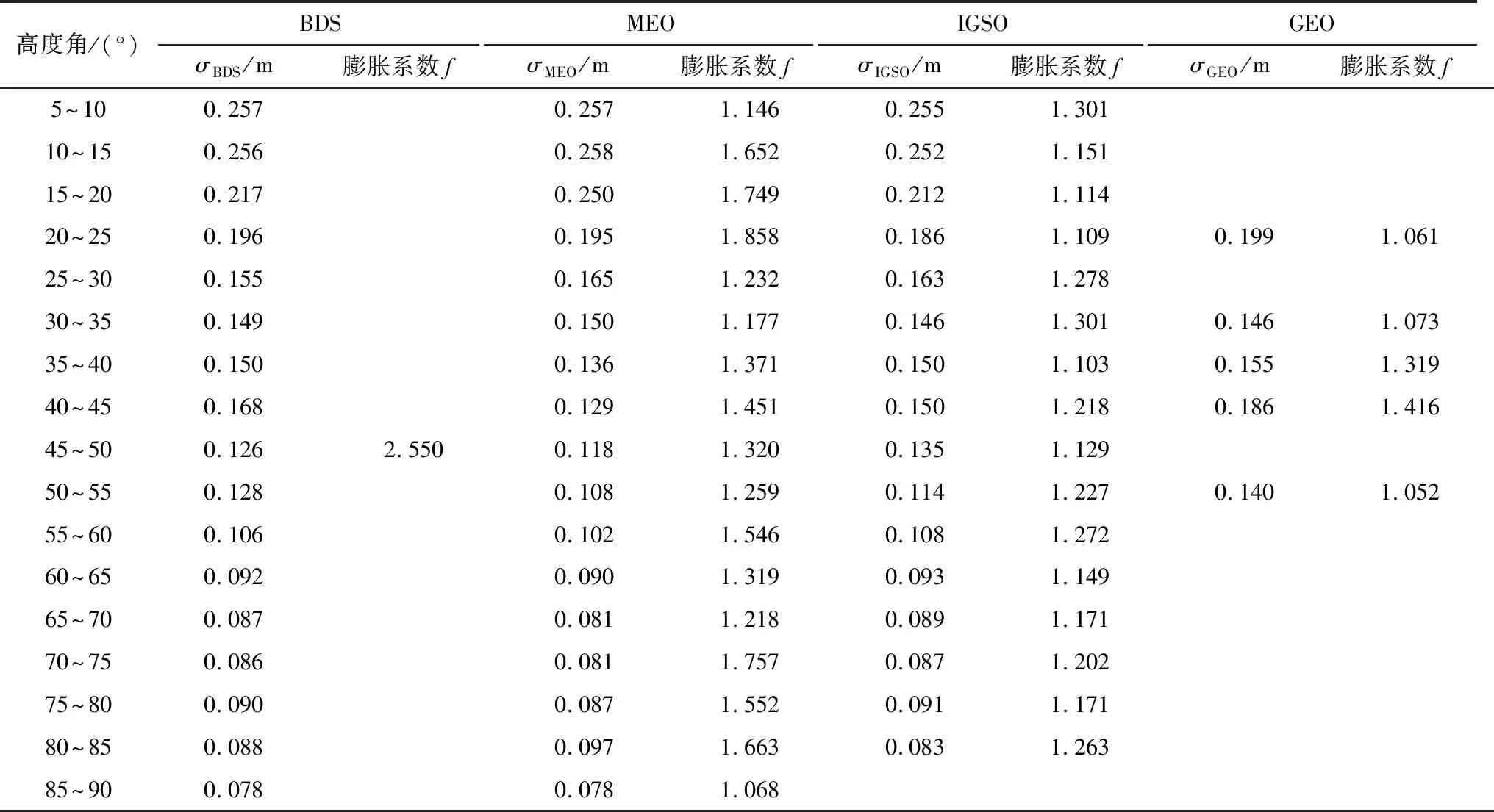
表1 北斗卫星的B值标准差及膨胀系数

根据表1和B值监测阈值构建式(4),通过指数拟合可得MEO,IGSO,GEO的阈值随高度角变化的模型如图6与表2所示。由图6可知,随着高度角增大,观测量质量更优,所有阈值曲线的变化也随之变小;由于改进阈值方法通过分区间膨胀,细化了各区间的膨胀系数,使其明显小于传统方法的膨胀系数。两类方法基于相同的无故障完好性风险需求构建阈值,理论上均能满足系统的无故障完好性风险需求。而传统方法较为保守,未考虑不同卫星高度角及卫星类型下B值统计分布的差异,对于全部观测量统一进行高斯膨胀化处理的方式导致监测阈值过大、监测结果过于保守,降低了故障的监测灵敏度。与传统方法相比,改进方法更为准确地刻画了B值的实际分布情况,在满足无故障完好性风险需求的同时,提升了故障监测灵敏度。

为推动食品安全城市创建工作，仓山区局牵头制定《食品安全城市创建工作方案》，列明全区各责任单位的10大项99小项工作要求，大胆探索社会共治，将创建工作纳入街道绩效考评的“街道共建”模式和在市场中引入业主责任制及第三方监管机制的“新西营里市场”模式，新西营里市场获评“全国诚信示范市场”。

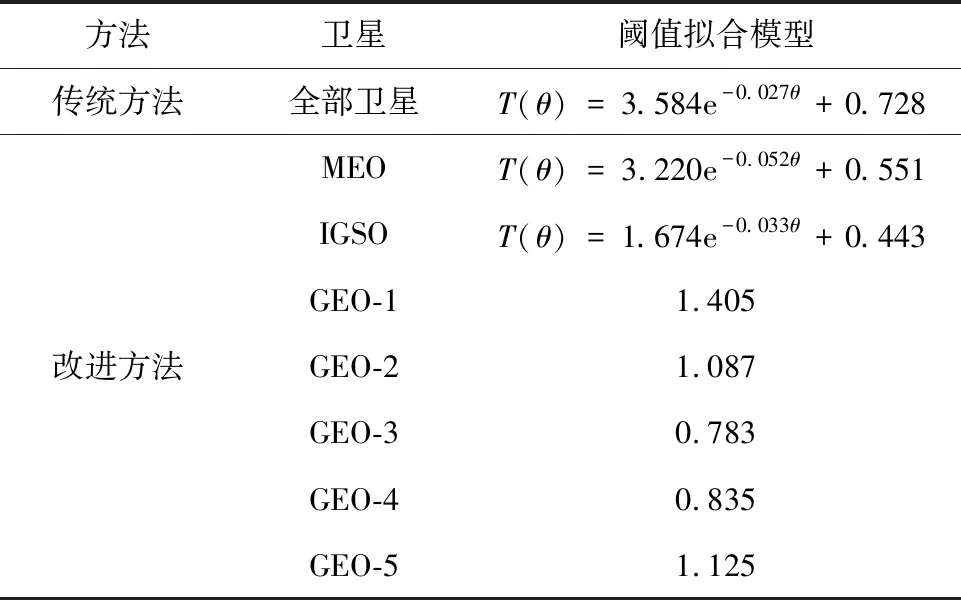
表2 B值监测阈值拟合模型

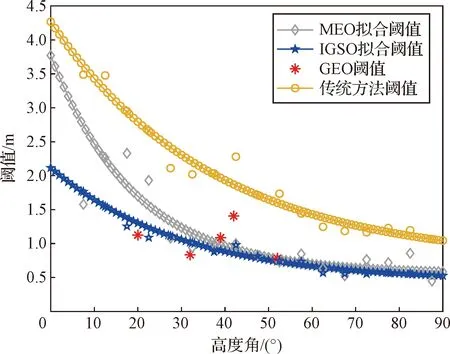
图6 B值监测阈值拟合模型

2 实验与结果分析

在澳大利亚科廷大学的公开网站http://saegnss2.curtin.edu/ldc/中采集一组多参考接收机数据,数据更新率为1 Hz,总时长为1小时,其中多参考接收机布设位置如图7所示,采样时段内北斗卫星可观测时长分布如图8所示。由于包含异常多径与接收机故障的实际数据难以获取,因此采用人为方式单独加入GBAS典型故障中常见的阶跃、缓变及加速度三类典型故障[16,25-26]对算法进行测试。为充分验证MRCC算法对故障的监测能力,在测试时段内,将CUTC接收机与卫星编号为1、2、3、4、5、7、8、10、13、27、28、30的12颗可见卫星的观测量通道中依次加入如图9所示的故障,模拟仿真接收机因故障产生的观测异常,从故障监测的灵敏度及对定位的改正效果两个方面对改进方法与传统方法进行对比分析。

图7 参考接收机布设位置

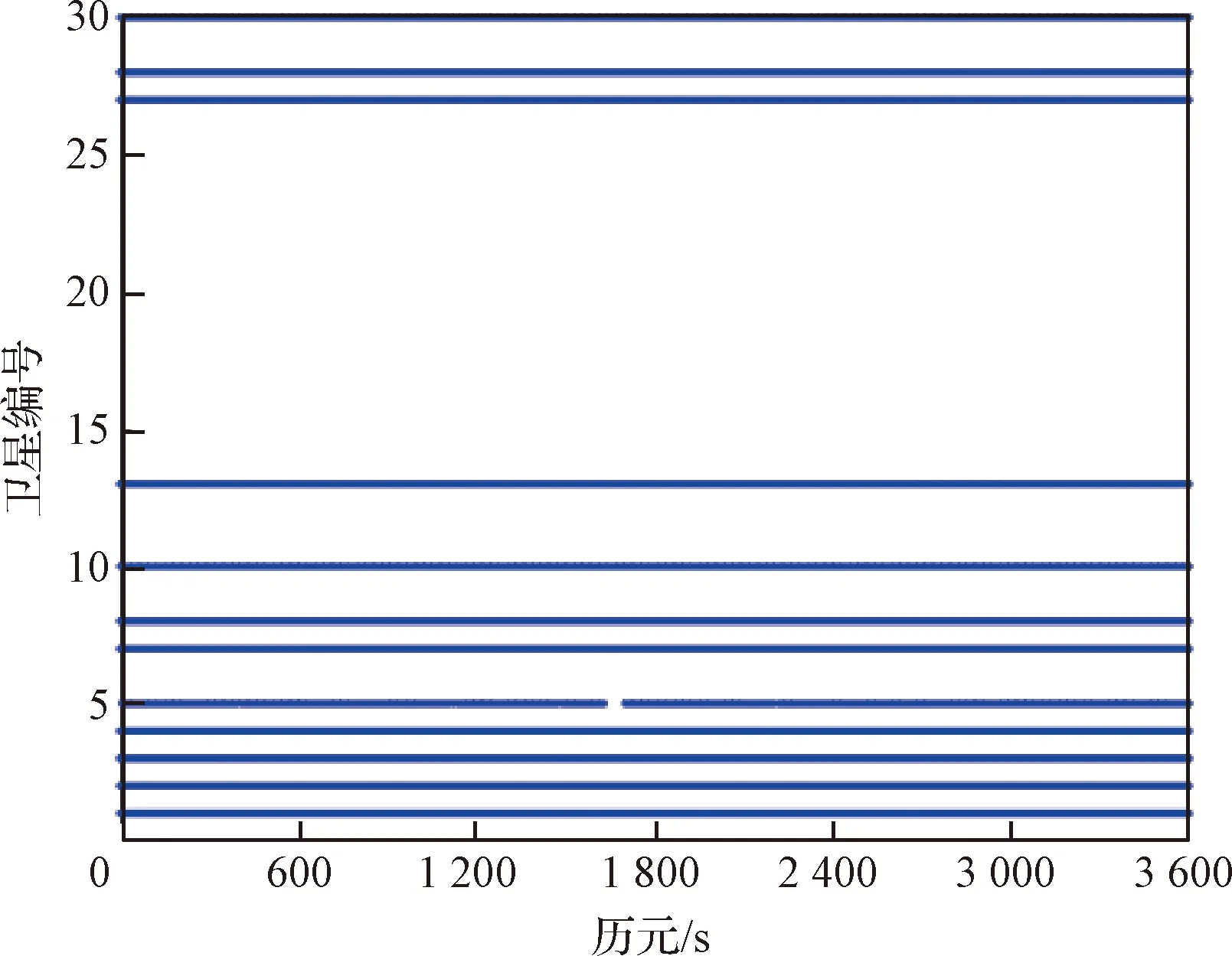
图8 北斗卫星可见卫星观测时长分布

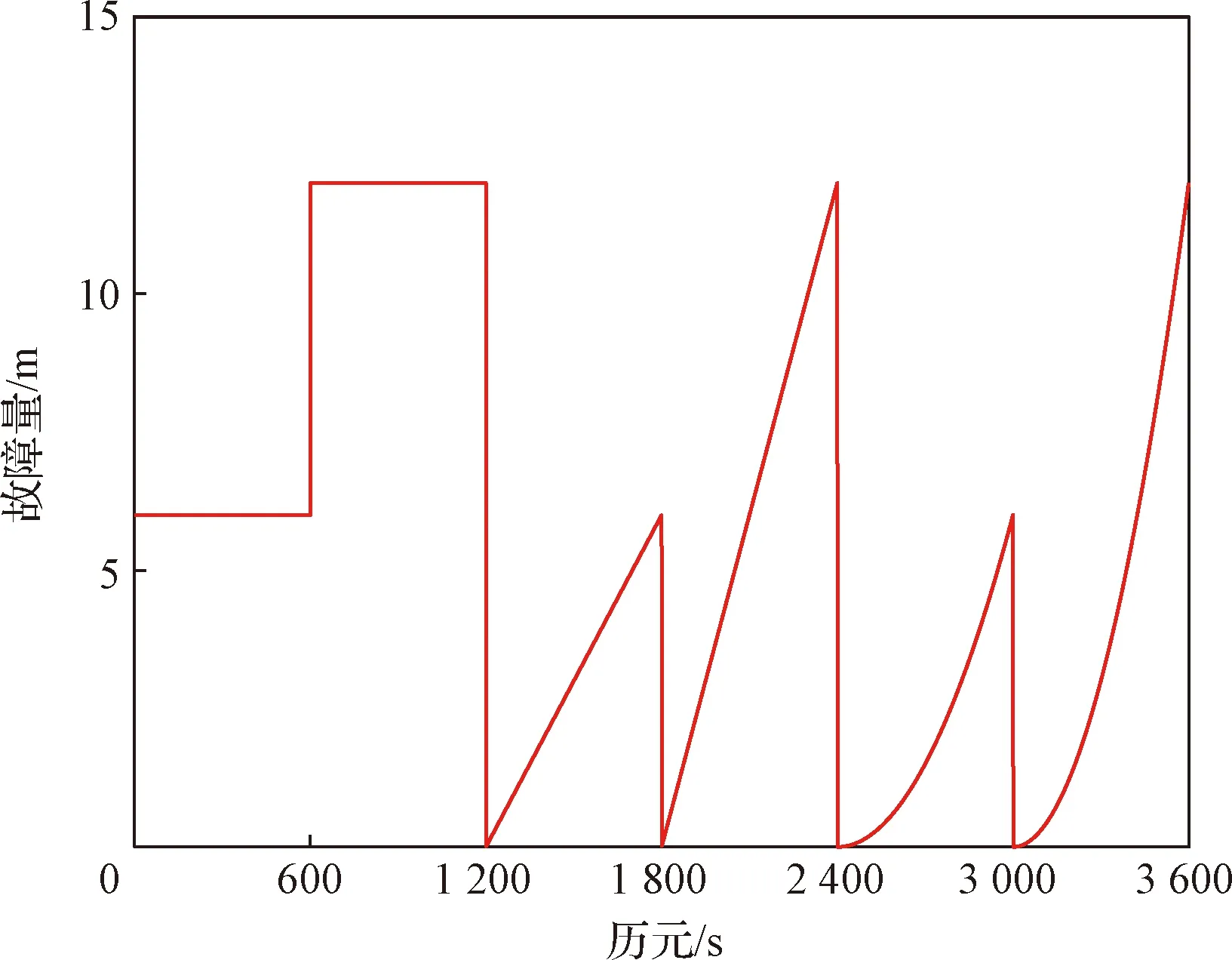
图9 人为加入故障类型、幅值与引入时间情况

需要说明的是,由于缓变型和加速度型故障具有故障施加连续性,能够量化灵敏度指标,因此本文将基于上述两类故障测试结果分析灵敏度指标。考虑论文篇幅,仅选择1号GEO卫星、8号IGSO卫星及27号MEO卫星作为典型卫星进行画图分析,结果如图10所示,其他可见卫星呈现相似结果,见表3。图10中的“IThres”表示改进阈值模型,“TThres”表示传统阈值模型,“未排除故障”指未使用任何手段对故障进行监测排除。

表3 故障监测情况及差分定位结果(SEP50定位指标)

根据图10中对三颗典型卫星观测量的MRCC监测情况可知,在观测量中加入故障时,对应的检验统计量B值会同步发生变化,如果B值超过阈值,MRCC算法会剔除存在故障的接收机,保障系统的完好性。观测量中存在第一段幅值为6 m的阶跃型故障时,传统方法难以发现CUTC接收机的故障,而改进方法更加精细化的阈值模型能够及时探测受故障影响的异常观测量,灵敏度更高。而在伪距观测量存在12 m的阶跃型故障时,B值同时超过传统方法及改进方法的阈值,两种方法均能完整实现对于异常观测量的探测。存在第一段缓变型故障时,随着故障的累积,传统方法较难发现存在故障的异常观测量,改进方法则在B值超出阈值时及时探测并排除了受故障影响较大的异常观测量。存在第二段缓变型故障时,两种方法均在一段时间后完成了对异常观测量的监测排除,而改进方法能够更加快速、灵敏地监测到故障。存在加速度型故障时,MRCC的监测过程与缓变型故障类似,传统方法难以探测第一段加速度型故障,对于第二段加速度型故障的探测也更为迟缓,改进方法能够探测第一段加速度型故障,对于第二段加速度型故障的探测也更为灵敏,由于加速度型故障前期变化缓慢,加速度型故障相比缓变型故障需要更长的时间实现对故障的监测排除。此外,由图10的定位误差可知,使用异常观测量进行导航定位会增大误差,改进方法能够更加快速、灵敏地探测到故障,排除异常观测量,有效提高定位精度。

其他可见卫星与典型卫星有类似的统计结果。由上述分析可知,在第二段缓变型、加速度型故障时,传统和改进方法能同时监测排除异常观测量,故针对缓变型、加速度型第二段故障的探测时间进行监测灵敏度比较分析;同时,为验证存在故障时改进方法对定位精度的改善效果,以SEP50作为定位指标统计不同监测方法下的差分定位结果,得到的监测情况与定位结果见表3。由表3可知,改进方法的灵敏度及定位精度相对于传统方法有了明显提升。进行一致性检验的卫星为GEO时,改进方法对于第二段缓变型故障的平均探测时间为199 s,对于第二段加速度型故障的平均探测时间为321 s,灵敏度较传统方法分别提升约为53.1%、34.4%,差分定位的平均精度为1.22 m,提升约为34.4%;一致性检验的卫星为IGSO时,改进方法对于第二段缓变型故障的平均探测时间为150 s,对于第二段加速度型故障的平均探测时间为292 s,灵敏度较传统方法分别提升约为53.6%、30.6%,差分定位的平均精度为1.16 m,提升约为13.4%;一致性检验的卫星为MEO时,改进方法对于第二段缓变型故障的平均探测时间为186 s,对于第二段加速度型故障的平均探测时间为358 s,灵敏度较传统方法分别提升约为52.1%、28.0%,差分定位的平均精度为1.16 m,提升约为20.1%。综合而言,改进方法相较传统方法能够提前监测到异常观测量并实施剔除,从而保障用户能够获得更好的定位性能。

3 结 论

本文提出了一种面向北斗异构星座的多参考一致性检验方法,可以有效提升多参考接收机对于异常观测量监测的灵敏度,保障GBAS发生故障时的导航性能与完好性。该方法综合考虑北斗不同卫星类型、不同卫星高度角的观测量质量差异,设计了一种改进的阈值监测模型。首先,将北斗系统的B值以5°高度角作为分区网格化,将卫星类型与高度角对于观测量质量的影响区分开;然后对于各网格区间的B值高斯膨胀包络,将各区间B值分布高斯化;再根据卫星类型指数拟合出MEO, IGSO, GEO的监测阈值。通过利用一组7天的多参考接收机数据对改进阈值模型仿真构建,仿真结果表明由观测量构建的检验统计量B值与卫星类型及卫星高度角相关,与分析一致;最后,通过人为加入阶跃、缓变、加速度等典型故障方式对改进方法的监测性能进行测试。测试结果表明,对于GEO, IGSO, MEO三类北斗卫星,相较于传统方法,改进方法能够探测幅值更小的阶跃型故障,对缓变型故障的灵敏度分别提升约53.1%、53.6%、52.1%,对加速度型故障灵敏度分别提升约34.4%、30.6%、28.0%。上述结果表明了所提方法能够提前探测受故障影响的异常观测量,有效消除因故障带来的定位误差,有利于保障用户的精度与完好性。