仅利用Crab脉冲星的径向/横向测距方法

刘 劲，贾运泽，王奕迪，马 辛

(1. 武汉科技大学信息科学与工程学院，武汉 430081；2. 国防科技大学空天科学学院，长沙 410003；3. 北京航空航天大学仪器科学与光电工程学院，北京 100191)

0 引 言

X射线脉冲星能为航天器提供径向上的速度与位置等信息,对深空探测自主导航具有重要意义。因而,X射线脉冲星导航备受国内外学者关注[1-4]。

自从1981年Chester等[5]提出X射线脉冲星导航的概念以来,美国就率先开展相关研究工作[6],并于2017年发射了中子星内部组成探测器[7-8],完成了X射线脉冲星导航空间验证。

从2006年开始,中国紧随其后,开展了X射线脉冲星导航研究工作,至今取得了一系列研究成果[9-11]。中国先后发射了天宫二号[12]、脉冲星导航实验卫星[13](XPAVN-1)、“慧眼”探测器[14],验证了脉冲星导航应用的可行性。

鉴于Crab脉冲星的流量远高于其他脉冲星,国内外X射线脉冲星导航实验的观测脉冲星都是Crab脉冲星(RSP B0531+21)。从Crab脉冲星累积轮廓中,不仅可以估计脉冲星到达时间,还可感知脉冲星累积轮廓的微弱畸变,以反演航天器在脉冲星径向上的速度信息。鉴于其他脉冲星流量极低,即使航天器搭载大面积X射线敏感器,仅能从接收的X射线脉冲星信号中估计出低精度的脉冲星到达时间,并且无法感知低流量的脉冲星累积轮廓的极微弱畸变。

1 脉冲星横向测距的科学机理

在非线性轨道中,由于位置误差传播,除径向误差外,横向位置误差也会引起径向位置误差,进而引起X射线脉冲星累积轮廓的畸变。本节将对此进行证明,并推导出位置误差与脉冲星轮廓畸变之间的关系,以此证明基于脉冲星畸变轮廓的横向测距方法的可行性。

图1给出了关于脉冲星径向与横面、轨道面、轨道投影、初始位置以及OTD的示意图。其中,轨道投影是指轨道在横面上的投影;位置角是以航天器飞行方向为正,当前位置相对于初始位置的转动角。如:初始位置角为0°;飞行1/2个轨道周期时,位置角为180°;飞行一个轨道周期时,位置角为360°。

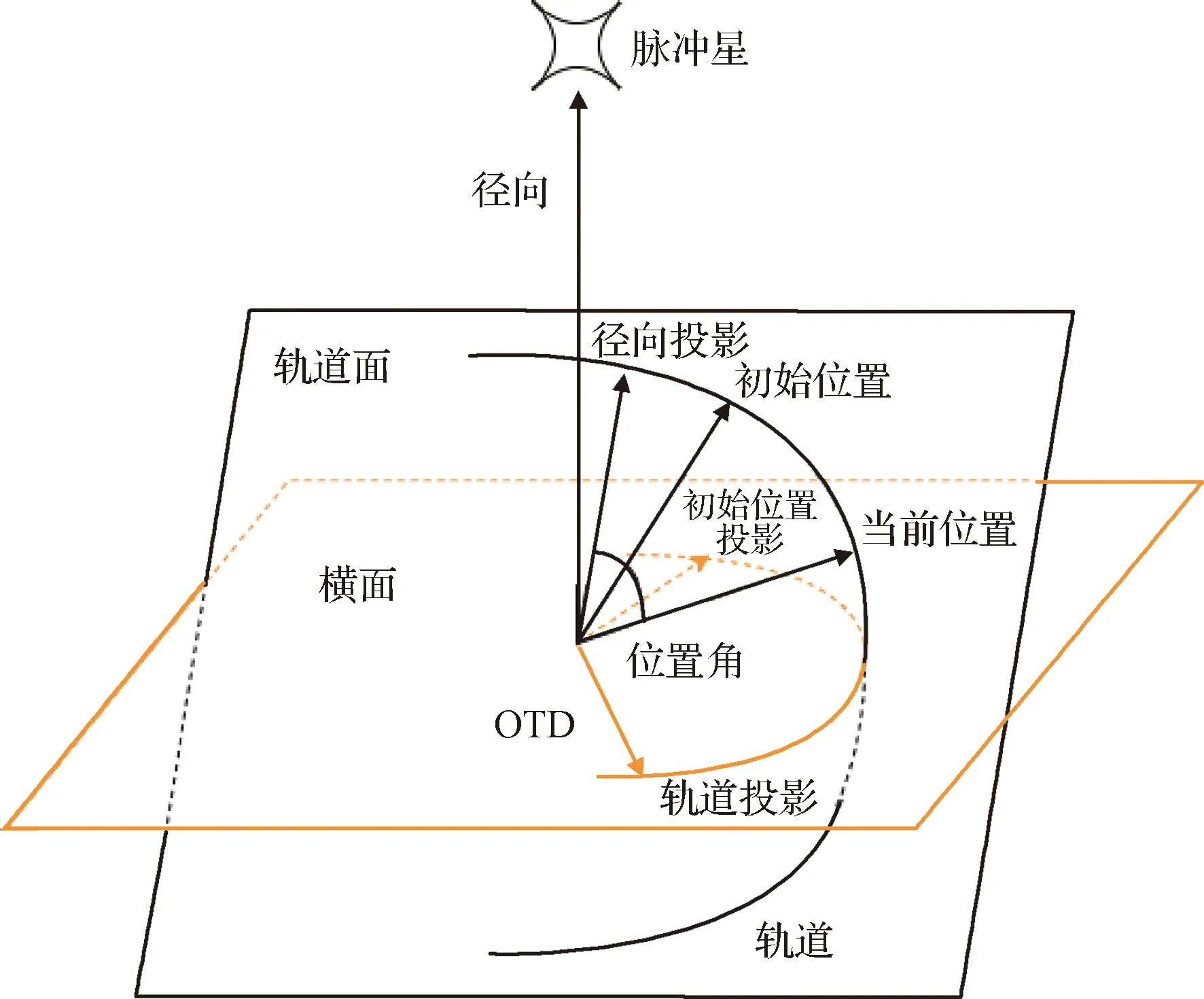
图1 OTD示意图

1.1 非线性轨道下径向上的位置误差

由于位置误差的传播性质,不同方向上的位置误差会互相影响,即在脉冲星横面上的位置误差必然会引起脉冲星径向上的位置误差,从而引起脉冲星轮廓畸变。下面,将证明这一性质。

位置误差传播性质1.在非线性轨道中,横向位置误差经传播导致径向位置误差。

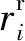
证.采用反证法。

在地心坐标系(J2000.0)下,轨道动力学模型如式(1):

(1)

式中:X为状态向量,w(t)为系统噪声。

将式(1)离散化可得到:

Xi=Φi,i-1Xi-1+Wi-1

(2)

式中:Φi,i-1≈Fi-1·ΔT+I6×6;I为单位矩阵;ΔT为采样周期;Fi-1为ti-1时刻的状态转移方程的雅可比矩阵,在忽略摄动项后,其表达式为:

(3)

令X0为航天器的初始状态向量,忽略噪声项和非线性量化误差,则有:

Xi=Φi,i-1·Φi-1,i-2…Φ1,0·X0

(4)

(5)

(6)

其在t1时刻的具体表达式为:

(7)

式中:δr0为t0时刻的初始位置误差。

同理,可得t2,t3,t4时刻的具体表达式,如式(8)～(10)所示。

(8)

(9)

S0S2ΔT4]·δr0

(10)

联立式(7)～(10),可得方程组。

若径向位置误差保持为零,即

(11)

脉冲星累积轮廓不会发生畸变。此时,唯一解为δr0=03×1。这就说明,若径向位置误差始终为0,初始位置误差必为0。反之,初始位置误差(包括初始横向位置误差)必会引起径向位置误差。

位置误差传播性质得证。

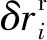
证.采用反证法。

式(8)减式(7),式(9)减式(8),式(10)减式(9),可得方程组(12):

(12)

若径向位置误差保持不变,即

(13)

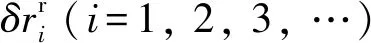
推论得证。

1.2 位置误差引起脉冲星轮廓畸变的形成机理

本节研究脉冲星轮廓畸变的形成机理。本质上,脉冲星累积轮廓可视为多个脉冲星子轮廓的叠加,具体如下:

为简化问题,忽略噪声干扰,仅考虑相移引起的脉冲星轮廓畸变。设归一化的脉冲星标准轮廓为h(φ)。其中,φ为脉冲相位;h(φ)的周期为1,即h(φ)=h(φ+1)。在脉冲星信号累积过程中,利用预估的径向位置对相移进行补偿。若存在径向位置误差,必然导致相位发生漂移。相移量Δφj为:

(14)

式中:T0为脉冲星固有周期;c为光速;Δφj为第j(j=0,1,2,…,J-1)个周期的径向位置误差引起的相位误差;J为脉冲星累积时间内的脉冲周期数。

(15)

根据1.1节中的位置误差传播性质及其推论,由式(15)可知,脉冲星累积轮廓是由不同相位的脉冲星子轮廓叠加而成,必然发生畸变。

若要使脉冲星累积轮廓不发生畸变,径向位置误差必须始终为零。根据1.1节的位置误差传播性质,径向位置误差若要始终为零,横向位置误差也必须为零;反之,横向位置误差必然引起径向位置误差。

以上脉冲星轮廓畸变的形成机理是通过脉冲星轮廓畸变反演横向位置误差的理论基础。这说明脉冲星横向测距是可行的。

2 径向/横向测距方法

本节研究径向/横向测距方法。相较于传统的X射线脉冲星导航方法,径向/横向测距方法引入了可观测横向方向这一概念。径向/横向测距方法并非能够估计脉冲星横面上任意方向的位置,而是在可观测横向方向上提供较高精度的位置估计。因此,该方法也被称为径向/OTD测距方法。

2.1 迭代循环互相关法

迭代循环互相关法是在循环互相关[22]的基础上,利用位置估计值修正初始位置值。循环互相关法适合于匀速直线飞行条件下的脉冲星TOA估计;而迭代循环互相关法适合于非线性轨道。这是因为在非线性轨道下,初始径向位置误差会引起径向位置误差增量。通过多次迭代,消除径向位置误差自干扰。迭代循环互相关法的流程图如图2所示。具体的算法流程如下:

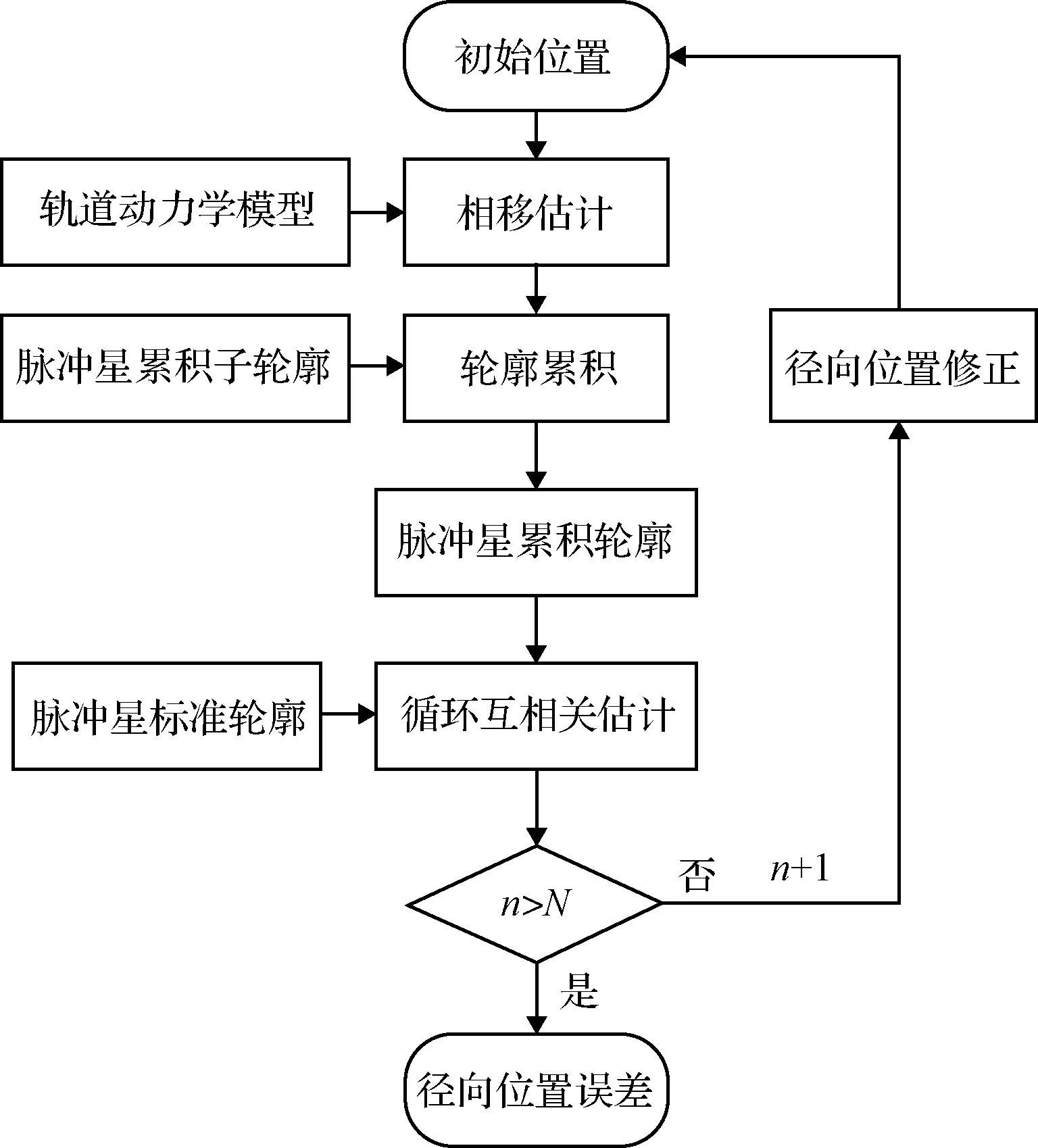
图2 迭代循环互相关法

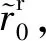
(16)

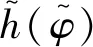
(17)

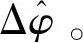
(18)

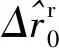
2.2 面向OTD2法

航天器的位置误差可以分解为三个相互垂直的分量。位置误差在脉冲星径向上的投影是径向位置误差;位置误差在脉冲星横面上的投影也可再次分解为两个垂直方向。根据第1节的位置误差传播性质与脉冲星轮廓畸变原理,脉冲星横面上的位置误差引起径向位置误差,进而导致脉冲星累积轮廓的畸变。经研究发现,横面内不同方向上误差引起的脉冲星轮廓畸变程度不同。引起的脉冲星轮廓畸变越大,该横向方向的可观测度越好。主要目的是在脉冲星横面内,确定引起脉冲星轮廓畸变最大的可观测横向方向。

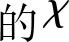
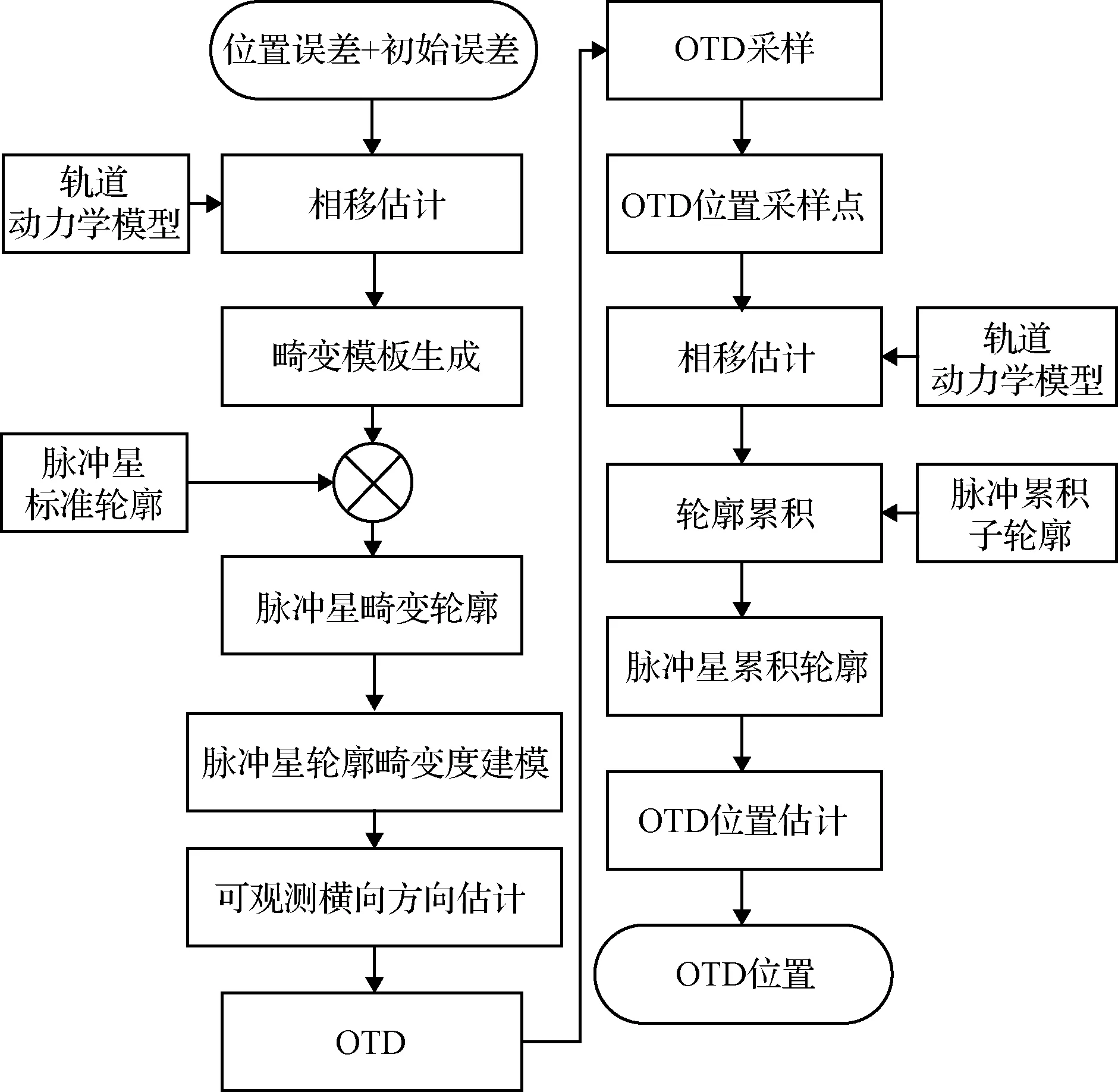
图3 面向OTD2法

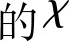
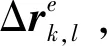
(19)

式中:δr表示采样间隔;N表示单个方向上的采样数;k和l为变量,k=1,2,…,N,l=1,2,…,N。这样可得N2个采样值。

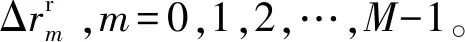
(20)

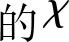
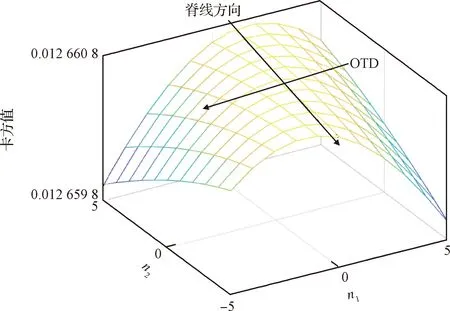
图4 脉冲星轮廓畸变度模型

径向/OTD测距法仅在山脊垂直方向估计,而非在山脊方向和山脊垂直方向同时开展二维估计。究其原因,一是在山脊方向估计,定位精度必然不高;二是脉冲星横面上的二维搜索必然导致计算量增大,影响X射线脉冲星导航系统的实时性。综上所述,本文仅在OTD上开展测距。

5) 可观测横向方向估计。构建脉冲星轮廓畸变度模型后,根据脊线方向可计算出可观测横向方向。通过函数拟合该山脊模型,拟合函数如下:

z=a0-b0|px-y+d|-e(py+x+c0)2

(21)

式中:a0为最大值;b0为当前值与最大值之间的斜率;p为脊线斜率;d和e分别为脊线的截距和曲率;c0为常数;x和y为n1和n2方向上的变量。通过拟合,即可估计出p。

可观测横向方向nOTD可通过下式计算:

nOTD=nr×(n1+p·n2)

(22)

式中:×表示矢量叉乘;n1+p·n2表示脊线方向矢量,其与脉冲星径向矢量nr的叉乘可得到脊线垂直方向矢量。

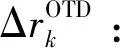
(23)

式中:δr表示采样间隔;N表示采样数;k为变量,k=1,2,…,N。

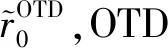
(24)

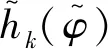
(25)

(26)

通过双一维搜索,分别求出了径向和OTD上的航天器位置矢量。与二维搜索相比,采样数大幅下降,计算量也必将大幅下降。通过先估计脉冲星径向位置,消除了径向位置误差的干扰,必然能有效提高OTD上的定位精度。

此外,通过后续3.2节的仿真实验可以看出,OTD与初始位置矢量有关。可根据初始位置快速确定OTD,从而避免了本节关于OTD的复杂计算,进一步减小了计算量。

利用三颗脉冲星的TOA进行解算,可得到航天器的三维位置。径向/OTD测距法可以通过一颗脉冲星的辐射信号估计出OTD和径向上的位置,再结合另一颗脉冲星的TOA实现三维定位。位置协方差矩阵C表示为

[(HTH)-1HT]T

(27)

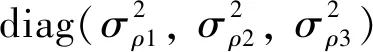
3 仿真实验与结果分析

本节考察仅利用Crab脉冲星的径向/OTD测距方法的准确性和实时性。下面将研究初始位置、累积时间、轨道半长轴、轨道倾角等因素对径向/横向测距方法的影响,并对比了双一维搜索法与二维搜索法。为了体现径向/OTD测距法的优越性,将采用三颗脉冲星的传统脉冲星测距法与采用两颗脉冲星的径向/OTD测距法作了对比。

3.1 仿真条件

导航脉冲星是Crab脉冲星PSR B0531+21,其基本参数如表1所示。研究发现,脉冲星累积时间与轨道周期均对OTD位置误差有影响。将脉冲星累积时间与轨道周期之比(RPATOP)作为径向/OTD测距法的重要参数。地心坐标系(J2000.0)下的地球卫星轨道六要素如表2所示。仿真实验平台是处理器为英特尔Core i5-8300H@2.30 GHz,内存为8G的联想笔记本。

表1 Crab脉冲星及X射线敏感器相关参数

表2 轨道六要素

3.2 初始位置与累积时间

为了探索脉冲星观测初始位置与估计精度之间的关系,本文用角表示轨道面位置,脉冲星径向矢量在轨道面上的投影为0°。图5给出了初始位置角及RPATOP对位置估计误差的影响。其中,图5中的初始位置角是指初始位置矢量与脉冲星径向矢量在轨道面上的投影之间的夹角。轨道周期约为5 215 s,RPATOP为1/2时,脉冲星累积时间约为2 607 s。

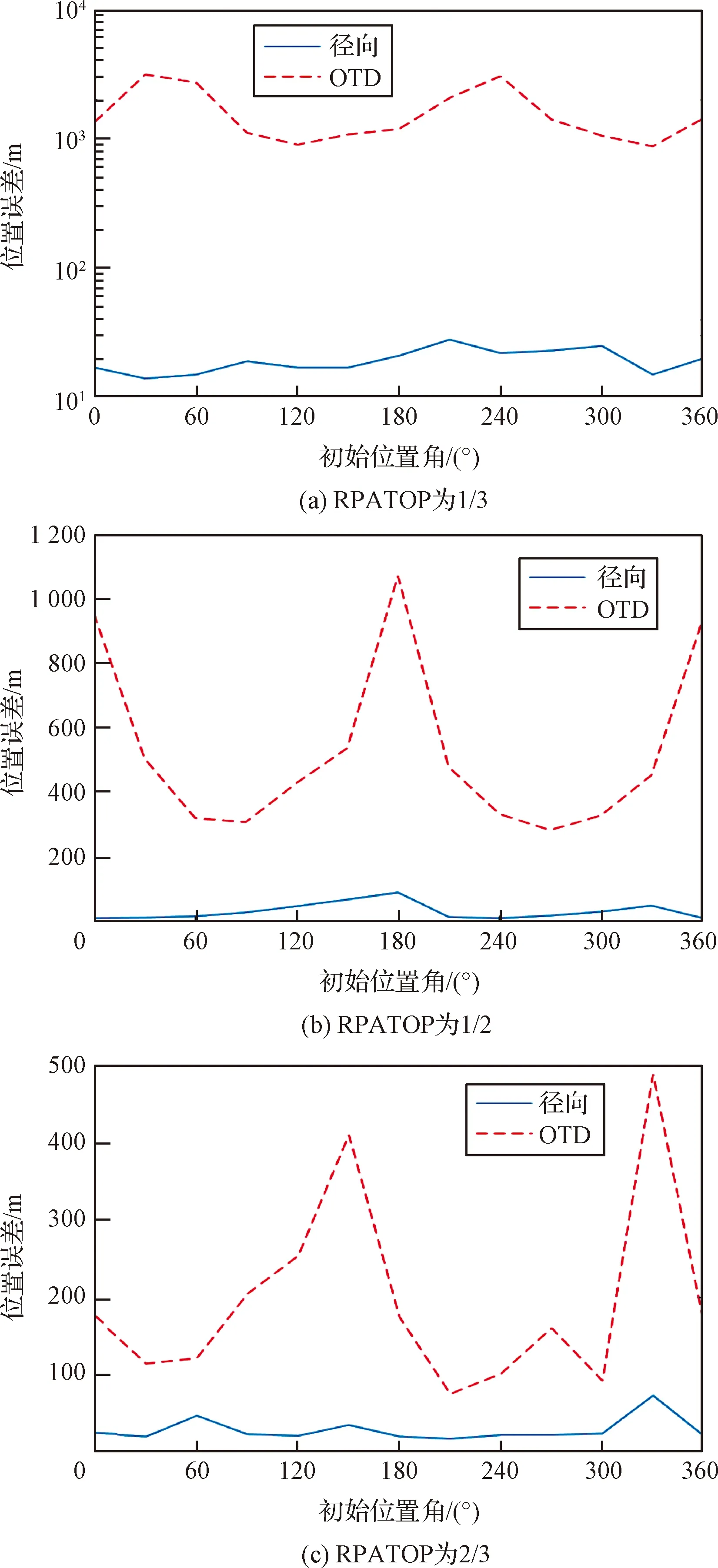
图5 初始位置角与RPATOP对位置估计误差的影响

从图5中可以看出,在不同RPATOP下,径向和OTD上的位置误差呈现两个波峰。这表明位置误差是呈周期变化的,且变化周期约为半个轨道周期。随着脉冲星累积时间的延长,径向和OTD上的位置误差均减小。通过以上现象可以得出,当RPATOP为1/2,且初始位置角为90°或270°时,径向/横向测距方法达到最优。原因有二:1) 精度高。此时的径向和OTD上的位置误差分别约为30 m和300 m,低于RPATOP为1/3时的位置误差。2)稳定。初始位置角为90°,累积完成后,下次的初始位置为270°,二者的精度相当。而RPATOP为2/3时,相邻的两次位置估计误差相差较大,不利于导航Kalman滤波器的设计。后续实验中,本文设置RPATOP为1/2。90°或270°时的初始位置定义为垂直初始位置。3.3节、3.4节、3.5节的仿真实验均是在垂直初始位置上开展的。

图6给出了RPATOP为1/2时,初始位置角与OTD角之间的关系。其中,OTD角是指OTD与初始位置矢量投影之间的夹角。从图6可以看出,OTD相对于初始位置矢量投影的位置角在小区间[-29°,-20°]内,且呈周期性变化。这一性质为OTD的快速确定提供了依据。导航系统在轨工作时,将初始位置矢量投影按照地面预先估算的结果,旋转特定度数即可得到OTD。在RPATOP为1/3和2/3时也符合类似规律,在此不再赘述。这样避免了2.2节OTD确定过程的复杂计算。

图6 初始位置角与OTD角之间的关系

此外,结合图5可知,即使OTD方位存在误差,其对应的位置精度并不会大幅下降。即使快速确定OTD时存在一定误差,也不会造成导航性能下降。因此,这是一种完全可行的方案。

3.3 半长轴

图7给出了轨道半长轴对径向和OTD位置估计误差的影响。从图7中可以看出,脉冲星累积时间随轨道半长轴延长,径向和OTD位置估计误差随轨道半长轴减小。

图7 半长轴对位置误差的影响

理论上,脉冲星位置估计误差应与累积时间的开方成反比。但是,OTD位置估计误差仅略微下降。究其原因,轨道半长轴越长,轨道非线性程度越弱。弱非线性轨道引起OTD上的位置估计误差增大。长累积时间和弱非线性轨道综合作用,使得OTD位置估计误差呈现图7所示的结果。

径向位置估计误差受非线性轨道的影响小,与累积时间的开方近似成反比。

3.4 X射线敏感器

X射线敏感器的性能与径向/OTD测距法息息相关。下面,考察X射线敏感器的时间分辨率和有效面积对径向/OTD测距法性能的影响,如表3所示。从表3可以看出,随着时间分辨率的下降和有效面积的减小,径向/OTD测距法的精度均下降。此外,时间分辨率的下降有助于缩短计算时间。究其原因,时间分辨率的下降意味着脉冲星信号数据的减少。时间分辨率的提高意味着需提升传感器工艺;而有效面积的增加则意味着载重的增加。在实际工程中,需综合考虑以上因素,选择合适的X射线敏感器指标参数。

表3 X射线敏感器性能

3.5 双一维搜索与二维搜索

表4 双一维搜索与二维搜索

3.6 传统脉冲星测距与径向/OTD测距法

若要实现三维定位,传统脉冲星测距方法需要至少三颗脉冲星(RSP B0531+21、B1821-24和B1937+21)。而径向/OTD测距法只需两颗脉冲星(RSP B0531+21、B1937+21)。传统脉冲星测距方法利用循环互相关法估计脉冲到达时间;径向/OTD测距法对RSP B0531+21在两个方向上估计位置信息,对B1937+21采用循环互相关法。估计完成后,直接利用式(27)求出协方差矩阵C。

根据C可得脉冲星三维定位误差,如表5所示。传统脉冲星测距方法需三颗脉冲星,径向/OTD测距法仅需两颗脉冲星;在不同X射线敏感器面积和时间分辨率下,径向/OTD测距法的定位精度均高于传统脉冲星测距方法。究其原因,弱脉冲星流量很低,导致测距精度低。其测距精度甚至低于Crab脉冲星OTD上的定位精度。

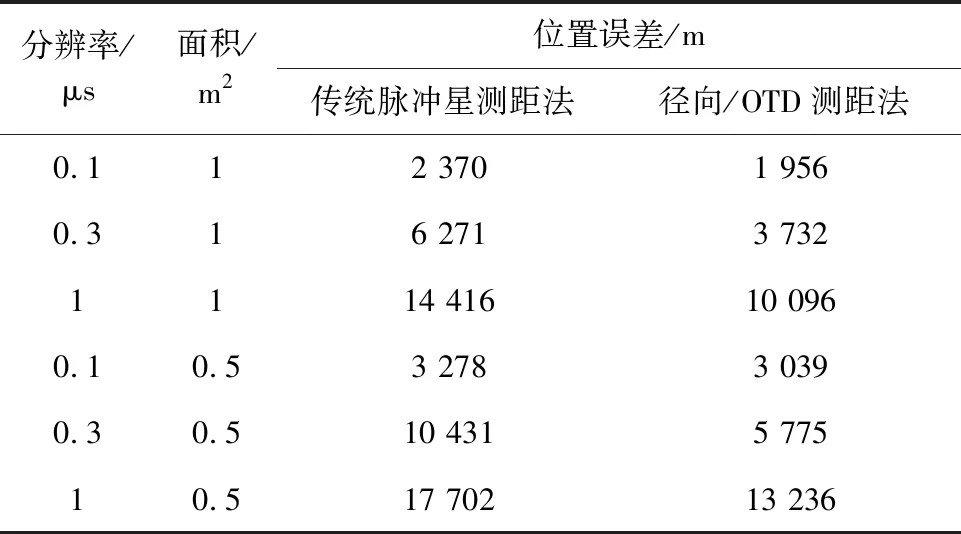
表5 两种脉冲星测距方法的比较

若采用传统脉冲星测距法,航天器需安装三个X射线敏感器分别对准三颗脉冲星,或者用一个X射线敏感器轮流观测三颗脉冲星。无论哪种方案都会增加导航系统的负担。径向/横向测距方法只需安装两个X射线敏感器分别对准两颗脉冲星,或者用一个X射线敏感器轮流观测两颗脉冲星。这无疑大大减小了导航系统的负担。综上所述,径向/OTD测距法优于传统脉冲星测距法。

4 结 论

传统脉冲星测距方法仅能在脉冲星径向上定位。针对这一问题,本文利用脉冲星累积轮廓畸变,开展OTD上的定位,并提出了仅使用Crab脉冲星的径向/横向测距方法。该方法分别使用循环互相关法和卡方法估计脉冲星径向和OTD上的位置信息。实验结果表明,径向/横向测距法仅利用Crab脉冲星就能在两个方向上实现定位,其径向和OTD上的定位精度分别约为30 m和300 m,计算时间仅需1分钟。与传统X射线脉冲星导航相比,基于径向/横向测距的脉冲星导航所需脉冲星数量少,且定位精度高。综上,该方法具有实时、高精度、强鲁棒等优点。若将径向/横向测距法应用于X射线脉冲星导航领域,可在降低系统负担的同时大幅提高定位精度,为未来X射线脉冲星导航系统设计提供新思路和理论参考。