基于Kriging代理模型的环形网状天线展开过程规划

杨癸庚，卫鑫鹏，2，樊 浩，汤奥斐，孔令飞，李鹏阳

(1. 西安理工大学机械与精密仪器工程学院，西安 710048；2. 中国电子科技集团公司第三十九研究所，西安 710065)

0 引 言

环形网状天线具备口径大、收纳率高、面密度小等优点,是目前大型可展开天线的理想结构形式,已被应用于电子侦察、空间通信、导航等领域[1-4]。由于受到航天运载工具限制,在卫星发射阶段,天线处于收拢状态并固定在火箭整流罩内,当卫星进入预定轨道后,天线展开至工作状态。环形网状天线的展开过程是一个受铰链摩擦、铰链间隙、索网张力、驱动索柔性等多种因素影响的非线性时变过程[5-6],天线能否在轨顺利展开决定着航天器任务的成败。因此,对环形网状天线的展开过程进行合理规划,是保证其正常工作的重要前提。

在环形网状天线展开过程规划方面,李团结等[7]提出了“匀加速-匀速-匀减速”的展开过程规划,该方法存在展开角加速度不连续问题,导致天线受到较大的冲击。Li[8]进一步提出了基于五次多项式的展开过程规划,该方法可以在一定程度上减小加速度冲击。为了进一步减小冲击,张逸群等[9-10]采用Bezier函数描述驱动绳索的收纳过程,通过优化设计驱动绳索的收纳过程实现天线展开角加速度峰值最小。然而,上述方法均基于运动学分析对天线进行展开过程规划,当考虑天线实际展开过程会受到铰链摩擦、索网张力、驱动索柔性等多种非线性因素的影响时,基于运动学的规划在天线的实际展开动力学响应中仍然可能存在较大的冲击[11-12]。因此,有必要进行基于动力学分析的天线展开过程规划。

高精度动力学分析模型是进行基于动力学分析的天线展开过程规划的前提。在环形网状天线动力学建模与分析方面,Li等[13]基于多体系统动力学的Lagrange方法,将内部索网张力等效为弹簧力,建立了环形网状天线的展开过程动力学模型,该方法将索网张力等效为线性弹簧力,导致建模精度不足。文献[14-15]从能量角度出发,分别针对圆环形和椭圆环形网状天线,推导了天线展开过程中索网弹性势能与展开角之间的非线性关系,该方法能够合理分析张紧索网对桁架铰链的作用力,但是难以描述展开初期索网的松弛状态。为此,Zhang等[16-17]采用弹性悬链线单元实现了索网结构松弛-张紧状态的统一描述,研究了展开过程中桁架铰链受到的索网张力变化规律,并通过实验验证了索网张力分析方法的正确性。此外,文献[11]建立了考虑铰链摩擦、索网张力及驱动绳索柔性的环形网状天线展开动力学模型,实现了综合考虑多种非线性因素的展开过程动力学分析。总之,随着动力学模型中考虑的因素越来越全面,建模精度越来越高,计算也会越来越耗时。若采用高精度动力学模型进行天线展开过程规划,虽然能够满足精度要求,但势必会导致总体优化过程因计算成本高而难以实现。因此,如何在保证计算精度的条件下提高优化效率是实现基于动力学分析的环形网状天线展开过程规划的关键。

代理模型技术是解决高精度分析模型计算耗时问题的有效途径[18-24]。目前常用的代理模型包括响应面模型[18]、径向基模型[19-20]、Kriging模型[21-24]等。各种代理模型中,Kriging模型适用于解决计算耗时大的黑箱问题,已在多个领域广泛应用。因此,本文将基于Kriging模型开展环形网状天线的展开过程动力学分析及展开过程规划研究。

本文基于Kriging模型建立环形网状天线展开过程动力学分析的代理模型,基于动力学代理模型提出非自适应和自适应两种优化策略对天线的展开过程进行最优规划,并通过案例分析研究不同优化策略的优化效果和计算效率。

1 环形网状天线展开过程规划问题

1.1 展开过程动力学模型

环形网状天线结构主要由环形桁架、索网结构和驱动绳索系统组成,索网结构在预张力的作用下张拉成形,环形桁架为索网结构提供边界支撑,如图1所示。

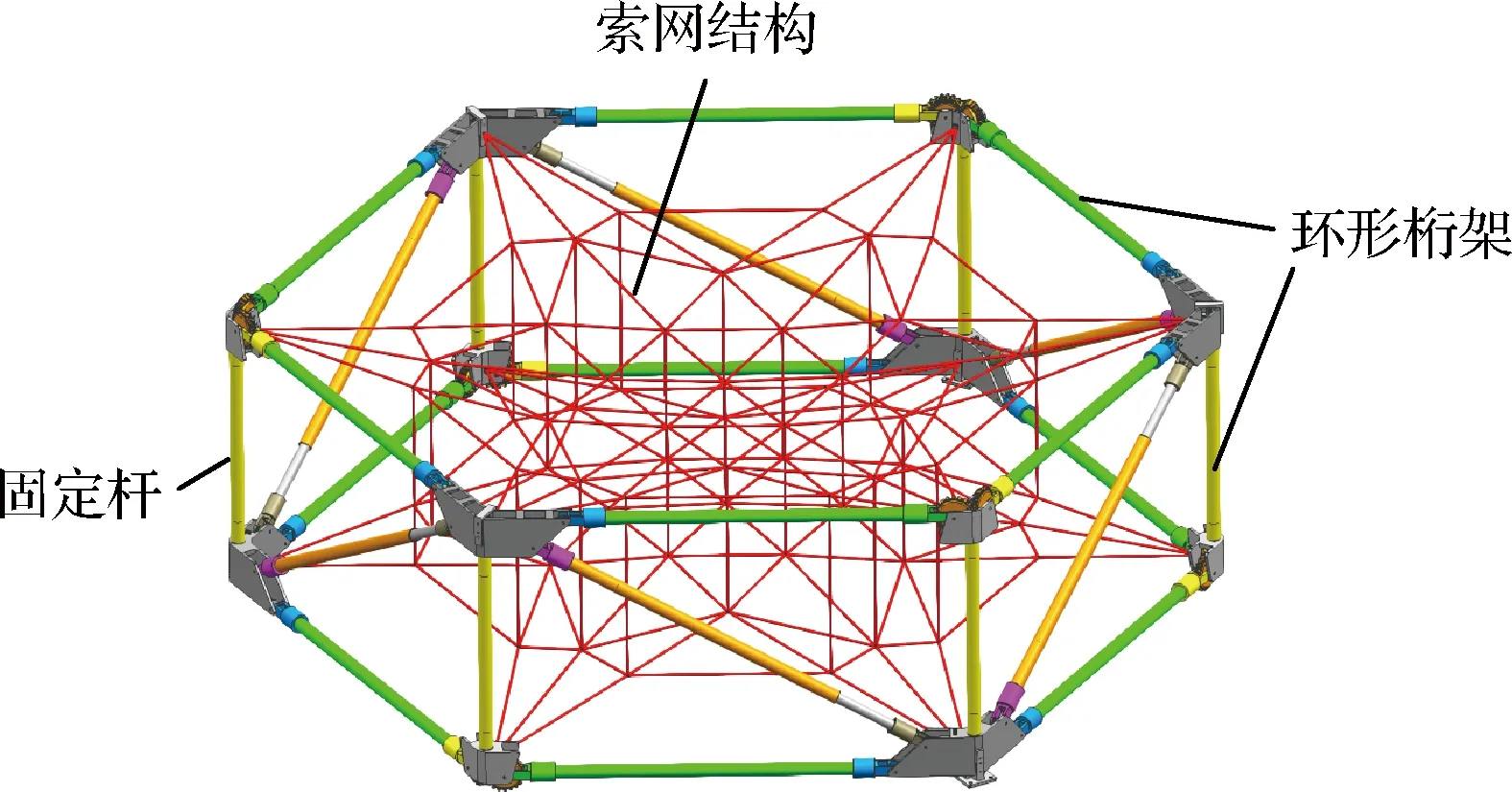
图1 环形网状天线整体模型

环形桁架由一系列基本的平行四边形单元组成,每个平行四边形单元由两个横杆、两个竖杆、1个粗斜杆和1个细斜杆组成,如图2所示。驱动绳索通过导向滑轮和空心斜杆贯穿于整个环形桁架中。驱动电机通过收纳驱动绳索改变四边形单元对角线长度,从而实现环形桁架的展开。

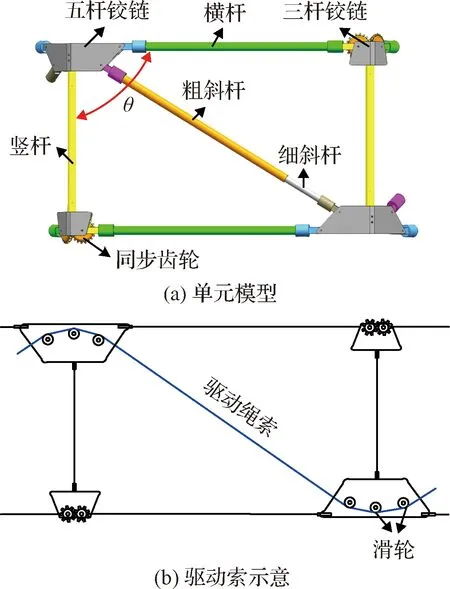
图2 平行四边形单元

天线展开过程中,环形桁架的杆件和铰链的弹性变形较小,可视为刚体单元[15]。与环形桁架相比,驱动绳索的柔性较大,将驱动绳索离散为多个小圆柱体单元,小圆柱体单元之间采用Bushing力连接,Bushing力的计算公式如下

(1)

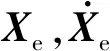
驱动索在运动过程中需要经过导向滑轮以确保在整个展开过程中驱动索与斜杆不发生干涉,驱动索与滑轮之间的相互作用采用接触力进行约束。展开过程中滑轮的弹性变形可以忽略不计,也视为刚体单元。

综上,基于拉格朗日乘子法建立同时考虑铰链摩擦、驱动绳索柔性和索网张力的天线系统展开过程动力学模型如下

(2)

式中:q为系统的广义坐标;M,C,K分别为系统的质量阵、阻尼阵和刚度阵;λ为拉格朗日乘子;Φ(q)为系统的约束条件;Φq为约束条件的雅克比矩阵;Q为系统受到的广义力。广义力Q可表示为

Q=Ff(t)+Fc(t)

(3)

式中:Ff(t)为系统受到的摩擦力,其大小由各个铰链处的摩擦系数决定;Fc(t)为张拉索网结构作用在桁架铰链上的时变外载荷,Fc(t)可通过文献[16]中的松弛索网找形方法确定。

1.2 展开过程规划问题

天线展开过程中,电机通过收纳驱动绳索改变平行四边形单元的对角线长度,从而驱动整个环形桁架实现展开。根据文献[10],驱动索长度的收纳过程可采用Bezier函数描述,通过合理设计Bezier函数的控制点参数可以获取天线的最优展开轨迹。

为减少天线在展开过程中受到的冲击力并降低驱动能耗、减少系统驱动成本,本文将展开角加速度峰值和驱动功率峰值最小化作为设计目标,建立基于动力学分析的天线展开过程规划优化模型(P-I)如下

(4)

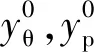
需指出,yθ(x)和yp(x)需要基于式(2)对环形网状天线进行展开过程动力学分析得到。由于环形网状天线的动力学模型中包含了铰链摩擦、索网张力、驱动索柔性等多种非线性因素,其动力学响应的求解过程耗时非常大,而优化模型(P-I)的寻优过程又需要对动力学模型进行多次调用,这将导致优化过程难以实现。为此,本文基于动力学代理模型对环形网状天线的展开过程进行最优规划。

2 基于Kriging代理模型的展开过程规划

2.1 Kriging代理模型

Kriging模型对于非线性程度较高的分析设计问题具有较好的拟合精度,可表示为[23]

(5)

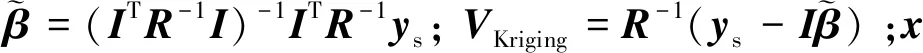
根据优化模型(P-I),环形网状天线的展开过程动力学分析的输入设计变量为描述驱动索收纳过程的Bezier函数的控制点参数x,输出目标函数为展开角加速度峰值yθ(x)和驱动功率峰值yp(x)。因此,基于Kriging模型构建环形网状天线展开过程动力学代理模型的流程如下:

1) 确定设计变量样本集。采用拉丁超立方试验设计方法[24]获得天线展开过程的控制点参数样本矩阵X。

2) 确定响应样本集。调用展开过程动力学模型,获取设计变量样本集X对应的展开角加速度峰值和驱动功率峰值的响应值,响应样本集可表示为

Y=[yθ,yp]

(6)

式中:yθ为展开角加速度峰值响应样本集;yp为驱动功率峰值响应样本集。

3) 确定样本集。用于构造Kriging代理模型的样本集为S=[X,Y]。

4) 构建代理模型。基于样本集S,根据式(5)构建环形网状天线展开过程动力学分析的代理模型,可表示为

(7)

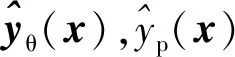
2.2 优化策略

根据样本点的获取方式不同,可将天线展开过程规划的优化策略分为非自适应策略和自适应策略两种类型。

2.2.1非自适应策略

基于非自适应策略的天线展开过程最优规划流程如图3所示。具体实现过程如下:

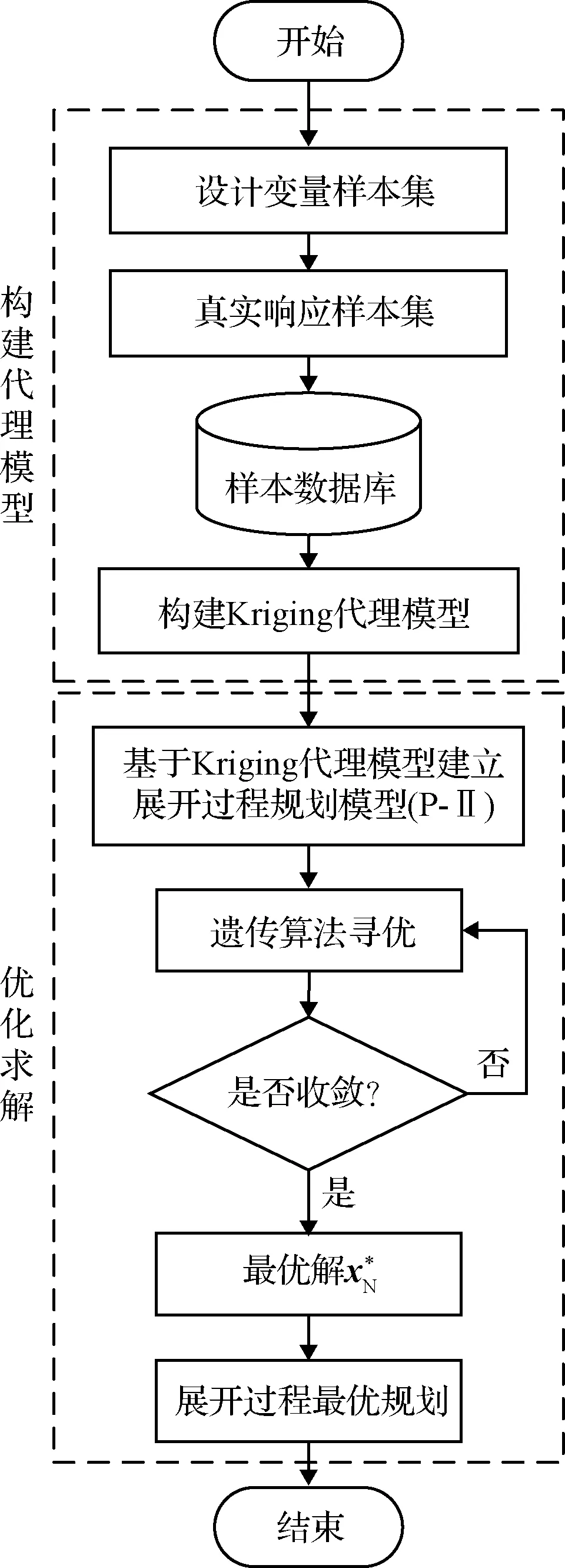
图3 基于非自适应策略的展开过程规划流程

1) 采用第2.1节的方法,基于Kriging模型构建环形网状天线展开过程动力学分析的代理模型。

2) 将优化模型(P-I)中的隐式目标函数更新为Kriging代理模型,则优化模型(P-I)可转化为模型(P-II)

(8)

3) 采用遗传算法对优化模型(P-II)进行全局寻优,直到满足收敛条件为止。

5) 输出天线展开过程最优规划结果。

基于非自适应策略的天线展开过程规划方法中,需要一次性采集足够多的初始采样点,才能保证Kriging代理模型的拟合精度,进而确保优化结果的有效性。

2.2.2自适应策略

为了在满足精度的条件下,减少样本点数目,进一步提高优化效率,提出基于序列采样方式的自适应优化策略。基于自适应策略的天线展开过程最优规划流程如图4所示。具体实现过程如下:

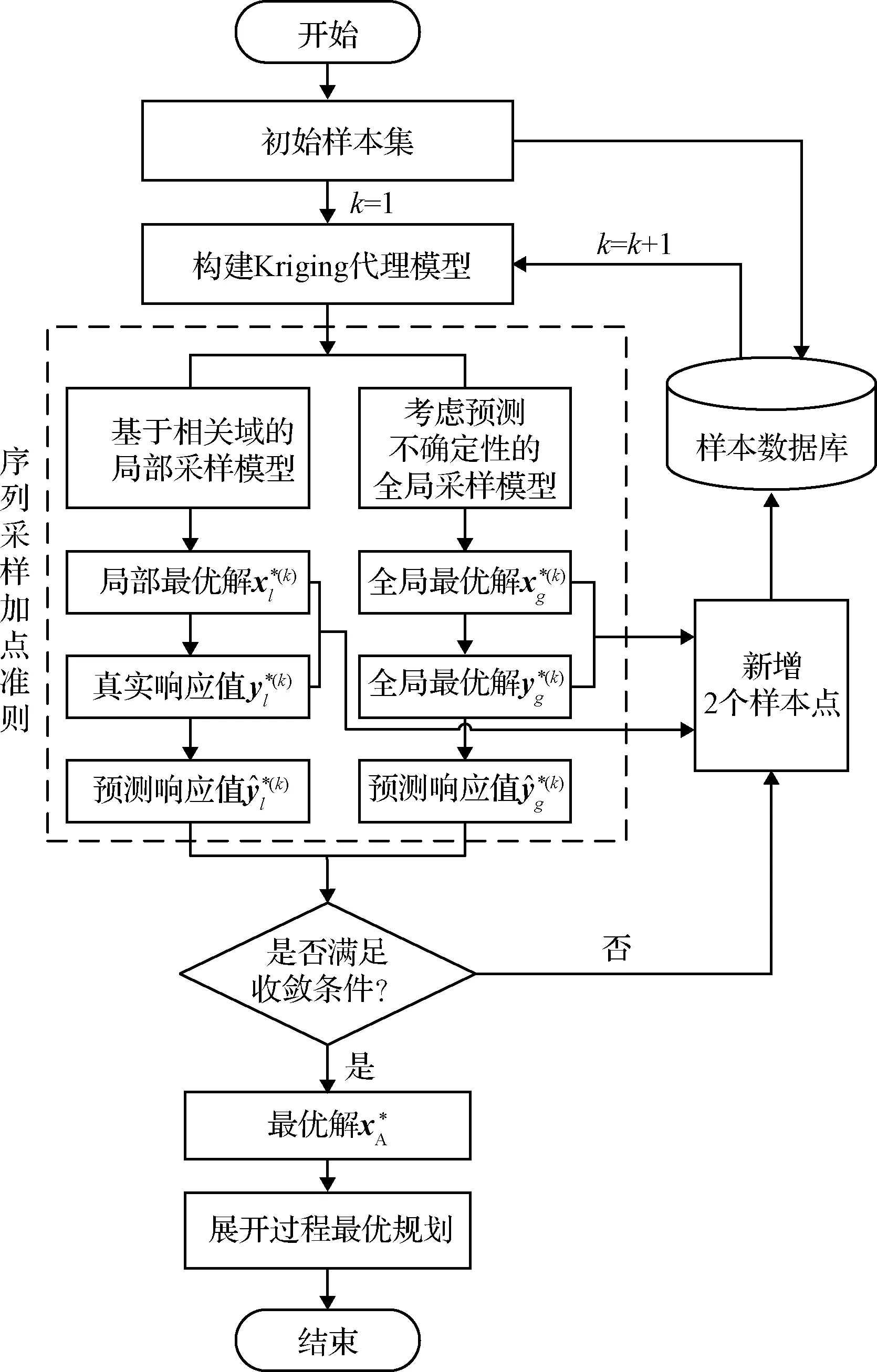
图4 基于自适应策略的展开过程规划流程

1) 确定初始样本集。采用拉丁超立方试验设计方法获取N0个初始样本点,并保存到样本数据库。初始样本点数量N0取为

(9)

2) 基于当前的样本数据库,采用第2.1节的方法,基于Kriging模型构建环形网状天线展开过程动力学分析的代理模型。

3) 构建序列采样的加点准则。采用平衡局部与全局寻优的方法,分别建立局部采样模型和全局采样模型,获取2个新增采样点。

(1) 对于第k个迭代步,建立基于相关域的局部采样模型(P-III)如下:

(10)

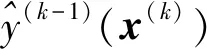
(11)

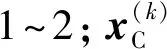
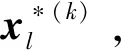
(12)

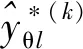
(2) 对于第k个迭代步,综合考虑Kriging模型的预测方差和设计点与已有样本点之间最小距离来构建全局采样模型,全局加点准则函数可表示为

|i=1,2,…,ns}

(13)

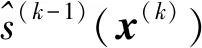
基于此,建立考虑预测不确定性的全局采样模型(P-IV)如下

(14)

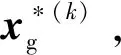
(15)

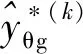
4) 判断当前迭代步的局部采样点是否满足收敛条件。若满足收敛条件,则执行步骤5);若不满足,则令k=k+1,并重复步骤2)～步骤4),直到满足收敛条件为止。为了保证目标函数迭代收敛且在最优解附近代理模型精度足够高,收敛条件为

(16)

式中:上标(k-1)和(k)分别表示第(k-1)次迭代和第k次迭代的结果,ε1,ε2,ε3,ε4为收敛精度。

6) 输出天线展开过程最优规划结果。

3 算例分析

3.1 模型参数

本文对图1所示的环形网状天线进行展开过程动力学建模与展开过程规划,该天线由6个平行四边形单元组成,天线展开态口径为1 m、高度为0.3 m、前后网面焦距为0.45 m。该天线模型中,杆件的材料为碳纤维,其弹性模量为150 GPa,密度为1.8×103kg/m3;铰链、同步齿轮和滑轮的材料为铝合金,其弹性模量为72 GPa,密度为2.7×103kg/m3;索网材料为芳纶纤维,其弹性模量为20 GPa,密度为1.685×103kg/m3;驱动绳索为钢丝绳,其弹性模量为150 GPa,密度为7.85×103kg/m3。

基于第1.1节的动力学模型,采用ADAMS软件建立环形网状天线的展开过程动力学仿真模型。仿真模型中,以图1所示的一个竖杆为固定端,设定各个铰链之间的摩擦系数为0.1,驱动索与滑轮之间的摩擦系数为0.01。

本例中,天线的展开周期为tp=10 s[25],选用10阶Bezier函数描述驱动索收纳长度的变化规律。根据角速度和角加速度的连续性条件[10],10阶Bezier函数所需要的控制点参数变量数目为5个。基于此,一旦给定一组控制点参数,即可通过调用动力学仿真模型得到天线展开过程的展开角加速度时程数据和驱动功率时程数据,进而可提取出整个展开过程中的展开角加速度峰值和驱动功率峰值。在电脑配置为CPU 3.70 GHz、内存16 G的条件下,单次调用动力学分析模型的计算耗时约为17 min。若直接采用优化模型(P-I)进行环形网状天线展开规划,寻优过程需要大量的搜索才能找到全局最优解,往往需要成千上万次调用动力学分析模型,总体优化过程的计算成本会非常高甚至难以实现[20]。因此,有必要采用基于代理模型的优化策略进行环形网状天线的展开过程规划。

3.2 基于非自适应策略的展开过程规划

采用第2.2.1节的非自适应策略对天线的展开过程进行最优规划。

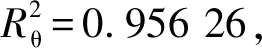
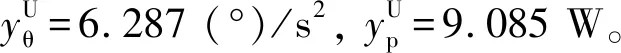
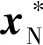
非自适应策略的优化结果如表1所示,与文献[10]相比,本文方法得到的天线展开角加速度峰值及驱动功率峰值分别下降了1.64%和18.41%。因此,与运动学规划相比,基于动力学分析的天线展开过程最优规划可以进一步减小展开角加速度峰值和驱动功率峰值。

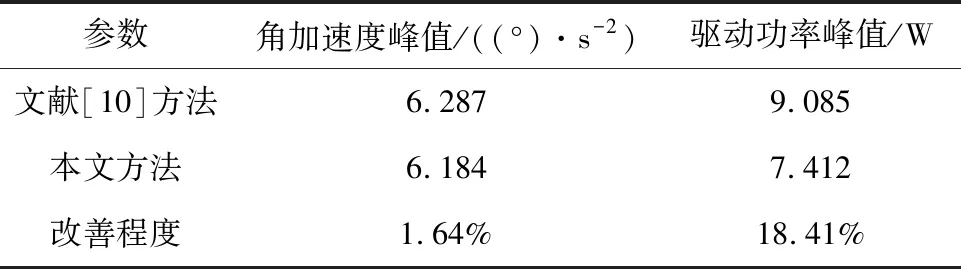
表1 非自适应策略的优化结果

3.3 基于自适应策略的展开过程规划

为了在满足精度的条件下,进一步提高优化效率,采用第2.2.2节的自适应策略对天线的展开过程进行最优规划。

根据式(9),初始样本点数目取为N0=21。同样将基于运动学规划方法[10]得到的控制点参数x0作为设计变量初始值。取收敛精度εi=0.001(i=1～4)整个优化过程经过11次迭代达到收敛条件,目标函数的迭代曲线如图5所示。可知,整个优化过程中,对动力学仿真模型的调用总次数仅有43次。

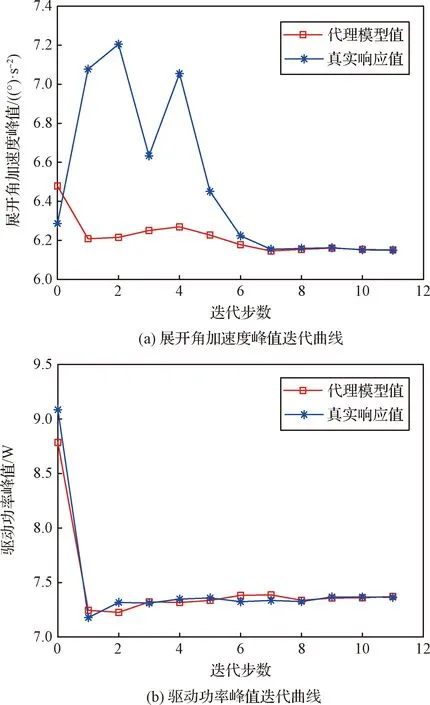
图5 自适应策略的目标函数迭代曲线

自适应策略的优化结果如表2所示,与文献[10]相比,本文方法得到的天线展开角加速度峰值及驱动功率峰值分别下降了2.18%和18.93%。

表2 自适应策略的优化结果

3.4 结果对比

非自适应策略和自适应策略的优化结果及计算效率对比情况如表3所示。可知,在目标函数改善方面,两种优化策略得到的结果很接近,自适应策略得到的展开角加速度峰值仅降低了0.55%,驱动功率峰值仅降低了0.63%。在计算效率方面,自适应策略对动力学仿真模型的调用次数从非自适应策略的160次减少到了43次,计算效率提高了73.12%。

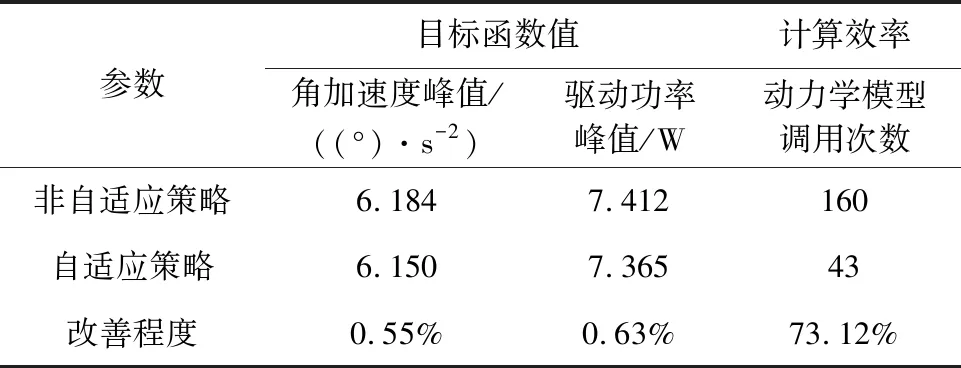
表3 不同优化策略结果对比

(17)

式中:tp为天线的展开周期,本例中tp=10 s。

将式(17)中的驱动索收纳长度最优规划作为输入,对天线进行展开过程动力学分析,可得到天线展开过程的最优响应。优化后的天线展开角响应情况如图6所示,驱动功率变化情况如图7所示。

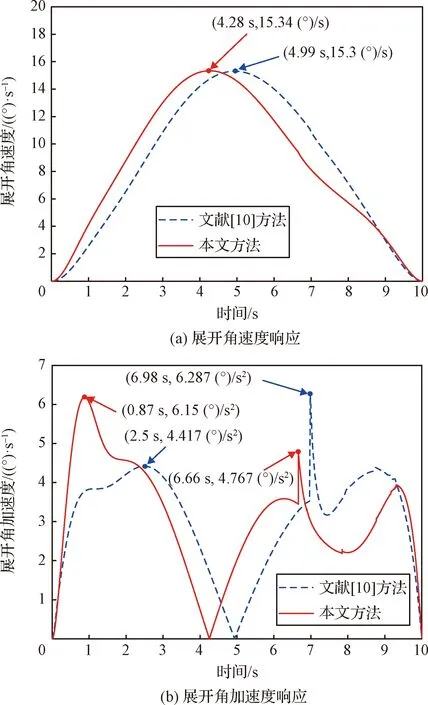
图6 优化后的天线展开角响应情况

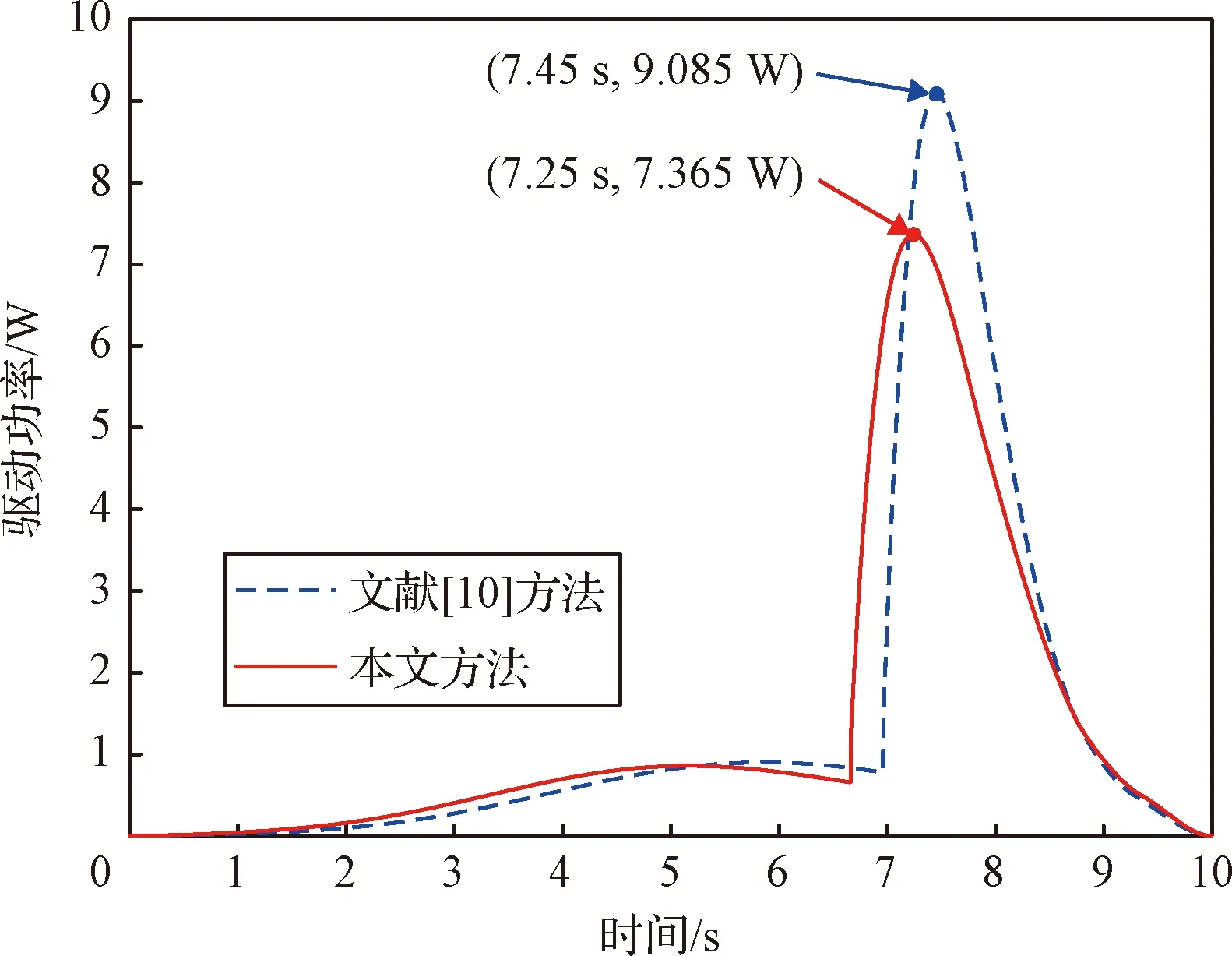
图7 优化后的驱动功率变化情况

由图6(a)可知,优化后天线展开角呈现先加速、后减速的运动规律,减速阶段的起始时刻由优化前的4.99 s提前至4.28 s。由图6(b)可知,加速展开阶段的展开角加速度峰值比优化前增大,减速阶段的角加速度峰值比优化前减小,整个过程的角加速度峰值由6.287 (°)/s2降低至6.150 (°)/s2。

由图7可知,优化后驱动功率的变化过程均可分为两个阶段:1)索网结构松弛阶段,该阶段驱动绳索需要克服运动副的摩擦阻力,驱动功率随着展开过程的先加速、后减速运动规律也呈现出先逐渐增大再减小的趋势;2)索网结构逐渐张紧到天线完全展开阶段,该阶段驱动绳索需要克服摩擦阻力和索网张力的共同作用,由于该阶段索网对桁架的作用力呈现先增大再减小规律[16],天线的展开速度则逐渐减小直到速度为零时完全展开,所以该阶段驱动功率也呈现先增大再减小为零的趋势。整个展开过程中,驱动功率的峰值从优化前的9.085 W降低至7.365 W。

4 结 论

本文提出了一种基于动力学分析的环形网状天线展开过程规划方法。基于Kriging模型构建了环形网状天线展开过程动力学分析的代理模型,并提出了展开过程规划的非自适应和自适应两种优化策略。研究结果表明:

1) 通过构建环形网状天线展开过程动力学分析的代理模型,有效解决了高精度动力学模型在展开过程规划中带来的高计算成本问题,实现了基于动力学分析的展开过程规划。

2) 在传统运动学规划方法的基础上,基于动力学分析的环形网状天线展开过程规划方法可以进一步降低天线的展开角加速度峰值和驱动功率峰值。

3)通过对比非自适应和自适应两种优化策略可知,自适应策略减少了高精度动力学模型的调用次数,能够在保证最优解附近代理模型精度的条件下大幅度提高优化效率。

综上所述,基于动力学分析的环形网状天线展开过程规划方法可为环形网状天线实现小冲击、低能耗展开提供一定的实际指导作用。