固体弹道导弹大气层外弹道飞行时间控制方法
桂 航,孙瑞胜,刘宣廷
(南京理工大学能源与动力工程学院,南京 210094)
0 引 言
随着世界主要军事强国的反导拦截技术快速进步,反导武器的射程、速度以及机动能力等都大幅提高,各类间谍卫星、预警机、陆基和海基探测雷达构筑起海、陆、空、天多维度的侦察探测体系,对弹道导弹从远中近界、高中低层进行全方位的电子对抗与硬杀伤拦截,这些侦察拦截手段对弹道导弹实现突防打击带来巨大挑战。在这种背景下,弹道导弹的生存能力在战场对抗中显得尤为重要,突防能力已逐步成为衡量弹道导弹性能的核心指标。多弹协同突防被认为是提高导弹突防能力的有效手段,通过信息化和智能化手段使导弹拥有信息共享、任务分配、任务改变等能力以提高突防成功率,同时还兼顾了毁伤能力的提升。
导弹协同作战是指由相同或者不同类型的多枚导弹组成编队,在任务规划系统的导引下,根据各方面要求进行时间、空间以及信息共享等方面的协同,以提高突防打击能力,完成战略或战术打击任务的一种作战方式。国内外关于飞行器协同打击方面的研究,目前主要集中在匀速或速度可控的无人机与战术导弹上[1-4],以及关于助推滑翔高超声速导弹再入制导上[5-10]。针对大气层外的协同需求,主要集中在协同拦截上[11-15],也有一些关于弹道导弹协同的研究与探讨[16-19],还有一些关于固体运载火箭入轨的多约束制导[20-21]的研究可供参考。文献[1]为解决机动目标状态不确定的问题,设计扩张状态观测器来估计机动目标的状态,并利用李雅普诺夫稳定性理论进行分析,给出了系统一致收敛时间。文献[2]考虑协同探测效能,利用有限时间控制理论,提出了考虑探测构形的协同制导方法。文献[3]针对无向通信拓扑的机动目标,提出了一种分布式协同制导策略,实现角度约束的同时攻击。文献[4]采用“领弹-从弹”结构,提出了一种跟随者与领导者保持一致时间的协同制导律。文献[5]从可达域覆盖集的角度出发,提出了一种拦截弹机动能力弱于目标情况下的协同拦截策略。文献[8]在此基础上将场景扩展到三维空间中,提出了一种合作覆盖策略。文献[6]针对高超声速飞行器再入大气层,考虑攻角和时间约束提出了一种协同制导律。文献[7]针对助推滑翔高超声速再入导弹速度不可控的特点,提出了一种通过调整速度前置角来实现时间协同的方法。文献[9]采用固定时间控制技术与“领弹-从弹”结构,提出了一种三维协同制导律解决约束攻击角度条件下的同时到达问题。文献[10]面对高超声速飞行器再入协同飞行需求,提出了一种基于序列凸优化的协同再入轨迹规划方法。文献[11]针对大气层外多弹协同拦截问题,提出了带故障诊断的协同跟踪算法、时间协同中制导律与末制导律。文献[12]针对导弹拦截目标问题,应用微分对策理论,研究了有限时间微分对策制导律,满足了末端约束并实现闭环系统稳定。文献[13]针对多枚拦截器对单目标的拦截问题,提出了一种零控脱靶量两侧逼近的协同拦截策略。文献[14]针对多拦截器角度协同制导的问题,基于微分对策理论,推导出角度时间协同制导算法。文献[15]针对固定末端时刻拦截机动目标的制导系统,建立了非线性有限时间微分对策框架,通过自适应动态规划算法获得了近似最优函数与最优控制策略。文献[16]针对弹道导弹突防技术现状及智能化发展进行了探讨,对集群协同的关键技术进行了分析。文献[17]采用GA-BP模型对弹道导弹协同突防效能进行评估。文献[18]基于多枚弹道导弹的空中动态组网技术,提出了几种多弹协同规划的作战应用方法,为弹道导弹协同作战规划提供了思路。文献[19]针对弹道导弹多弹协同攻击目标的问题,提出了一种满足最小末速约束下指定攻击时间的协同飞行策略。文献[20]针对固体运载火箭末级多约束制导入轨需求,提出了一种在真空段具有速度管控能力的多约束制导方法。文献[21]针对固体火箭耗尽关机的制导问题,设计了一种能量管理制导方法,在满足速度和位置的约束下实现多余能量的消耗。然而弹道导弹动力学特性与无人机以及战术导弹存在很大差异,弹道形式、状态约束以及机动方式均存在显著不同,这些差异使得战术武器的多弹协同方法与约束制导方法难以直接满足弹道导弹多弹在大气层外的协同需求。
因此,本文针对大气层外弹道导弹时间协同需求,开展大气层外固体发动机耗尽关机的弹道飞行时间控制方法研究。首先,针对弹道导弹末级采用无推力终止的固体发动机,考虑推力大小无法调节与被动关机的特点,设计导弹增速方向交替变换规律,实现固体发动机能量管理。然后,推导能量管理对终端状态造成耦合影响的解析式,设计耗尽关机的制导律,对能量管理造成的耦合影响进行了修正补偿,使各导弹发动机关机时刻速度矢量与位置矢量达到满足飞行时间约束与位置约束的零控状态。最后,进行了不同制导算法对比验证以及同地/异地同时/不同时发射情况下的多弹时间协同仿真验证。
1 耗尽关机制导问题描述
弹道导弹时间协同作战的核心问题是导弹弹道的飞行时间控制,而约束大气层外飞行时间需要在三级闭路制导阶段实现。由于大气层外没有气动力的影响,导弹在三级发动机关机后就进入了无动力的惯性滑行阶段,因此需要使发动机关机时刻的速度矢量与位置矢量达到满足飞行时间约束与位置约束的零控状态,才能实现大气层外飞行时间控制。由于固体弹道导弹采用耗尽关机这种模式,其发动机产生的总视速度模量是一定的,因此为了满足导弹飞行弹道的位置约束与时间约束,需要通过能量管理算法产生附加姿态变化去消耗多余能量。然而,能量管理过程中的附加姿态变化会对终端状态造成耦合影响,导致交班点时间与位置状态偏差较大。典型弹道导弹飞行弹道示意如图1所示。
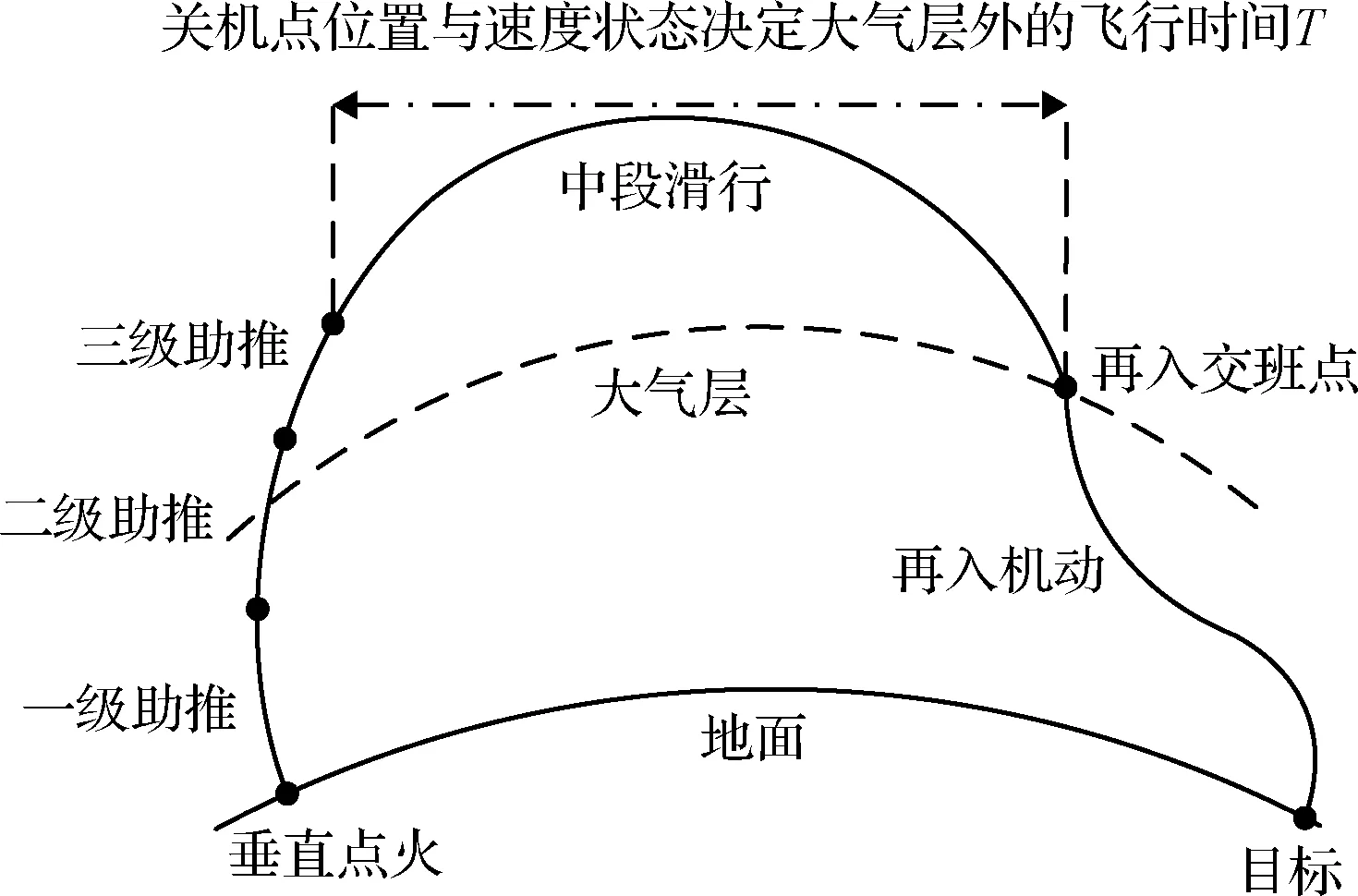
图1 典型弹道导弹飞行弹道
2 带能量管理的时间控制制导律设计
对于弹道导弹而言,若想实现大气层外时间协同需求,需要对弹道的飞行时间进行严格约束。根据轨道动力学原理[22],如果已知导弹在空间中两点K,HP的位置矢量rK,rH以及规定的飞行时间TC,则可以确定连接两点的飞行弹道,以及弹道上任意一点的位置和速度。因此,导弹飞行时间的控制问题可以转换为导弹速度矢量的控制问题,当导弹的速度矢量达到需要速度矢量时,便能达到对飞行时间进行控制的效果。受限于篇幅,本文不给出约束飞行时间的需要速度具体求解方法,可参考文献[22-23]进行推导。固体发动机为了结构简单以提高可靠性,通常不会配备推力调节装置与推力终止装置,只能采用耗尽关机方式,这使得制导算法必须考虑发动机提供的速度增量与需要速度之间的匹配关系。
2.1 耗尽关机能量管理问题
能量管理本质是通过控制推力矢量与待增速度矢量之间的夹角来消耗多余的视速度模量,使得导弹在增速过程中视速度模量到达WM时,导弹速度增量为Vg,而导弹速度恰好达到需要速度VR,K。为了便于能量管理过程的描述,在导弹需要速度计算点OK处建立速度控制坐标系OK-Γεη,其中Γ为待增速度矢量方向,ε为速度控制方向,η轴与Γ轴、ε轴构成右手坐标系,附加姿态角在平面OK-Γε内进行变化,其示意图如图2所示。
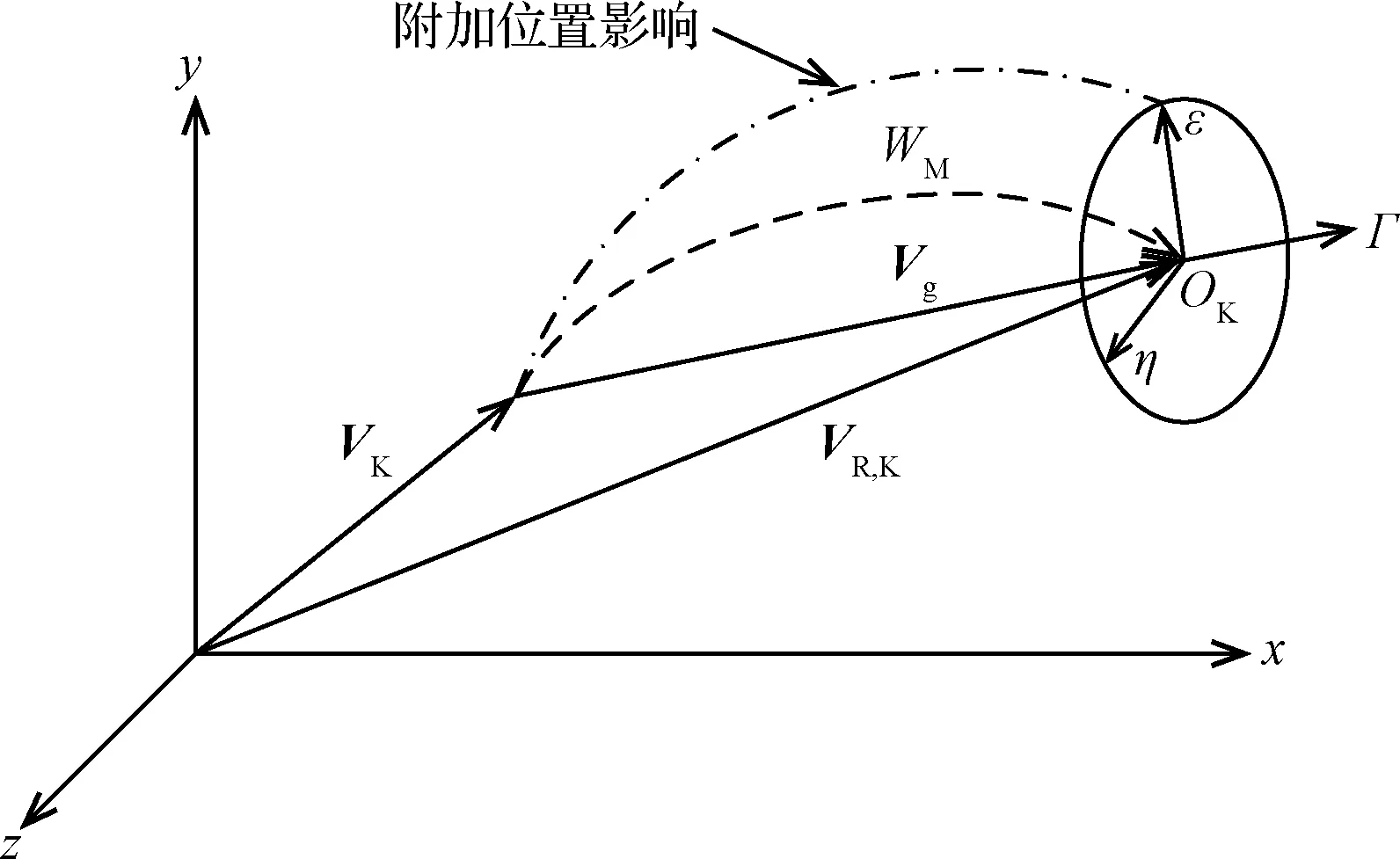
图2 能量管理算法原理示意图
在速度控制面OK-Γε内微分方程组为
(1)
式中:vΓ,vε为Γ与ε方向上的速度;uem(t)由能量姿态模型产生;rΓ,rε为Γ与ε方向上的位置;T为发动机推力;m为导弹当前质量。
由于导弹增速过程中存在位置矢量的变化,以及能量管理过程中交变姿态会产生附加位置量,这些附加的位置变化量会对终端状态产生耦合影响,造成制导精度的下降,因此要在需要速度求解过程中考虑耦合影响并对其进行抑制。
2.2 交变姿态能量管理模型设计
本文拟采用交变姿态能量管理模型(AEM),通过附加姿态角的正负变换实现能量管理,同时使得在ε方向上产生的速度分量相互抵消,模型设计的附加姿态角变化规律如图3所示。
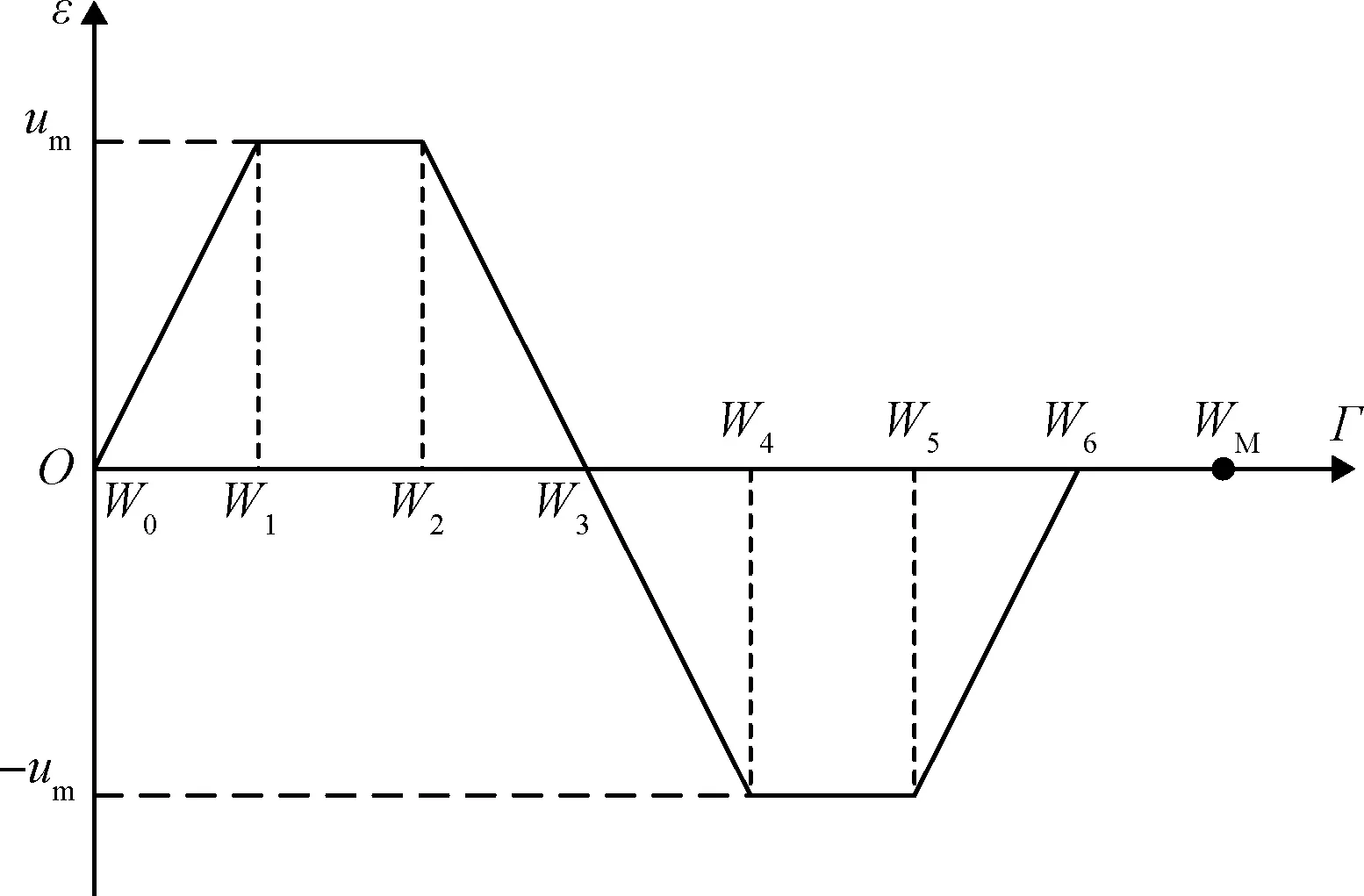
图3 交变姿态模型的姿态角变化规律示意图
将发动机的总视速度模量WM分为两个部分:第一部分(W0~W6),通过交变姿态实现能量管理;第二部分(W6~WM),采用定轴飞行保持稳定,避免因发动机秒耗偏差造成模型尾段姿态角速率过大的问题。姿态角变化的数学模型如式(2)所示:
(2)

2.3 能量管理耦合影响的解析推导与验证
由于导弹增速以及能量管理过程中产生的附加位置量会对终端状态造成耦合影响,进而造成制导精度下降。为更好地补偿耦合影响,提高制导精度,需要对这些耦合影响进行分析推导。
由式(1)与式(2)可以得到能量管理过程中Γ方向与ε方向上的速度量为

(3)

(4)
式中:t*为时间积分变量;W*为视速度积分变量。
将式(2)代入式(3)与式(4)进行分段函数积分可以得到关于vΓ(W)与vε(W)的解析解。由于uem(W)为分段函数,因此在进行每一段积分时,需要将上一段的结果代入,即
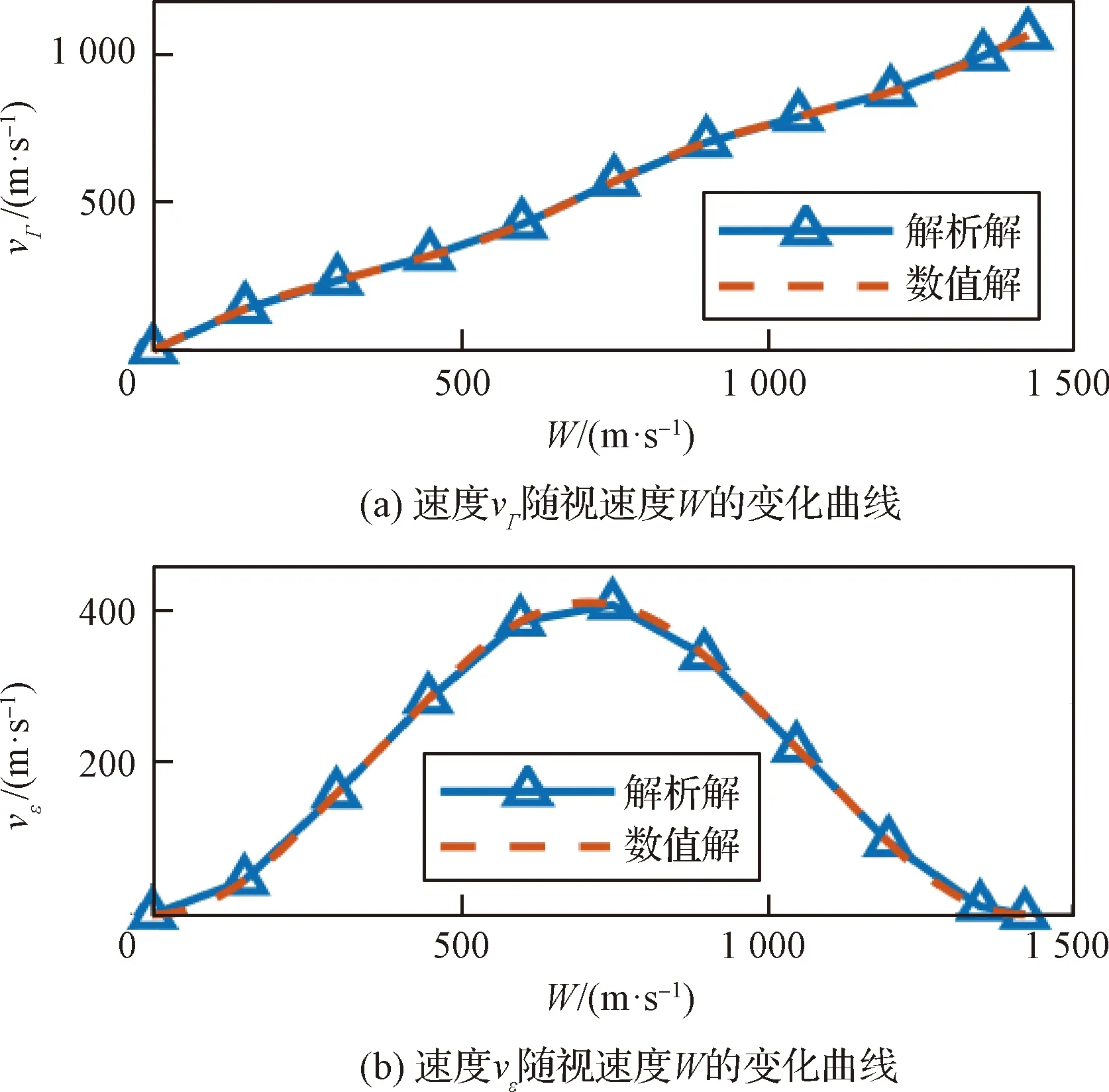
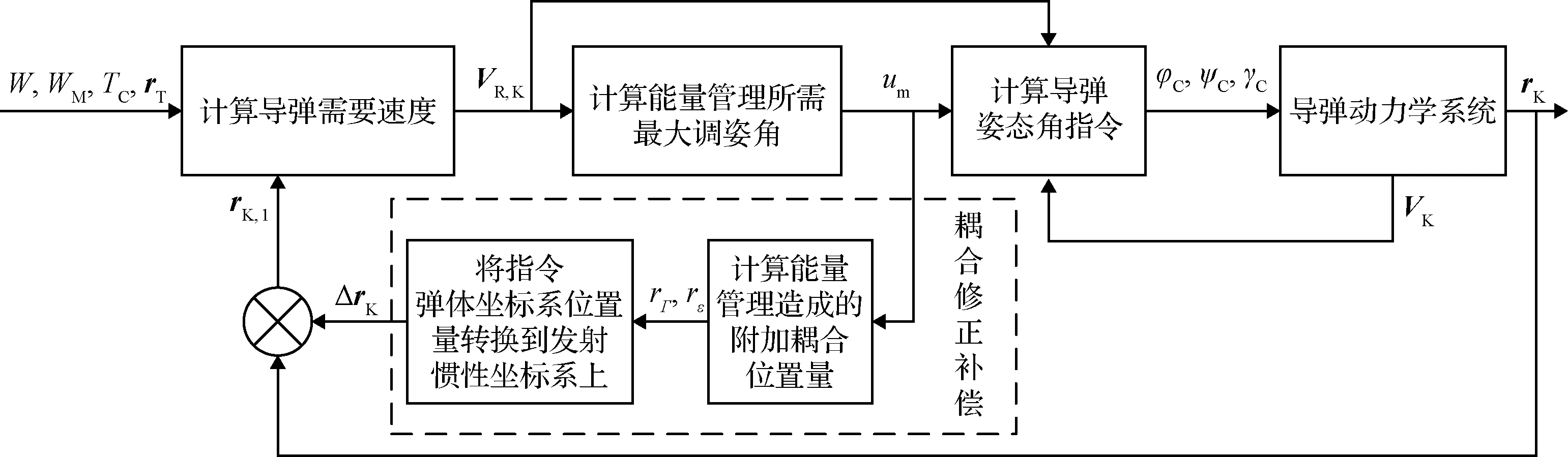
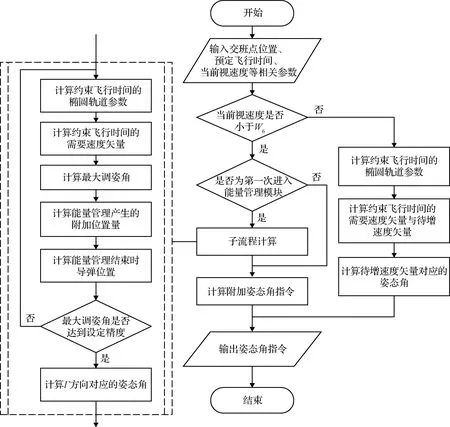
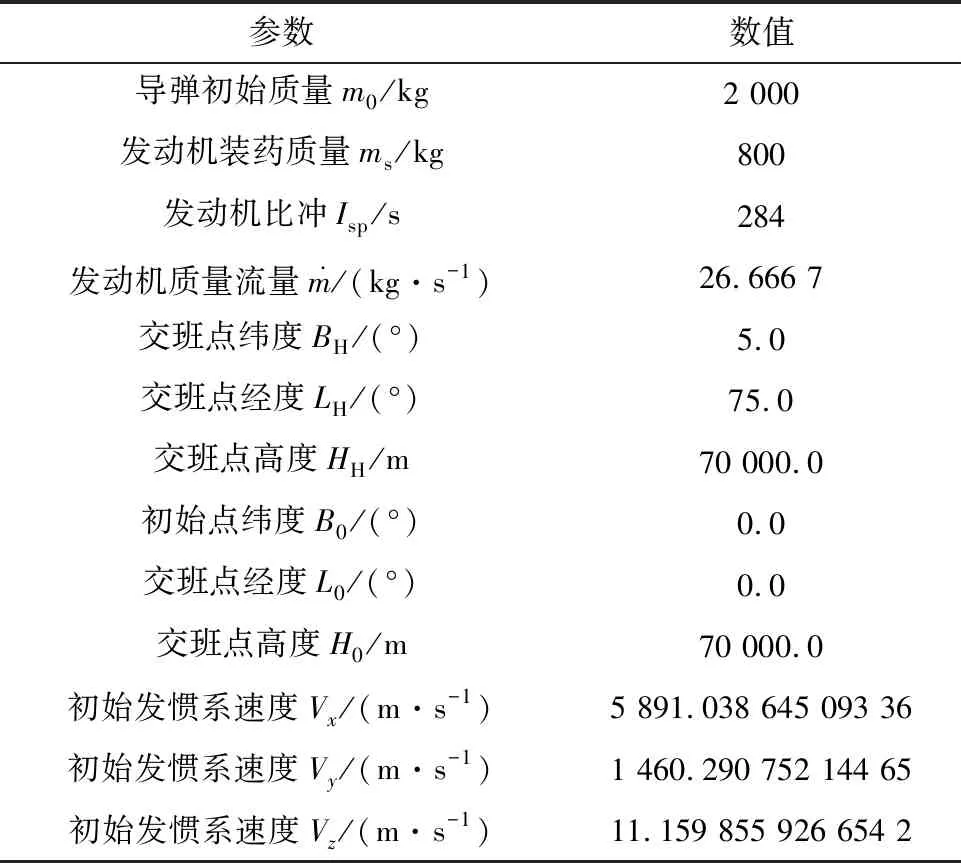
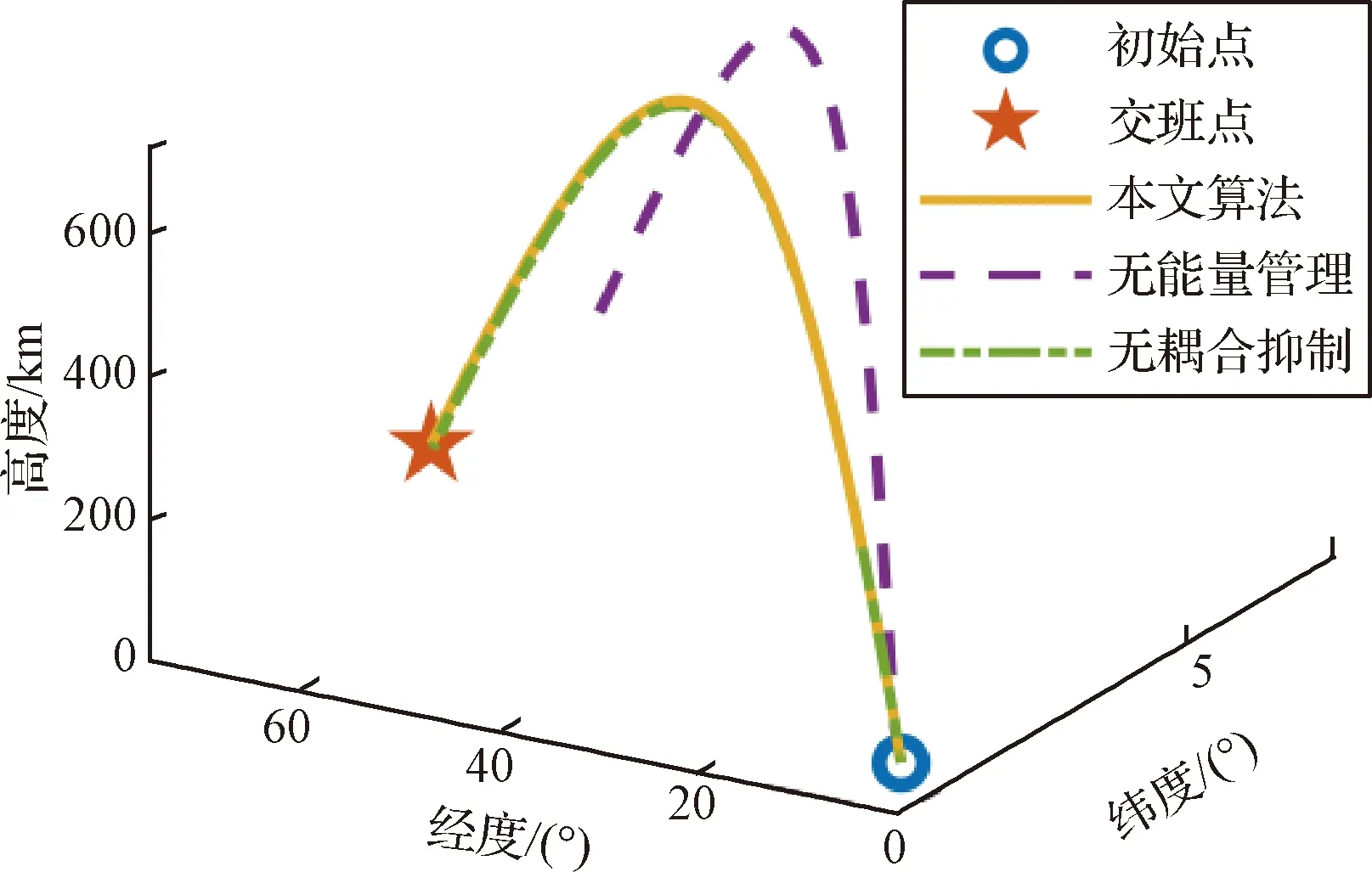
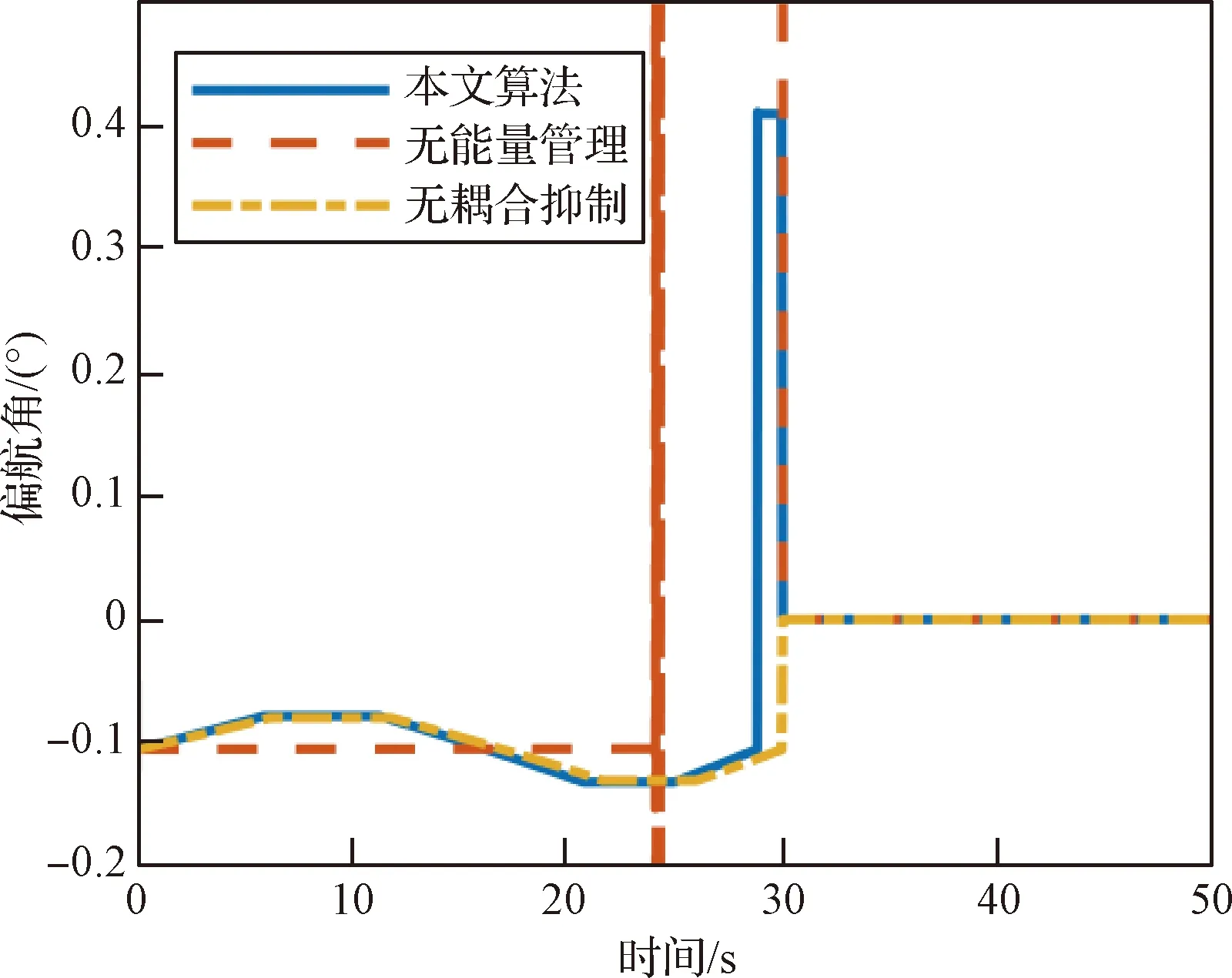
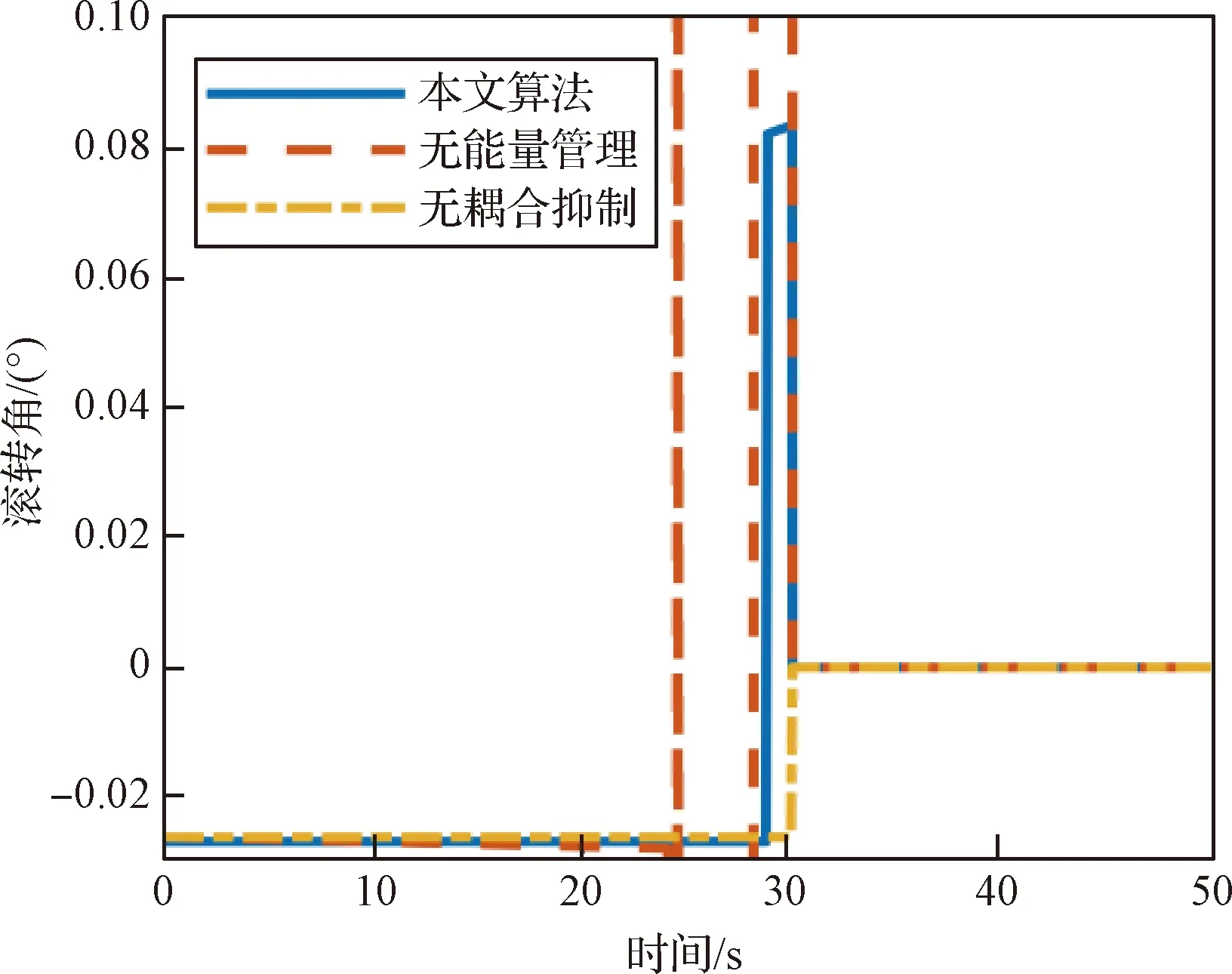
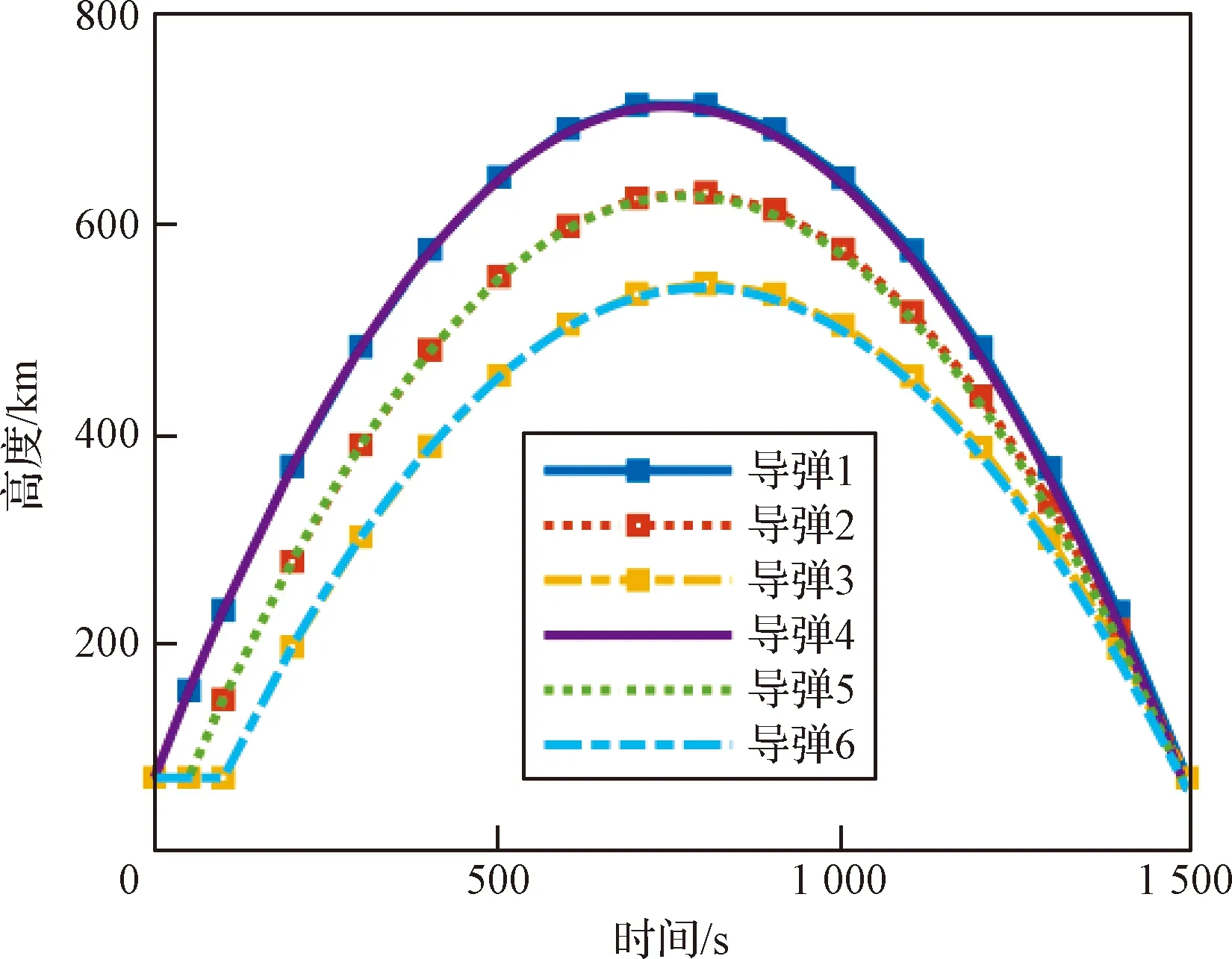
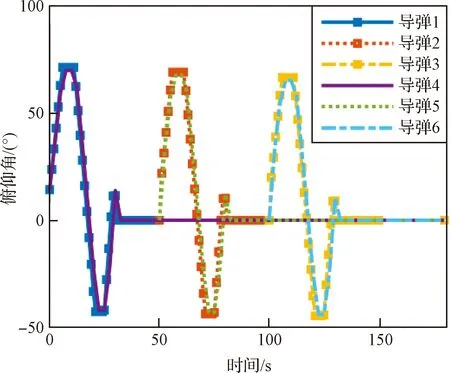
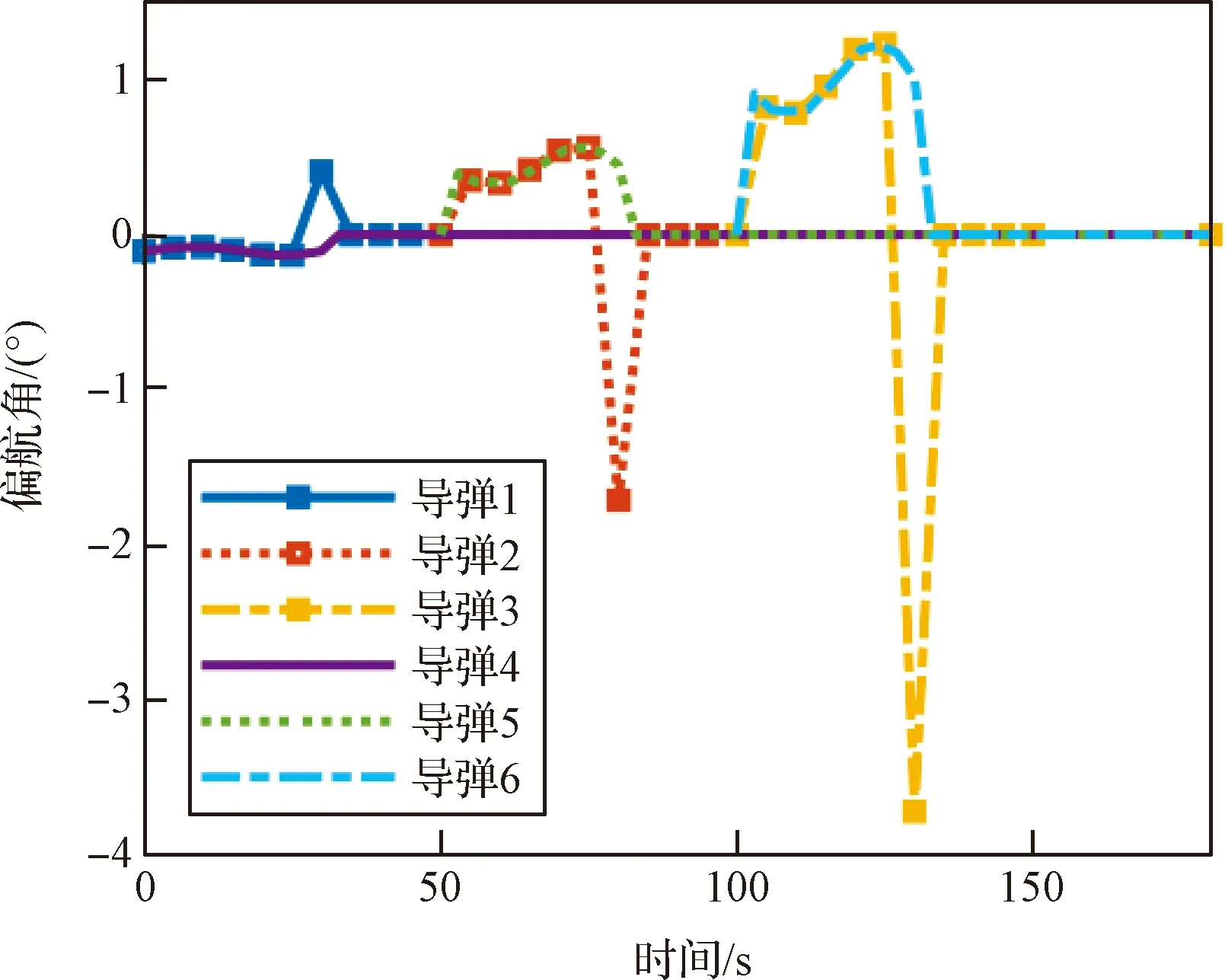
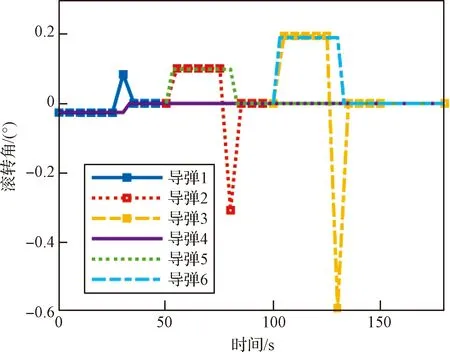
(1)W0≤W (5) (2)W1≤W (6) vΓ(W)的W2≤W 对Γ方向与ε方向上的速度进一步积分可以得到能量管理过程中Γ方向与ε方向上的位置量为 (7) (8) (9) 通过式(9)对式(7)与式(8)进行换元得到 (10) (11) 将vΓ(W)与vε(W)的解析式代入式(10)与式(11),进行分段函数积分,其推导过程与式(5)和式(6)对vΓ(W)的推导过程类似,这里不再赘述,最终可得到关于rΓ(W)与rε(W)的解析解。 为验证能量管理过程中,因交变姿态产生Γ方向与ε方向上的速度量与位置量解析解推导结果的正确性,利用数值积分法与解析法分别进行计算,以数值积分解为标准值,解析解与标准值之差为解析法误差,对解析解推导结果进行对比验证,结果如图4~5和表1所示。 表1 速度与位置的解析解精度 图4 速度vΓ与速度vε随视速度W的变化曲线 从图4可以看出在速度曲线vΓ与vε上解析解与数值解重合,从图5可以看出在位置曲线rΓ与rε上解析解和数值解重合。从表1可以看出,速度解析解精度可达到10-5~10-6m/s量级,位置解析解精度可达到10-4~10-5m量级。上述内容验证了能量管理耦合影响解析式推导的正确性,为后续补偿耦合影响提高制导精度奠定了基础。 图5 位置rΓ和位置rε随视速度W的变化曲线 (12) 参考弹体坐标系到发射惯性坐标系转换矩阵[24]与矩阵(12)可以求出Γ方向对应的姿态角: (13) ψΓ=-arcsinc13 (14) (15) (16) 式中: (17) (18) 传统闭路制导理论[22-23]根据导弹当前位置矢量rK、交班点位置矢量rT以及一个轨道约束条件(关机点速度倾角或交班点速度倾角或轨道飞行时间),便可实时计算出导弹当前的需要速度矢量VR,K,再利用导弹需要速度矢量VR,K、当前速度矢量VK以及导弹当前视速度W,进一步计算出导弹姿态角指令。带有能量管理的闭路制导算法则是在导弹姿态角指令上附加一个消耗多余能量的附加调姿角实现的。 本文的创新之处在于,在闭路制导算法基础上利用导弹能量管理的姿态角变化的数学模型和最大调姿角计算出能量管理造成的附加耦合位置量,得到发动机关机时刻的位置矢量,并用其计算导弹需要速度矢量,形成制导系统的闭环反馈,通过对位置矢量进行修正补偿,进而抑制耦合影响,实现对飞行时间的精确控制。其飞行时间控制的闭环反馈制导系统框图如图6所示。 图6 飞行时间控制的闭环反馈制导系统框图 通过上述分析推导得到了关于时间约束条件下的椭圆轨道参数与需要速度矢量,可以将导弹飞行时间的控制问题转换为导弹速度矢量的控制问题。同时针对导弹速度矢量控制问题,推导出了交变姿态耦合影响解析式以及姿态角指令确定方法。综上,本文所提的飞行时间控制方法的各个环节的相关量均已求出,时间控制算法详细实施流程图如图7所示,具体步骤如下: 图7 带能量管理的时间控制算法流程图 (1)确定约束飞行时间的椭圆轨道参数:根据交班点位置、导弹当前位置以及设定的飞行时间计算椭圆轨道参数。 (4)计算能量管理交变姿态造成附加位置量rΓ与rε:根据最大调姿角um与最大视速度增量WM计算附加位置量rΓ与rε。 (5)计算能量管理结束时导弹在发惯系下的位置:根据待增速度矢量Vg,通过式(12)计算发射惯性坐标系到指令弹体坐标系的转换矩阵[cij];根据转换矩阵[cij]将产生的附加位置量rΓ与rε转换到发射惯性坐标系下并加上导弹当前位置坐标得到能量管理结束时导弹在发惯系下的位置。 (6)迭代更新最大调姿角um:采用导弹在能量管理结束时的位置重复进行(1)至(5)流程,当最大调姿角um达到预定精度时退出迭代。 (7)计算Γ方向对应的姿态角:根据待增速度矢量Vg,通过式(13)至式(15)计算待增速度矢量Vg方向所对应的姿态角。 (8)计算附加姿态角指令:根据待增速度矢量Vg、地球引力g以及当前视速度W,通过式(2)、式(16)至式(18)计算附加姿态角指令。 为了验证本文提出的时间控制算法的有效性,将对本文所提出的飞行时间控制算法、无能量管理的闭路制导算法以及有能量管理无耦合影响抑制的制导算法分别进行仿真对比。仿真设定飞抵交班点的时间为1 500 s,仿真初始条件详见表2,数值积分采用龙格—库塔积分方法,积分步长0.001 s。 表2 仿真初始点弹道参数 从图8~11可以看出,采用无能量管理的闭路制导算法,其姿态角指令在制导后期出现了发散现象,从图8可以看出制导指令的发散使得弹道轨迹与其他算法相比产生了非常大的偏差,从表3可以看到具体偏差达到了300 km左右,飞行时间存在1 s左右的偏差。而带能量管理的制导算法,其交班点偏差要显著小于无能量管理的制导算法,且制导后期没有出现姿态角指令发散现象。以上结果表明,对于耗尽关机的固体弹道导弹来说,在制导律中引入能量管理算法是必须的,否则制导律无法适应固体弹道导弹耗尽关机的工作特性。 表3 飞抵交班点时的位置偏差与时间偏差 图8 弹道曲线 图9 俯仰角随时间变化曲线 图10 偏航角随时间变化曲线 图11 滚转角随时间变化曲线 从表3可以进一步看出,引入能量管理但不考虑能量管理过程对终端状态耦合影响的制导算法,其位置偏差在10 km左右,时间偏差在2 s左右,该位置偏差与时间偏差水平无法满足多弹时间协同需求,这表明能量管理过程中终端状态的耦合影响是不可忽略的。而本文提出的弹道飞行时间控制算法考虑了能量管理过程对终端状态的耦合影响,通过推导其耦合影响的解析式,在算法中对耦合影响进行预测并进行有效的补偿修正,使其仿真结果的位置偏差在20 m左右,时间偏差在1 s以内,该结果验证了本文提出的耗尽关机条件下时间控制算法的有效性。 为了进一步验证上述时间控制算法的有效性,以6枚导弹进行异地不同时发射为例,其中前3枚采用本文提出的算法,后3枚采用带能量管理的闭路制导算法。前3枚每枚初始纬度间隔5°,每枚初始时间间隔50 s,后3枚与前3枚的初始仿真条件一致,采用装订形式的静态时间协同,各弹设定飞抵交班点的时间为1500 s,对其进行验证。仿真初始条件详见表4。 表4 仿真初始点弹道参数 从图12~13可以看出由于异地不同时发射,为了同时飞抵交班点,三种初始条件不同的弹道在空间中呈现高中低规律分布,其中飞行时间最长的弹道最高,飞行时间最短的飞行弹道最低,本文算法与能量管理闭路制导算法在弹道曲线上存在一定差异,但整体变化规律类似。从图14~16可以看出在能量管理阶段,俯仰角与偏航角按设计的交变姿态模型进行了相应的姿态角变化,与弹道曲线的规律类似,两种算法存在一定差异,但整体变化规律相近。从表5可以看出,采用本文算法的3枚导弹在交班点的位置偏差范围均在20 m左右,飞行时间偏差均在1 s以内,而采用能量管理闭路制导算法的3枚导弹在交班点的位置偏差范围在10 km左右,飞行时间偏差在2 s左右。以上结果表明,本文提出的弹道飞行时间控制算法相比能量管理闭路制导算法拥有更好的位置控制精度以及时间控制精度,本文算法能够对能量管理造成的耦合影响进行有效抑制,并满足导弹异地不同时发射情况下的静态时间协同需求。 表5 飞抵交班点时的位置偏差与时间偏差 图12 弹道曲线 图13 高度随时间变化曲线 图14 俯仰角随时间变化曲线 图15 偏航角随时间变化曲线 图16 滚转角随时间变化曲线 本文针对大气层外导弹时间协同需求,开展耗尽关机的弹道飞行时间控制算法研究,实现了大气层外固体弹道导弹耗尽关机条件下的多弹时间协同。主要结论如下:1)所提算法解决了不引入能量管理的传统闭路制导会出现的发动机工作末期制导指令发散现象;2)所提算法考虑了传统俯仰偏航通道的能量管理方法所忽视的耦合影响,降低了交班时刻的位置偏差与时间偏差;3)推导出了能量管理对终端状态造成耦合影响的解析式,并设计了相应的飞行时间控制算法对耦合影响进行补偿修正,仿真结果验证了算法的有效性;4)所提算法可以有效满足固体弹道导弹在异地不同时发射情况下大气层外弹道的时间协同需求。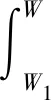
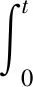
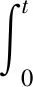
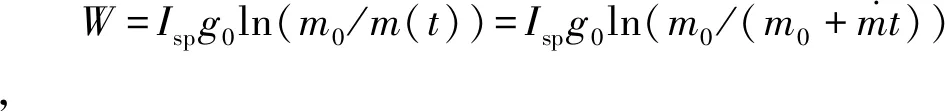


2.4 制导姿态角指令的确定
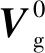
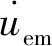
2.5 时间控制算法求解流程


3 仿真校验
3.1 不同制导算法仿真结果对比


3.2 异地不同时发射弹道时间协同仿真



4 结 论

