近似数量系统对数学困难儿童数学能力的影响

李烨 李婷 李蓉 邵秀巧

摘要 近似数量系统是心理学中一个较为新兴的研究领域，它是人类基本数感不可或缺的一部分。为探究提升数学学习困难儿童数学能力的有效路径，本研究以石家庄市2所同质小学二、三、四、五年级数学学习困难儿童为研究对象，调查小学数学学习困难儿童近似数量系统与数学能力之间的关系，并进行干预训练。研究结果发现：数困生近似数量系统敏锐度与数学能力存在显著关联。对近似数量系统进行为期10周20次的训练后，训练组数困生的近似数量系统敏锐度和数学学习能力均得到提升，控制组数困生的近似数量系统敏锐度和数学学习能力训练前后无显著差异。近似数量系统的训练可改善数学学习困难儿童的数学能力。

关键词 数学学习困难儿童；近似数量系统；数学能力

中图分类号：G612文献标识码：ADOI：10.16400/j.cnki.kjdk.2023.11.050

数学学习困难（以下简称“数困”）指的是儿童智力正常，因数学能力的缺损而导致的学生在数学学习上落后于同年龄或同年级的一般水平[1]。已有研究主要从领域一般性和领域特殊性的角度对造成儿童数学学习困难的原因进行研究，很多研究集中于领域一般性因素，研究认为数困生执行功能的抑制、刷新和转换功能缺陷是造成数学学习困难的主要原因[2-4]。而从领域特殊性的角度来看，儿童出现数困是因为在数字加工过程[5]和数字感知能力[6]等方面存在缺陷。其中，数量表征系统中的近似数量系统会影响儿童的数字加工和数字感知能力[7]，因此，数困生数量表征方面的缺陷可能和近似数量系统有关。本研究从领域特殊性的角度，通过对数困生进行近似数量系统的干预训练，探讨提升数困儿童数学能力的有效路径。

1近似数量系统与数学能力的研究现状

近似数量系统（以下简称“ANS”）是心理学中一个较为新兴的研究领域，它是人类基本数感不可或缺的一部分。近似数量系统是个体在不需要依赖计算和数量符号的情况下，对一组数量进行近似表征的系统，具有不精确性和近似性[8]。例如，看到一群人时，个体可以一个一个精确地数出来，这种能力属于精确数量系统；又或者在很短的时间内快速估算出它的数量，这种能力就属于近似数量系统。

近似数量系统是与生俱来的，人类和动物都具有，而且近似数量系统敏锐度随年龄增长不断提高[9]。Inglis等人（2011）的研究表明儿童的近似数量系统精确度与数学成就测验分数呈显著正相关[10]。Libertus等人（2013）以学前儿童为被试，发现学前儿童之后的数学成绩与近似数量系统的精确度息息相关，近似数量系统对今后的数学成绩有一定的预测作用[11]。另外，Mazzocco等人（2011）通过比较计算障碍儿童和正常儿童，发现计算障碍儿童的近似数量系统敏锐度与正常儿童存在差异，前者显著低于后者[12]。同样，Piazza等（2010）发现年龄为10岁的数困儿童的近似数量系统敏锐度相当于5岁正常儿童的近似数量系统敏锐度。虽然大部分研究证明近似数量系统敏锐度与数学能力之间存在显著的相关或因果关系，但仍有部分研究未发现二者的相关关系[13]。

目前衡量个体近似数量系统敏锐度差异的测量指标主要为韦伯系数w，正确率和反应时。点集的数量比较任务是测量被试近似数量系统敏锐度的主要方式。由于近似数量系统训练的任务设计标准不一样，训练效果会出现差异。Hyde等人（2014）通过对儿童进行近似数量系统训练，发现儿童的算术精确性得到了提高[14]。Khanum等（2016）对一年级学生进行了非符号数量任务和非符号大小任务，发现短期的近似数量系统训练能提高符号数学能力[15]。Libertus等人（2020）发现，视觉通道的近似数量系统训练不仅能提高6岁儿童听觉通道的ANS敏锐度，而且可以促进其早期数学能力的发展[16]。

综上所述，数学学习困难学生可能在近似数量系统敏锐度方面存在不足，相应的干预训练对学生的认知发展与学业表现有积极作用。然而，目前关于近似数量系统的训练方案及有效性尚不明确，本研究在探索数困生近似数量系统敏锐度和数学能力关系的基础上，进行相应的干预训练，以期探索提升数困儿童数学能力的有效路径。

2研究方法

2.1被试

被试为小学数学学习困难学生，选自石家庄市2所同质小学二、三、四、五年级。数困生按照以下几个步骤进行筛选，首先，将学生3次语文、数学考试成绩和数学标准化测验成绩转化为Z分数，筛选出语文成绩处于中等及以上水平，而数学成绩位于年级后段25%的学生为数学学习困难学生。之后，对已筛选的数困生进行《瑞文推理测验》，确保智商正常（IQ>90）；同时，排除因动机低下、情绪障碍或家庭原因导致的数学学习困难。符合以上条件的学生为研究对象，结合家长反馈的知情同意书，最后共筛选出数学学习困难学生33人，从33名学生中随机分成2组，1个训练组和1个对照组，近似数量系统训练组17人，控制组16人。

2.2研究工具

②近似数量系统敏锐度通过Panamath（http：//panamath.org）软件点集辨别和点集比较等任务测量。这个软件根据不同的年龄设置不同的点集比较任务，适用的年龄段非常广泛，3―85岁的个体均适用，并且该软件已用于多项相关研究。

2.3训练任务

近似數量系统训练采用E-prime软件编程，对数困生进行非符号数量点阵比较任务、非符号数量点阵相加任务和非符号数量点阵相减任务等训练。各项任务点阵呈现时间1200ms，两个点阵比率均为1.2，1.4，1.6和2.0。

2.4实验程序

①前測阶段，每位被试接受数学能力、近似数量系统敏锐度等任务的测试。

②在干预过程中，近似数量系统训练组17名学生进行一周2次，共10周，20次，每次15―20分钟的近似数量系统训练。训练时间为放学后的托管时间，训练组接受相应训练，控制组不做任何干预训练。

③后测阶段，干预结束后，对学生再次进行数学能力、近似数量系统敏锐度的测试，比较前测、后测结果。

3结果

3.1非数困生和数困生近似数量系统敏锐度和数学能力的差异分析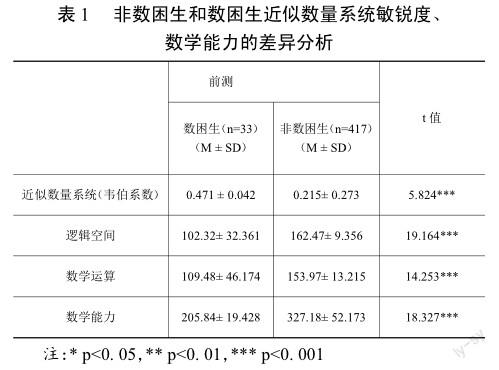

通过表1可以看出，非数困生和数困生在近似数量系统敏锐度和数学能力等方面存在显著差异，非数困生的近似数量系统敏锐度和数学能力都要高于数困生。

3.2数困生近似数量系统敏锐度和数学能力的关系

从上表可以看出，数困生近似数量系统敏锐度与数学能力及其因子存在显著相关关系。近似数量系统敏锐度越好，数困生在逻辑空间、数学运算、数学能力中表现越好。

3.3近似数量系统训练组干预训练效果分析

根据表3可以得出，在前测阶段，训练组和控制组在近似数量系统敏锐度和数学能力等方面均无显著差异。

从表4可发现，训练组的近似数量系统敏锐度和数学能力在干预前后呈现显著差异，近似数量系统干预训练后被试的近似数量系统敏锐度和数学能力均得到提升。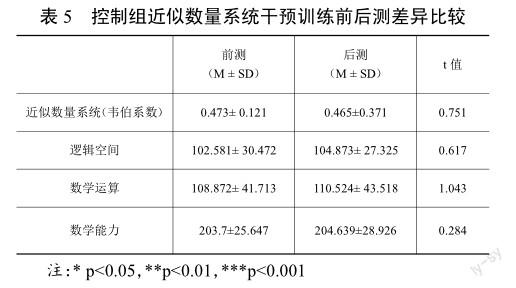

根据表5可以看出，控制组的近似数量系统和数学能力前后测无显著差异。

4讨论

本研究旨在探讨数困儿童近似数量系统敏锐度与数学能力的关系，并在此基础上开展相应训练，以期提升数困儿童的数学能力。通过研究发现，数困儿童近似数量系统敏锐度和数学能力都低于普通儿童，说明数困儿童在近似数量系统敏锐度和数学能力等方面存在不足。同样，Mazzocco等人（2011）通过比较计算障碍儿童和正常儿童，发现计算障碍儿童的近似数量系统敏锐度与正常儿童存在差异，前者显著低于后者。Piazza等（2010）发现年龄为10岁的数困儿童的近似数量系统敏税度相当于5岁正常儿童的近似数量系统敏税度。本研究与前任研究结果相似，数困儿童的的近似数量系统敏锐度要低于正常儿童。另外，无论是数困儿童，还是普通儿童，他们的近似数量系统敏锐度和数学能力存在显著相关关系，即小学生的近似数量系统敏锐度越好，他们的数学能力也就越好。Inglis等人（2011）的研究也表明儿童的近似数量系统敏锐度与数学成就测验分数呈显著正相关。本研究通过为期10周，20次的近似数量系统训练，发现训练组数困生的近似数量系统敏锐度和数学能力均得到提升。正如，Piazza等人（2013）提到近似数量表征不仅会随着年龄不断发展，而且受到后天的环境和教育的影响[17]。Brannon（2013）也指出对个体的近似数量系统进行干预能够改善数学能力。近似数量系统训练有助于提升数学学习困难儿童的近似数量系统的敏锐度和数学能力。

5结论

通过对近似数量系统进行训练，可以提升数学学习困难小学生的近似数量系统敏锐度和数学能力。近似数量系统是很重要的认知机能，它与数学能力之间有着密切又错综复杂的联系。未来应多关注数学困难儿童的认知加工机制，以及干预训练与教学、课后服务的融合，探索提高数困儿童儿童数学能力的有效路径。

基金项目：河北省高等学校人文社会科学研究项目“数学学习困难儿童认知加工特征及干预研究”（SQ2022194）；石家庄市教育科学研究“十四五”规划课题（2021343）；石家庄市高等教育科学研究项目（20201004）。

参考文献

[1]胥兴春.数学学习困难及其心理分析[J].中国特殊教育，2003（3）： 54-57.

[2]蔡丹，李其维，邓赐平.数学学业不良初中生的工作记忆特点：领域普遍性还是特殊性？[J].心理学报，2013，45（2）：193-205.

[3]任偲，蔡丹.执行功能训练对数学学习困难小学生数学能力的促进作用[J].中国特殊教育，2019（6）：63-71.

[4]王恩国，刘昌.数学学习困难与工作记忆关系研究的现状与前瞻[J].心理科学进展，2005，13（1）：39 -37.

[5]Geary，D.C.，Hoard，M.K.，Nugent，L.，&Bailey，D.H.（2012）.Mathematical cognition deficits in children with learning disabilities and persistent low achievement： a five-year prospective study[J].Journal of Educational Psychology，104（1），206.

[6]黎朝钰，肖维婧，赵微.国外数学学习困难干预研究现状与启示[J].现代特殊教育，2021（15）：72-78.

[7]沈龙启越.近似数量系统对中班儿童数感的影响及教育应用[D].金华：浙江师范大学，2021.

[8]Piazza，M.Facoetti， A. Trussardi， A.N. Berteletti， I.Conte，S.Lucangeli， D. Zorzi，M. （2010）. Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia [J]. Cognitive，116（1）， 33-41.

[9]Halberda， J.， Ly， R.， Wilmer， J. B.， Naiman， D. Q.， & Germine， L.（2012）. Numbersense across the lifespan as revealed by a massive Internet-based sample[J].Proceedings of the National Academy of Sciences of the United States of America， 109（28）， 11116-11120.

[10]Inglis， M.， Attridge， N.， Batchelor， S.， & Gilmore， C.（2011）. Nonverbal number acuity correlates with symbolic mathematics achievement： but only in children[J]. Psychonomic Bulletin & Review， 18（6），1222-1229.

[11]Libertus， M. E.， Feigenson， L.， & Halberda， J.（2013）. Is approxim ate number precision a stable predictor of math ability？[J]. Learning& Individual Differences， 25（25），126-133.

[12]Mazzocco， M. M.， Feigenson， L.， & Halberda， J.（2011）. Impaired acuity of the approximate number system underlies mathematical learning disability（dyscalculia）.Child Development， 82 （4）， 1224-1237.

[13]梁笑，康靜梅，王丽娟.个体近似数量系统与其数学能力之间的关系：发展研究的证据[J].心理科学进展，2021，29（5）：827-837.

[14]Hyde， D. C.， Khanum， S.， & Spelke， E. S.（2014）. Brief non-symbolic， approximate number practice enhances subsequent exact symbolic arithmetic in children[J]. Cognition，131（1），92-107

[15]Khanum， S.， Hanif， R.， Spelke， E. S.， Berteletti， I.， & Hyde， D. C.（2016）. Effects of non-symbolic approximate number practice on symbolic numerical abilities in pakistani children[J]. Plos One，11（10），e0164436.

[16]Libertus，M.E.，Odic，D.， Feigenson， L.， &Halberda，J.（2020）. Effects of visual training of approximate number sense on auditory number sense and school math ability[J]. Frontiers in Psychology， 11，2085.

[17]Piazza， M.， Pica， P.，Izard， V.， Spelke， E. S.，& Dehahne，S.（2013）. Education Enhances the Acuity of the Nonverbal Approximate Number System. Psychological Science[J]， 24（6），1037-1043.