非正交斜齿轮系统数学模型及接触特性研究

刘克强

(青海高等职业技术学院公共教学部,青海 海东 810799)

非正交斜齿轮的齿廓通常以点接触啮合,传递着交叉轴齿轮的传动动力,具有较优的传动性能和分扭效果,使得非正交斜齿轮普遍使用在汽车差动机构、直升机减速机、机器人结构、输送机驱动系统等领域[1-2]。

国内外学者对斜齿轮副的接触特性开展了研究。Liu等[3]建立了精确的齿轮副啮合模型,研究了工件夹持装置误差对端面滚齿准双曲面齿轮啮合特性和齿面几何形状的影响。杨主希等[1]基于曲面啮合传动特性,建立了非正交斜齿轮修形齿面模型,推导了接触应力解析方程,通过有限元软件分析了斜齿轮接触应力,结果表明有限元仿真结果与所推导的接触应力结果具有较高的吻合性。李仕轩等[4]通过共轭齿面接触轨迹建立了渐开线斜齿轮副的动力学模型,利用数值分析法进行了仿真模拟,研究了各参数对接触特性的影响关系。马登秋等[5]设计开发了圆弧齿线圆柱齿轮的结构,通过有限元比较分析了该结构与传统齿轮的传动特性,研究表明所设计的圆弧齿轮具有较优的传动性能。朱冬文等[6]建立了轴线偏差的斜齿轮啮合数学模型,该模型考虑了多齿接触对的啮合影响,分析了不同轴线偏差角度对齿轮接触特性的影响规律。陈燕等[7]研究了不同载荷下变齿厚渐开线齿轮齿面接触特性,结果表明轴交角和轴向偏移是影响传动副接触状态的重要因素,该结论为渐开线齿轮传动接触分析提供了参考依据。

基于以上研究成果,本文提出了一种基于曲线接触元件的齿轮传动设计新理论,提出该设计理论的目的是提高交轴斜齿轮传动的承载能力和传动特性,通过建模和仿真的形式研究非正交齿轮副的接触特性,为非正交齿轮副的结构设计提供理论支撑。

1 非正交斜齿轮的数学模型

本文建立的非正交斜齿轮模型如图1所示,固定坐标系为S(O-x,y,z)、Sp(Op-xp,yp,zp),活动坐标系为S1(O1-x1,y1,z1)、S2(O2-x2,y2,z2),变量ω(1)和ω(2)为角速度,φ1和φ2分别为小齿轮1和齿轮2的旋转角度,Σ为两轴的夹角,a为中心距,P为接触点。

图1 非正交斜齿轮空间模型

假设空间曲线Γ1:r1=x1(t)i1+y1(t)j1+z1(t)k1位于坐标系S1,其中r1为坐标系S1中接触点的极坐标矢量,由图2中建立的齿轮副之间的关系,可以得出接触点P处的相对速度为[8]:

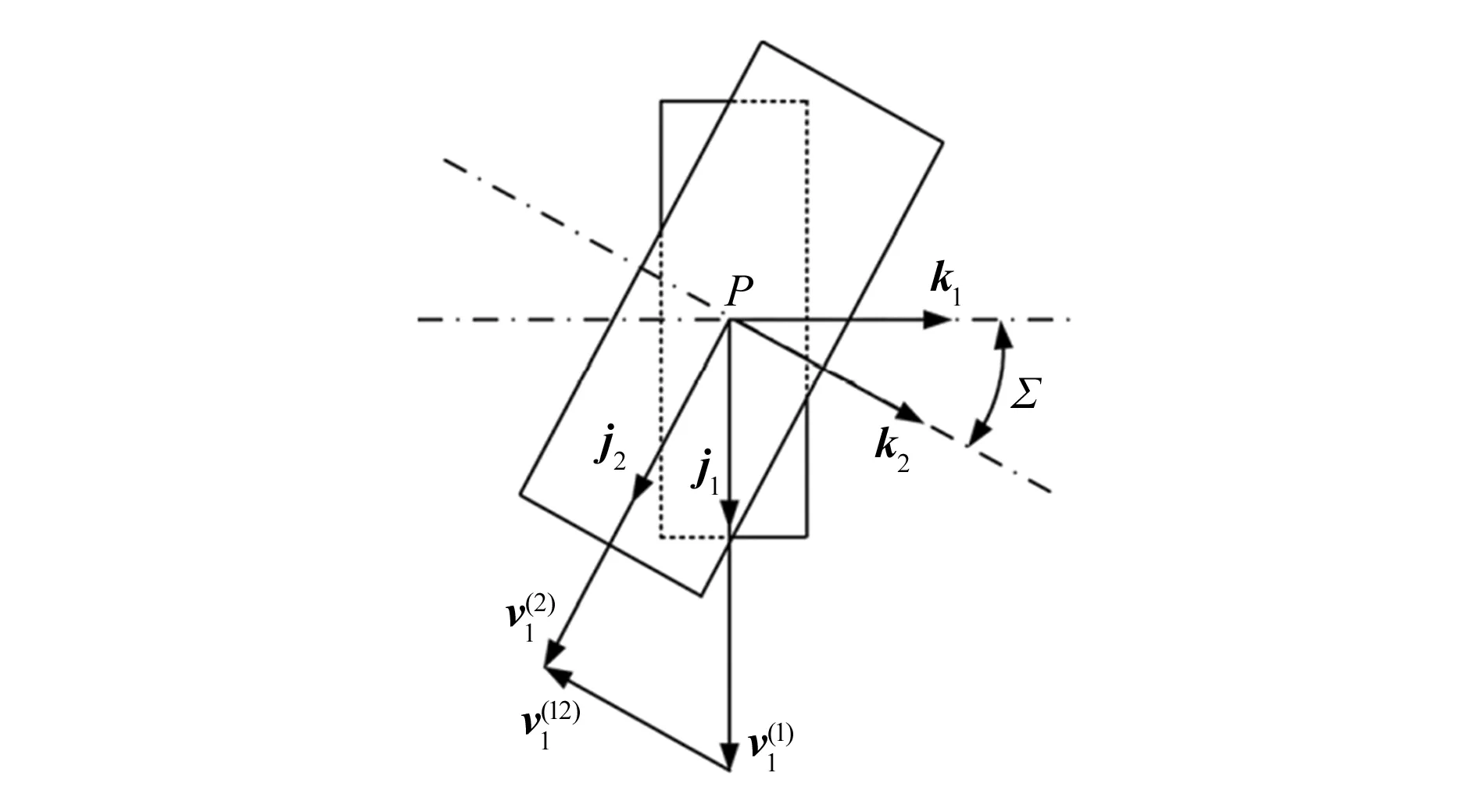
图2 齿轮副之间的空间关系

ai21sinφ1cosΣ]i1+[x1(1+i21cosΣ)+

z1i21sinφ1sinΣ-ai21cosφ1cosΣ]j1+i21sinΣ(x1cosφ1-

y1sinφ1-a)k1

(1)

从图3可以看出,接触点M处的法向量可以表示[9]为nn=unβ+vnγ,变量nβ和nγ分别表示主法向量和副法向量。

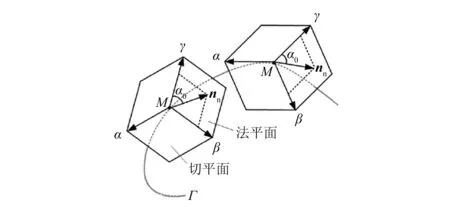
图3 曲线三面体示意图

空间曲线Γ2∶r2=x2(t)i2+y2(t)j2+z2(t)k2,其与空间曲线Γ1共轭,空间曲线Γ2的坐标值可以用式(2)计算:

(2)

式中:x2、y2、z2分别为坐标系S2中的x、y、z方向坐标值,nnx1、nny1、nnz1分别为x、y、z方向的法矢量。

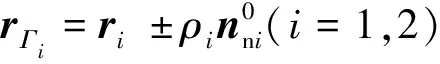
图4 作用面的生成示意图

(3)

由此可以将球体表面表示为rsi(ρicosφcosα,ρicosφsinα,ρisinφ),其中φ∈[-0.5π,0.5π],α∈[0,2π]。

同时根据齿轮顶面和齿根面设计了凸-凹型的齿廓,齿廓的啮合模型如图5所示。

图5 凹凸齿廓的啮合模型

2 非正交斜齿轮副齿廓方程

圆柱螺旋曲线位于小齿轮1上,表述为:

(4)

式中:x1、y1、z1为坐标系S1中的x、y、z方向坐标值,R为节圆半径,θ为空间曲线参数,p为螺旋参数。

式(5)为小齿轮的齿廓方程,式(6)为齿轮的齿廓方程:

(5)

(6)

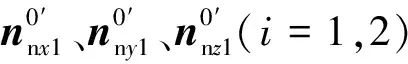
根据表1中的设计参数,利用MATLAB软件计算出数据点结果。图6所示为圆柱螺旋共轭曲线和15°角齿面啮合的简化模型。对齿廓啮合运动进行计算机模拟,齿轮副的啮合过程如图7所示。结果表明,齿轮副以固定传动比连续运转。对于轴向,齿廓以点接触啮合,在齿轮副啮合期间没有啮合干涉。

表1 非正交斜齿轮副基本参数

图6 简化的啮合模型

图7 啮合过程的计算机模拟

3 非正交斜齿轮齿廓特性分析

3.1 根切条件

齿廓的根切现象一般是由于奇点的出现而发生的[11],对于小角度非正交斜齿轮副,由于齿数少,小齿轮容易发生根切。为此本文在研究根切条件后,假设接触区域方程为:

(7)

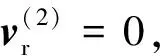
(8)

式中:s为弧长参数;Φ(t,φ,α)为包络条件,Φ(t,φ,α)≡(rt,rφ,rα) = 0。可以确定曲面Σ1上的直线在曲面Σ2上产生奇点,得到:

(9)

(10)

则式(10)存在一个确定的解,从而可以写成:

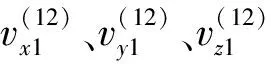
(11)

从而得到管状齿面的根切条件为:Δ1=0,Δ2=0,Δ3=0。

3.2 滑移率

假设具有原始曲线Γ1的主动齿轮将运动传递给具有共轭曲线Γ2的从动齿轮,它们在点K处接触,如图8所示。

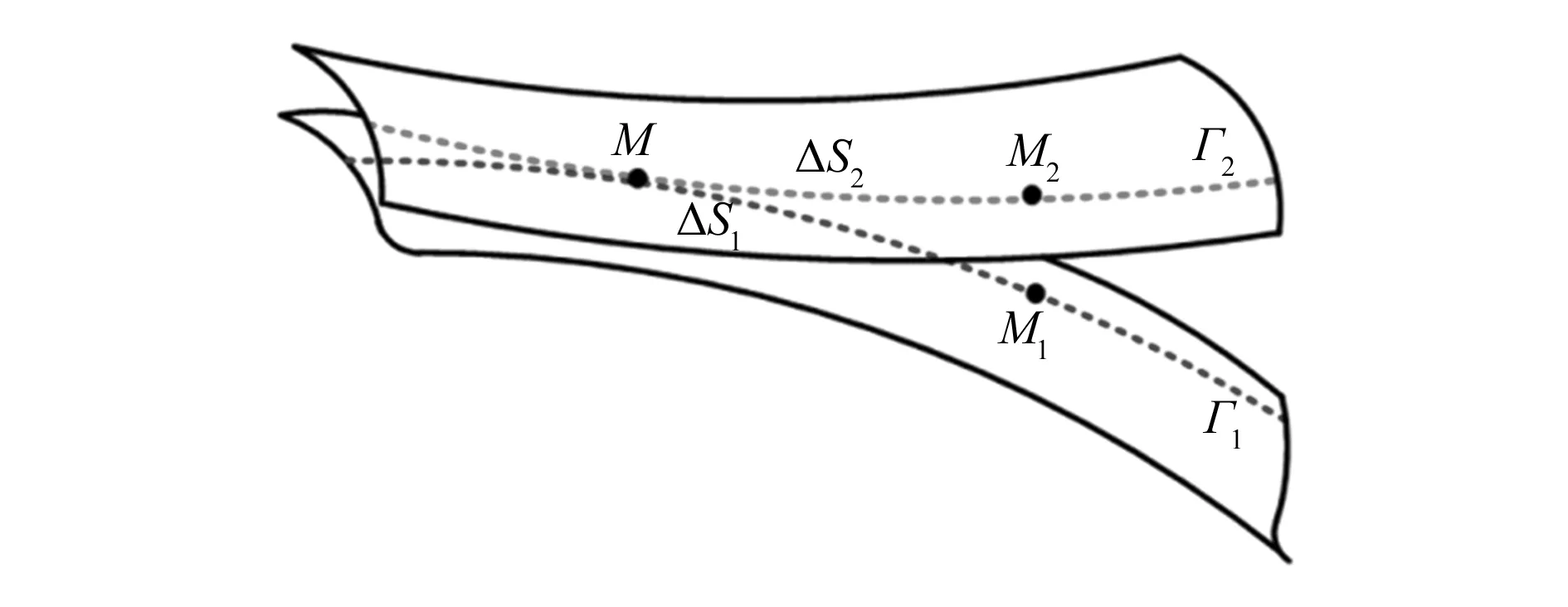
图8 齿廓的滑移示意图

ΔS1和ΔS2分别表示Δt时刻共轭曲线Γ1和Γ2的滑移弧,在啮合过程中趋于零。假设存在相对滑移,弧长MM1与弧长MM2不相等,ΔS1和ΔS2之间的差异称为滑移弧。滑移系数为滑动弧长度与啮合区域内对应弧长度的比值[12]。因此,小轴角非正交斜齿轮副滑移率U1、U2的计算公式为:

(12)

其中:

(13)

根据表1中给定的设计参数,在此基础上计算新齿轮副的滑移比,结果如图9(a)所示。齿轮副的滑移率仅在节点通过零后其正负号发生变化,当两侧附近的接触点开始啮合时,其正负号因滑移速度的方向不同而改变,最大绝对值出现在轮齿啮合的齿根处。同时还计算了相应的横轴渐开线齿轮传动的滑移率,如图9(b)所示。显然,新型非正交齿轮副的滑移率小于渐开线齿轮传动,这有助于提高传动性能。啮合过程可以达到极限位置,理论上可以实现近似纯滚动接触。

图9 滑移率的计算

3.3 应力分析

对齿廓的应力分析可以反映新型齿轮传动的力学性能,共轭齿轮副有限元模型如图10所示,利用ANSYS Workbench软件对模型进行分析。结合实际啮合条件,采用Solid 185六面体单元离散齿轮副。将小齿轮和齿轮的齿廓分别定义为接触面和目标面,分别对应于CONTA 173接触单元和TARGE170单元。

图10 非正交齿轮副的有限元模型

在接触应力分析过程采用赫兹模型[13],利用扩展拉格朗日算法进行求解,整个过程采用MPC184约束单元。模拟选用的材料为20CrMnTi钢,泊松比为0.25,杨氏模量为205 GPa。对小齿轮施加200 N·m的转矩值,新型齿轮副的分析结果如图11所示,最大接触应力为1 266.5 MPa,发生在齿廓中部的接触点,应力沿齿宽方向呈规则椭圆分布,分布区域有向齿根方向扩展的趋势。随着接触面积的增大,接触应力逐渐减小,小齿轮的最大Von-Mises应力为793.69 MPa。

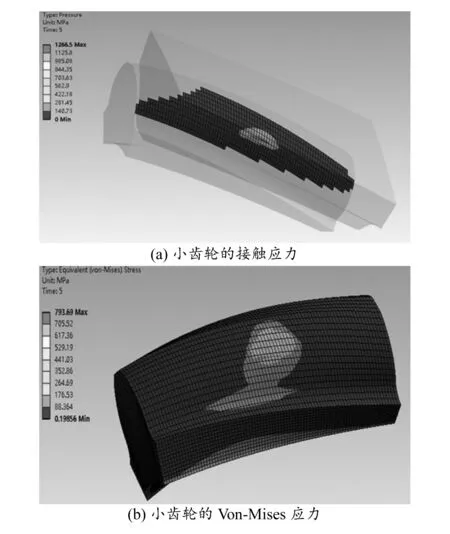
图11 新型齿轮副的应力分析结果

在相同设置下,以渐开线齿轮副为对比对象,其接触状态及有限元分析结果如图12所示。最大接触应力为1 639 MPa,发生在啮合位置,应力沿接触线分布。小齿轮的最大Von-Mises应力为1 233.8 MPa。可以看出新型齿轮副的接触应力明显小于非正交渐开线齿轮传动的接触应力,表明新齿轮副具有良好的接触特性。

4 实验验证

由于齿廓形状的特殊性,本文采用铣削齿轮的方法来加工齿轮副。根据所建立的实体模型,可以实现球头铣刀机床的运动过程仿真,实验过程中的五轴加工中心如图13所示。根据球头铣刀的快速移动和进给功能,工作轴和工作台的旋转功能,可以对齿轮副的曲面进行调整,加工出的小齿轮和齿轮如图14所示。

图13 五轴加工中心

图14 小齿轮和齿轮实物图

对齿轮样机进行性能实验,输入和输出转矩由转矩传感器测量,转速由变速电机控制,齿轮副由加载电机加载。在实验过程中,通过公式η=noTo/(niTi),可以得到齿轮样机的传动效率,其中Ti和ni分别为输入转矩和输入轴转速,To和no分别为输出转矩和输出轴转速。设置速度分别为200、400、600、800和1 000 r/min,施加在齿廓上的载荷分别为200、300、400、500和600 N·m。

给定工况下传动效率如图15所示。由图3可知,提高转速和保持转矩恒定能够提高传动效率。同样地,增加扭矩和保持转速恒定也能提高传动效率。在负载为600 N·m时,最高效率可达95.9%,齿轮样机整体效率为91.2% ～ 95.9%。

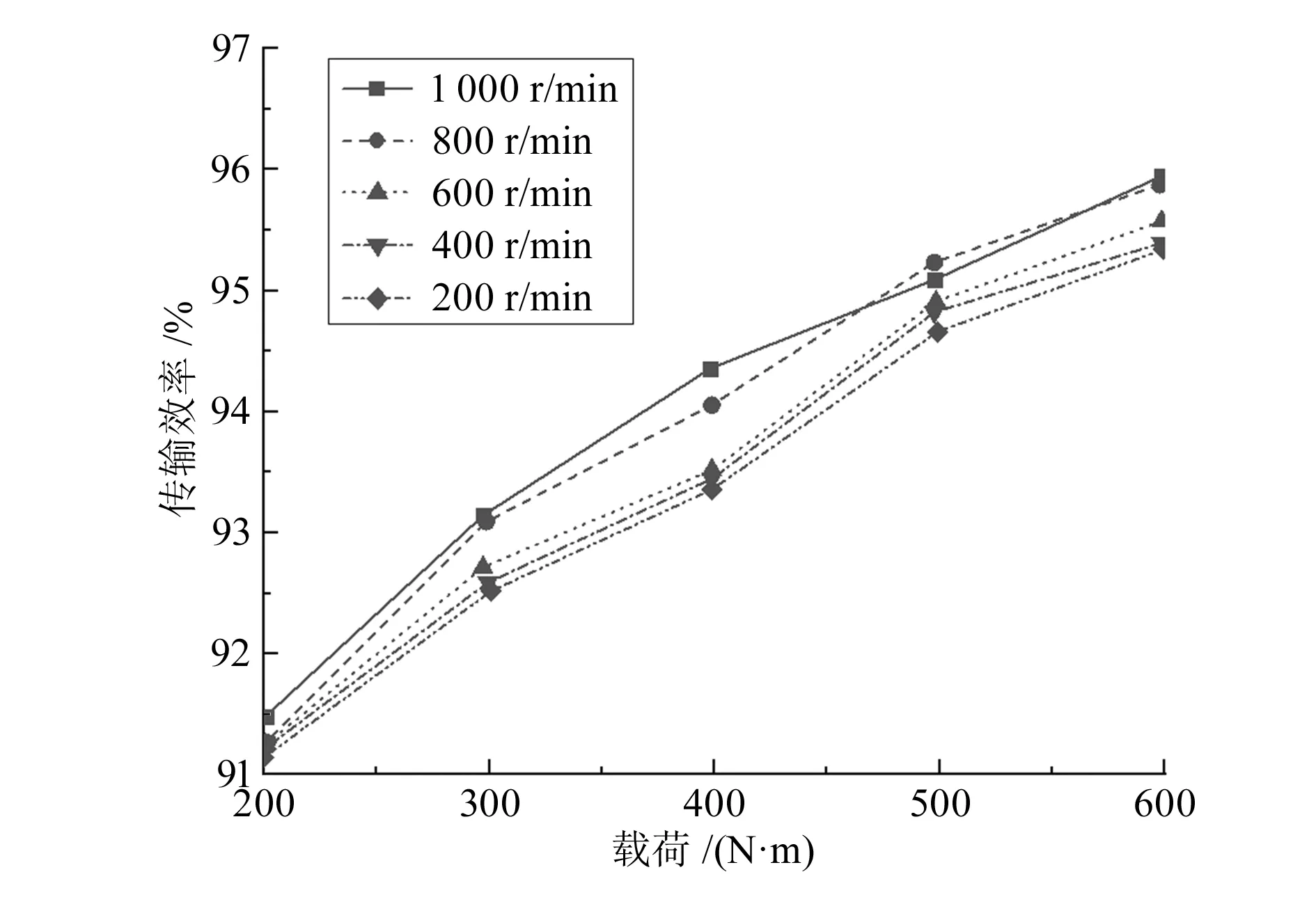
图15 不同转速下新型齿轮副的传动效率对比

5 结束语

本文提出了一种基于曲线接触元件的齿轮传动设计新理论,通过给定的空间共轭曲线建立了齿轮传动的数学模型。根据成形齿廓的奇异条件以及根切问题,推导出成形齿廓的一般方程。根据所得到的共轭曲线,给出了齿廓滑移率的计算方法。在给定的参数下,新型齿轮副的滑动比,小于交轴渐开线齿轮传动的滑动比,有助于提高传动性能。新型齿轮副的接触应力小于交轴渐开线齿轮传动,表明其具有良好的接触能力和强度,验证了所提非正交斜齿轮副模型的合理性。