破除思维定式 明晰概念图像

林品玲　叶诚理

近年來的高考和各地质检中，经常出现三角函数图象与性质中求ω的取值范围问题，通常在选填压轴题位置出现，学生解题中可能存在一定的困难，按照原有的思维定式造往往成求解范围的偏差．如何破除解题障碍，本文就这一类问题学生中产生的常见错误展开分析，并提炼出相应的解题策略，以飨读者．

1.错看函数零点

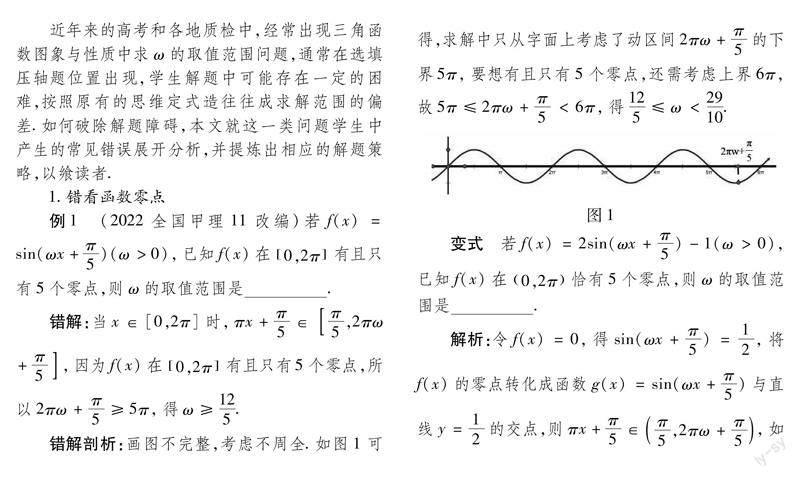
例1 （2022全国甲理11改编）若f（x）=sin（ωx+π/5）（ω>0），已知f（x）在0，2π有且只有5个零点，则ω的取值范围是 .

错解：当x∈［0，2π］时，πx+π/5∈π/5，2πω+π/5，因为f（x）在0，2π有且只有5个零点，所以2πω+π/5≥5π，得ω≥12/5．

通过上述试题的错解分析，我们认为教学中要注重三角函数基础知识的训练，包括熟悉函数图象和性质，树立整体观念，加强数形结合思想、化归转化思想、分类讨论的应用，综合应用方程、不等式进行含参计算，特别是要破除解题中的思维定式，应明晰三角函数的各种概念，培养严谨的治学态度，从中提升学生的直观想象、逻辑推理、数学运算等核心素养.

参考文献

［1］刘明光. 处理三角函数中参数ω问题的基本意识［J］. 中学数学研究（江西师大），2021.（4）：54-58.

［2］姜敏华. 例析三角函数中ω的取值范围［J］. 中学数学研究（江西师大），20219.（8）：45-47.