基于问题为主线的探究式教学

孙强　章建荣

一元线性回归模型是高中数学的一个统计学模型，而“相关系数”是一元线性回归模型中判断线性相关性的一个重要的统计量，其产生过程蕴含着统计学探究的一般思维方式，推导过程中的类比、特殊化等数学思想方法，是培养学生统计学思维、符号运算能力、逻辑推理能力及数据处理思维等素养的落地点.然而，很多教学课在统计量的出现以及公式推导探究过程中并没有很好地体现出“相关系数”这一统计量的必要性以及公式的生成过程，让学生的数学思维得不到良好的发展，难以体现和落实核心素养.基于这些问题，笔者开展了相关的教学设计和教学实践.旨在通过“相关系数”这一统计学概念的教学，探究其在教学过程中自然生成，同时以问题探究为主线，引导学生思考和探索“相关系数”的计算公式，帮助学生体会统计学的探究过程，感悟其中的数学思想，从而营造高效的数学课堂.

一、教学内容分析

“相关系数”是北师大版《普通高中教科书·数学（选择性必修一）》第七章“统计案例”第二节的内容，它既是之前一元線性回归的延续，也是学生学习的第一个统计学模型，对今后的统计学学习具有指导意义.《普通高中数学课程标准（2017年版）》的要求是：①结合实例，了解样本相关系数的统计含义，了解样本相关系数与标准化数据向量夹角的关系.②结合实例，会通过相关系数比较多组成对数据的相关性.因此，本节课的主要任务是了解样本相关系数这一概念为什么会出现，为什么需要相关系数这一统计量，如何研究一个统计模型；其次是如何定义和计算样本相关系数.

二、学情分析

学生已经学过一元线性回归方程，对成对数据的一元线性拟合有了基本的了解.也会利用散点图来观察成对数据是否相关，但是这种对于相关的感知仅仅停留在直观的认知上，而并非在科学意义上的严格计算，对于许多成对数据是否相关，相关性有多大，还没有一个明确的概念.因此本节课应该从学生已有相关性的经验出发，给出直观观察解决不了的问题，让学生感知到相关系数出现的必要性，从而引出冲突，让概念自然生成.

三、教学过程

1.创设情景，引导思考

问题1 给定两个随机变量（x，y）的7组成对数据：（1，0），（4/5，3/5），（0，1），（－4/5，3/5），（－1，0），（－4/5，－3/5），（0，－1），利用最小二乘法，可以得到Y关于X的线性回归方程Y=0.143X+0.102.这时，X和Y是否具有线性关系呢？

教师画出散点图，让学生进行观察，学生容易发现7组成对数据均位于单位圆上，所以X和Y不具备线性关系，用这一组数据建立的线性回归方程无法精确刻画这组数据.

师：对一组数据进行直线拟合之前先应该做什么？

生：先要判断这组数据是否适合进行直线拟合.

师：应该如何进行判断？

生：可以画出散点图直接看所有的点是不是大概在一条直线上.

师：对了，对于数据量较小且散点图较规则的数据确实可以画散点图来进行观察判断，那不妨看看的散点图1及图2，这个散点图是否适合直线拟合？那如果再多几个样本点呢？这样是否适合呢？

师生互相讨论后得出要引入一个统计量来定量的刻画样本数据的线性相关程度.

设计意图：引导学生分析一组数据是否能进行直线拟合不能仅仅通过肉眼观察，而是需要一个统计量来定量刻画线性相关程度的强弱，进而引出本节课的研究目标.让学生初步感受构建一个统计量的必要性，从定性向定量过渡，从而自然引出相关系数.

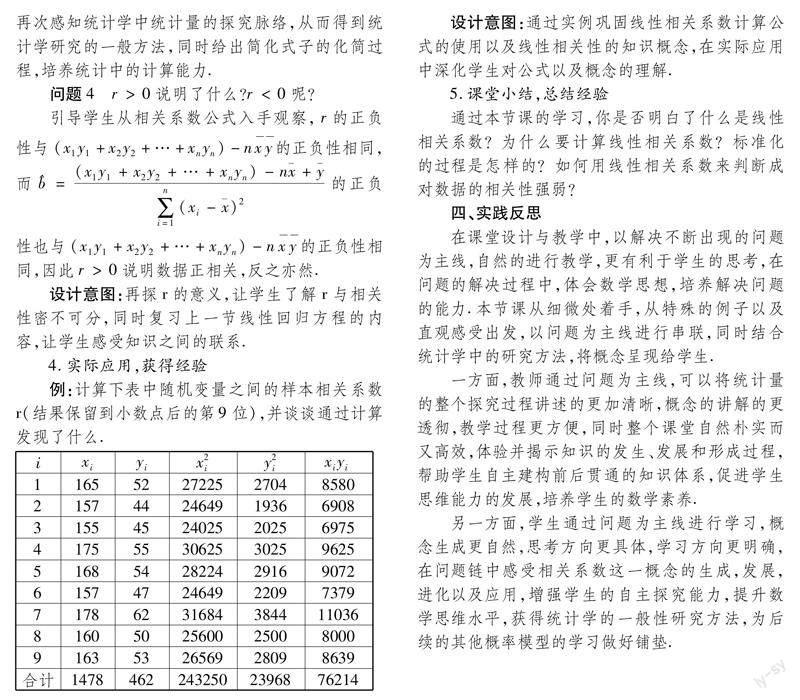
设计意图：通过实例巩固线性相关系数计算公式的使用以及线性相关性的知识概念，在实际应用中深化学生对公式以及概念的理解.

5.课堂小结，总结经验

通过本节课的学习，你是否明白了什么是线性相关系数？为什么要计算线性相关系数？标准化的过程是怎样的？如何用线性相关系数来判断成对数据的相关性强弱？

四、实践反思

在课堂设计与教学中，以解决不断出现的问题为主线，自然的进行教学，更有利于学生的思考，在问题的解决过程中，体会数学思想，培养解决问题的能力.本节课从细微处着手，从特殊的例子以及直观感受出发，以问题为主线进行串联，同时结合统计学中的研究方法，将概念呈现给学生.

一方面，教师通过问题为主线，可以将统计量的整个探究过程讲述的更加清晰，概念的讲解的更透彻，教学过程更方便，同时整个课堂自然朴实而又高效，体验并揭示知识的发生、发展和形成过程，帮助学生自主建构前后贯通的知识体系，促进学生思维能力的发展，培养学生的数学素养.

另一方面，学生通过问题为主线进行学习，概念生成更自然，思考方向更具体，学习方向更明确，在问题链中感受相关系数这一概念的生成，发展，进化以及应用，增强学生的自主探究能力，提升数学思维水平，获得统计学的一般性研究方法，为后续的其他概率模型的学习做好铺垫.

本文系江西省教育科学 “十四五”规划2022年度课题《高中数学“一课四研”教研范式的研究》（编号：22PTZD035）的研究成果.