数学通讯第531号问题的另解

陆信明　周娜

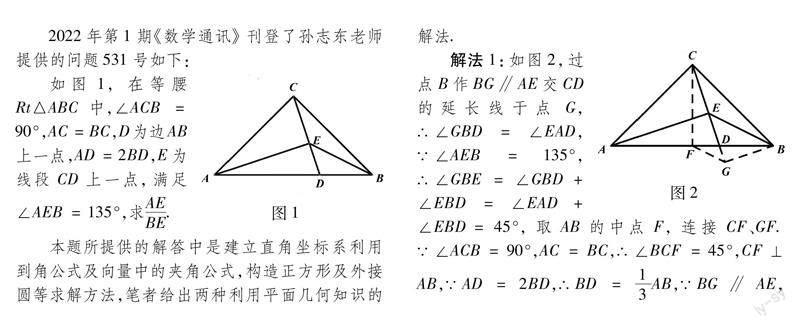
2022年第1期《数学通讯》刊登了孙志东老师提供的问题531號如下：

如图1，在等腰Rt△ABC中，∠ACB=90°，AC=BC，D为边AB上一点，AD=2BD，E为线段CD上一点，满足∠AEB=135°，求AE/BE．

本题所提供的解答中是建立直角坐标系利用到角公式及向量中的夹角公式，构造正方形及外接圆等求解方法，笔者给出两种利用平面几何知识的解法．

由上述二解可见，本题解答的难点在于∠AEB=135°这一条件的运用，通过观测不难猜得∠AED=90°，∠BED=45°，这为解决问题提供了方向．解法1从AD=2BD入手，构造相似三角形，通过将已知中135°角转移，构造B、G、F、C四点共圆，得出∠AED=90°，从而解决了问题．解法2也是从AD=2BD入手，构造相似三角形、等腰直角三角形，由全等三角形，得出∠BEF=45°，最终也实现问题的解决．

参考文献

［1］陆信明．数学通报2596号问题的另证与推广［J］．中学数学教学，2021（1）：57．