基于加权马尔科夫-ARIMA修正模型的区域物流需求预测

程元栋,喻可欣,李先洋

安徽理工大学经济与管理学院,安徽 淮南 232001

0 引言

精准的物流需求预测能为政府、交通运输行业在物流规划、物流基础设施投资与建设、产业规划与布局等方面提供有力的决策依据,同时可帮助相关企业及经营者调节日常物流生产活动,指导作出最优决策。物流需求作为派生性需求,不仅与区域经济发展相关,还受多方面因素制约,难以从单一维度进行分析[1]。

目前物流需求预测研究多基于物流量的历史数据,采用单一或组合模型进行预测[2]。刘炯[3]、王迪[4]基于多项历史数据,采用多元线性回归模型对物流需求及其影响因素进行实证分析;吴玉国等[5]采用灰色-马尔科夫组合模型建立货运周转量预测体系;武亚鹏等[6]运用有效度法对线性回归模型、自回归移动平均(autoregressive integrated moving average,ARIMA)模型进行线性组合,预测武汉市的物流需求;张婉琳[7]将灰色关联预测与ARIMA模型预测组合,预测宁波港口物流需求。

ARIMA模型是计量经济学中的一类模型,能有效拟合预测对象的时间序列,但采用单一ARIMA模型预测时,可能会在部分时刻因外部因素冲击,导致预测数据与实际数据存在较大偏差,具体表现为残差的异方差性[8]。本文采用加权马尔科夫模型修正残差序列,构建加权马尔科夫-ARIMA修正模型,以国家统计局公布的我国1991年1月至2021年12月的货运周转量为物流需求数据进行实例分析,验证加权马尔科夫-ARIMA修正模型对区域物流需求预测的准确性,以期为物流规划决策活动提供前提依据。

1 模型构建

1.1 ARIMA模型

将自回归(auto regressive,AR)模型、移动平均(moving average,MA)模型和差分法结合构成ARIMA模型,采用ARIMA模型可将一组单变量的时间序列,采用差分等方式把不可预测的非平稳序列转化为平稳序列,通过构建数学模型进行统计描述[9]。假设自回归阶数为p,原始数据差分后达到平稳的次数为d,移动平均阶数为q,则ARIMA(p,d,q)模型为:

式中:▽dyt为序列yt的d阶差分,αi为第i项的自回归系数,βj为第j项的移动平均系数,εt为yt的残差。

1.2 加权马尔科夫模型

加权马尔科夫模型以残差序列的各阶自相关系数体现不同滞期各状态间相互影响的强弱,能有效利用历史数据[10]。实际货运周转量序列减去ARIMA模型预测的货运周转量序列,得到随机残差序列,将残差序列划分成多种状态,计算一步转移频数矩阵与一步转移概率矩阵,进行马氏性检验[11]。通过马氏性检验后,采用残差序列的各阶自相关系数确定各阶权重,加权求和后预测将来期数的状态。最后依据模糊集理论中的状态特征值,将预测状态转变为预测结果,实现修正残差序列的目的[12]。

构造χ2统计量,对残差序列进行马氏性检验,公式为:

(1)

式中:fij为状态i一步转移至状态j的频数,pij为转移概率,p·j为边际概率,m为矩阵的行(列)数。

根据分级情况,计算对应阶数的自相关系数,k阶的自相关系数

(2)

将rk归一化,得到k阶权重

(3)

状态i的加权和

(4)

式中pi为k阶滞期时状态i的转移概率。

依据最大概率隶属度原则,max{Pi}对应状态为该期残差的预测状态。

采用模糊集理论中的状态特征值,将预测状态转化为预测结果,公式为:

(5)

(6)

式中:di为本期预测的max{Pi}状态权重;ξ为最大概率作用指数,一般ξ=2或ξ=4,本文取ξ=2;H为max{Pi}时状态i对应的级别特征值。

预测残差

(7)

式中Ti、Bi分别为预测状态i对应的区间上限、区间下限。

1.3 加权马尔科夫-ARIMA修正模型

通过加权马尔科夫模型预测残差,修正ARIMA模型预测的第t期货运周转量

(8)

2 实例分析

2.1 ARIMA模型预测

2.1.1 数据选取

货运量与货运周转量反映某地区在一定时间内的物流活动情况,货运量是一定时期内运输的实际货物总量,货运周转量包括货物数量和货物要求运输的距离,更能体现对物流运输的需求[13-15]。选取国家统计局公布的我国1990年1月至2021年12月的货运周转量数据进行分析,共计384期,每月为1期。货运周转量时序图如图1所示[16]。由图1可知:第145期(2002年)前货运周转量平稳增长,之后出现大幅增长;每年2月的货运周转量均下降明显。我国的货运周转量呈非平稳的周期性增长。对货运周转量进行差分处理,经1阶差分及平稳性检验发现,序列的增长趋势消失,显示一定的平稳性。

图1 货运周转量时序图

2.1.2 模型识别

为确定模型阶数[17],在统计应用软件R中绘制原货运周转量序列的自相关系数图和偏自相关系数图,如图2所示。

a)自相关系数 b)偏自相关系数 图2 原货运周转量序列的自相关系数图和偏自相关系数

由图2可知:1阶差分后自相关系数与偏自相关系数均拖尾,采用ARIMA(p,q)模型。根据最小信息准则,采用赤池信息准则(Akaike information criterion,AIC)和贝叶斯信息准则(Bayesian information criterion,BIC)确定p、q,均支持原货运周转量序列的ARIMA(2,1,2)模型,即1阶差分序列的ARIMA(2,2)模型最优。

2.1.3 ARIMA模型预测结果

确定模型阶数后,估计ARIMA模型的系数,拟合结果为:AR(1)、AR(2)、MA(1)、MA(2)的系数分别为1.489 3、-0.555 9、-1.909 8、0.937 7;标准差分别为0.174 0、0.049 5、0.034 5、0.029 9。ARIMA模型系数的绝对值大于3倍标准差,系数均显著。因此可得ARIMA(2,1,2)模型为:

yt=2.489 3yt-1-2.045 2yt-2+0.555 9yt-3+εt-1.909 8εt-1+0.937 7εt-2。

根据拟合的模型,可得ARIMA模型预测货运周转量序列。

2.2 加权马尔科夫模型残差修正

ARIMA模型预测的货运周转量序列与实际货运周转量序列之差构成残差序列,该序列可看作一组具有平稳性与无后效性的随机变量[18-20]。采用加权马尔科夫模型修正残差序列,将修正后的残差序列与ARIMA模型预测的货运周转量序列相加,计算修正预测货运周转量。

2.2.1 状态分级

经计算残差序列的均值为-41.6,标准差为456.3,依据均值-标准差法,将残差序列分为7个状态区间,如表1所示。

表1 残差序列的状态区间划分

2.2.2 计算转移概率矩阵

根据残差序列的转移情况进行统计,得到一步转移频数矩阵p,计算一步转移概率矩阵p(1),结果为:

p·j为p的第j列之和除以各行各列总和,经计算边际概率p·1=0.257 2,p·2=0.057 4、p·3=0.235 0、p·4=0.305 0、p·5=0.149 0、p·6=0.078 0、p·7=0.068 0、p·8=0.050 0。参照一步转移概率矩阵,同理可计算出二至七步转移概率矩阵p(2)～p(7)。

2.2.3 马氏性检验

2.2.4 预测残差

根据式(2)(3)计算残差序列的各阶自相关系数及归一化后的各阶权重,结果如表2所示。

表2 各阶自相关系数及权重

将归一化后的各阶权重作为对应滞期的权重,以第1～372期的残差数据为样本数据预测第373～384期的残差。例如预测373期残差状态如表3所示。根据式(4),结合表3数据计算可得状态1～7的Pi分别为0.015 4、0.032 9、0.008 8、0.188 8、0.216 1、0.406 9、0.131 1,max{Pi}=0.406 9,依据最大概率隶属度原则判定,第373期的残差状态为6,分布在区间[415,877)。

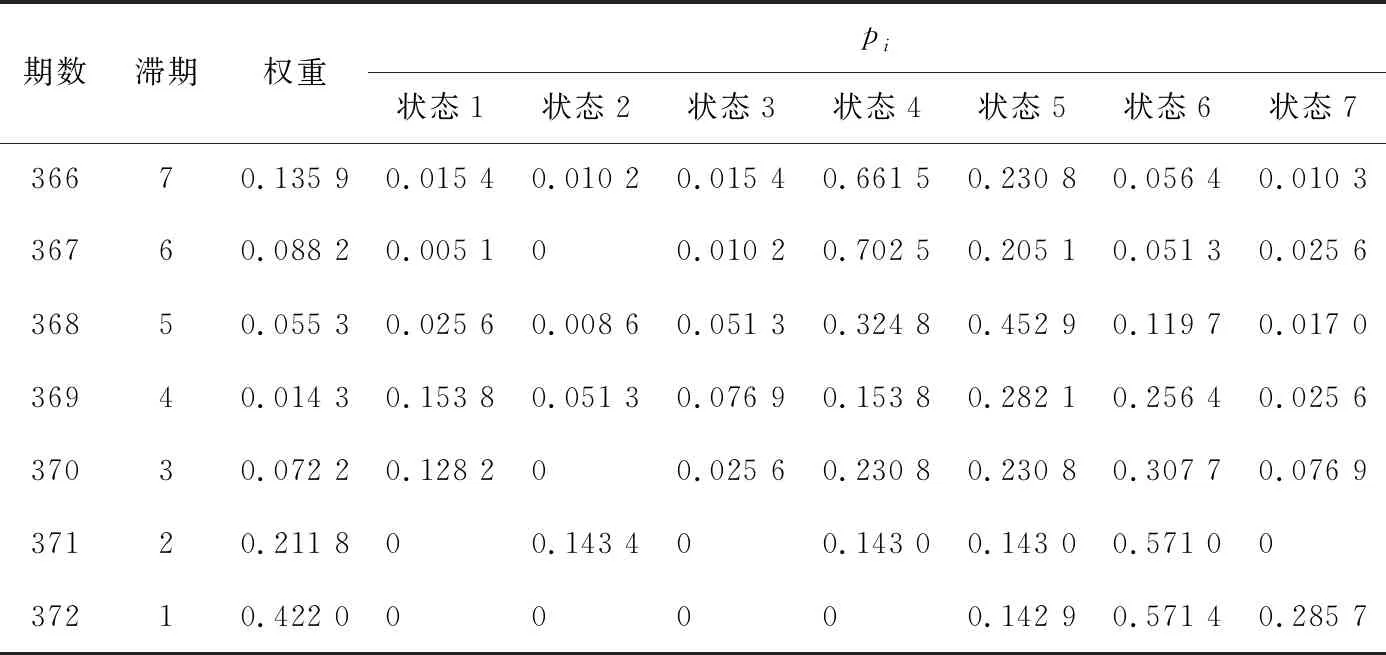
表3 预测第373期残差状态

通过式(5)计算状态1～7的di,结果为:d1=0.008 9,d2=0.004 1,d3=0.008 8,d4=0.133 7,d5=0.175 2,d6=0.621 4,d7=0.064 5。基于模糊集理论中的状态特征值,采用式(6)计算状态特征值H=5.600 31,依据式(7),得第373期的预测残差z=422.569 亿t·km。

2.3 加权马尔科夫-ARIMA修正模型预测

ARIMA模型捕捉的是数据间的线性关系,只需内生变量,使用简单,但对外界的影响,如政策调控或突发事件造成的剧烈冲击很难预测。货运周转量具有明显的周期增长性,且易受外界影响,可采用加权马尔科夫模型预测的残差体现这种非线性变化。根据加权马尔科夫模型预测的第373期残差,采用式(8)将该残差与ARIMA模型预测的货运周转量相加,得到加权马尔科夫-ARIMA修正模型预测的第373期的货运周转量,为17 186.72 亿t·km。依次计算第374～384期的残差及修正预测货运周转量,实际货运周转量Fp与ARIMA模型、加权马尔科夫-ARIMA修正模型预测的货运周转量Ff对比结果如表4所示。

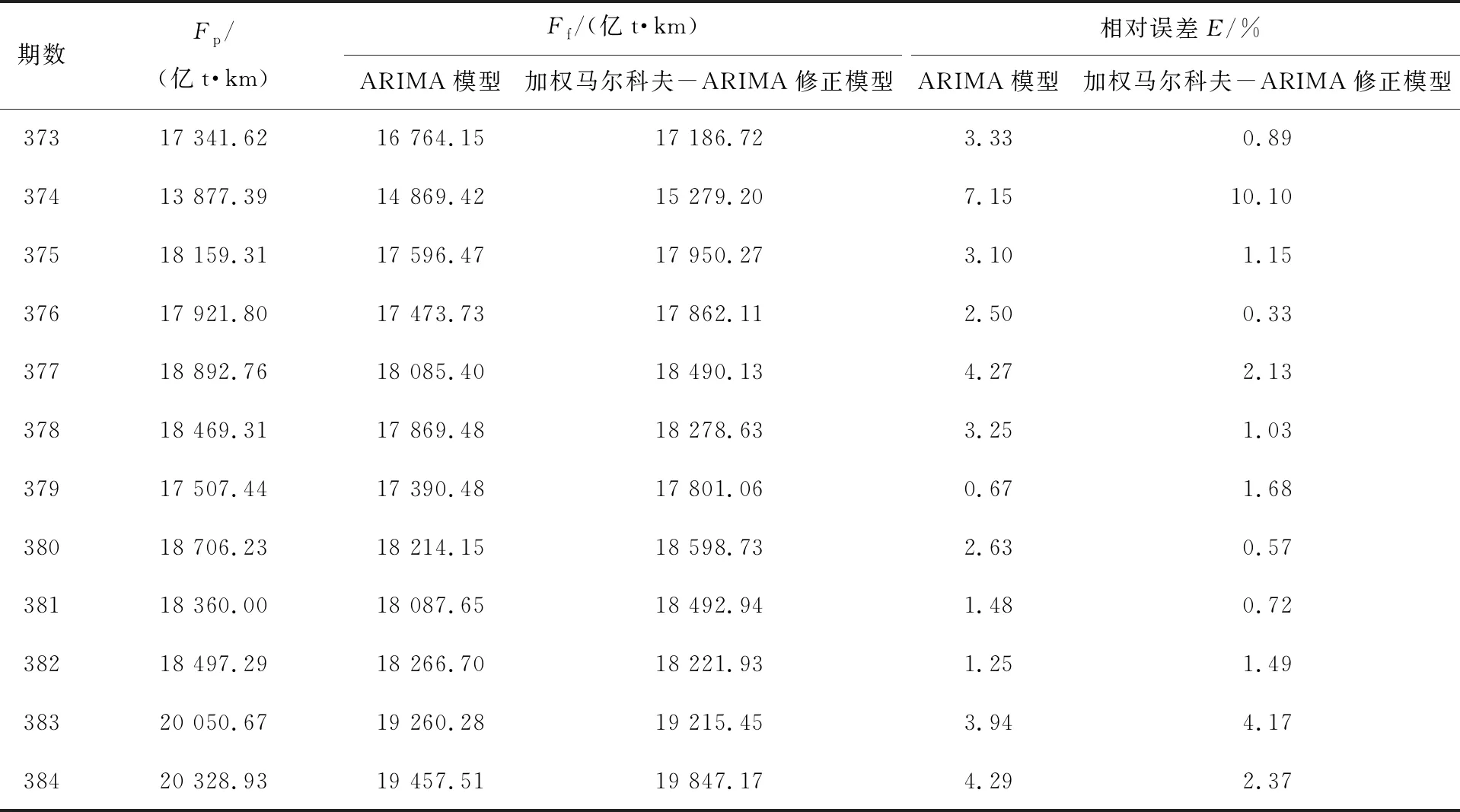
表4 第373～384期的实际货运周转量与2种模型预测的货运周转量

ARIMA模型与加权马尔科夫-ARIMA修正模型的平均相对误差分别为3.15%、2.22%,经修正后提高了模型的预测精度,加权马尔科夫-ARIMA修正模型的预测精度优于单一的ARIMA模型。

3 结论

本文以我国1990年1月至2021年12月的月度货运周转量为预测物流需求的基础数据,构建时间序列的ARIMA模型,采用加权马尔科夫模型修正残差序列,建立加权马尔科夫-ARIMA修正模型,以2021年1月至12月(即文中的373至384期数据)共12期货运周转量为例进行实证分析。结果显示加权马尔科夫-ARIMA修正模型的预测精度优于单一ARIMA模型。加权马尔科夫-ARIMA修正模型可提高区域物流需求预测结果的准确性,为物流决策人员提供可靠的决策依据,也可为其他领域的预测研究提供借鉴。