斜齿轮副齿面修形承载接触动力学分析

刘 星，王会良，2，苏建新，2

（1.河南科技大学机电工程学院，河南洛阳 471003；2.机械装备先进制造河南省协同创新中心，河南洛阳 471003）

1 引言

斜齿圆柱齿轮以其传动平稳、重合度大、啮合性能好等优点，被广泛应用在高速重载的场合中。该材料具有抗冲击以及耐磨等特性被广泛用于风力发电、轮船以及汽车后桥所用齿轮箱中。但设备在高速运转的情况下，齿轮因受较大的载荷，易产生轮齿振动噪声、较大的啮入啮出冲击等问题，会造成齿轮出现各种不同的失效方式从而降低齿轮副的传动精度与寿命［1］。随着高精端设备的不断发展，各机械零部件对齿轮性能的要求越来越高。齿轮在实际传动过程中，由于受安装制造误差、承载变形的影响，常常会出现齿面偏载、胶合、齿根折断等失效方式。而通过对齿面进行微量修整，可以优化齿面接触区域，改善齿轮啮合性能。文献［2］提将3次B样条拟合的修形曲面与小轮理论齿面叠加构造成精确的拓扑修形齿面，建立了小轮拓扑修形面齿轮副TCA、LTCA的计算模型，并用试验验证了理论分析的正确性。文献［3］建立了有限元全齿简化模型，通过二次修正法得到齿廓的精确修形量，并通过修形前后齿面接触应力区域的变化进行对比，说明齿廓修形能够有效改善齿轮啮合性能。文献［4］对内斜齿轮进行三维拓扑修形，建立齿轮副传动误差分析公式，并结合有限元进行算例分析，验证不同修形系数在不同情况下传动误差幅值变化的趋势。

以一对斜齿轮副为研究对象，根据齿轮副基本参数及拓扑修形原理在Mathematica中建立修形与标准斜齿轮的齿面方程，得到不同修形参数的齿面廓形，将齿面以坐标点形式导出，在UG中进行斜齿轮副的三维实体建模与装配。利用有限元的方法对不同修形参数下的齿轮副进行仿真分析。使用ANSYS−Workbench对修形齿轮副的承载能力进行瞬态动力学仿真分析，为后续修形斜齿轮动力学方面的研究提供理论依据。

2 斜齿轮副的三维建模

以斜齿轮齿面啮合原理与加工坐标系转换原理建立斜齿轮数学模型，使用Mathematica软件进行软件编程，求解修形齿轮齿面的三维点坐标。把生成的齿面坐标点集导入三维绘图软件中、通过构建边线、曲面缝合、倒圆角、阵列、旋转拉伸切除生成齿轮的三维实体模型。将Mathematica 生成的修形齿轮齿面点以.DAT的格式保存，并导入到UG中。通过导入点集、延伸片体、曲面缝合、倒圆角等命令生成单个齿面所示，再经由阵列拉伸切除等命令生成修形主动轮三维模型，如图1所示。

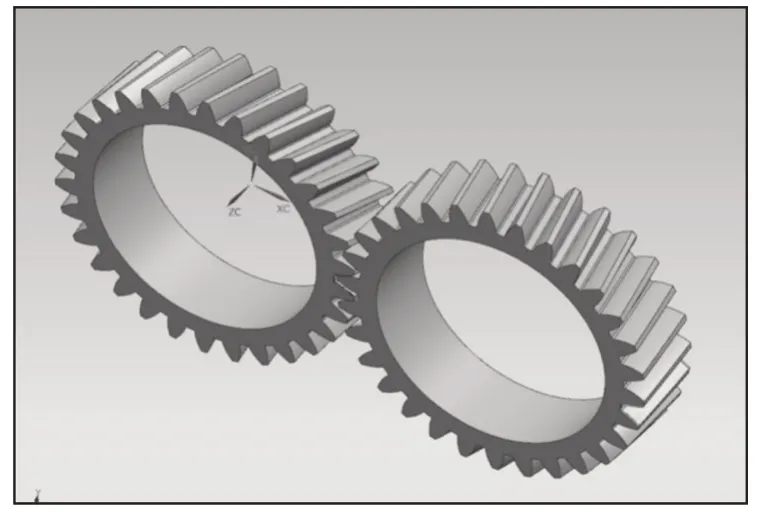
图1 三维模型Fig.1 Digital Model

由图1所示，研究的斜齿轮副是由主动轮和从动轮组合成一对啮合齿对，其基本参数，如表1所示。齿轮副的材料为20CrMn⁃TiH，弹性模量为E= 2.07 × 105MPa，泊松比为0.3，密度为ρ=7.8 × 103kg/m3，抗拉强度为1483MPa，屈服强度为1292MPa，接触许用应力为745MPa，弯曲许用应力为510MPa［11］。

表1 斜齿轮副基本参数Tab.1 Basic Parameters of Helical Gear Pair

3 有限元仿真模型的建立及仿真条件的添加

在UG中建立的斜齿轮副传动系统三维装配模型保存为x.t格式，导入有限元仿真软件ANSYS−Workbench中，建立齿轮副有限元分析模型的五齿啮合模型网格来做齿轮副动力学分析。

如图2所示，在研究斜齿轮副的承载接触特性的有限元仿真分析中，五齿啮合模型的网格节点数为223824，单元数为41280。在斜齿轮副的承载接触特性的有限元仿真模型中，对主动轮旋转轴施加转速20rad/s，从动轮施加500N·m 的阻力矩，且在运行时间内转速和扭矩均为恒定值，计算时间设为0.3s。接触类型选择为摩擦接触，选定摩擦系数为0.1。

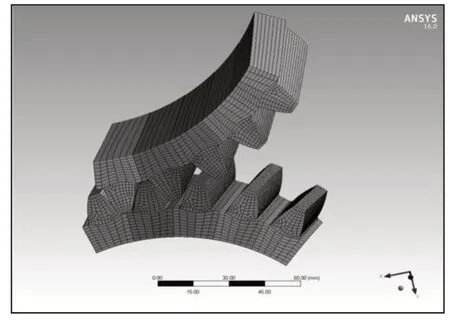
图2 五齿啮合网格分析模型Fig.2 Five−Tooth Mesh Analysis Model

4 修形前的有限元仿真分析

修形前的标准齿轮副在承载条件下的齿面分析，如图3 所示。在计算周期结束时刻齿面受接触应力值是115.6MPa，剪切应力值是81.301MPa，最大等效应力是245.07MPa。在啮合周期内，齿面上整个最大等效应力云图的分布范围表明，未修形的齿轮副其接触印痕为一条倾斜分布整个齿面的直线，应力值分布在整个齿面上，存在齿顶接触与边缘接触。

图3 未修形齿轮副分析结果Fig.3 Analysis Result of Unmodified Gear Pair

5 对齿轮副修形优化

齿轮的传动误差与接触印痕能够体现齿轮副的啮合性能，为考察不同的齿廓和齿向修形参数对齿面承载特性的影响，设置主动轮的四种修形系数，如表2所示。分别对齿轮副进行有限元分析及有限元瞬态动力学分析，通过仿真分析对比不同修形参数下的齿面接触应力值与齿面最大等效应力云图。

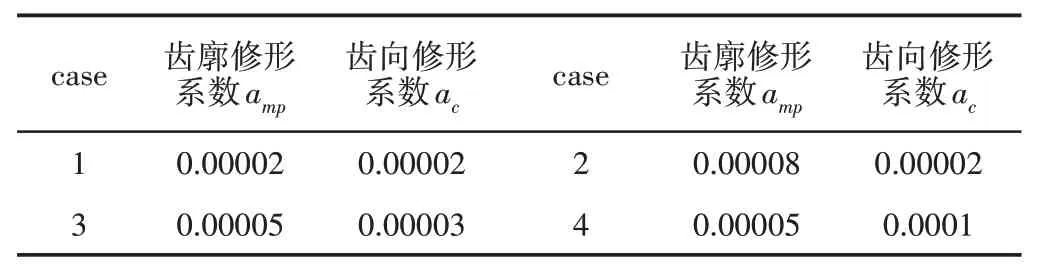
表2 主动轮修形基本系数Tab.2 Basic Coefficient of Driving Wheel Modification

最大等效应力云图，如图4 所示。case1 中修形系数较小，齿面出现较大的啮合干涉现象，最大应力集中在齿顶处，且最大等效应力值为513.33MPa；case2 的最大等效应力值最小为192.14MPa，基本消除了啮合干涉现象，应力最大发生在齿面中部，证明该修形方案下齿面接触特性较好，啮合干涉量较小，能够有效减少齿轮齿顶干涉问题。对比case3 和case4，当齿向修形量增加时，齿轮啮合区域逐渐集中在齿面中部，接触印痕越来越居中。当齿向修形系数过大时，会导致齿面受力急剧扩大，瞬时的接触区域变小。在求解结果里增加一个Contact Tool于从动轮第二齿面为定义接触齿面，来观察在齿轮啮合周期内接触应力的变化趋势，以求解不同修形系数下齿面接触应力幅值变化范围，如图5 所示。从图中可以看出，在啮合周期内，接触应力曲线整体呈开口向下的抛物线形，从case1 到case4 的齿面最大接触应力值分别为262.11MPa、302.79MPa、315.96MPa与404.53MPa。在case1 齿廓修形系数amp=0.00002，齿向修形系数ac=0.00002时，斜齿轮副的接触应力曲线开口较大，坡度较小，说明齿面啮合重合度较大，但有微小的二次应力峰值出现，可能由于齿廓修形量过小，没有完全消除齿顶啮合干涉。从case2 到case4 接触应力曲线坡度逐渐增大，接触应力幅值随着修形系数的增大急剧增大，证明齿面的重合度变小，但随着齿廓修形系数的增加，啮合周期内不再出现二次峰值现象。说明齿廓修形量加大能够有效减少齿轮齿顶干涉问题，可降低齿顶承受载荷，消除齿顶应力集中，使载荷集中于齿的中间区域，改善啮合状况。

图4 最大等效应力云图Fig.4 Maximum Equivalent Stress Cloud Diagram

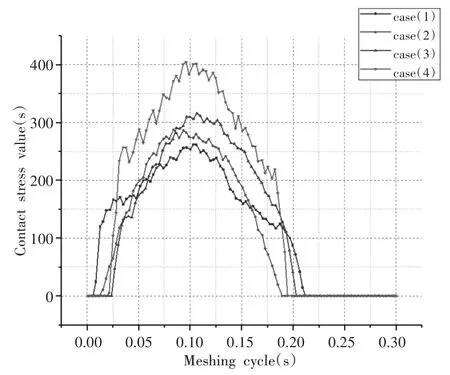
图5 齿面接触应力值Fig.5 Tooth Surface Contact Stress Value

为了更好的了解不同工况下齿轮副传动误差变化情况，在不同修形案例下齿轮副分别设置500N·m、1000N·m以及2000N·m三种扭矩。保持转速20rad/s不变。四种修形系数案例下齿轮副在轻、中、重三种承载情况下传动误差变化情况，如图6所示。

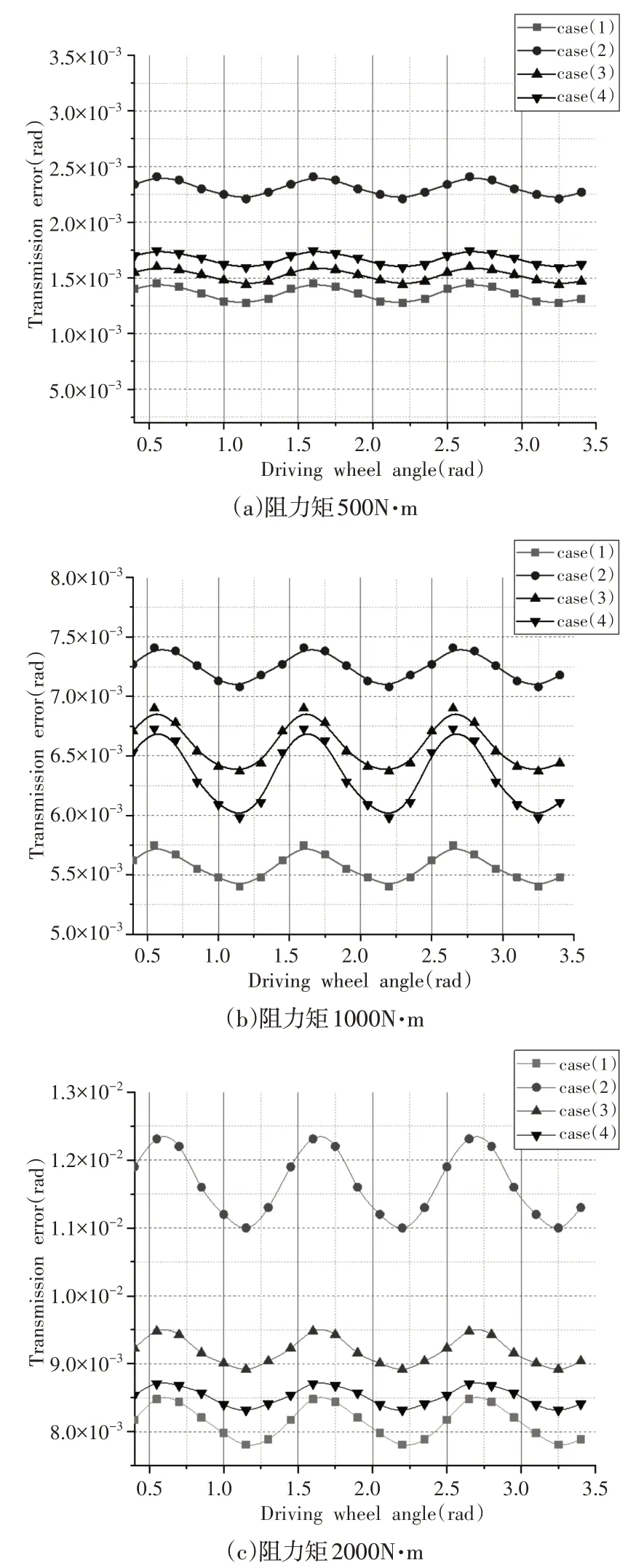
图6 传动误差仿真结果Fig.6 Simulation Results of Transmission Error

从图中可以看出传动误差随着阻力矩增大而增大，且传动误差曲线大致呈正弦曲线波动。当载荷为1000N·m 时，修形系数是amp=0.00005 和ac=0.00003 时，传动误差均值为6.59×10−3rad；修形系数是amp=0.00005 和ac=0.0001 时，传动误差均值为6.34×10−3rad。当载荷为2000N·m 时，修形系数是amp=0.00005 和ac=0.00003 时，传动误差均值为9.18×10−3rad；修形系数是amp=0.00005 和ac=0.0001 时，传动误差均值为8.52×10−3rad。可以看出，case3的传动误差均大于case4。当修形系数是amp=0.00002和ac=0.00002 时，在三种载荷下传动误差均为最小，分别为1.45×10−3rad、5.56×10−3rad、8.14×10−3rad；当修形系数是amp=0.00008和ac=0.00002 时，传动误差均为最大，分别为2.31×10−3rad、7.24×10−3rad、11.64×10−3rad。可以看出，载荷相同的情况下，齿廓修形系数的增加对传动误差幅值影响较大。不同阻力矩下传动误差幅值，如图7 所示。当载荷为500N·m，修形系数是amp=0.00002和ac=0.00002 时，传动误差幅值最小，为1.45×10−3rad；当1000N·m 时，修形系数是amp=0.00002 和ac=0.00002 时，传动误差幅值最小，为5.75×10−3rad；当2000N·m 时，修形系数是amp=0.00002 和ac=0.00002 时，传动误差幅值最小，为8.48×10−3rad。其中在三种阻力矩下，case1 的误差幅值最小，变化趋势较为稳定；而case2传动误差幅值最大。可以看出在不同阻力矩下，修形系数不同，其传动误差幅值变化形式不同。齿轮副受轻载时，修形系数对传动误差幅值影响较小；但随着载荷增大，幅值变化呈增大趋势。承载时齿轮副传动误差的幅值能反映出传动过程中的振动情况，幅值越大，振动就大，发出的噪声也会变大。因此，需要根据不同工况来合理选择修形系数，减少斜齿轮副的传动误差影响，才能得到理想的啮合传动特性。

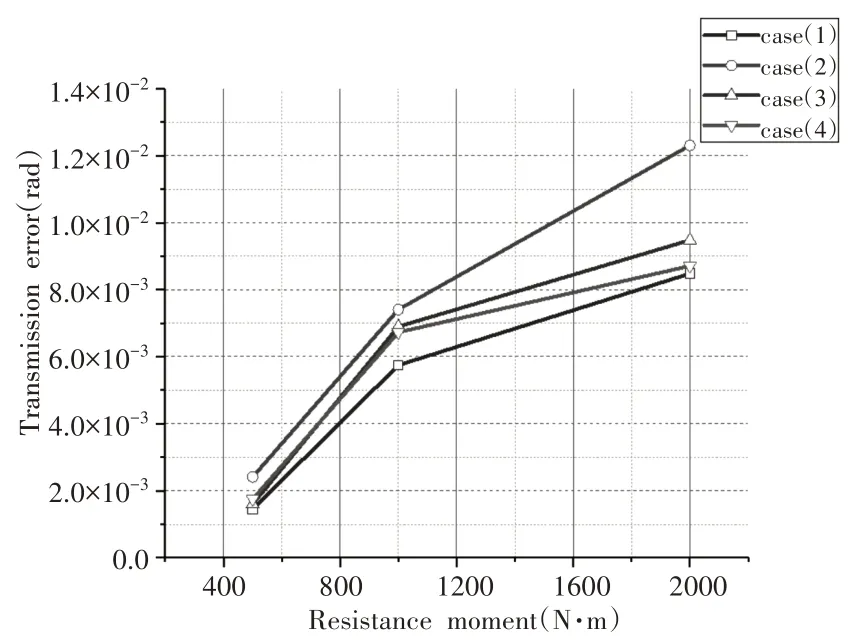
图7 不同阻力矩下传动误差幅值Fig.7 Transmission Error Amplitude Under Different Resistance Torques

6 结论

以一对斜齿轮副为研究对象，在Mathematica中进行修形齿面建模，运用Workbench修形齿轮副的承载能力进行仿真分析，对比未修形的标准齿轮副在承载条件下的齿面分析结果，改变不同的齿廓、齿向修形系数，求解出不同修形系数下齿轮副的传动误差与接触印痕，得出不同修形系数下齿面接触应力与最大等效应力云图，分析修形参数对齿面接触特性的影响，并设置多种载荷来考察齿轮副传动误差的幅值。结果表明，齿廓修形对传动误差幅值影响较大，齿向修形对齿面接触区域影响较大。在不同载荷下，不同的修形系数对齿轮副的传动特性影响不同，其传动误差幅值变化趋势也不同。要结合实际工况来选择合适的修形系数，才能得到所需的齿轮啮合性能，这为后续修形斜齿轮动力学方面的研究提供理论依据。