二自由度六杆机构轨迹综合的代数求解

李学刚，张丽娟，冯立艳，张 英

（1.华北理工大学机械工程学院，河北唐山 063210；2.北京邮电大学自动化学院，北京100876）

1 引言

随着机电智能化、运动可控化、机电一体化的发展，实现可控、可调运动输出成为现代机构系统的新要求，二自由度六杆机构作为混合驱动可控机构的运动合成机构，是在原五杆机构的基础上引入调节杆，增大了机构的柔性和可调可控性，在微型结构、高精度等工程领域应用越来越广泛。

当各原动件按定传动比运动时，该机构仍为二自由度机构，与五杆机构［1−2］和类四杆五杆机构［3］相比，其尺寸类型和输入运动变化大，输出轨迹更为丰富多样，运动特性易于调整，在实现混合驱动运动合成时，可有效减小伺服电机的运动补偿量，使机构获得良好的动力学性能［4］。

目前文献中对该机构进行轨迹综合的方法主要有优化法［4−8］、图谱法［9−10］等。图谱法适用范围广，求解速度快，计算复杂程度低，但存在完备数值图谱库建立难度大，求解精度低的不足。优化法可以求解得到精度较高的综合结果，且可实现多点位的连续轨迹综合，但该方法受初值选取、目标函数性态和寻优方法的影响，有时难以得到全局最优结果。

针对二自由度六杆机构提出了一种基于傅氏级数的轨迹综合的代数求解新方法，与原有方法相比，该方法解的精度高，完备性强，且克服了原有代数法难以实现多点位连续轨迹综合的不足，能够同时得到多组满足要求的机构尺寸型。有效扩大了代数法的适用范围，提高了连杆机构近似运动综合的求解精度和速度。

2 连杆曲线的傅氏级数表示

二自由度六杆机构示意图，如图1所示。机构各杆的尺寸分别为a、a′、b、c、d。其中AA′、A′B、DE为原动件，BC、CD为连杆。原动件的初始相位角分别为q1、q2、q3，ω1、ω2、ω5分别为曲柄的转速，且有ω1=hω、ω2=kω、ω5=uω（h，k，u为整数）。固定铰链点A、E到原点o的距离分别为r1、r2，旋转角度分别为μ1、μ2，C点为连杆轨迹生成点。

图1 二自由度六杆机构示意图Fig.1 An Illustration of 2−DOF Hinge Six−Bar Mechanism

由文献［11］可知，当输入构件以匀速转动时，角度φ1、φ2、φ3均为以时间t为变量的周期性函数，C点产生的连杆曲线为周期性封闭曲线，可以表示为以时间t为变量的傅氏级数之和：

式中：i=；cn—轨迹生成曲线rC傅氏级数展开的谐波参数。

且有：

二自由度六杆机构的连杆曲线可以用一系列的离散点表示，因此，cn通常可以用数值方法计算得到。根据离散傅里叶变换的性质［11］，谐波参数cn数值解的计算表达式为：

3 综合设计方程建立

由图1所示，二自由度六杆机构的轨迹综合，需要确定12个独立设计变量：a、a′、b、c、d、q1、q2、q3、r1、μ1、r2、μ2，为使所建立的综合设计方程能够求解方便，将该机构拆分两部分求解机构的设计参数。针对二自由度六杆机构的轨迹综合问题，已知条件为目标轨迹或轨迹方程，所求为能实现给定目标轨迹方程的机构各杆长尺寸、初始相位角、机构位置参数。由文献［4］可知，二自由度六杆机构的连杆曲线将在原齿轮五杆机构的基础上内凹或外凸，机构A′B与A′A的传动比为i=ω1/ω2= 2时，求解二自由度六杆机构的设计参数。

3.1 左侧三杆组的求解

如图1 所示，应用矢量分析法，建立含有未知设计参数r1、μ1、a、a′、b、q1、q2的左侧三杆组封闭矢量方程：

式（4）的复数矢量形式为：

取式（5−1）的共轭可得：

将h= 2，k= 1 带入式（5−1）和式（5−2），并将两式相乘化简可得：

其中，

由文献［11］可知，利用傅氏级数表示曲线谐波参数时，取有限项低次谐波就可较好的表示原函数，这里取n=−3，−2，…，2，3。由式（1）可知，rC可以表示为以时间t为变量的傅氏级数之和：

将展开后的rC带入式（6）化简可得：

其中，

其中：

分析式（8）发现，表达式H0，H1，H−1，H2，H−2，H3，H−3为完整系数表达式，即当rC、rˉC取更高次谐波时，其将不再变化［13］，由复指数的性质可知，这些表达式的值应为0，由此可以得到如下方程：

方程（9）即求解左侧三杆组设计变量的综合方程，h−1、h1、h2、h−2、h3、h−3、h0为含有设计参数的未知变量，cn(n=−3，−2，…，2，3)可由离散傅里叶变换计算得到。以为变量，计算式（9−1）～式（9−6）求解方程组。将所得到的h−1、h1、h2、h−2、h3、h−3的解带入方程（9−7）可求得变量h0的解。求得到h−1、h1、h2、h−2、h3、h−3、h0解后，可由下列公式得到的解。

3.2 右侧二杆组求解

在得到左侧三杆组设计参数r1、μ1、a、a′、b、q1、q2的基础上，如图1 所示。应用矢量分析法，建立含有右侧未知设计参数r2、μ2、d、c、q3的封闭矢量方程：

方程（10）的复数矢量形式为：

取式（11−1）的共轭可得：

将u= 1 带入式（11−1）和式（11−2），并将两式相乘，化简可得：

其中，

利用傅氏级数表示曲线谐波参数时，取有限项低次谐波就可较好的表示原函数［11］，这里取n=−3，−2，…，2，3。将展开后的rC、rC带入式（12）化简可得：

其中，

其中，

分析式（13）发现，在表达式Hi′(i=−3，−2，…，2，3) 中H0′、H−1′、H1′、H2′、H−2′为完整系数表达式，即当rC取更高次谐波时其将不再变化。由复指数的性质可知，这些表达式的值应为0，由此可以得到如下方程：

方程（14）即求解右侧二杆组设计变量的综合方程，cn(n=−3，−2，…，2，3)可由离散傅里叶变换计算得到。借助Math⁃ematica软件中的GroebnerBasis命令，以h−5、h5、h−4、h4为变量，计算式（14−1）～式（14−4）的Groebner基，得到关于h−5一元四次方程如下：

式中：ki′= 0，1，2，3，4—由目标轨迹谐波参数cn，构成的已知量。

求解方程（15）可得到h−5的4个非零解析解，将所得到的h−5解带入式（14−1）～（14−4）的方程组中，即可求得h5、h−4、h4的解，将所得结果带入方程（14−5）可求得变量h6的解。求得到h−5、h5、h−4、h4、h6解后，可由下列公式得到d、q3、r2、μ2、c的解。

分析方程求解过程可知d、q、3r、2μ、2c的解最终均可转化为仅含有(n=−3，−2，…，2，3)的计算公式，其为二自由度六杆机构右侧二杆组设计参数的计算通式。

将左右两侧设计参数组合，可以得到多个二自由度六杆机构，将综合所得机构带入仿真程序，进行运动分析，检验是否存在曲柄，有无分支、顺序问题，并依据综合误差，最终可得到最优综合结果。

4 综合步骤

依据前面分析，可以建立二自由度六杆机构轨迹综合的代数方法，具体步骤如下：

（1）将二自由度六杆机构拆分两部分，根据目标轨迹生成任务，利用式（4）对目标轨迹进行傅里叶变换，计算得到目标轨迹的谐波参数cn。

（2）将所得到的谐波参数cn代入机构左侧三杆组的方程组中，计算得设计变量h−1、h1、h2、h−2、h3、h−3、h0的解。由设计参数计算公式可求得参数r1、μ1、a、a′、b、q1、q2。

（3）将目标轨迹的谐波参数cn带入右侧二杆组设计参数的计算通用公式，求解得到设计参数r2、μ2、c、d、q3。

（4）对所得多个二自由度六杆机构进行运动分析，检验其是否存在曲柄，有无分支问题、顺序问题，最终得到满足设计要求的二自由度六杆机构。

5 综合实例

（1）根据目标轨迹得到二自由度六杆机构连杆曲线的谐波参数cn，如表1所示。将上述所得谐波参数cn的值带入二自由度六杆机构左侧方程组中计算得到h−1、h1、h2、h−2、h3、h−3、h0的解，由设计参数计算公式可求得r1、μ1、a、a′、q1、b、q2。

表1 目标轨迹点的谐波参数Tab.1 Fourier Coefficients of Coordinates of Prescribed Points

（2）将目标轨迹的谐波参数cn带入右侧二杆组设计参数的计算通用公式，求解得到设计参数r2、μ2、c、d、q3。

（3）将两部分的解过进行组合，应用仿真程序对所得综合结果进行运动分析和检验，得到满足设计要求的机构参数如下：

第一组

r1= 127.8757，μ1= 1.3993，a= 52.1775，a′= 2.1050，q1= 0.0491，q2=−3.0434，b= 80.5811，d= 37.0150，

r2= 53.6080，μ2=−1.6810，c= 209.2492，q3= 0.3203

第二组

r1= 127.8757，μ1= 1.3993，a= 52.1775，a′= 2.1050，

q1= 0.0491，q2=−3.0434，b= 80.5811，d= 37.0450，

r2= 305.340，μ2= 1.5901，c= 209.2492，q3=−0.2221

第三组

r1= 118.9139，μ1= 0.5690，a= 30.1116，a′= 2.0495，

q2= 1.9544，q1= 0.0570，b= 63.9338，d= 52.3545，

r2= 343.9492，μ2= 0.3751，c= 219.8096，q3= 0.0491

第四组

r1= 212.9589，μ1= 1.0811，a= 30.1116，a′= 2.0495，

q1= 0.0411，q2=−1.7581，b= 63.9338，d= 37.0450，

r2= 305.3396，μ2= 1.5901，c= 209.2492，q3=−0.2221第五组

r1= 212.9589，μ1= 1.0811，a= 30.1116，a′= 2.0495，q1= 0.0411，q2=−1.7581，b= 63.9338，d= 52.3545，r2= 343.9492，μ2= 0.3751，c= 219.8096，q3= 0.0491

第六组

r1= 161.3913，μ1= 0.8958，a= 41.1465，a′= 0.6027，

q2=−3.0434，q1= 0.0491，b= 11.3230，d= 52.3545，

r2= 343.9492，μ2= 0.3751，c= 219.8096，q3= 0.0491

第七组

r1= 222.9913，μ1= 0.6005，a= 52.1772，a′= 0.8993，

q1= 0.0490，q2= 0.0982，b= 84.6811，d= 37.0450，

r2= 53.6080，μ2=−1.6810，c= 209.2492，q3= 0.3203

第八组

r1= 222.9913，μ1= 0.6005，a= 52.1772，a′= 0.8993，

q1= 0.0490，q2= 0.0982，b= 84.6811，d= 37.0450，

r2= 305.3396，μ2= 1.5901，c= 209.2492，q3=−0.2221

第九组

r1= 118.914，μ1= 0.5690，a= 30.1116，a′= 2.0495，

q2= 1.9544，q1= 0.0570，b= 63.9338，d= 37.0450，

r2= 53.6080，μ2=−1.6810，c= 209.2492，q3= 0.3203

综合所得机构的运动仿真图，如图2所示。经进一步验证，发现满足杆长条件的9组解，均能较好的生成目标轨迹。目标轨迹与机构生成轨迹的比较图，如图3所示。从图中可以看出，综合所得机构生成的轨迹与目标轨迹十分接近，说明文中建立的二自由度六杆构轨迹综合的代数方法具有较高的综合精度。

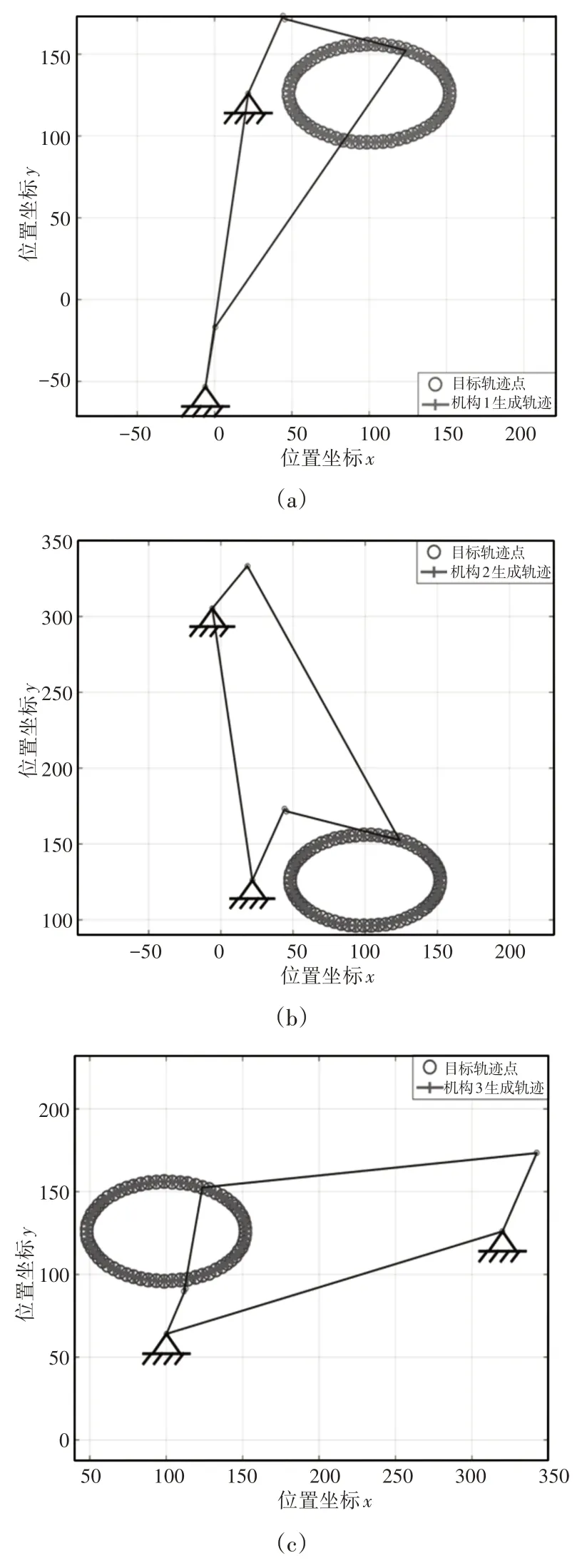
图2 机构运动仿真图Fig.2 Simulation Analysis of Mechanism

图3 综合机构生成轨迹与目标轨迹点图的比较Fig.3 Comparison between Prescribed Points and Corresponding Generated Path

综合所得机构的运动轨迹图，如图3 所示。从图中可以发现，综合所得9个机构均能较好的生成目标轨迹，其中机构7为最优机构。应用优化方法［4］综合所得机构生成轨迹和文中代数法综合所得机构7生成轨迹与目标轨迹的比较图，如图4所示。从图中可以发现，与优化法的综合结果相比较，文中方法综合所得机构的生成轨迹与目标轨迹的拟合情况更好，所得结果更为精确，误差更小。比于优化方法，这里方法不但获得较高精度的综合结果，而且可以同时获得多个在一般安装位置的机构尺寸型，这为设计者优化机构其他性能提供了更多的选择。

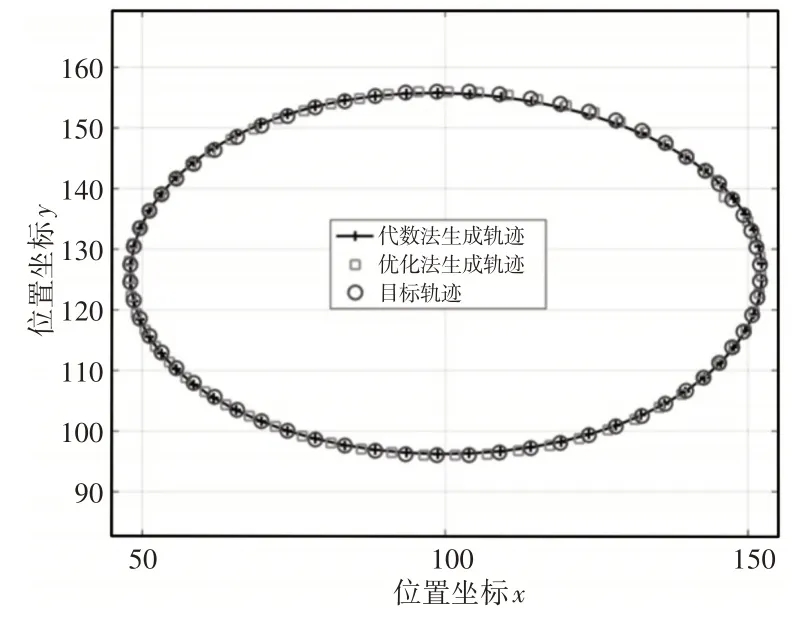
图4 机构生成轨迹与目标轨迹点图的比较Fig.4 Comparison Between Prescribed Points and Corresponding Generated Path

6 结论

建立了一种基于傅氏级数的二自由度六杆机构轨迹综合的代数求解新方法。与已有的综合方法相比，该方法无需给定初值和建立数值图谱库，不需要进行查找和迭代运算，具有计算速度快、求解精度高、可重复性强的优点；二自由度六杆机构相比于齿轮五杆机构得到轨迹类型更加丰富，满足要求解的个数更多，可以为设计者提供更多的选择。如果该方法所得结果的精度不能满足设计要求，可将其作为初值进行优化综合，进一步得到满足设计要求的结果。