后掠翼外挂系统非线性响应分析
肖艳平,王 越,黄 波
(中国民用航空飞行学院,四川广汉 618307)
1 引言
现代飞机在进行颤振分析时,由于计入非线性项的影响,机翼颤振特性呈现复杂的变化,对于后掠翼外挂系统这样的复杂结构,简单的颤振分析是无法满足后掠翼外挂系统颤振特性研究的。因此,对后掠翼外挂系统进行非线性响应分析具有十分重要的工程价值。文献[1−5]建立了机翼/外挂系统的气动弹性力学模型,通过数值模拟研究了几何非线性、结构非线性以及间隙非线性等对大展弦比机翼外挂系统气动弹性和稳定性的影响。结果发现,在非线性项影响下,系统呈现复杂的响应。文献[6−7]以大展弦比柔性机翼为模型,采用牛顿力学法建立了机翼结构动力学模型,通过松耦合法耦合结构非线性气动力和非定常气动力建立了非线性气动弹性模型,通过算例分析研究了结构几何非线性效应影响下,来流迎角和机翼展长对颤振特性的影响。文献[8]定量分析参数不确定性对二元机翼颤振可靠度的影响。文献[9]从不同方面介绍了主动控制技术在机翼气动弹性分析中的应用前景。文献[10−11]建立了非线性二元机翼动力学模型,对比分析理论计算和数值计算结果,研究了超高速飞行条件下,机翼的非线性响应。文献[12]以二元机翼为模型,推导了在突风作用下二元机翼的增广状态空间运动方程,通过仿真分析研究了突风对线性刚度系统和非线性刚度系统响应的影响。文献[13]研究了二元机翼−操纵面立方非线性系统的混沌响应,基于能量原理和活塞理论推导了系统运动微分方程,在研究过程中将操纵面运动孤立为单自由度系统强迫振动问题,利用数值积分法研究了系统的复杂响应问题。文献[14−15]建立了二元机翼模型,推导了气动弹性运动方程,综合Runge−Kutta数值方法与Henon方法研究了控制面间隙非线性对二元机翼气动弹性响应问题。综上所述,目前对机翼外挂系统的非线性响应研究较少,且大多以平直翼为模型,没有对后掠翼外挂系统的非线性响应进行研究,但是现代大型运输机普遍采用后掠机翼。因此,对后掠翼外挂系统的非线性响应研究具有重要价值。这里以后掠机翼为模型,推导了后掠翼外挂系统运动微分方程,通过后掠翼翼尖扭转分叉图、典型速度下的相图以及庞加莱截面图研究了后掠翼外挂系统的非线性响应。
2 力学模型
后掠翼上外挂物悬挂点处的截面图,如图1所示。
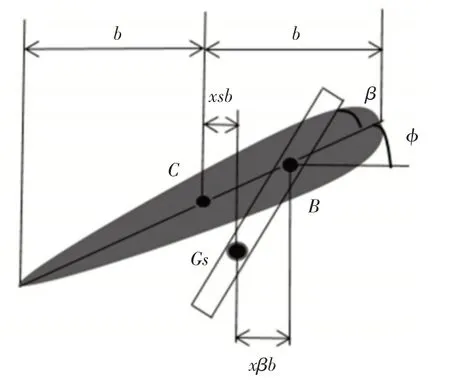
图1 悬挂点处的机翼截面图Fig.1 The Wing Section of Hanging Point
设外挂的质量为ms,用Is表示外挂对于质心的转动惯量,Iβ表示外挂对图中所示的B点的转动惯量,Sβ是外挂物对机翼上B点的质量静矩,xsb为外挂物的质心到机翼弹性轴的距离。后掠翼各参数之间的关系为:
根据文献[13]中平直翼运动方程的推导思路,考虑机翼几何非线性影响,可得后掠翼外挂系统运动微分方程:
式中:Lw—单位展长后掠机翼所受的气动力;
Mθ—气动力对后掠机翼弹性轴的俯仰力矩。
通过修正经典的Theodorsen非定常气动力可建立后掠翼气动力模型,根据文献[16],具体修正方法如下:
得到后掠翼气动力后,代入(1)式可以得到后掠翼系统微分方程。设如下所示无量纲参数:
可以得到:
将上述无量纲参数式(3)代入式(2)和式(3)、式( )2 可得后掠翼外挂系统无量纲方程如下所示:
通过振型函数正交性条件,在式(1)第一式左乘fj,第二式左乘Tj,并将两式在(0~1)之间积分,化简整理后可以得到简化后的系统方程的矩阵形式:
表示状态向量,并满足下列条件:
3 算例分析
根据文献[17],选用的机翼模型参数数据,如表1所示。
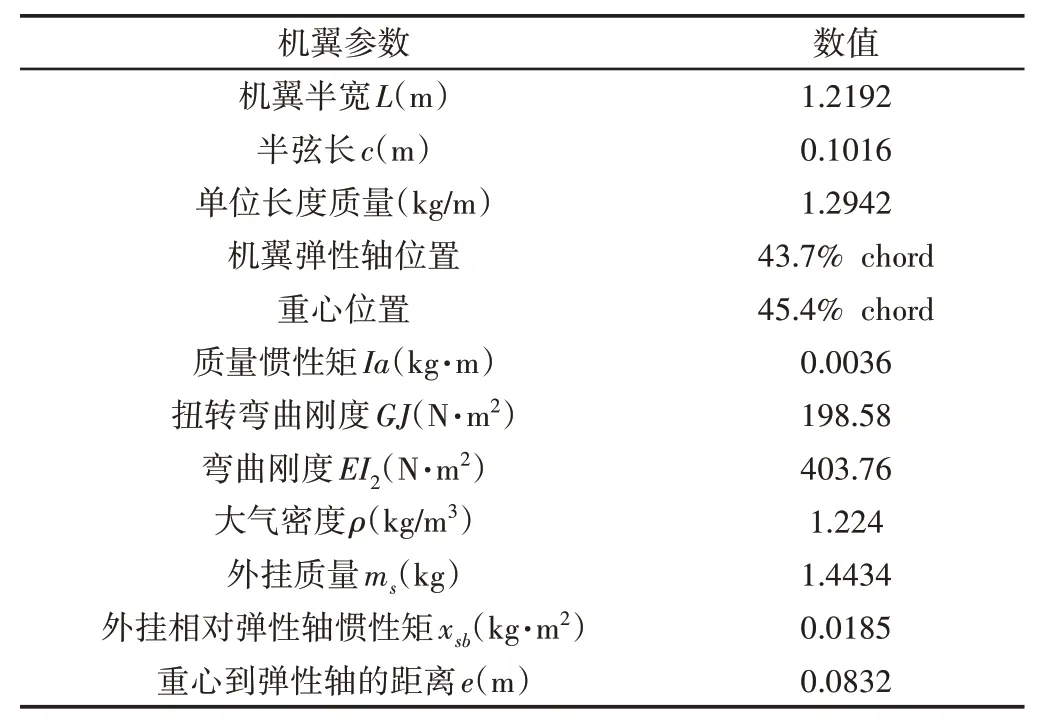
表1 机翼模型参数Tab.1 The Wing Model Parameters
通过不同速度范围内的后掠翼翼尖扭转分叉图,并结合典型速度下的相图和庞加莱截面图,可以判断随着速度增加,后掠翼外挂系统运动状态的变化,从而研究后掠翼外挂系统的非线性响应。将上述模型数据代入方程,取EI2= 199EI1,设外挂模型的参数为:Kβ= 108,μ1= 0.5,xs= 1,ys= 0.3。通过V−g法计算得知,该模型颤振临界速度为96.6m/s。取速度范围为(96~112.2)m/s,后掠翼翼尖扭转角分叉图,如图2所示。从图中可以看出当速度大于颤振临界速度96.6m/s时,系统从收敛的运动状态进入单个极限环运动状态。速度为112m/s时后掠翼外挂系统的相图和庞加莱截面图,如图3、图4所示。由图3、图4可知在该速度下后掠翼外挂系统在相图上所示为一个闭合的圆环,而在庞加莱截面图上该运动状态表现为一个点。当速度范围在(112.2~125)m/s时,后掠机翼系统的翼尖扭转角分叉图,如图5所示。由图5可知当速度大于120.8m/s时,系统由单个极限环运动状态进入周期性双极限环运动状态。速度为125m/s时后掠翼外挂系统翼尖扭转角的相图和庞加莱截面图,如图6、图7所示。从分叉图可知在该速度下系统正在做周期性双极限环运动,在相图中应该出现两个环。但如图6所示,此时的相图并不是两个闭合的环,因此需要借助庞加莱截面图来判断后掠翼系统的运动状态。如图7所示,速度为125m/s时后掠翼系统翼尖扭转角的运动状态在庞加莱截面图上表现为两个点。结合庞加莱截面图、机翼翼尖扭转角分叉图和相图综合判断,可得后掠翼外挂系统此时在做周期性的双极限环运动。
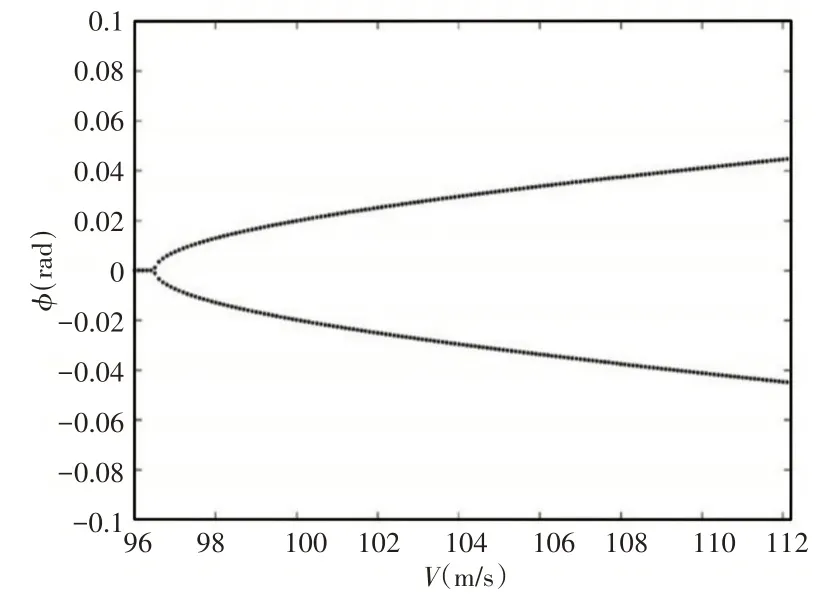
图2 后掠翼外挂系统在(96~112.1)m/s翼尖扭转角分叉图Fig.2 Swept−Back of the Wing with External System in the 96m/s to 112.1m/s Wing Tip Torsional Angle Bifurcation Diagram
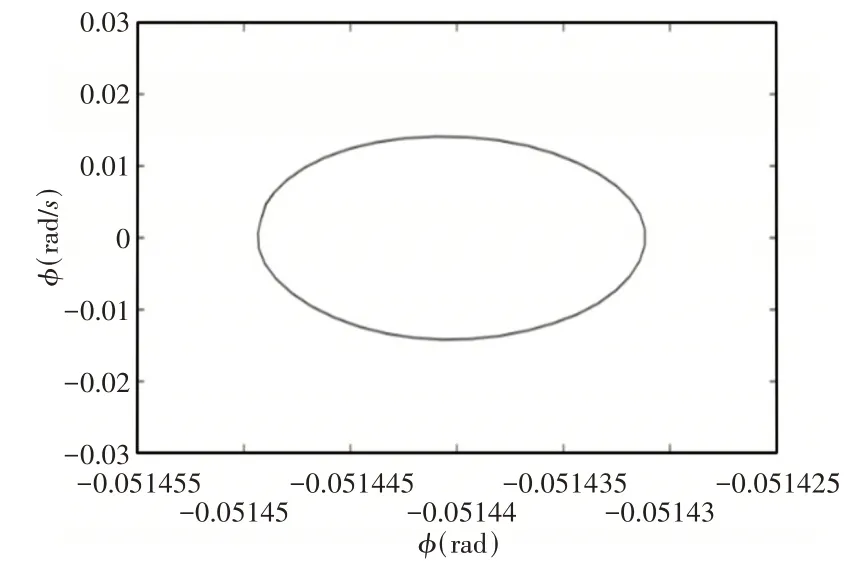
图3 后掠机翼在115m/s时的相图Fig.3 Phase Diagram of Swept−Back Wing at 115m/s
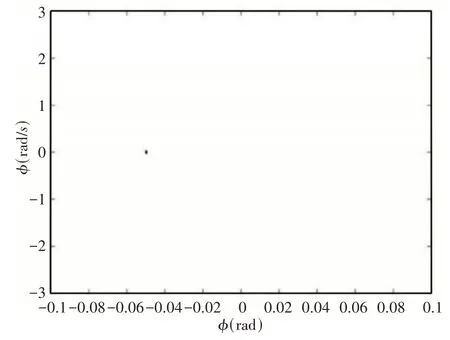
图4 后掠机翼在115m/s时庞加莱截面图Fig.4 Poincare Section of Swept−Back Wing at 115m/s
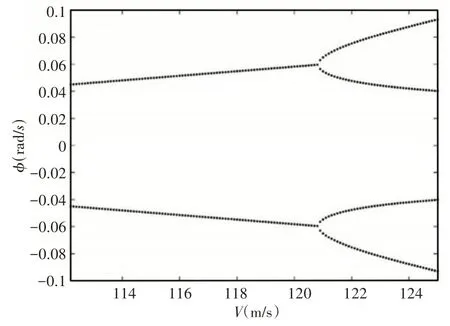
图5 具有外挂系统的后掠机翼在(112.1~125)m/s翼尖扭转角分叉图Fig.5 Swept−Back of the Wing with a Plugin System in the(112.1~125)m/s Wing Tip Torsional Angle of Bifurcation Diagram
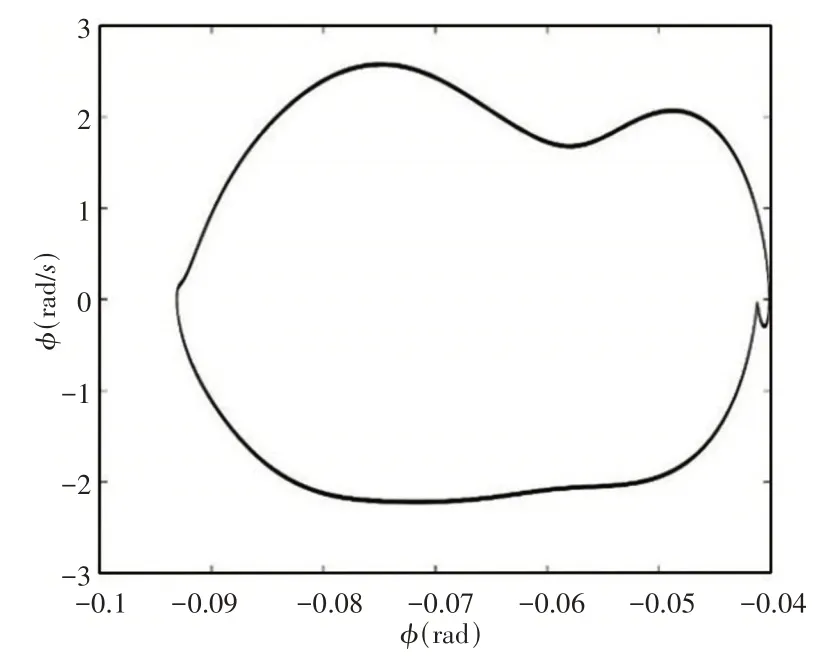
图6 后掠机翼在125m/s时的相图Fig.6 Phase Diagram of Swept−Back Wing at 125m/s
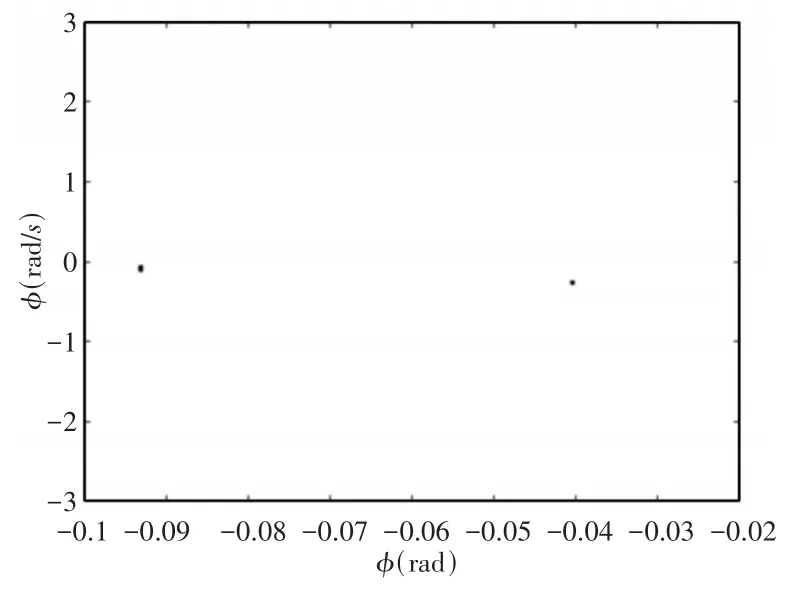
图7 后掠机翼在125m/s时的庞加莱截面图Fig.7 Poincare Section of Swept−Back Wing at 125m/s
当速度范围在(125~142)m/s时后掠机翼系统翼尖扭转角分叉图,如图8所示。由图可知,随着速度继续增大,系统从周期性的双极限环运动开始,经过周期倍化进入拟周期运动,最后进入混沌运动状态。速度为134m/s时系统的相图和庞加莱截面图,如图9、图10所示。在庞加莱截面图中由于点重合的原因使得庞加莱截面图很难辨认系统处于哪种运动状态,因此需要结合相图和分叉图综合判断,如图8~图10所示。此时系统是处于周期倍化状态的。由于在速度大于135.5m/s时系统出现了新的极限环振动,速度为135.5m/s时的相图和庞加莱截面图,如图11、图12所示。在庞加莱截面图由于点非常接近很难判断是否出现了新的极限环振动,因此需要从相图去判断,结合分叉图以及相图可知,系统此时是出现了新的极限环振动的。
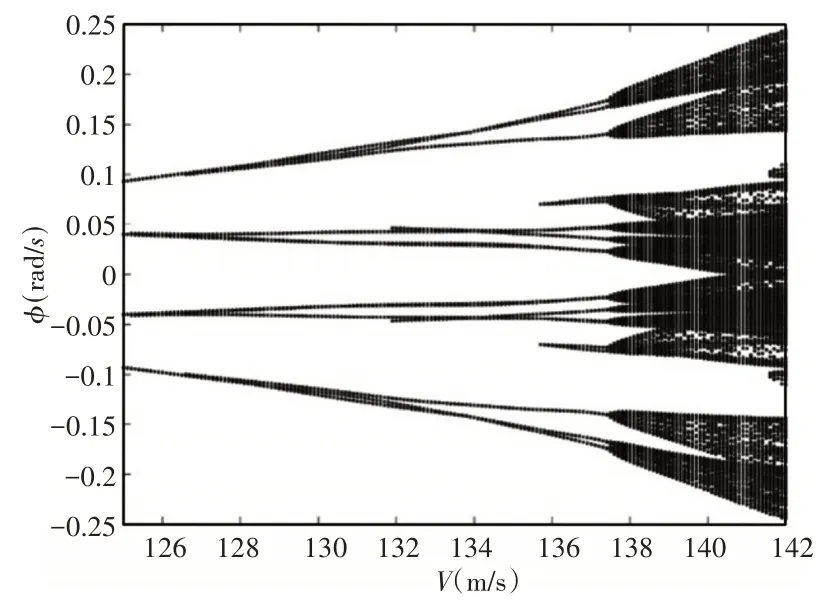
图8 后掠翼外挂系统在(125~142)m/s翼尖扭转角分叉图Fig.8 Swept−Back of the Wing with External System in the(125~142)m/s Wing Tip Torsional Angle Bifurcation Diagram
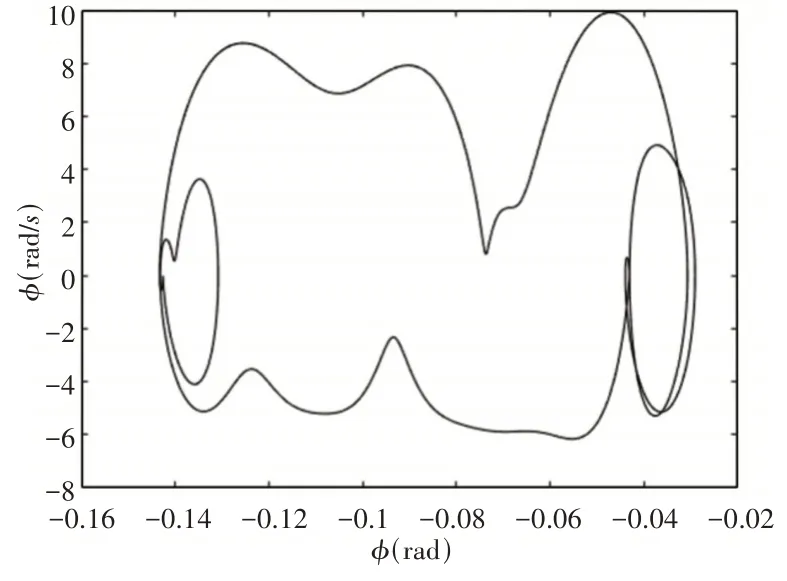
图9 后掠机翼在134m/s时的相图Fig.9 Phase Diagram of Swept−Back Wing at 134m/s
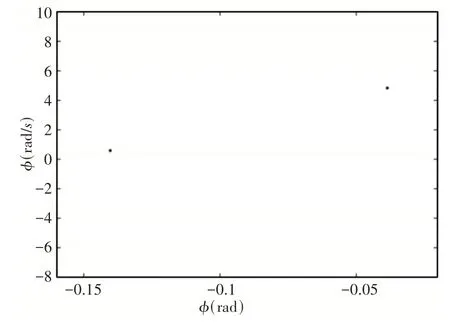
图10 后掠机翼在134m/s时的庞加莱截面图Fig.10 Poincare Section of Swept−Back Wing at 134m/s
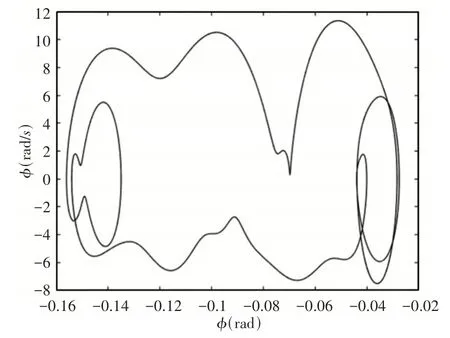
图11 后掠机翼在135.5m/s时的相图Fig.11 Phase Diagram of Swept−Back Wing at 135.5m/s
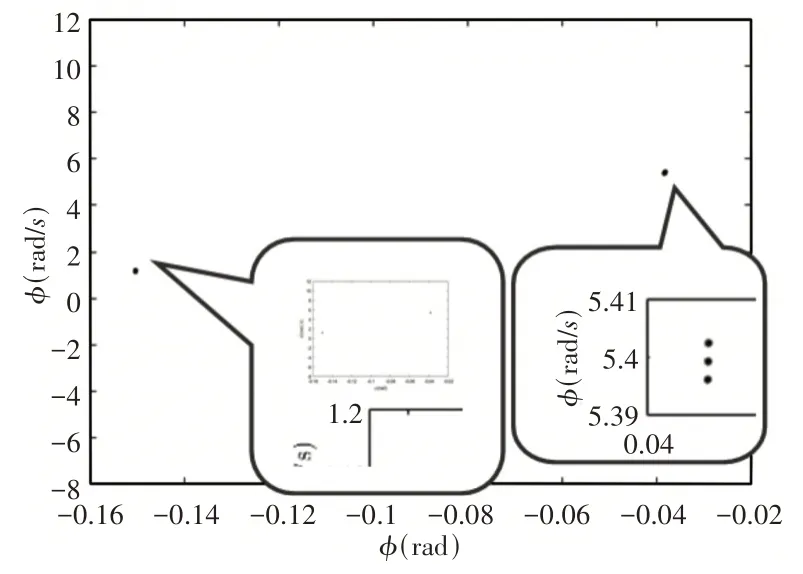
图12 后掠机翼在135.5m/s时的庞加莱截面图Fig.12 Poincare Section of Swept−Back Wing at 135.5m/s
当速度大于137.4m/s时,后掠机翼开始做拟周期运动,速度为137.5m/s时后掠翼系统的相图和庞加莱截面图,如图13、图14所示。从后掠机翼在该速度下的庞加莱截面图为封闭的曲线可知此时系统正在做拟周期运动。随着速度继续增加,由图8可知后掠翼系统将由拟周期运动变为混沌运动。

图13 后掠机翼在137.5m/s时的相图Fig.13 Phase Diagram of Swept−Back Wing at 137.5m/s
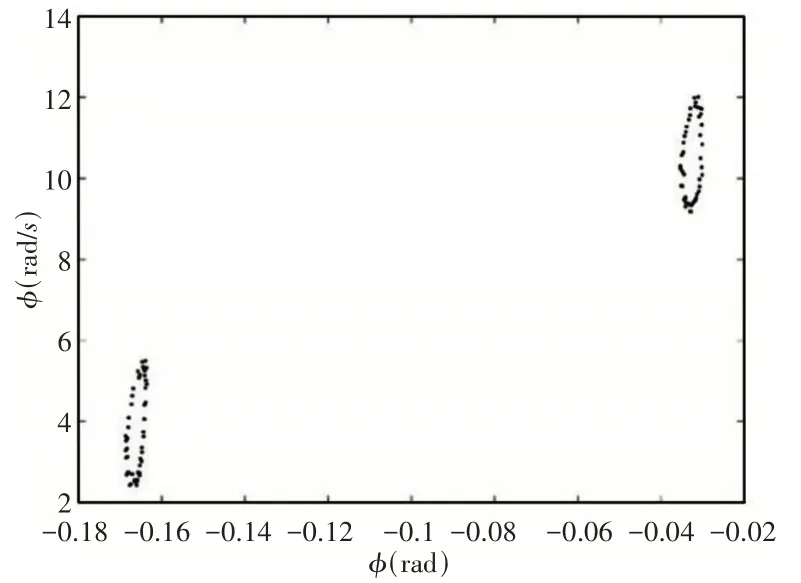
图14 后掠机翼在137.5m/s时的庞加莱截面图Fig.14 Poincare Section of Swept−Back Wing at 137.5m/s
4 结论
结合后掠翼模型分析几何非线性对后掠翼外挂系统的响应影响,得出的结论如下:
(1)当速度大于颤振临界速度96.6m/s时,后掠翼系统并没有立即进入混沌状态,而是出现极限环振动。
(2)随着速度增加,当速度大于125m/s时,后掠翼系统有单个的极限环振动变为双极限环振动。
(3)随着速度继续增加,结合相图和庞加莱截面图可知,后掠翼系统由双极限环振动进入拟周期状态。
综上所述:随着速度的增加,后掠机翼外挂系统经历了收敛、极限环振动、周期倍化运动、拟周期运动和混沌运动等一系列复杂运动状态。

