面向操纵稳定性的某越野车最优控制研究

孙传耀，顾 亮，胡 煦，田恩彤

（北京理工大学机械与车辆学院振动与噪声控制研究所，北京100081）

1 引言

随着汽车性能的不断提高，车辆操纵稳定性逐渐成为人们关注的焦点。在汽车高速行驶时，路面状态，车身惯性和侧向风等干扰因素会对操纵稳定性和安全性产生负面影响，严重时甚至可以引发事故，因此，操纵稳定性又被称为“高速车辆的生命线”［1］。在操纵稳定性的主动控制方面，一些新技术如车身电子稳定系统（Electronic Stability Control，ESC）、车身动态稳定系统（Dynamic Stability Control，DSC）和直接横摆力矩控制（Direct Yaw moment Control，DYC）等［2］，均取得了较好的效果。

国内外学者对整车操稳性控制进行了大量研究。在操稳性控制与优化方面：文献［3］提出了一种基于模型预测控制（Model Predictive Control，MPC）的主动前转向（Active Front Steering，AFS）控制策略；文献［4］设计了一种基于线性二次型调节器（Lin⁃ear Quadratic Regulation，LQR）的侧向稳定性和侧翻控制器；文献［5］采用机器学习方法并运用高斯过程（Gaussian Process，GP）回归学习车辆运动过程，改善了线性预测控制的精度，速度不足和实时性差的问题。

结合历年来国内外学者的研究情况，当前对越野车的操纵稳定性优化控制的研究中，还存在仿真工况设置不够全面以及控制方法鲁棒性差，实时性差，运算量大及优化效果不佳等不足之处。因此这里选定微型越野车为研究对象并建立了车辆二自由度理论模型，为控制器的搭建提供了理论参考。

在操稳性控制方面，设计了一种既有MPC控制器的优秀的鲁棒性和稳定性又有LQR控制器的良好实时性和响应速度的多模态混合控制器，并基于Carsim/Simulink搭建了虚拟试验联合仿真平台，对两种操纵稳定性测试工况进行了仿真试验。

2 整车操纵稳定性动力学理论建模

对车辆的操稳性进行研究时，横向与横摆运动是最为重要的研究对象，并且是后文中控制器设计的理论依据［6］，因此建立了二自由度自行车模型，如图1所示。

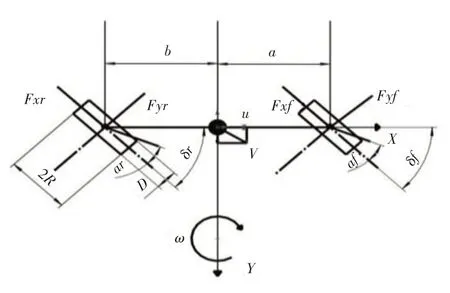
图1 车辆二自由度自行车模型Fig.1 Vehicle 2 DOF Bicycle Model

二自由度模型为［7］：

式中：a，b—质心到前后轴的距离；β—质心侧偏角；k1，k2—前后轮等效侧偏刚度；δ—前轮转角；Vx—纵向速度；ωr—横摆角速度；Iz—横摆转动惯量；m—车辆总质量。

3 车辆操纵稳定性控制器设计

3.1 模型预测控制器基本原理概述及设计

模型预测控制的核心思路为：模型预测，滚动优化以及闭环反馈修正。其具体执行步骤为：设当前时刻为k，MPC的预测时域与控制时域分别为P和C；设置控制系统的约束，求出系统在［k，k+P］范围内的预测输出值；将预测输出值与期望输出值相比较，根据其差异及约束条件求出系统在［k，k+C］中的最优控制结果；更新系统状态，进行下一轮控制。据此循环即可求出全局最优解［7］。设计MPC控制器原理，如图2所示。

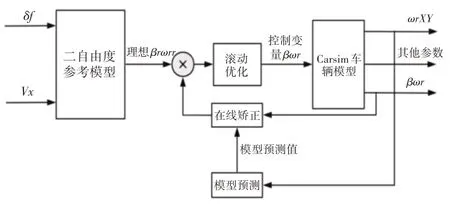
图2 MPC控制器原理图Fig.2 Schematic Diagram of MPC Controller

根据上文中的线性二自由度模型的动力学方程式（1）、式（2）可知，横摆角速度，横向速度及质心侧偏角参考值如下：

式中：K—稳定性系数

由上文中所建立的线性二自由度理论模型式（1）、式（2）可知，选定质心侧偏角β和横摆角速度ωr为状态变量，构建该模型的状态空间方程如下：

式中：状态变量X=[β，ωr]T；输入变量为I=δf；

输出变量—O=[δf，δr]T；这其中δf，δr—车辆前后轮转角。

MPC控制器的目标函数如下：

式中：NP，NC—控制时域和预测时域；Δη(t+i|t)—车辆实际的状态变量输出与理想参考值的差值；Q，R—权重矩阵。约束条件如下：

因此，所设计的MPC控制器需要在每一控制周期内解决如下优化问题：

式中：yh，ys—硬约束和软约束；yh，min、yh，max和ys，min、ys，max—各自的极值。综上，即可将该问题转化为二次规划问题，从而实现系统的MPC最优控制。

3.2 线性二次型控制器基本原理概述及设计

LQR（Linear Quadratic Regulator）即线性二次型调节器，是现代控制系统中应用最广泛，最优控制效果最突出的控制方法之一，具有响应速度快，鲁棒性强等优势。LQR的控制对象为以状态空间形式给出的线性系统，其控制基本思路是由空间状态参量A，B以及状态参数Q，R确定最优反馈增益矩阵K，而K则使LQR的控制目标函数J取得最优解［8］。

由上述原理，设计LQR控制器原理，如图3所示。

图3 LQR控制器原理图Fig.3 Schematic Diagram of LQR Controller

在上一节所求出的线性二自由度模型的状态空间方程式（6）的基础上，设该系统的误差矢量为：

式中：Or—该系统的期望输出。

线性二次型调节器的目标函数为：

式中：Q与R互为正定对称时变矩阵。

根据数学原理列写上述系统的Hamiltonian函数如下：

式中：λ—Lagrange乘子。

若要使J取得最小值，则控制目标转化为使H取得极小值，因此：

经推导得：

式中：IB—最优输入；P—对称正定常数矩阵；g—常数伴随矩阵。

P与g满足如下方程组：

最后寻找出最优的输入IB，使得LQR的目标函数的实际输出O在某一时间段内最接近期望输出Or即可。

至此，越野车操纵稳定性线性二次型调节器设计完成。

3.3 基于MPC与LQR的多模态混合控制器设计

无论是模型预测控制器还是线性二次型控制器，从理论上都能够实现改善操纵稳定性的目的，但在车辆的实际行驶过程中，在路况，天气以及驾驶员的操作等种种因素的影响下，车辆的运动非常复杂，单纯用某一种控制器对操纵稳定性进行控制具有比较明显的局限性，无法兼顾多种工作情况，进而导致控制器的控制效果变差，并且这种局限性在越野车中会更加明显。因此，需要综合考量各个控制方法的优缺点，设计多模态混合控制器，以便更好地适应车辆实际工作中的各种情形。

所以，针对上述问题，结合前文设计的MPC 控制器和LQR控制器，这里设计了一种基于上述两种最优控制器的混合控制器，考虑到MPC控制器控制稳定可靠，超调量小和运算量小的特点，在路况较好或直线路面上，采用MPC控制器对越野车操纵稳定性进行控制；考虑到LQR控制器实时性好，鲁棒性强以及精度高的优点，在崎岖路面或弯道路面上，切换至LQR控制器对操纵稳定性进行控制。基于MPC和LQR的多模态混合控制器的原理图，如图4所示。

图4 多模态混合控制器原理图Fig.4 Schematic Diagram of Multimodal Hybrid Controller

由式（1）、式（2）可得线性二自由度理论模型的理想横摆角速度和质心侧偏角为（3）、（5），选择横摆角速度为控制对象。

设某一时刻和上一时刻横摆角速度的差值为：

令横摆角速度差值的阈值为Εω，则：

当∆ωr≥Εω时，判定为崎岖路面或非直线路面，协同控制器切换到LQR控制器对越野车操纵稳定性进行控制；当∆ωr<Εω时，判定为平缓路面或直线路面，协同控制器切换到MPC控制器对越野车操纵稳定性进行控制。控制器下达决策后，通过控制车辆的转矩分配等方式从而控制车身横摆力矩来对与理想值有偏差的操纵稳定性参数进行矫正。

4 基于Carsim/Simulink的操纵稳定性联合仿真平台搭建

Carsim是当前汽车仿真应用最为广泛的车辆动力学仿真软件之一，其模型有二十七个自由度，具有精度高，虚拟试验工况齐全，可拓展性好，交互性强等优势，常被用来进行车辆的虚拟试验，其结果与实车试验数据差距很小，因此可信度非常高。因此，这里车辆模型由Carsim提供，联合仿真模型，以及MPC与LQR的混合控制模块等由Simulink搭建，仿真试验步骤如下：

（1）在Simulink中分别建立MPC和LQR模块，并根据上文的理论搭建基于MPC与LQR的多模态混合控制器模型，所搭建的联合仿真模型，如图5所示。

图5 Carsim/Simulink联合仿真平台Fig.5 Casim/Simulink Joint Simulation Platform

（2）在Carsim/Simulink 联合仿真平台中对整车参数进行设置［9−10］，如表1所示。Carsim参数设置，如图6所示。

表1 微型越野车操纵稳定性模型参数符号含义及赋值表Tab.1 The Meaning and Assignment Table of the Param⁃eters of the Handling and Stability Model of the ORV

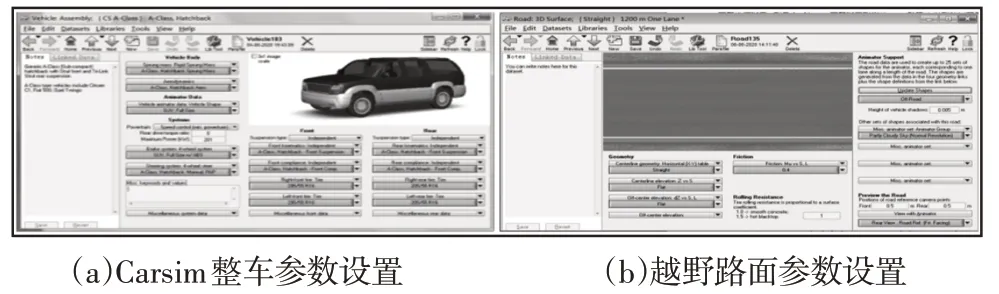
图6 越野车Carsim参数设置Fig.6 ORV Carsim Parameters Setting

（3）在Carsim中设置越野路路况参数，并对双移线工况和转向盘角阶跃输入工况的方向盘转角曲线进行设置［9−10］。

5 整车操纵稳定性联合仿真仿真试验结果对照及分析

双移线（Double Lane Change，DLC）工况是指汽车在两次连续变道操作后最终回到原来车道的操稳性试验方法［7］。仿真试验取初速度为72km/h。需要研究的操纵稳定性参数如下：侧向、垂向加速度、车身侧倾角和横摆角速度，如图7所示。

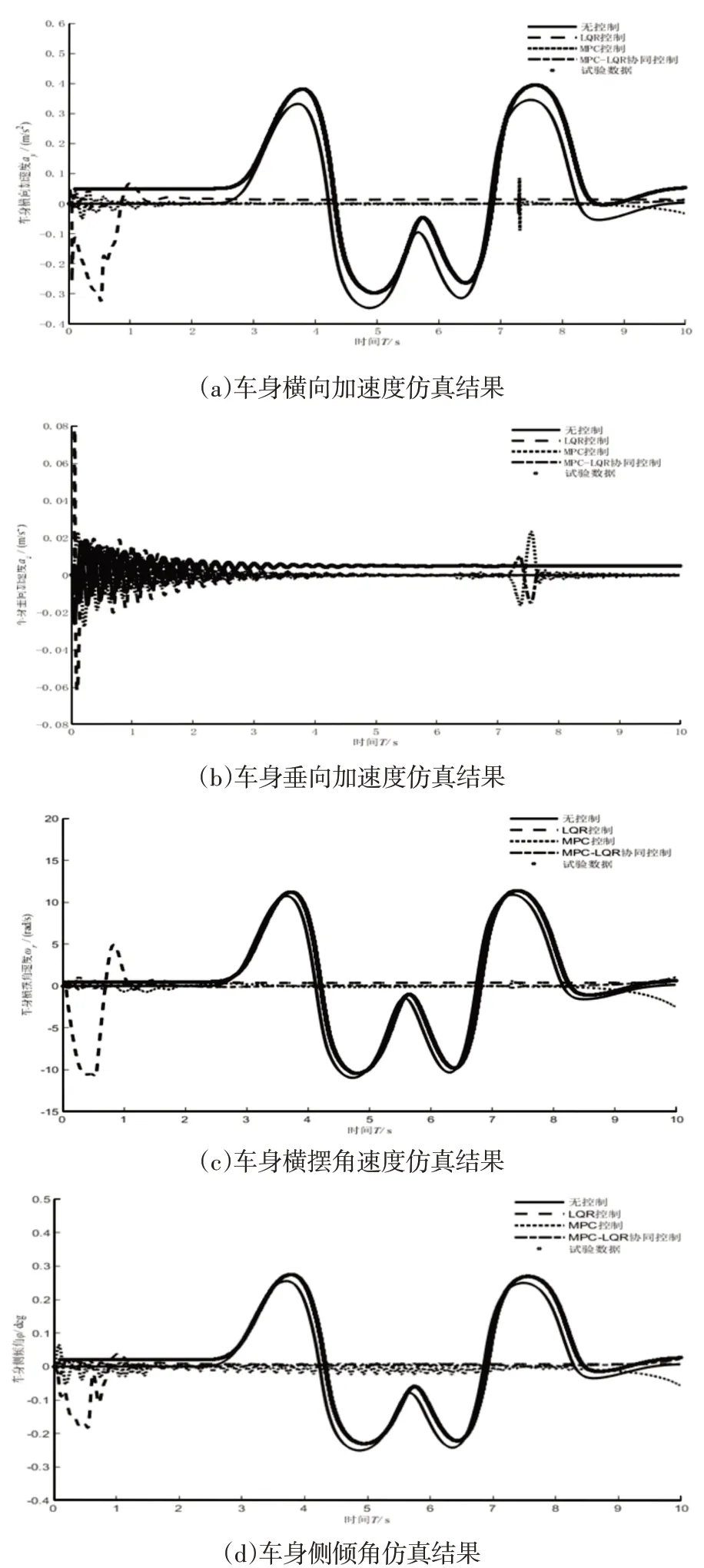
图7 DLC工况下车身操稳性指标（图a至d）仿真结果对照图Fig.7 Comparison of Simulation Results of Body Handling Stability Index（Figure a to d）Under DLC Condition

转向盘角阶跃输入工况指方向盘输入为阶跃信号的工况。在此工况下，汽车先匀速直线行驶，后急打方向盘至某一固定角度后保持不变［7］，取初始速度为72km/h。需要研究的操稳性变量如下：车身侧向、垂向加速度，车身横摆角速度与侧偏角，如图8所示。在图7与图8中，将实车试验结果拟合曲线与这里所搭建的整车虚拟样机模型仿真结果曲线进行对比可知，这里所搭建的车辆模型能够比较精确地描述车辆实际行驶时的状态。

图8 转向盘阶跃输入工况下车身操稳性指标（图a至d）仿真结果对照图Fig.8 Comparison of Simulation Results of Body Handling Stability Index（Figure a to d）Under Steering Wheel Step Input Condition

这里所设计的多模态控制器的控制机理是：首先，在图4的模态切换规则下，由图2、图3可知，控制器首先在前轮转角和纵向初速度输入下由二自由度参考模型计算出车辆的参考质心侧偏角与横摆角速度；随后Carsim模型在初始输入条件下输出得到越野车的质心侧偏角与横摆角速度的仿真值；在LQR模态下，质心侧偏角和横摆角速度的参考值与仿真值的差值将作为控制参数，由控制器计算得出理想的前轮转角值，并在下一时刻进行矫正，如此循环，实现对越野车操稳性的改善；在MPC 模态下，由Carsim模型的仿真横，纵向位移及横摆角速度作为模型预测参量得出横摆角速度与质心侧偏角的模型预测值，并根据二者的仿真值对模型预测值进行在线矫正，随后将二者矫正后的模型预测值与其参考值作为输入量进行滚动优化，将得到的理想横摆角速度与质心侧偏角反馈给Carsim模型，在下一时刻进行矫正，如此循环，实现对越野车操纵稳定性的改善。

在上述控制机理的执行下，仿真结果，如图7、图8所示。由图可知，无论在双移线工况还是转向盘角阶跃输入工况下，采用了优化控制器的仿真操纵稳定性指标试验结果的绝对值明显小于无控制的情况下的绝对值，且仿真曲线收敛速度快，超调量小，波动较少，说明了无论是哪一种控制器，都能在一定程度上显著改善越野车的操纵稳定性。

在MPC控制下，操纵稳定性参数的波动更小，幅度更小，的控制效果明显优于LQR控制，基于MPC和LQR的多模态混合控制则更好地继承了上述两种控制器共同的优点，对操纵稳定性的优化控制效果明显强于MPC控制器和LQR控制器，参数曲线能够在波动幅度最小的前提下，以最快的响应速度，最小的波动频率迅速收敛于接近零的位置，这说明多模态混合控制器对越野车操纵稳定性的控制起到了良好效果。

6 结论

这里首先建立了两种车辆运动学理论模型，为文中操纵稳定性参数的分析以及控制器的设计提供了理论依据；然后建立线性二自由度车辆模型的状态空间方程并据此设计了MPC操稳性控制器，LQR操纵稳定性控制器以及基于MPC和LQR的多模态混合控制器；随后根据联合仿真的思想搭建了基于Carsim/Simu⁃link虚拟试验平台，进行了两种典型工况的仿真实验，根据仿真结果对所设计的控制器性能进行了评价。结果表明，所设计的多模态混合控制器能够有效地实现车辆的横向与垂向加速度的优化，对横摆角速度和车身侧倾角的优化效果也较为显著，二者均有幅度小，响应速度快，迅速收敛于安全范围的特征，且上述操稳性指标的控制效果均明显优于单纯使用MPC或LQR控制器时的情况，因此该控制器能有效的防止车辆出现侧翻，侧滑和甩尾等安全事故且能减缓轮胎系统以及其他易耗元件的过度磨损，对越野车的操纵稳定性控制具有积极意义。