指向问题解决的高中物理结构性思维教学策略——以斜面上斜抛运动的思维分析为例

简伟伟

(江西省横峰中学)

一、指向问题解决的高中物理结构性思维的概述

就高中物理的学科教学而言,因为高中物理问题逻辑关系复杂、知识综合性强、思维分析要求高,根据结构性思维逻辑思路清晰、问题本质指向明确、知识调度多维的特点,我们在物理教学中可以通过培养学生的结构性思维方式来提升学生的问题解决能力。在培养学生结构性思维的具体教学过程中,我们要引导学生以指向问题解决的目标为导向、抓住问题的本质、厘清问题中各变量的关系、充分调动各类知识、寻找最优认知结构,构建问题解决的最优路径,最终实现目标的高效达成。

下面笔者以一道典型的抛体问题的解答为例,讲述如何设计问题、引导学生有序思考,培养学生的结构性思维。

二、指向问题解决的结构性思维教学案例

【例题】如图1所示,从倾角为θ的足够长的斜面上顶点,以初速度v0与水平方向成α斜向上抛出一个小球,不计空气阻力。求:

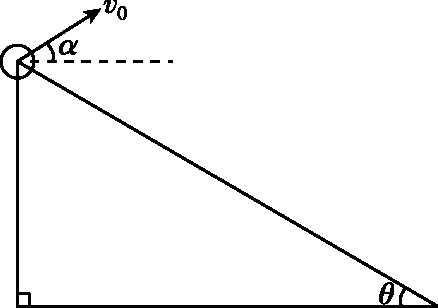
图1

(1)从抛出开始经过多长时间小球运动到最高点?

【结构性思维分析】

目标导向：经过多长时间小球到达最高点?

结构性思维流程：①怎样的位置是最高点?②最高点有什么物理特征?③怎样可以方便找到这样的位置?

指向问题解决的结构性思维路径：默认意义上的最高点是相对水平面而言的,因此该问题我们以水平和竖直两个方向建立平面直角坐标系,对解决问题较方便。我们知道,只要小球的速度在竖直方向有向上的分速度时,小球将继续向上运动,因此当小球竖直速度为零时小球便到达最高点。我们分别求出竖直方向的初速度及加速度便可以较简单地求出相应的时间。

如图2所示,根据vy=v0sinα-gt=0,即可求出小球到达最高点所需的时间。

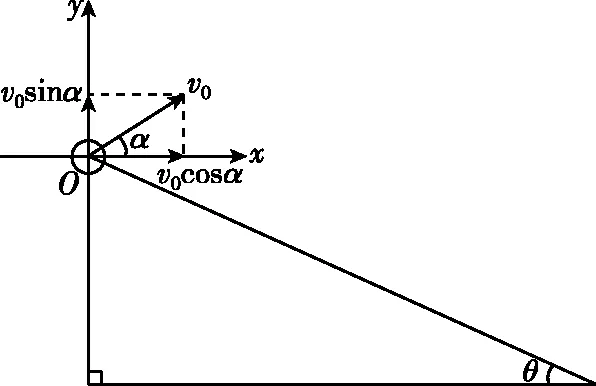
图2

(2)从抛出开始经多长时间小球离斜面的距离最远?

【结构性思维分析】

目标导向：经过多长时间小球离斜面的距离最远?

结构性思维流程：①小球在怎样的位置离斜面的距离最远?②小球离斜面的距离最远的位置有什么物理特征?③怎样可以方便找到这样的位置?

指向问题解决的结构性思维路径：如图3所示,要分析小球离斜面最远的位置,我们应该从平行斜面和垂直斜面两个方向上来思考问题,当小球在垂直斜面上有向上的分速度时,小球沿垂直斜面方向将继续上升,因此当垂直斜面上的分速度变为零时便是小球运动离斜面最远的位置,我们分别求出这两个方向上的初速度和加速度便可以求出相应的时间。

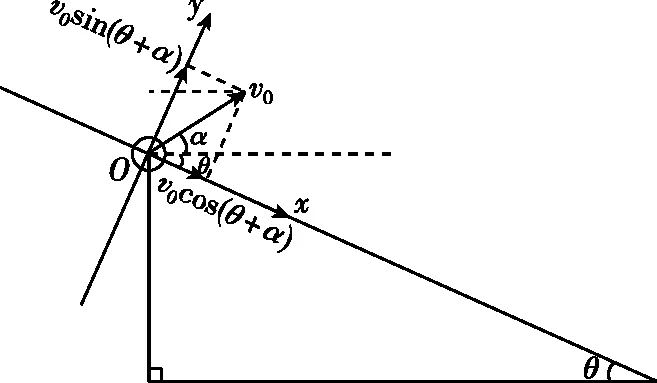
图3

如图3所示,根据vy=v0sin(θ+α)-gcosθ·t=0,即可求出距离斜面最远所需的时间。

(3)从抛出开始经多长时间小球速度最小?

【结构性思维分析】

目标导向：经过多长时间小球的速度最小?

结构性思维流程：①小球做什么类型的运动?②为什么小球的速度有最小值?③怎样可以方便找到这样的位置?

指向问题解决的结构性思维路径：因为小球抛出后只受重力,小球水平方向速度不变,水平方向分运动为匀速直线运动;竖直方向分运动为匀变速直线运动。当小球竖直速度为零时,小球的合速度为最小值。因此,该问所求的时间和小球到达最高点的时间是相同的。

(4)小球离斜面最远时距离出发点的水平位移?

【结构性思维分析】

目标导向：小球离斜面最远时距离出发点的水平位移?

结构性思维流程：①小球做什么类型的运动?②问题(2)中的位置和本问题是同一个位置,其对我们解答本问题有没有帮助?③问题(2)中已经知道了经过多长时间小球距离斜面最远,我们如何确定这段时间的水平位移?

指向问题解决的结构性思维路径：根据第(2)问在沿斜面及垂直斜面方向的直角坐标系中的分析我们已经知道了小球经过多长时间距离斜面最远,因为题中求这段时间内的水平位移,我们再转换思维,回到水平竖直坐标系,因为小球在水平方向的分运动是匀速直线运动,我们结合小球的水平分速度便可求出这段时间内小球的水平位移。

根据vy=v0sin(θ+α)-gcosθ·t=0和x=v0cosα·t二式联立便可求出小球离斜面最远时距离出发点的水平位移(在两个坐标系视角下综合分析问题)。

(5)以斜面顶点为坐标原点,水平向右为x轴正方向,竖直向上为y轴正方向建立平面直角坐标系,求小球在该坐标系下的轨迹方程?

【结构性思维分析】

目标导向：小球在该坐标系下的轨迹方程?

结构性思维流程：①什么是轨迹方程?②如何确定小球在题中坐标系下的轨迹方程?

指向问题解决的结构性思维路径：如图4所示,轨迹方程就是该坐标系下y随x的变化关系,我们可以分别找出x、y随时间t的变化关系,再消去参数t,找到y随x的变化关系,就可以确定轨迹方程。

图4

x=v0cosα·t

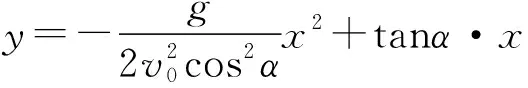
(6)小球落在斜面时距离出发点的水平位移?

【结构性思维分析】

目标导向：小球落在斜面时距离出发点的水平位移?

解法一:结构性思维流程：①小球做什么类型的运动?②小球落到斜面上有什么关键的特征?③如何根据以上特征求出所求量?

指向问题解决的结构性思维路径：我们从平行斜面和垂直斜面两个方向上来思考问题,小球落到斜面上即小球在垂直斜面方向上的位移为零,在该坐标系中可简便求出小球落到斜面上的时间,再转回水平竖直坐标系,根据斜抛运动在水平方向的分运动为匀速直线运动的特点可以求出其距离出发点的水平位移。如图3所示,根据

x=v0cosα·t

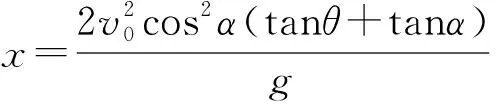
解法二:结构性思维流程：①小球做什么类型的运动?②问题(5)中已经知道了小球的轨迹方程对求小球落在斜面的位置有没有作用?③如何根据轨迹方程确定小球落在斜面的位置?

指向问题解决的结构性思维路径：如图5所示,根据第(5)问我们知道了小球运动的轨迹方程,我们在同一坐标系中找到斜面的轨迹方程,二者联立找到交点,即为小球落到斜面的位置。根据

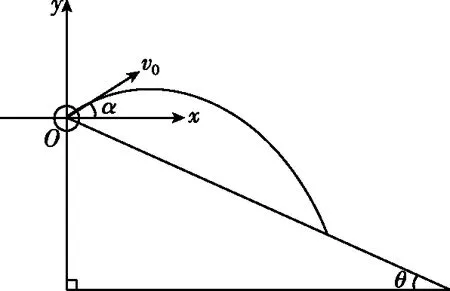
图5

y=-tanθ·x

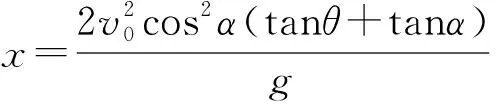
三、指向问题解决的结构性思维教学的设计意图分析

在教学实践过程中,基于斜面上的斜抛问题笔者设计了六个典型问题,问题与问题之间具有一定的联系,又具有层级的递进关系。笔者在教学过程中引导学生根据结构性思维的思维方式思考问题,后面的问题以前面的问题为“台阶”,在逐个问题的分析、思考、解答过程中,训练、巩固结构性思维的思维方式,培养学生的结构性思维素养。具体细节设计中,每一个问题有一个明确的目标指向,教学过程中引导同学们根据问题的目标指向,确定突破的方向,然后根据选定的方向,规划问题解决的最优路径。同学们在问题解决的目标指引下,有序地思考,清晰地表达,高效地解决问题。教学实践证明,同学们通过对本题六个问题的思考、分析,深刻领悟到结构性思维的基本要领。这种教学策略对培养同学们的结构性思维具有良好的实践意义,同时实践证明,结构性思维的思维方式能为物理问题的解决规划高效的思维路径,实现物理问题的高效解决。