2023高考全国乙卷物理25题的九种解法

王洪亮 谢春树

(1.江苏省镇江心湖高级中学;2.江苏省连云港市灌云县教师发展中心)

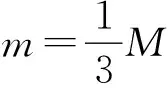
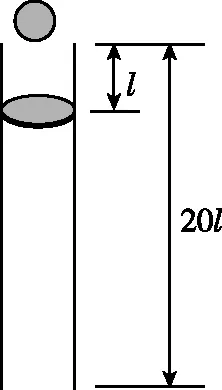
图1

(1)第一次碰撞后瞬间小球和圆盘的速度大小;

(2)在第一次碰撞到第二次碰撞之间,小球与圆盘间的最远距离;

(3)圆盘在管内运动过程中,小球与圆盘碰撞的次数。

方法一:运动分段法

方法二:运动过程的整体法

方法三：v-t图像法

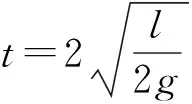
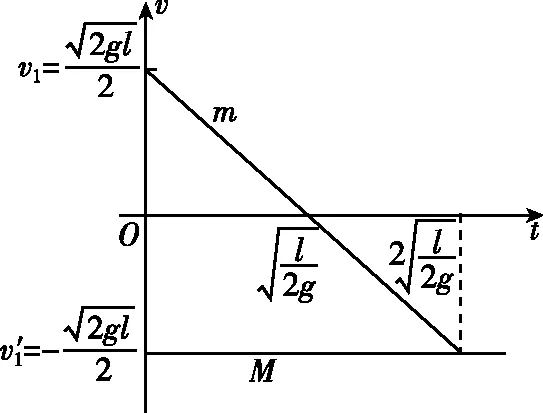
图2

方法四：x-t图像法

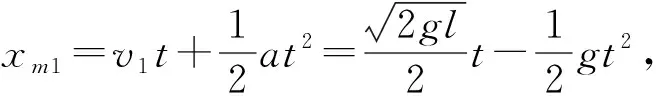
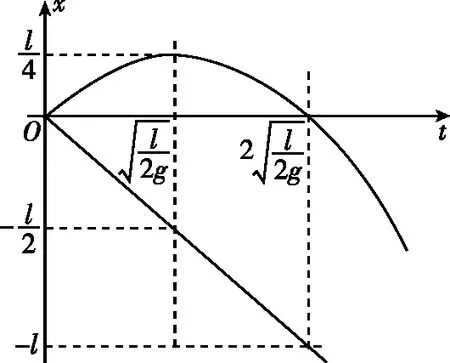
图3

方法五:相对运动速度—位移公式法

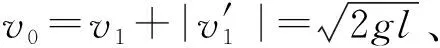
方法六:相对运动速度与时间、位移与时间关系法

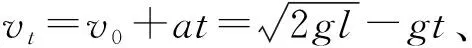
方法七:相对运动的v-t图像法

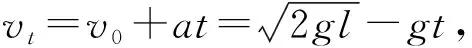
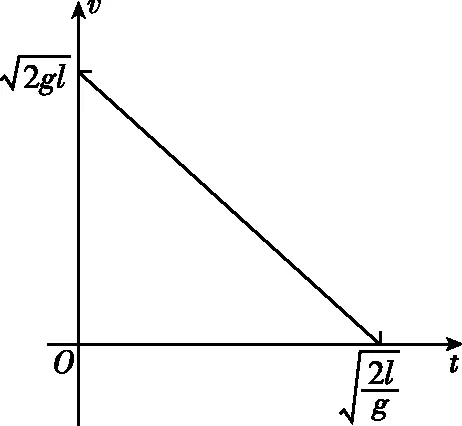
图4

方法八:相对运动的x-t图像法

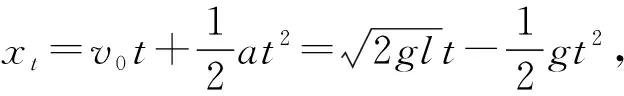
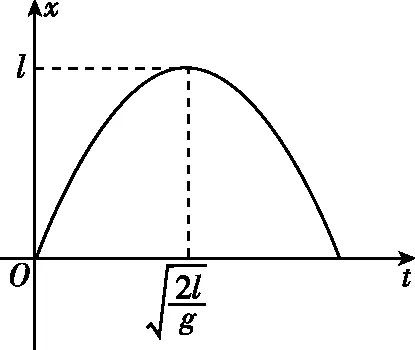
图5

方法九:用数学函数求极值

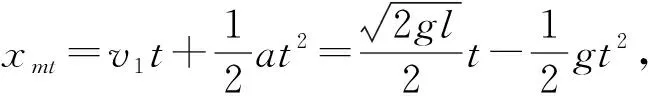
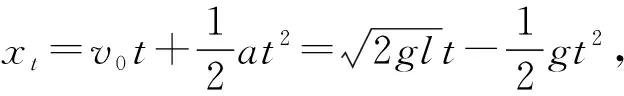
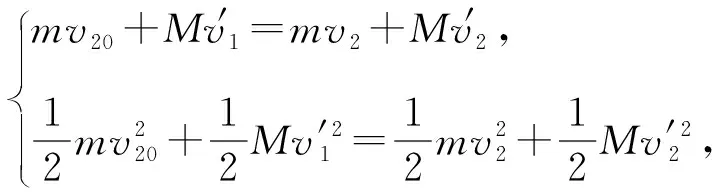
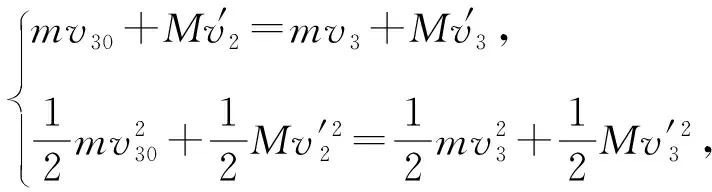
对比小球第一次、第二次、第三次与圆盘碰撞后圆盘沿管壁移动的距离Δx12=2l、Δx23=4l、Δx34=6l,可得小球第n次与圆盘碰撞后圆盘沿管壁移动的距离必为Δxn(n+1)=n×2l,其中n为正整数;要使圆盘与小球发生第n次碰撞后从管口离开则必满足Δx12+Δx23+Δx34+…+Δxn(n+1)≥20l-l,即2l+4l+6l+…+2nl≥19l,即n≥4,故圆盘在管内运动中小球与圆盘只能碰撞4次。

【总结】此题是历年高考中的传统经典类题目,是运动学、动力学、弹性碰撞中动量守恒定律与机械能守恒定律综合应用的大分值题,由于此类问题过程复杂、变化多样、关键状态多、相应的物理量多,因此一定要注意各次碰撞中的物理量正确对应,规定正方向后各物理表达式中速度的正、负符号要用正确,每次计算结果的合理取舍及相应正负号的实际意义须明确;对竖直上抛运动过程的处理要灵活选择合适的参照物,正确选择分段法、运动整体法、相对运动法、图像法、数学函数法,仔细分析清楚每段过程的运动情况,结合题目提供的条件寻找出正确的结果;因此我们在平时教学中一定要注意作好物理过程的认识与分析、物理量正、负号的正确应用、匀变速直线运动知识的灵活选择与运用、数学物理知识的有机结合等,才能提高学生准确理解、分析、综合归纳及正确解答实际问题的能力,使我们的教学达到优质的效果。