高等数学教学中学科融合的一些思考——高等数学与工程制图教学的结合

韩华

(天津理工大学理学院,天津 300382)

随着科学技术的迅速发展和计算机技术的广泛应用，数学的思想、方法以及技术在自然科学、工程技术等领域发挥着越来越重要的作用，而且已经广泛深入到经济学、管理学以及社会学等各个相关领域。大学生也需要在高等数学的学习中获得更丰富、更有用的现代数学知识，提升运用数学工具和技术的能力，以适应现代社会的发展。高等数学是本科生学习阶段的一门必修课，高等数学课程的学习质量是本科生学习水平的一个重要标志，也是学生由中学阶段向大学阶段角色转换过程中遇到的第一块试金石。所以，教师和学生之间互相配合、教学相长，是提高学生学习的积极性和提升教师的教学水平的双赢策略。

高等数学课程中所学习到的微积分知识，是理工科学生的专业课学习阶段的重要工具，也为相关课程的开展提供了专业的知识储备，所以理工科学生的高等数学学习显得尤为重要。但是我们始终认为，大学数学的教育目标不应该仅仅是为学生专业课的学习提供理论基础，在教学的过程中更重要的是引导学生接受数学文化的熏陶，学会一种理性的思维模式。在其脑海中搭建一座桥梁，把所学的知识在思想中融合，做到融会贯通，游刃有余。

本科生第二学期的高等数学教学，涉及重积分的计算以及曲线曲面积分的计算。这是高等数学教学的重点也是难点，是理工科学生后续学习必须具备的基本计算能力。但是，大部分的学生并没有相关的绘图基础，没有办法具体地刻画出相关的三维图形。这使得三重积分以及曲面积分的计算中，向相关平面的投影图形的形状难以理解，导致后续的计算无法进行。所以在教学过程中，我们尝试利用各种工具来帮助学生画好三维图形，这样可以更直观、更深刻地理解投影到某个面上的投影区域的划定，也能够帮助学生更好地学习曲面积分的知识。

事实上，在工科专业学生的教学中，对三维图形的描绘，学生反而显得尤为感兴趣，在了解到他们上个学期的工程制图课程也涉及三维制图后，笔者在教学设计里，由一道习题引入，将高等数学和工程制图的教学相结合，激发了学生的学习兴趣，让学生对相应内容的理解更加深刻，也体现了当前多学科交叉融合的教学特点。

一、问题的引入

第一类曲面积分的运算，主要涉及以下内容，设积分曲面Σ 由方程z=z(x，y)给出，Σ 在xOy面上的投影区域为，函数在上具有连续偏导数，被积函数f(x，y，z)在Σ 上连续。则由分析可得

这样就把对面积的曲面积分化为了向坐标平面xOy投影下的二重积分。同样，若曲面Σ 由x=x（y，z）方程或y=y（z，x）给出，我们也可以类似地把对面积的曲面积分化为向坐标平面yOz或者zOx投影下的二重积分进行相应计算，公式分别为：

显然，如何确定向各个平面投影的函数图像是曲面积分求解问题的关键，在遇到第一类曲面积分时，如何确定向哪个平面投影也是学生纠结的问题。

二、问题过程分析

这道题求解并不困难，但是由于锥面被曲面切割部分的具体形状比较难以想象，学生在具体的求解过程中产生了疑问。对于该问题，课后习题给出的标准答案是向xOy平面做投影，如图1所示，Σ 在xOy面上的投影区域为圆形区域，由计算曲面积分公式：

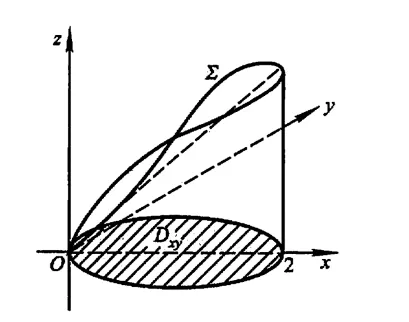
图1 投影图

在教学过程中，学生对这个图形非常感兴趣，经过课堂讨论，学生产生了以下的疑问：

第一，向xOy平面投影，投影区域就是一个圆，能否把这个具体的投影过程用3D图像刻画出来？

第二，分别向xOz，以及yOz平面投影，对应的投影区域是什么样子的，又如何计算？计算过程相比较是不是会更简单？

由于材料工程类专业的学生在专业基础课学习“现代工程图学”课程中，该课程主要教授学生研究绘制和阅读工程图样的原理和方法，而这些是工科学生必备的表达和交流工程技术思想的重要工具。该课程对现代流行的经典计算机绘图软件AutoCAD有了一些了解，学生很快利用CAD制图将立体图形画出，如图2所示。这个图形能够直观地看到两个曲面的交线，学生能够通过自己的相关专业知识来解决数学问题。由于要分别向三个坐标平面投影，如果三维图形能够更直观地演示出投影区域，将更容易帮助计算。作为课外作业，学生也饶有兴趣地去寻找相关的作图软件，并得到了想要的效果[1-3]。

图2 Auto 作图

通过查阅资料，学生发现了一款非常好用的3D绘图软件GeoGebra，这是一款非常实用的数学作图软件。在中小学教学中广泛使用，可以用来几何作图、函数绘图、代数演算等。在课堂演示教学，课后作业的完成中起到了很好的作用，使得教学过程更立体、更生动并富有启发性，让学生印象深刻，理解更到位，在方便学生的同时，也提升了教师的工作效率。

对我们来说，这款软件最大的优点就是可以动态地展示各类立体几何图像，无论图像位于哪个平面，都可以直观地观看，并且可以逐步展示投影的过程，让学生的思维豁然开朗。在简单学习这个软件的基本应用后，学生直观地得到了曲面Σ 的3D图像，如图3所示。

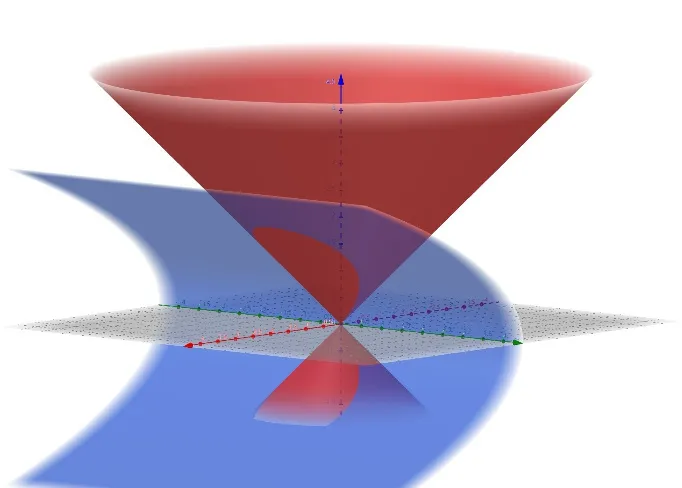
图3 GeoGebra 绘制的3D 图形

接下来，通过将该3D图像进行旋转，我们得到了该曲面分别向三个坐标平面上的投影区域，如图4，图5所示，并利用这些图形给出了分别向xOz，以及yOz平面投的计算过程。向xOz面投影的计算过程：

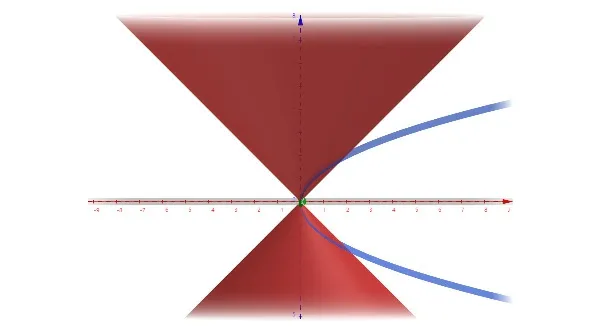
图4 向xOz 面投影图像

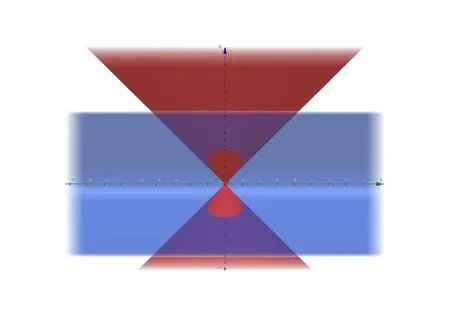
图5 向yOz 平投影图像

从这个图像上很明显看得出对称关系，我们只需要计算在第一象限里的投影，最后取2倍即可（题目只有上半部分的图像）。计算过程如下：

向yOz面投影的计算过程：

这个计算也涉及到了对称性，同样我们可以只求第一象限再取2倍。这个计算主要麻烦在投影区域边界方程稍微复杂一点，学生在求解二重积分时需要的计算量大一些。主要计算过程如下：

在分析和演算的过程中，学生也发现了，向每个平面投影的计算复杂度都有差别。特别是第三个向yOz平面的投影，计算的复杂程度很大，计算也用到了较多的定积分求解技巧，稍有不慎，整个过程就需要从头演算。对于这道题来说，向xOy平面投影的计算是最简单的。

在学生对两个软件都熟悉后，我们把整节课的相关图形，都用AutoCAD和GeoGebra做了刻画。特别是GeoGebra的使用，使得学生更加乐意去尝试向不同的平面去做投影，进一步地发现向哪个平面的投影计算更加简单，学会了第一类曲面积分的一个计算技巧，理解了第一类曲面积分的意义。这节课的教学内容本来是高等数学教学中的一个难点，对于三维图形的空间想象力的限制，使得学生理解和计算上都存在着困难。但是机缘巧合的我们找到了学生的一个兴趣点，将整节课的教学内容加以拓展，使整个课堂对学生的吸引力更大，内容更加充实丰富，学生获益良多。

三、主要思想总结

这道题目的选取其实非常合适，既让学生了解了向不同平面投影的区别，又在整个计算过程中训练了学生的水平，并且对之前定积分的不同类型的计算做了复习。让学生直观了解了曲面积分和二重积分的区别和联系，为进一步地讲解第二类曲面积分，以及两类曲面积分之间的关系做了很好的铺垫。

关于多重积分的学习，一直是高等数学教学过程中的重点和难点，由于所学知识的限制，学生往往在解答过程中遇到很大的困难。如何在教学设计上增加学生感兴趣的知识点，使学生学习更积极主动，是重积分教学中教师着重考虑的内容。我们曾试图拉长教学时间，增加习题课时，这起到了一定的效果，能够帮助一部分学生理解。但是这次通过和学生的专业课内容相结合，让学生去探讨去发现，显然收效更好。这也使我们作为教育者更加理解了“因材施教”的意义。通过该问题的分析和讲解，学生一方面加深了对曲面积分的理解，对于曲面积分向各个平面投影会遇到的困难和如何选取最优解法有了进一步的认识；另一方面，学生一直理解学微积分是为了后续专业课的相关计算做基础，但是通过这次课程，学生发现，专业课学到的知识同样也可以用到微积分的学习中，帮助他们去求解相关习题，这也使得学生理解了学科之间相辅相成的关系。

四、教学能力的提升

数学的学习，对于工科的学生非常重要，但是学生往往不知道所学的专业知识如何来辅助学习高等数学。在上述问题的分析过程中，学生对高等数学的学习有了极大的热情，利用相关的工程制图知识，提高了高等数学相关知识的学习高度。这也是高等院校中多学科交叉融合的一个非常好的实例，让学生学以致用，在日常的学习中提升个人的学习能力。在这节课之后，我们和学生讨论了他们学习的工程制图课程所学习的内容，请学生来帮助我们做教学准备，看有哪些地方是可以和他们所学的专业课程相结合。这样既让学生有了自主学习的动力，在课堂上又达到了很好的教学效果，这一章结束的期中阶段性水平测验时，学生的解题能力都有了不同程度的提高。这也使得我们在教学设计时有了以下的经验总结，并做了相关的一些假设，准备加以实施，进一步地去学习和促进学科融合，让学生的数学学习有一些乐趣。

第一，切实做到因材施教，学生的专业不同，大多数的理工科学生都有高等数学、线性代数以及概率论与数理统计等几门数学课程，穿插在前两年的大学学习中去完成。对于不同专业的学生，我们想在下一步的教学中，适当增加与相关专业教师的交流。因为所学专业不同，不同学院之间的教师之间交流机会比较少，借助于相关数学课程的教学，增加和相关学院教师的交流机会，既能够了解到这些专业后续课程的学习需要哪些知识，又能做到因材施教，在这些内容上着重讲解，为后续课程的开展打好基础[4-5]。

第二，通过和学生以及相关教师的交流，探讨学科融合的一些契机，找到学科交叉的点，既是帮助学生学习水平的提高，也是我们科研交流的一个好的机会。从基础着手，增加自身的学识水平和专业知识，拓展专业内容，知识的碰撞总能擦出意想不到的火花，教学相长也为教师教学水平和科研能力的提升提供了好的平台。

第三，细化学生的学习内容，由于高等数学是理工科学生的必修课，市场上相关的辅导材料纷繁杂乱，学生做起来没有头绪。根据我校学生的专业分布，我们准备在教学过程中去寻找适合相关专业学生学习的习题，结合学生的专业特色以及招收水平，编纂对应难度的习题，辅助学生及时复习。我们准备组建教学组，进行分工，集合专业教师的能力，去推动这项工作的进行，通过实践实时反馈不断改进。如果这项工作能够做到相对满意的结果，对学生的培养应该是大有益处的。

习近平总书记在党的二十大报告中指出，要建立全民终身学习的学习型社会，学习型大国。而终身学习是在更好地适应经济社会全面发展的基础上不断学习，不断进步。高等学校的教育更是如此，要做到与时俱进，教师要根据时代的进步，人民生活环境的不断改善来实时地提高自己的教学能力，提升自己的教学水平，不能一成不变，不可故步自封。与不同专业的人才之间的交流，以及网络资源的充分利用，都是实现终身学习的有效途径。而正如陶行知先生所说，只有好学，才是终身进步之保险，也是常青不老之保证。作为高校教师，我们只有保持终身学习，才能成为一名合格的新时代教育工作者，才能培养好社会主义的建设者和接班人。