用v-t图巧解传送带的痕迹等困难问题

朱孟亮

(江苏省六合高级中学,江苏 南京 211500)

传送带问题对于初学者来说是个难点,其中摩擦力方向及其突变是分析的关键.传送带中的相对位移、痕迹、热量等问题更让很多学生感到焦头烂额、无从下手.有时即使求解出来,其过程也冗长繁杂,需要学生要有较强分析问题能力和想象力.这些问题如果巧借v-t图,就会如借神力、迎刃而解.笔者以下面这道改编题为例来分析说明.

例1.如图1所示,倾角θ=37°的传动带以10 m/s的恒定速率沿逆时针方向运行,传送带的上、下两端相距L=16 m.t=0时,将质量m=1 kg的物块(可视为质点)轻放在传送带上端,物块与传送带之间的动摩擦因数μ=0.5,以沿传送带向下为正,(设最大静摩擦力等于滑动摩擦力,g=10 m/s2,sin37°=0.6,cos37°=0.8).则以下说法正确的是

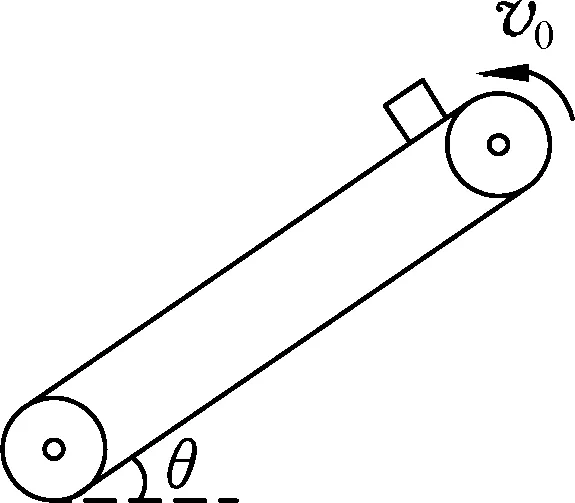
图1

(A) 物块相对于传送带的位移为6 m.

(B) 摩擦力对物块做的总功为24 J.

(C) 若物块为煤块,则在传送带上留下的痕迹为6 m.

(D) 物块在传送带上运动的过程中产生的热量为24 J.

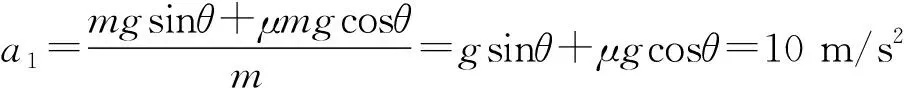
由上面的分析可见,该过程较为繁杂.如果借助v-t图,分析过程就既清晰又简单.以沿传送带向下为正,传送带和物块的v-t图如图2所示.另外还须注意以下几个原则: ① 在传送带和物块的v-t图线之间的面积即为物块相对于传送带的相对位移,而且在传送带v-t图线以下的面积为负(该段时间内物块相对于传送带的速度为负)、传送带v-t图线以上的面积为正(该段时间内物块相对于传送带的速度为正).② 全过程物块相对于传送带的位移为这些面积的代数和.③ 全过程物块相对于传送带的路程为这些面积的绝对值之和.④ 痕迹问题略微复杂一些,若两v-t图线之间的面积全在传送带v-t图线的一侧,则这些面积的绝对值之和即为痕迹长度.若两v-t图线之间的面积在传送带v-t图线的两侧且以某一时间点为分界,则面积的绝对值之和较大的那一侧面积的绝对值之和为痕迹长度.若两v-t图线之间的面积时而在传送带v-t图线以上、时而在传送带v-t图线以下,则要还原一下相对运动过程才能确定痕迹的长度.当物块受到人为外力F或传送速度变化时,以上规律仍然适用.

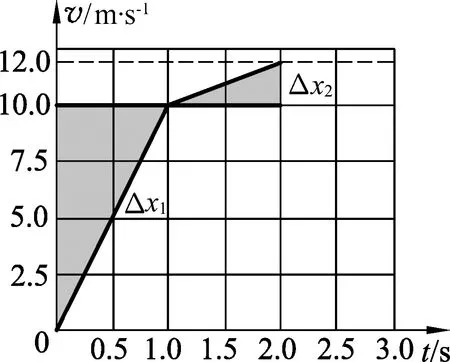
图2

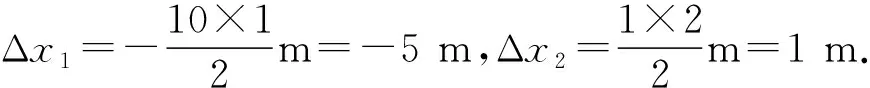
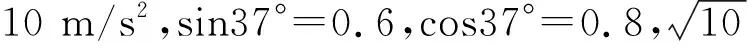
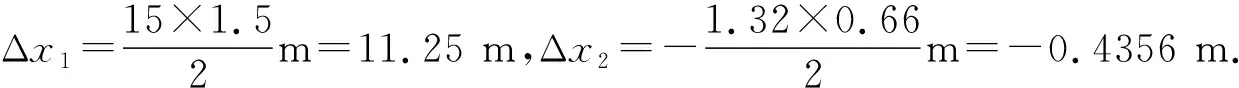
例3.一足够长的水平传送带左端放置质量为m=2 kg小煤块,煤块与传送带之间动摩擦因数为μ=0.2.现让传送带从静止开始以恒定的加速度a=4 m/s2顺时针匀加速运动,当其速度达到v=12 m/s时,立即以相同大小的加速度做匀减速运动直至静止.经过一段时间后,小煤块也静止了.求:(1) 煤块在传送带上留下痕迹的长度;(2) 整个过程中小煤块和传送带间因摩擦产生的热量.

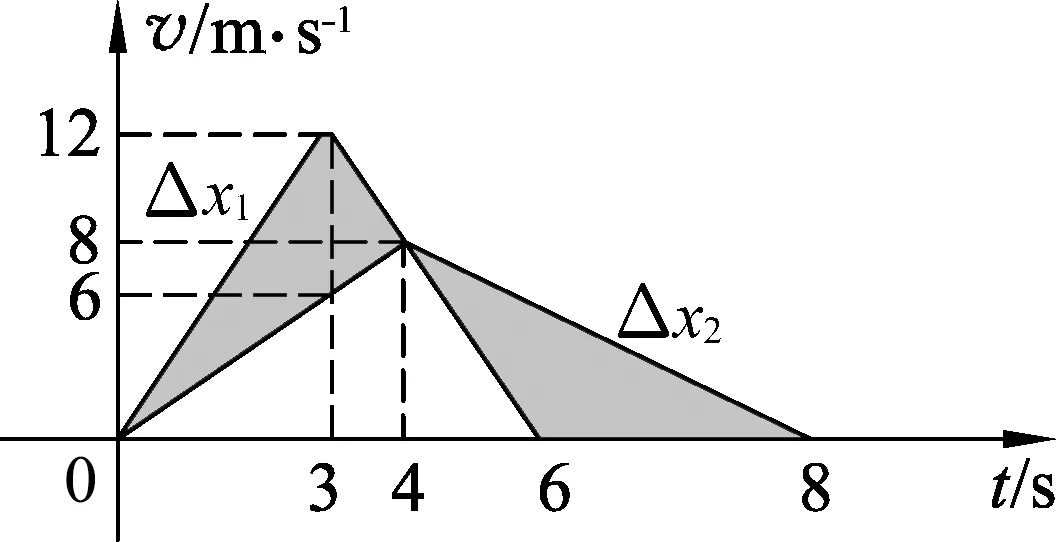
图4

例4.一与水平方向成θ=37°夹角、足够长的倾斜传送带以v0=2 m/s的恒定速率顺时针运行,质量为m=1 kg的小煤块(可视为质点)位于传送带底端,在沿传送带向上的拉力F=12 N作用下,煤块由静止开始向上运动,经过时间t0=1 s后,立即撤去拉力F.已知小煤块与传送带间的动摩擦因数μ=0.5,sin37°=0.6,cos37°=0.8,重力加速度g=10 m/s2.求煤块向上运动时在传送带上留下痕迹的长度.

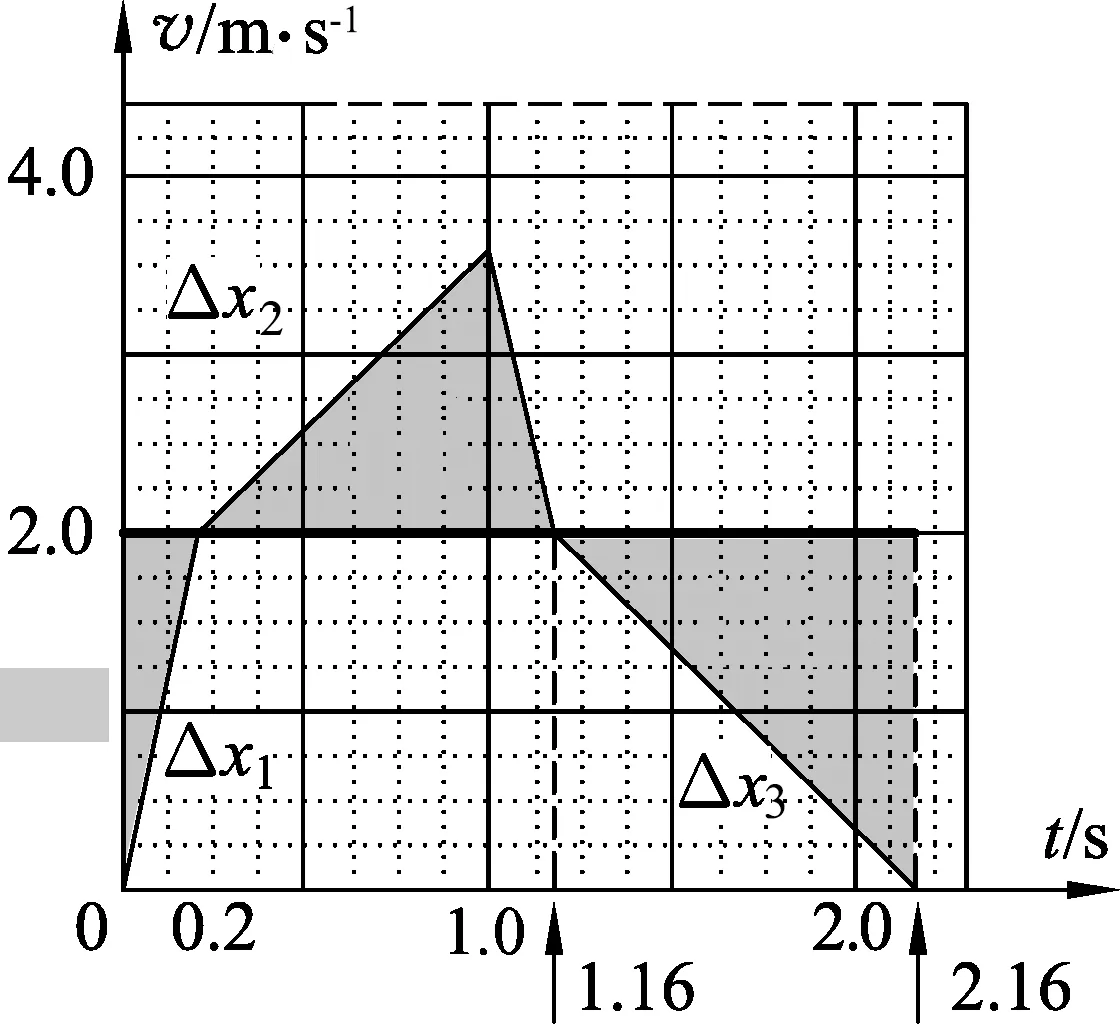
图5

由上面的几道题可见,此方法适用于所有的传送带物块问题,而且借助传送带和物块的v-t图,结合总结出的规律,传送带的相对位移、痕迹、热量等问题都可以轻松解决.当然受力分析和运动分析还是必须的,特别是传送带和物块运动转折点的速度和时间还是要求出来的,以便绘制v-t图和求面积.