一类忆阻型4D 保守混沌系统的设计及其分析

夏国莹,曾以成

(湘潭大学 物理与光电工程学院,湖南 湘潭 411105)

忆阻器是Chua[1]在1971 年首次提出的定义电荷和磁通量之间关系的基本元件。忆阻器具有非线性和非易失性,在人工神经网络[2-3]、逻辑运算[4]、人工智能[5-6]和图像加密[7]等诸多领域都有应用。其作为非线性元件,在混沌系统的构造中起着重要作用。到目前为止,学者们研究了一系列具有多涡卷、多翼、自激和隐藏吸引子现象的忆阻耗散混沌系统[8-10]。然而,对忆阻保守混沌系统的研究相对较少。

一般来说混沌系统可分为耗散系统和保守系统。如果系统散度也即系统雅可比矩阵(J)的迹tr(J)小于零,则为耗散系统,而如果tr(J)等于零,则系统为保守系统。特别地,有一个保守系统的tr(J)随时间变化的平均值为零[11]。因此,保守系统具有一些区别于耗散系统的特征,例如散度、相体积的时间变化率为零(或接近零)以及Lyapunov 指数之和为零。另一方面,根据哈密顿能量值,保守系统可以分为哈密顿系统和非哈密顿系统。如果一个保守系统的哈密顿能量变化率为零,则该系统为哈密顿保守系统;否则,为非哈密顿的保守系统。耗散系统产生的吸引子类型有极限环、汇以及混沌吸引子等,但保守混沌系统中没有吸引子,其运动轨迹统称为“流”[11],或称之为混沌海。与耗散系统相比,保守系统在图像加密等应用的安全性和抵抗攻击性方面更具有优势,是因为其没有吸引子和对初始条件极端敏感性的特殊性[12-13]。

因此,保守系统近年来受到了越来越多的关注。2018 年,Singh 和Roy[14]提出了五个具有保守自治性质和平衡点为非双曲平衡点的四维混沌系统,并用Lyapunov 指数谱、Poincaré 映射、分岔图等分析了其动力学特性。同年,Wu 等[15]提出了一个体积保守且具有非双曲不动点的五维光滑自治超混沌系统。2020年,Deng 等[16]提出了一种含有忆阻器和电容的三维保守混沌电路。该系统对初始值和参数高度灵敏,还有共存轨道和瞬态现象等特征。同年,Jia 等[17]基于Sprott-A 系统,通过能量的分析,提出一个四维具有共存隐藏吸引子的新哈密顿保守系统。2022 年,Du等[18]提出了一个基于忆阻的五维保守混沌系统,该系统具有多种准周期拓扑,并具有同态和异态的多稳态特性。对于上述提出的保守混沌系统简单列了一个表格,详细信息见表1。通过表1 可知,随着对保守混沌系统的研究深入,保守系统具有的丰富的动力学特性也大量被发现,但忆阻型保守混沌系统非常少。

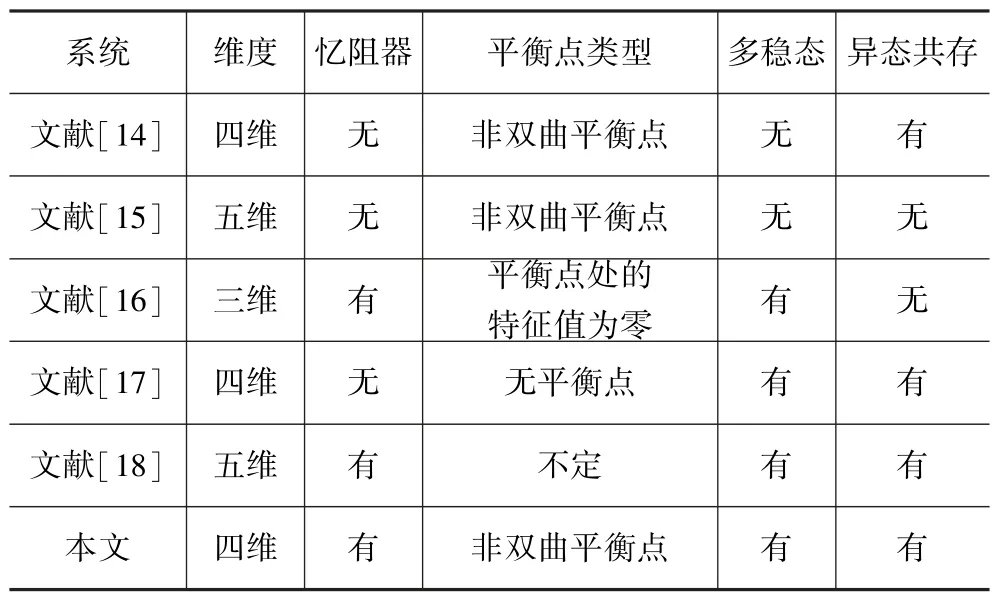
表1 不同的保守混沌系统Tab.1 Different conservative chaotic systems

本文提出一个忆阻型四维保守混沌系统,根据理论分析该系统为相体积守恒、能量不守恒的非哈密顿保守系统。系统具有多种准周期拓扑结构以及混沌流和准周期流共存等特性。根据系统方程,设计Multisim 仿真电路,验证该系统的可行性。

1 保守混沌系统构建及其分析

1.1 忆阻型系统模型

经典保守混沌Sprott-A 系统[19],其系统方程表达式如式(1)所示:

式中:x、y、z为状态变量。

在该系统中引入忆导M(u)=ku2+b的磁控忆阻器,系统方程可修改为:

这里为了得到复杂的动力学行为,修改系统状态方程组的第一个方程为=a(y-u),u为系统变量。其中,三阶磁控忆阻的表达式为:

式中:i为流过忆阻器的电流;v为忆阻器两端电压;φ为磁通量。

当令参数a=0.1,k=0.1,b=1,系统初始值为(0.1,0.1,0.1,0.1) 时,用ODE45 算法进行Matlab 仿真,系统的y-z,x-u,x-z平面和x-y-z空间的相轨图如图1 所示,从空间和不同平面的相轨图上可以看出复杂的拉伸和折叠。此时系统的Lyapunov指数分别为LE1=0.0382,LE2=0.0008,LE3=-0.0008,LE4=-0.0382,其中最大Lyapunov 指数大于0,系统处于混沌状态。其计算收敛过程曲线如图2(a)所示,Lyapunov 指数之和如图2(b)所示,可发现系统经过暂态后的Lyapunov 指数之和为0。

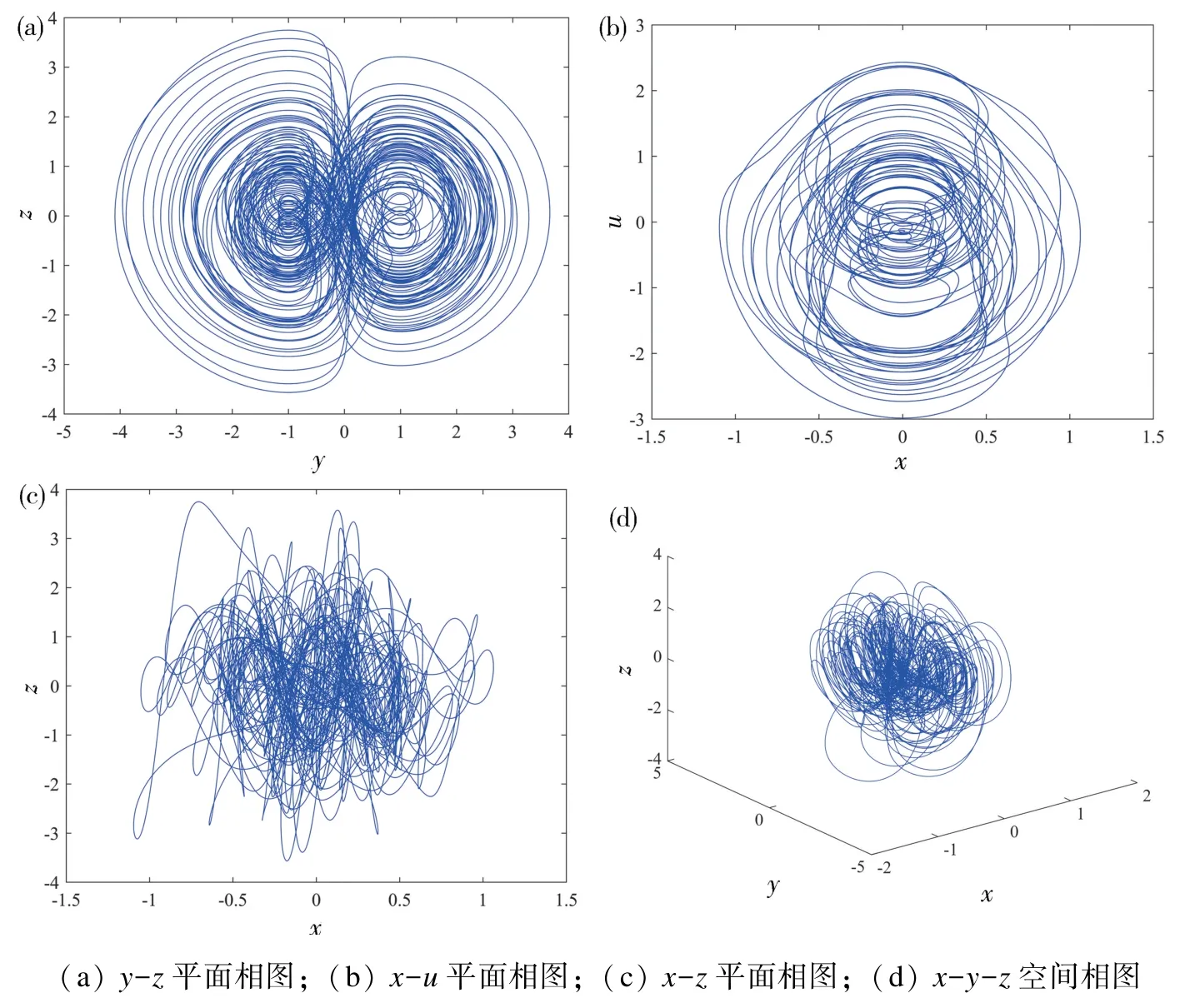
图1 系统混沌流相图Fig.1 Phase diagrams of the chaotic flow

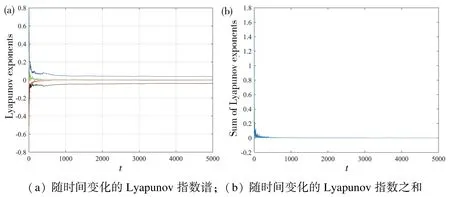
图2 系统Lyapunov 指数谱和Lyapunov 指数之和Fig.2 Lyapunov exponent spectra of system and sum of Lyapunov exponents

1.2 平衡点分析

根据平衡点计算的特征值如表2 所示。由表2 可知,计算得到的平衡点E1和E2的特征方程是一样的,其中A为二次项系数,A=ak+ab+2+a,因此特征值也是一样的。特征值实部为零,表明都为非双曲平衡点。

表2 平衡点雅可比矩阵特征值Tab.2 Characteristic value of equilibrium Jacobian matrix

1.3 对称性分析

对系统进行坐标变换(-x,-y,z,-u)↔(x,y,z,u),如式(5)所示。

可发现系统方程并未发生改变。因此,在空间中,系统(2)的每组解都围绕z轴对称。

1.4 保守性分析

该系统的散度计算如公式(6)所示,表明该系统的耗散性仅和z有关。如果z的平均值为零[20-21],则系统具有保守性。当参数a=0.1,k=0.1,b=1时,初始值为(0.1,0.1,0.1,0.1),系统散度随时间变化的平均值如图3 所示。从图3 可知,忽略瞬态部分,系统散度随时间变化的平均值为零。

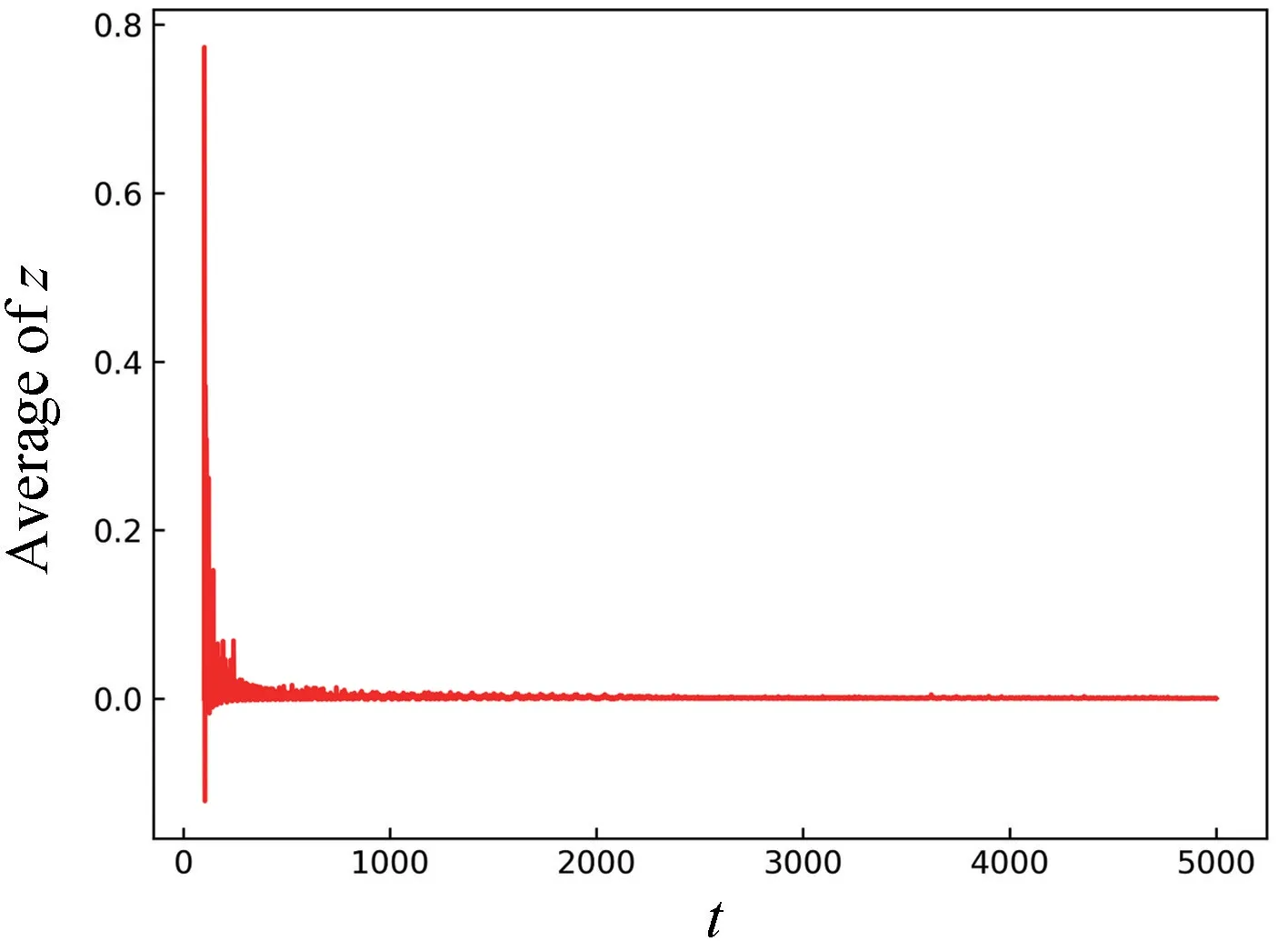
图3 随时间变化的z 的平均值Fig.3 The average of z varying with time

假设相空间中体积V(t)的任意闭合曲面为S(t)。设体积V(t)在经过无穷小时间dt的体积为V(t+dt),则相应的曲面面积为S(t+dt),则可得到:

式中:A和n分别表示曲面S的表面积和曲面上从内到外的单位法向量。式(7)也可写成如下表达式:

根据散度定理,可表示为式(9)。

其中(∇·F)即为F的散度,根据式(6)～(9)可得到:

从式(10)可以得到,z随时间变化的平均值为零(见图3),也即系统的空间相体积是恒定的,系统是体积保守的。

1.5 能量分析

1991 年,Arnol'd 等[22]提出用Kolmogorov 系统来描述耗散强迫动力系统或流体动力学的不稳定性。Kolmogorov 型变换可以判断系统的哈密顿能量是否保守[17]。Kolmogorov 型变换可描述为[17,23]:

式中:x∈Rn表示系统的状态变量;J(x)∈Rn·n表示反对称矩阵;H(x):Rn→R代表哈密顿能量;{x,H(x)} 对应于系统的能量保守部分;Δx对应系统的耗散部分;f为系统的外加能量。当方程(11)中没有Δx和f时,哈密顿能量是一个非零常数(哈密顿能量的变化率等于零),即哈密顿能量守恒系统;否则是非哈密顿系统。为了实现这种变换,系统(2)必须满足反对称条件[23]。因此,假设X=hx,Y=y,Z=z和U=mu,其中h和m是两个非零常数,系统(2)可写为式(12)的变换:

该系统的哈密顿能量部分为:

对式(15)进行计算,系统的哈密顿能量变化率为:

很明显该系统的哈密顿能量变化率不为零,即该系统为非哈密顿能量的体积保守混沌系统。

1.6 参数对系统动力学行为的影响

随着系统参数的变化,系统会处于不同的状态。固定初始值(0.1,0.1,0.1,0.1),当参数b=1,k=0.1 时,参数a在[0,10]范围内的Lyapunov 指数谱如图4(a)所示,状态变量y随参数a变化的分岔图如图4(c)所示。可以得到,参数a在区间[0,1.56],[2.04,2.48],[2.58,2.72],[2.83,3.07],[3.60,4.02]处于混沌状态,在区间[1.57,2.03],[2.49,2.57],[2.73,2.82],[3.08,3.59],[4.03,10]处于准周期状态。当参数a=0.1,k=0.1 时,参数b在[0,10]范围内的Lyapunov 指数谱如图4(b)所示,状态变量y随参数b变化的分岔图如图4(d)所示。可以得到,参数b在区间[0,1.48],[3.09,3.75]处于混沌状态,在区间[1.49,3.08],[3.76,10]处于准周期状态。系统随a、b参数变化的Lyapunov 指数之和分别如图4(e)和(f)所示。总的来说,系统(2)从混沌状态开始,随着a、b参数的变化,系统存在混沌状态和准周期状态的来回切换,最后稳定在准周期状态。Lyapunov 指数谱具有关于水平x轴对称的结构,系统的Lyapunov 指数之和为零。此外,分岔图与Lyapunov 指数谱也相对应。

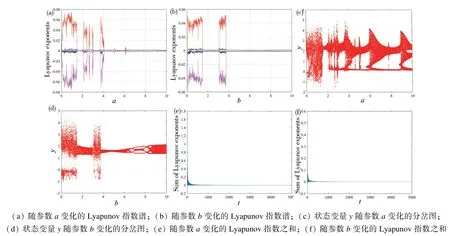
图4 系统随参数a、b 变化的Lyapunov 指数谱、分岔图以及Lyapunov 指数之和Fig.4 Lyapunov exponent spectra,bifurcation diagrams and sum of Lyapunov exponent of the system varying with a, b

参数a、k和初始值同上,b取值准周期状态区间,随b值的变化,系统(2)具有丰富的准周期拓扑结构。b取不同值时,x-z平面准周期相轨图如图5 所示。

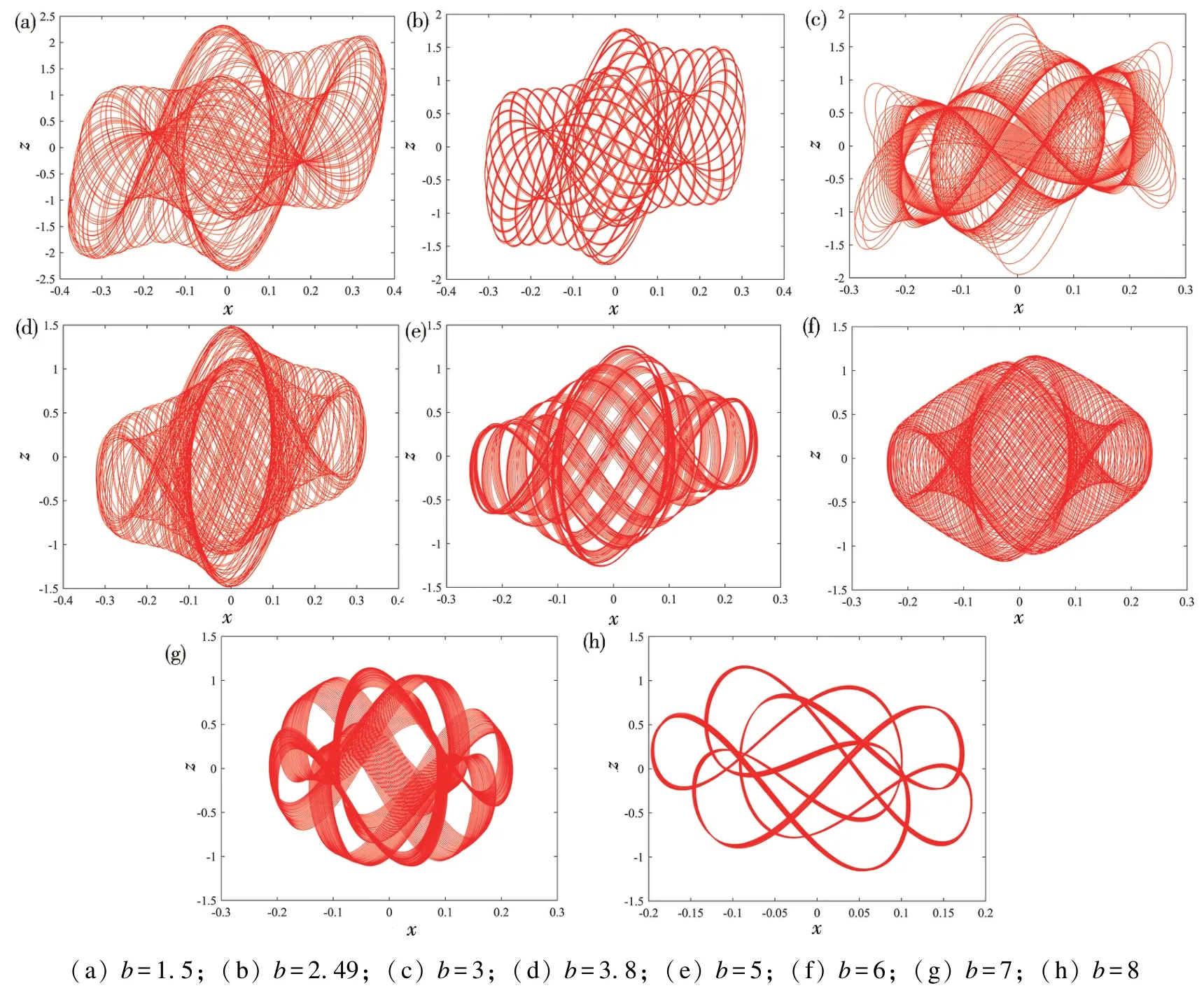
图5 b 取不同值的准周期拓扑相轨图Fig.5 Quasi-periodic topological phase diagrams with b in different values

从图4(b)中可以得到,当b=1 时为混沌状态,b=10 时为准周期状态。固定参数a=0.1,k=0.1,初始值(0.1,0.1,0.1,0.1),当b=1 时,y-z,xz,z-u平面的混沌流相图(青绿色)如图6(a),(c),(e)所示;当b=10 时,对应平面的准周期流相图(青绿色)如图6(b),(d),(f)。红点则显示了图6 中yz,x-z,z-u各个切面上对应的Poincaré 映射。根据系统不同平面上的Poincaré 映射,可得到验证: 准周期的Poincaré 映射是一条闭合曲线或只有有限个点,而混沌的Poincaré 映射是一些离散点。

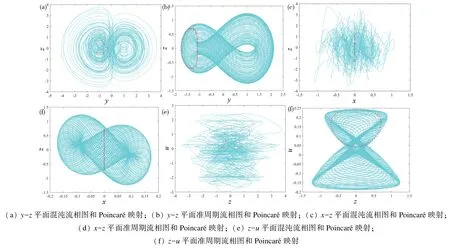
图6 系统混沌流和准周期流相图及其Poincaré 映射Fig.6 Phase diagrams of the chaotic flows and quasi-periodic flows and their Poincaré map

1.7 初始值对系统动力学的影响

当系统参数不变时,不同初始值可能会产生具有多个不同拓扑结构的吸引子(保守系统的混沌流或准周期流)称为多稳态。系统(2)对初始值变化敏感,受初始值影响,可产生混沌流和准周期流的状态切换。参数a=0.1,k=0.1,b=1 保持不变时,设初始值为(0.1,y(0),0.1,0.1) 或(0.1,0.1,z(0),0.1)。关于初始值y(0)和z(0)的Lyapunov 指数谱和相应分岔图如图7 所示。从图7 可知,所有Lyapunov指数谱也关于水平x轴对称。根据图7(a),当y(0)在区间[-5,-1.3],[-0.64,0.5]和[1.52,5]系统处于混沌状态,当y(0) 在区间[-1.29,-0.65],[0.51,1.51]系统处于准周期状态。从图7(c)可得z(0)取值[-5,5],系统始终处于混沌状态。

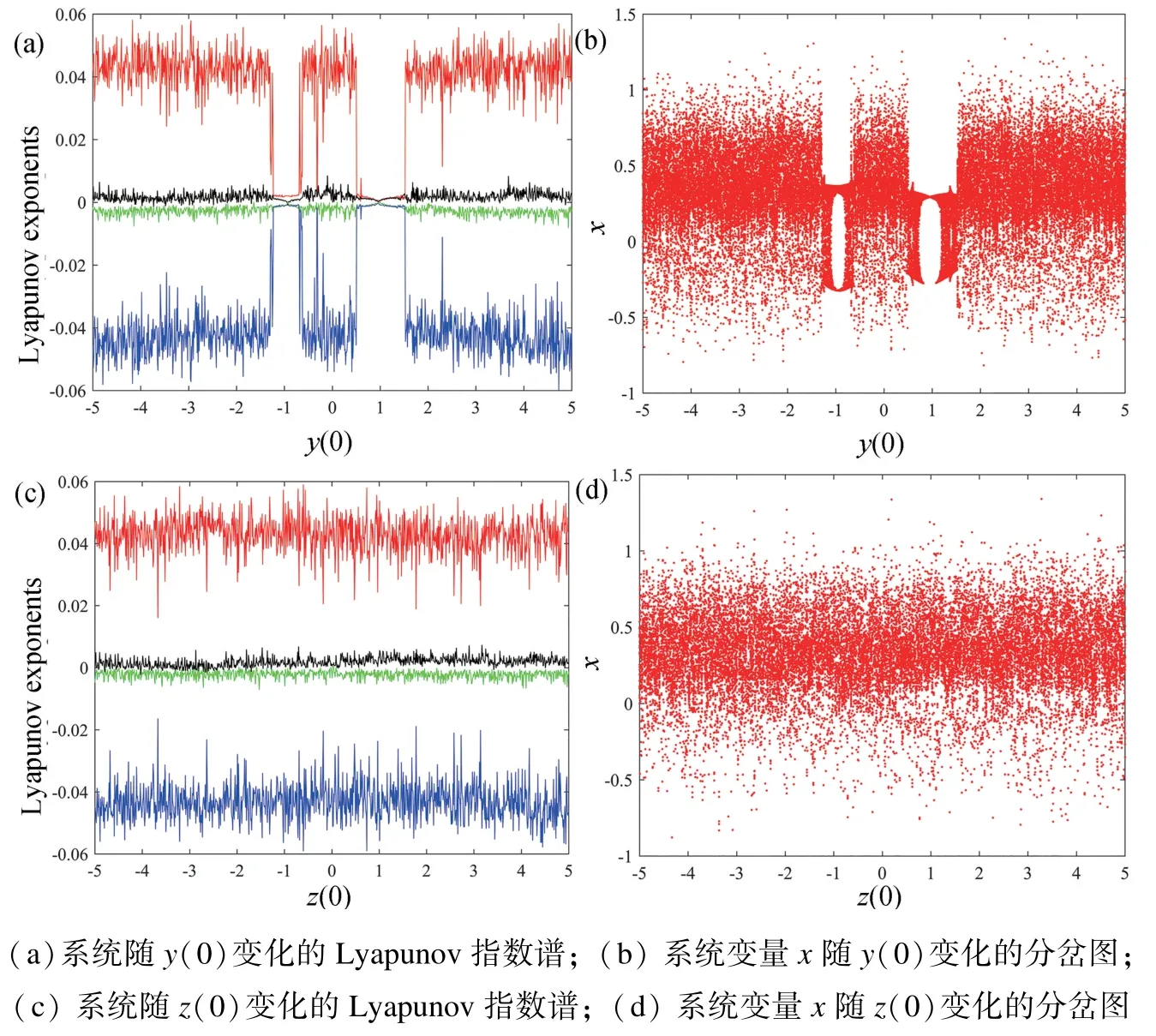
图7 系统随初始值y(0)、 z(0)变化的Lyapunov 指数谱和分岔图Fig.7 Lyapunov exponent spectra and bifurcation diagrams of the system varying with initial values y(0), z(0)

1.8 共存现象

固定参数值时,系统(2)可以由不同的初始值产生无穷多个共存流。有趣的是,对于不同的初始值,该系统可产生混沌流和不同幅度周期流的非对称共存。选取参数a=0.1,k=0.1,b=1 不变,如图8(a)所示,可产生初始值为(0.1,0.01,0.1,0.1)的混沌流(蓝色),(0.1,0.05,0.1,0.1)的混沌流(红色),(0.1,0.8,0.1,0.1)的周期流(青绿色),(0.1,1,0.1,0.1)的周期流(玫红色)共存现象。此外,固定参数a=0.1,k=0.1,b=10,改变系统初始值,还可得到准周期共存流,如图8(b)所示,初始值分别为(0.1,0.1,0.1,0.1) (红色),(-0.1,-0.1,0.1,-0.1)(蓝色),(0.1,0.1,0.1,-0.1)(青绿色)的准周期流共存现象。

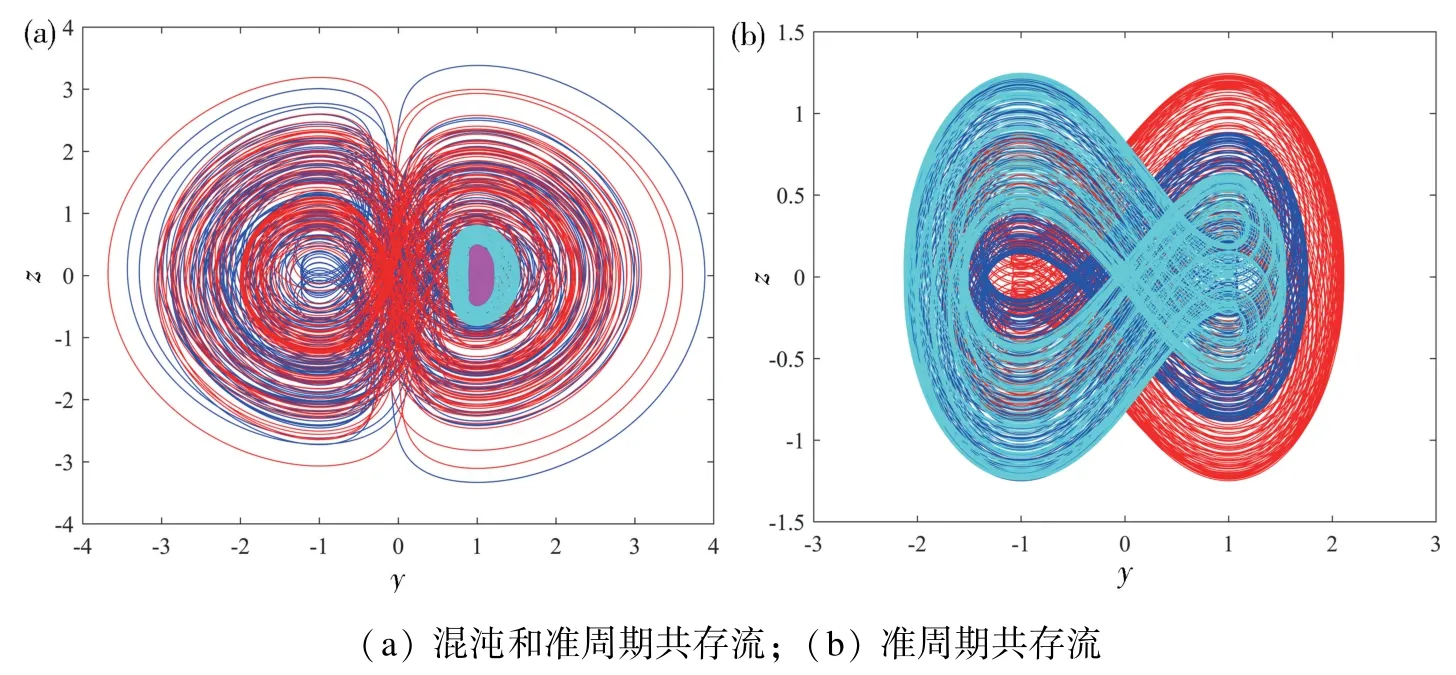
图8 系统在不同初始值下的共存现象Fig.8 Coexistence of the system with different initial values

2 电路实现

本部分根据系统状态方程和电路理论设计系统(2)的等效模拟电路。选取参数a=0.1,k=0.1,b=1 设计系统电路,对系统的状态方程进行时间尺度变换,令t=δτ,δ为时间尺度变换因子,取δ=1000,如式(17)所示:

根据式(17)所设计系统的电路原理图如图9 所示,相应的电路方程为式(18)所示。

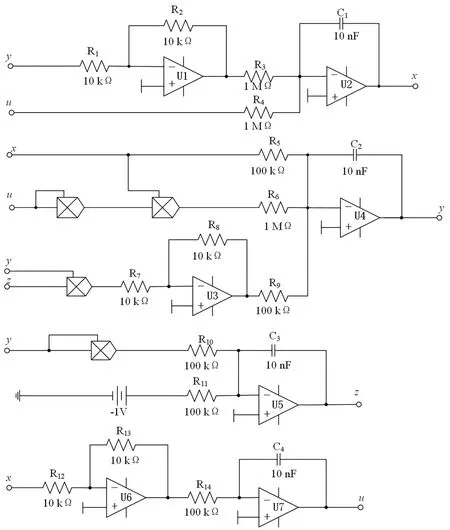
图9 系统Multisim 仿真电路Fig.9 Multisim emulator circuit of the system

该电路采用线性电阻、电容、运算放大器、模拟乘法器等电路元件。其中,运算放大器所选择的工作电压为±15 V。计算所得的电容、电阻值如图9 所示。Multisim 电路仿真结果如图10 所示,与Matlab 的数值仿真结果对比,整体上是一致的,其结果验证了理论分析的正确性。

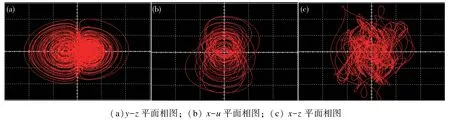
图10 Multisim 仿真相轨图Fig.10 Phase diagrams by Multisim software simulation

3 结论

本文提出一类基于忆阻器的四维保守混沌系统,通过计算系统散度和对其进行Kolmogorov 型变换分析了它的保守性,该系统散度随时间变化的平均值为零,哈密顿能量变化率不为零,因此为相体积守恒、哈密顿能量不守恒的保守混沌系统。分析了系统随参数和初始值变化的Lyapunov 指数谱和分岔图,发现其具有Lyapunov 指数之和为零、Lyapunov 指数谱关于水平x轴对称等特征;还具有多种准周期拓扑结构,同态和异态共存的多稳态特性。最后,通过模拟电路实验验证了相关的理论分析的正确性。保守系统比耗散系统在图像加密方面的应用更具优势,该保守系统的提出为混沌在图像加密方面的应用提供性能优良的备选系统。