动力学中的临界极值问题的解题策略

黄宽宽

(湖北省孝感市第一高级中学)

在物体运动状态发生变化的过程中,往往达到某个特定状态时,有关的物理量将发生突变,此状态叫作临界状态,相应物理量的值叫作临界值。临界状态的两侧,物体的受力情况、变化规律、运动状态一般都要发生改变,用变化的观点正确分析其运动规律是求解这类题目的关键,而临界状态的确定是求解这类题目的基础。

一、题型特点

(一)当物体的运动从一种状态转变为另一种状态时必须有一个转折点,这个转折点所对应的状态叫作临界状态;在临界状态时必须满足的条件叫作临界条件。

(二)临界或极值条件的标志

1.题目中有“刚好” “恰好” “正好”等字眼,表明题述的过程存在着临界点;

2.若题目中有“取值范围” “多长时间” “多大距离”等词语,表明题述的过程存在着“起止点”,而这些起止点往往对应的就是临界状态;

3.若题目中有“最大” “最小” “至多” “至少”等字眼,表明题述的过程存在着极值,这个极值点往往是临界点。

二、解题思路

(一)分析流程

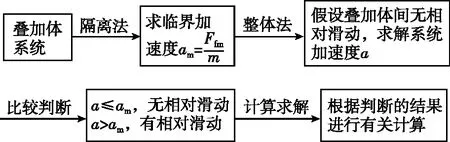
(二)涉及问题

1.接触与脱离的临界条件：两物体相接触或脱离,临界条件是弹力FN=0。

2.相对滑动的临界条件：两物体相接触且处于相对静止时,常存在着静摩擦力,则相对滑动的临界条件是静摩擦力达到最大值。

3.绳子断裂与松弛的临界条件：绳子所能承受的张力是有限的,绳子断与不断的临界条件是绳中张力等于它所能承受的最大张力,绳子松弛的临界条件是FT=0。

4.加速度最大与速度最大的临界条件：当物体在受到变化的外力作用下运动时,其加速度和速度都会不断变化,当所受合外力最大时,具有最大加速度;合外力最小时,具有最小加速度。当加速度等于零时,往往会出现速度最大或速度最小的情形。

三、常见模型

(一)接触物体分离的临界条件是弹力FN=0

【例1】如图1所示,在倾角α=30°的光滑斜面上,并排放着质量分别为mA=10 kg和mB=2 kg的A、B两物块。一劲度系数k=400 N/m的轻弹簧一端与B相连,另一端与固定挡板相连,整个系统处于静止状态。现对A施加一沿斜面向上的力F,使A沿斜面向上做匀加速运动。已知力F在前0.2 s内为变力,0.2 s后为恒力,g取10 m/s2。求力F的最大值和最小值。

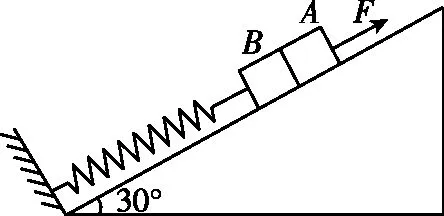
图1

解：因为在t=0.2 s内F是变力,在t=0.2 s 以后F是恒力,所以在t=0.2 s时,A与B开始分离,此时A与B间的作用力FN为零。设在0～0.2 s 时间内A与B沿斜面向上运动的距离为x,对A,根据牛顿第二定律可得

F+FN-mAgsinα=mAa

对A和B整体应用牛顿第二定律可得

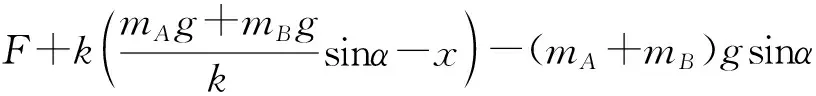
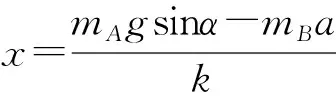
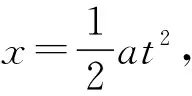
【点评】从受力角度看,两物体分离的条件是两物体间的正压力为0。从运动学角度看,一起运动的两物体恰好分离时,两物体在沿斜面方向上的加速度和速度仍相等。先根据平衡条件求出弹簧开始的压缩量,因为在前0.2 s时间内,F为变力,0.2 s 以后,F为恒力,所以在0.2 s时,A、B分离,B对A的作用力为0,对物体B运用牛顿第二定律列式得出F与加速度的关系式,当A、B开始运动时拉力最小,当A、B分离时拉力最大,根据牛顿第二定律即可求解。

【变式训练1】如图2所示,A、B两个物体靠在一起,静止在光滑的水平面上,它们的质量分别为mA=1 kg、mB=3 kg,现用水平力FA推A,用水平力FB拉B,FA和FB随时间t变化的关系如图3所示,则 ( )

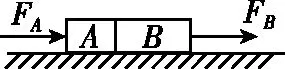
图2

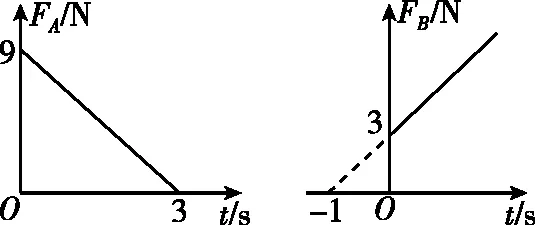
图3

A.A、B分开之前,A物体所受的合外力逐渐减小

B.t=3 s时,A、B脱离

C.A、B分开前,它们一起运动的位移为6 m

D.A、B分开后,A做减速运动,B做加速运动

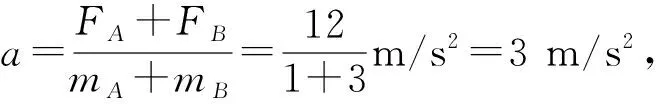
【点评】本题考查图像与临界问题的综合应用。在未脱离的过程中,整体受力向右,且大小恒定为FA+FB=12 N,根据牛顿第二定律求出加速度,脱离时满足A、B加速度相同,且弹力为零,根据牛顿第二定律列式求得时间,运动位移根据匀加速直线运动位移时间公式求解。

(二)绳子松弛的临界条件是绳中张力FT=0

【例2】如图4所示,当斜面以多大加速度a向左运动时,小球沿斜面上移?

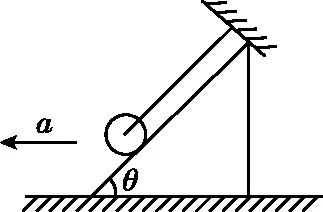
图4

【解析】当绳的拉力为零时,小球受力如图5。由牛顿第二定律得F合=mgtanθ=ma0,a0=gtanθ,即当a>a0=gtanθ时,小球沿斜面上移。

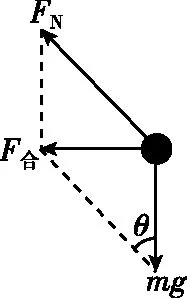
图5

【点评】斜面静止时,小球受重力、弹力和拉力而静止。当小球随斜面向左加速运动,则绳的拉力将减小,支持力增大,以获得水平向左的加速度,加速度足够大时,小球可能沿斜面上移,因此绳的拉力为零是球上移的临界条件。

【变式训练2】如图6所示,沿水平面运动的小车里,用两根轻质细线A、B悬挂一个小球,小车光滑底板上有一个用轻质弹簧拴着的物块,已知两根悬线与竖直方向夹角均为θ=30°,弹簧处于拉伸状态,小球和物块质量均为m,均相对小车静止,重力加速度为g,下列说法正确的是 ( )

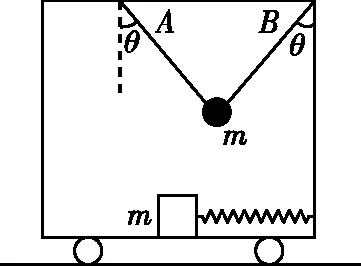
图6

A.小车一定水平向右做匀加速运动

B.两根轻细线的拉力都不可能为0

C.两根细线的拉力有可能相等

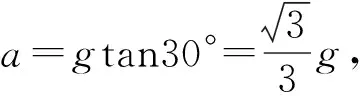
【点评】考查对不同研究对象的受力分析,掌握牛顿第二定律与力的合成与分解的应用,注意相对静止是解题的关键。根据物块受力分析,从而确定运动情况;对小球进行受力分析,依据牛顿第二定律,从而确定细线A是否有力;由牛顿第二定律,依据加速度不同,从而确定细线B的拉力可能值;根据力的合成与分解,依据平衡条件,及牛顿第二定律与胡克定律,即可求解。

(三)叠加体系统中恰好要发生相对滑动时,其静摩擦力达到最大值,即F静=Ffm

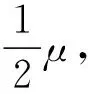
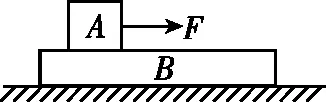
图7

A.当F<2μmg时,A、B都相对地面静止

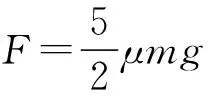
C.当F>3μmg时,A相对B滑动

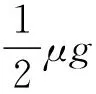
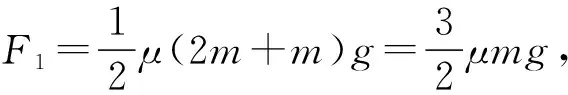
【点评】当F大于地面对B的最大静摩擦,且力F较小时,加速度较小,B对A的摩擦力也小,A、B一起运动。随着力F增大,加速度a增大,B对A的摩擦力增大,最大静摩擦力是极限。则A、B发生相对运动的临界条件是两者之间的摩擦力为最大静摩擦力。

(四)极值问题

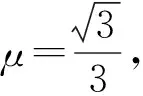
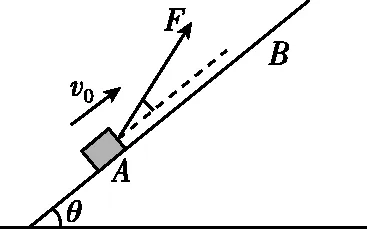
图8

(1)求物块加速度的大小及到达B点时速度的大小。

(2)拉力F与斜面夹角多大时,拉力F最小?拉力F的最小值是多少?

解：(1)由运动学方程得

代入数值解得a=3 m/s2,vB=8 m/s

(2)对物块受力分析,如图9所示,设拉力F与斜面成α角,在垂直斜面方向,根据平衡条件可得Fsinα+FN=mgcos30°,沿斜面方向,由牛顿第二定律可得Fcosα-mgsin30°-Ff=ma

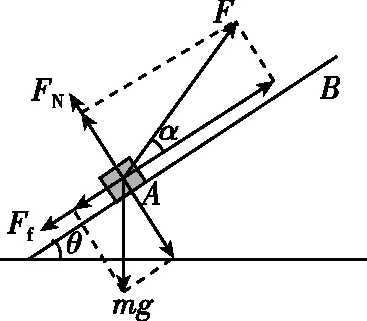
图9

又Ff=μFN

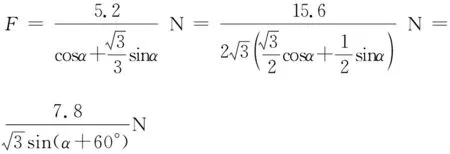
【点评】本题考查牛顿第二定律,是已知运动情况确定受力情况,先根据运动学公式求解加速度,然后根据牛顿第二定律列式讨论,求解出拉力F的表达式,分析出最小值,利用数学知识求解极值问题是解题关键。

四、高考命题角度

滑块—木板模型是力学中最常见的模型之一,是历年高考的热点内容。该类试题有如下几种命题角度。

(一)物块不受力而木板受拉力

木板受逐渐增大的拉力而物块不受力,这种情况下,开始物块和木板一起做加速运动,当物块加速度达到其最大值μg时,物块、木板开始发生相对运动,此后物块加速度保持不变,木板加速度逐渐增大。

(二)物块有初速度,两者都不受拉力且叠放在光滑水平面上

1.若木板足够长,这种情况下,物块减速、木板加速,直至两者速度相等将一起做匀速运动,其速度关系为v0-a块t=a板t。

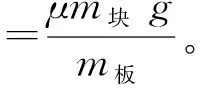
(三)木板有初速度,两者都不受拉力且叠放在光滑水平面上

1.若木板足够长,木板减速物块加速,直至两者速度相等将一起匀速运动下去,其速度关系为v0-a板t=a块t。

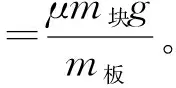
【真题再现】(2015·全国Ⅰ卷新课标·25)一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5 m,如图10所示。t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1 s时木板与墙壁碰撞(碰撞时间极短)。碰撞前后木板速度大小不变,方向相反,运动过程中小物块始终未离开木板。已知碰撞后1 s时间内小物块的v-t图线如图11所示。木板的质量是小物块质量的15倍,重力加速度大小g取10 m/s2。求：

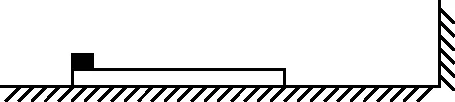
图10

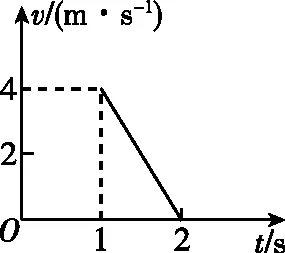
图11

(1)木板与地面间的动摩擦因数μ1及小物块与木板间的动摩擦因数μ2;

(2)木板的最小长度;

(3)木板右端离墙壁的最终距离。

解：(1)规定向右为正方向。木板与墙壁相碰前,小物块和木板一起向右做匀变速运动,设加速度为a1,小物块和木板的质量分别为m和M。由牛顿第二定律有

-μ1(m+M)g=(m+M)a1

①

由题图11可知,木板与墙壁碰前瞬间的速度v1=4 m/s,由运动学公式有

v1=v0+a1t1

②

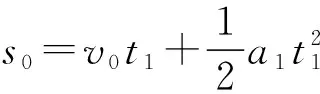
③

式中t1=1 s,s0=4.5 m是木板碰前的位移,v0是小物块和木板开始运动时的速度

解得μ1=0.1

④

在木板与墙壁碰撞后,木板以-v1的初速度向左做匀变速运动,小物块以v1的初速度向右做匀变速运动。设小物块的加速度为a2,由牛顿第二定律有-μ2mg=ma2

⑤

⑥

式中t2=2 s,v2=0

解得μ2=0.4

⑦

(2)设碰撞后木板的加速度为a3,经过时间Δt,木板和小物块刚好具有共同速度v3。由牛顿第二定律及运动学公式得

μ2mg+μ1(M+m)g=Ma3

⑧

v3=-v1+a3Δt

⑨

v3=v1+a2Δt

⑩

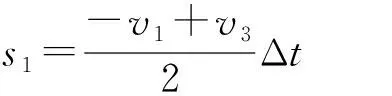
小物块相对木板的位移为Δs=s2-s1

解得Δs=6.0 m

因为运动过程中小物块没有脱离木板,所以木板的最小长度应为6.0 m

(3)在小物块和木板具有共同速度后,两者向左做匀变速运动直至停止,设加速度为a4,此过程中小物块和木板运动的位移为s3。由牛顿第二定律及运动学公式得

μ1(m+M)g=(m+M)a4

碰后木板运动的位移s=s1+s3

解得s=-6.5 m,木板右端离墙壁的最终距离为6.5 m

【点评】本题可以用常规方法分析,亦可以渗入匀变速直线运动的多种技巧与方法求解,体现命题者高超的命题技能。本题突出体现物理模型和物理方法是物理学的重要内容,也是高考突出考查的重点。所以在备考的过程中,考生只要掌握足够的重点物理模型、物理解题常见的技巧与方法,就可以举一反三,不用进行可怕的题海战术也能得到理想的分数。

五、结束语