“小题大做”中的学科素养与关键能力
李振涛 王淑玲
(北京市顺义牛栏山第一中学)
2022年高考全国卷体现了鲜明时代主题,强化对学生的价值引领并引导学生全面发展.高考试题坚持通性通法在解题中的运用,同时重视对核心素养的考查,题目形式较灵活,这也有利于引导中学教学回归正常轨道,避免一味练习传统的难题怪题.下面笔者通过2022年两道高考选择题的多角度解析,梳理出比较两个数的大小常用的方法和基本原理,剖析了命题者的目的,从考查学生的学科素养和关键能力的方式方法上进行了分析,并给出了教学建议.
1.题目与求解
【例1】(2022·全国甲卷文·12)已知9m=10,a=10m-11,b=8m-9,则
( )
A.a>0>bB.a>b>0
C.b>a>0 D.b>0>a
【解题思路】

【点评】根据指对互化以及对数函数的单调性可知m=log910>1,再利用基本不等式、换底公式可得m>lg11,log89>m,然后由指数函数的单调性即可解出.

因为a=10m-11=10m-10lg11,
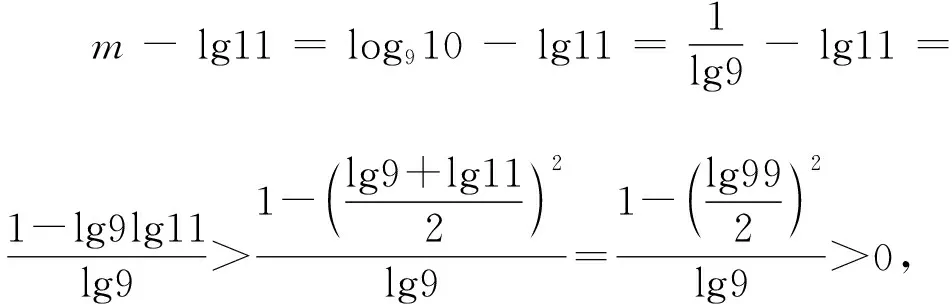
所以a=10m-10lg11>0.
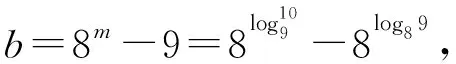
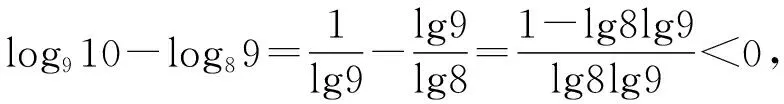
综上,a>0>b,故选A.
【点评】通过对数恒等式,将问题转化为同底数幂的运算问题.利用基本不等式进行放缩解决问题.

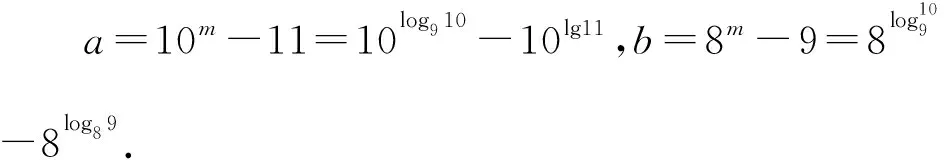

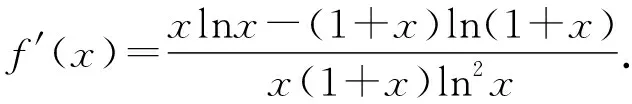
令h(x)=xlnx-(x+1)ln(x+1),x>1,
则h′(x)=lnx-ln(x+1)<0,
所以h(x) 所以f′(x)<0,所以f(x)单调递减, 所以log89>log910>log1011, 所以a=10m-11>10lg11-10lg11=0, 【点评】此方法中关注了幂的变化规律,从而构造出函数f(x),利用函数的单调性解决问题. 解法四:由9m=10,所以a=10m-11=10m-10-1=10m-9m-1, b=8m-9=8m-10+1=8m-9m+1. 令f(x)=(t+1)x-tx(t>1,x>1), 则f′(x)=(t+1)xln(t+1)-txlnt>0, 所以f(x)单调递增,所以f(x)>f(1)=1, 则a=10m-11>10lg11-11=0, b=8m-9<8log89-9=0. 综上,a>0>b,故选A. 【点评】此方法中关注了底的变化规律,从而构造出函数f(x),利用函数的单调性解决问题. 综上,a>0>b,故选A. 【点评】此方法中关注了条件和结论间的关系,利用指数函数的单调性解决问题. ( ) A.a C.c 总体思路一:构造函数法 比较两个数的大小常用方法是构造函数,利用函数的单调性比较大小.构造函数的基本思路是根据两个数的结构特点,联想到相关知识从而构造出适合自身知识结构的函数,进而解决问题.构造出的函数形式因人而异,形式多变,体现出对基础知识的综合应用能力,也是创新思维的具体表现. 对于a,b的大小比较方法主要有下面的解法: 所以设f(x)=ln(1+x)-x(x>-1), 当x∈(-1,0)时,f′(x)>0,当x∈(0,+∞)时,f′(x)<0, 所以函数f(x)=ln(1+x)-x在(0,+∞)上单调递减,在(-1,0)上单调递增, 故a 令u(x)=(x-x2)ex-x(0 则u′(x)=(1-x-x2)ex-1, 令t(x)=(1-x-x2)ex-1(0 则t′(x)=(-3x-x2)ex, 因为0 所以u′(x)<0,所以u(x) 解法三:由题得lna-lnb=0.1+ln(1-0.1), 令f(x)=x+ln(1-x)(0 所以f(0.1) 对于a,c的大小比较方法主要有下面的方法: 由于a-c=0.1e0.1+ln(1-0.1), 令h(x)=ex(x2-1)+1,h′(x)=ex(x2+2x-1), 当0 所以当0 所以当0 所以g(0.1)>g(0)=0,即0.1e0.1>-ln0.9,所以a>c,故c 总体思路二:利用近似计算 近似计算是数据处理常用的方法,以直代曲是微积分的精髓,也是进行近似计算的常用方法.通过切线进行近似是中学中常用的近似方法. 解法一:ex在(0,1)的切线方程是y=1+x,所以ex≈1+x, ln(1+x)在点(0,0)处的切线是y=x,所以ln(1+x)≈x, c=-ln0.9=-ln[1+(-0.1)]≈-(-0.1)=0.1, 所以c 所以c 基本思路三:放缩法 放缩法是常用的数学方法,在解决各类数学问题中经常用到,其理论基础是不等式的传递性,因此可以把要比较的两个数进行适当的放大或缩小,使复杂的问题得以简化,来达到比较两个实数的大小的目的. 因为ex>1+x(0 所以a>0.11,所以a>c. 综上,c 我们可以看到,以上两个题目分别以学生熟悉的指对运算为背景,从学生非常熟悉的知识出发,考查学生比较数的大小的常用方法.学生可以通过构造函数,利用导数判断所构造函数的单调性,从而判断数的大小关系,也可以通过放缩法,或估值法对数据进行处理,最终得到数据的大小关系.题目可以很好的考查学生的逻辑推理能力、运算求解能力和数据处理能力.从思想方法的角度看,可以很好的考查函数与方程思想、化归与转化思想,以及数据估算与近似估计的思想.体现数学运算、逻辑推理和数据处理核心素养,从而考查学生的关键能力以及必备知识的掌握程度. 数的大小比较问题是高考中经常出现的题型,题目的背景灵活多变,可以在多个知识点设置题目,综合性强,灵活度高,并且难度比较好控制.今年这两道比较大小的问题解题方法灵活多变,综合性强,有效地规避了经常用的特殊值法,达到了去模式化、套路化的目标.试题设计的非常新颖,不仅有高度,还有深度,充分体现创新性,有效地规避解题的套路化,回归数学本质.用学生熟悉的知识背景,设计开放、灵活的题目,考查学生对学科内涵的理解广度与深度,从而考查学生的数学素养,更好的服务创新型人才的选拔. 比较两个数的大小是教材当中贯穿教学的一条内在主线,从预备知识开始就进行比较两个数的大小的基本方法.从基本事实:a,b∈R,a>b,a-b>0;a=b,a-b=0;a 《课程标准》、《中国高考评价体系》和《中国高考评价体系说明》是备考与命题的纲领性文件,结合高考试题,仔细研究这些文件在高考试题中是如何与四基四能相结合,怎样通过创新题目设置方式和背景,从而考查学生的关键能力与核心素养,教师在备课时把这些研究透彻后,就可以很好的把握命题方向,在复习时实现事半功倍的效果.教师要转变自身的教育理念,聚焦于核心素养,在《课程标准》和《中国高考评价体系》的指引下重塑知识间的关系,以核心素养和关键能力重新审视高中知识和方法,从而转变对于学生的培养方案和教学模式.使教师不仅仅是知识和方法的传授者,更应该是学生学习思想和方法的引领者. 教师可以对同一个问题创设不同的情境,采用不同的表述方式,多角度,多层次的考查学生的学科素养,学生在解题基本活动经验的积累过程中,根据各类试题的特点,归纳总结出解决某类问题的基本思路与方法,从而提炼通性、通法,如函数与方程、分类讨论、数形结合、化归与转化的思想,利于提升学生的学科核心素养.





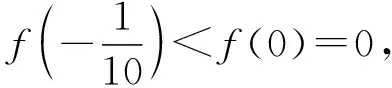




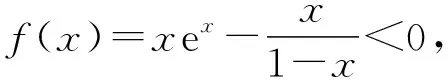
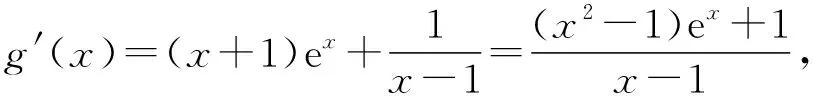
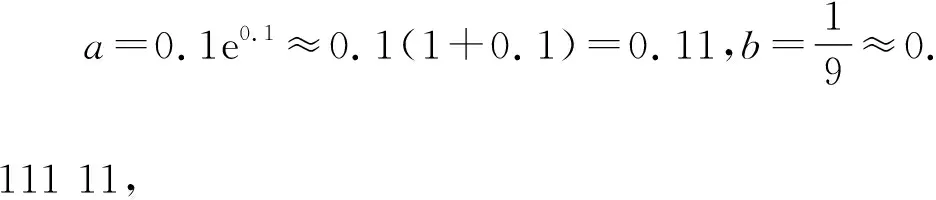


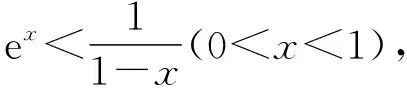
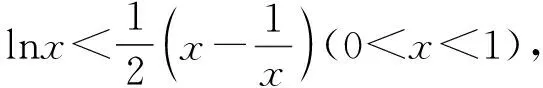

2.命题意图与试题评析
2.1 命题意图
2.2 试题评析
3.探本溯源
4.教学建议
4.1 立足必备知识 提升核心素养
4.2 注重知识的综合应用,提升关键能力


