顺应“三新”趋势探索变式教学模式
——数学变式征集活动解析几何专题试题选登
(作者单位 姓名:江西上饶余干第一中学 邹荣华)
(作者单位 姓名:甘肃省嘉峪关市第二中学 彭长军)
(作者单位 姓名:江西上饶余干第一中学 叶新波)
(作者单位 姓名:陕西省宝鸡市麟游县中学 韩红军)
(作者单位 姓名:江西上饶余干第一中学 叶新波)
(作者单位 姓名:河北定州中学 赵伟娜)
【精选变式题组】
【母题1】(2022·江西余干一中)已知⊙O的方程为x2+y2=4,过M(4,0)的直线与⊙O交于A,B两点,则弦AB的中点P的轨迹方程为________.
【变式1】(知识变式)将母题中的“圆”换为“椭圆”

【变式2】(方法变式)将过圆外一点变为过圆内一点
已知⊙O的方程为x2+y2=25,过M(4,2)的直线l与⊙O交于A,B两点,则弦AB的中点P的轨迹方程为________.
【变式3】(综合变式)变圆中点弦为椭圆中点弦,变单空为双空,定点与两交点的位置由同侧变为异侧,同样可以用点差法处理问题.


(Ⅰ)求双曲线C的标准方程;
(Ⅱ)设Q为双曲线C右支上的一个动点,在x轴上是否存在定点M,使得∠QFM=2∠QMF?若存在,求出点M的坐标;若不存在,请说明理由.
【变式1】(知识变式)将“在x轴上是否存在定点M”变为“在x轴的负半轴上是否存在定点M”

(Ⅰ)求双曲线C的标准方程;
(Ⅱ)设Q为双曲线C右支上的一个动点,F为双曲线C的右焦点,在x轴的负半轴上是否存在定点M.使得∠QFM=2∠QMF?若存在,求出点M的坐标;若不存在,请说明理由.
【变式2】(知识变式)命题背景由双曲线变为椭圆,同为考查角度的两倍关系.

(Ⅰ)求椭圆C的方程;
【变式3】(综合变式)变换为倾斜角互补关系,探究定点.
已知圆C1:(x+5)2+y2=36,点C(5,0),点M是圆C1上的动点,MC的垂直平分线交直线MC1于点P.
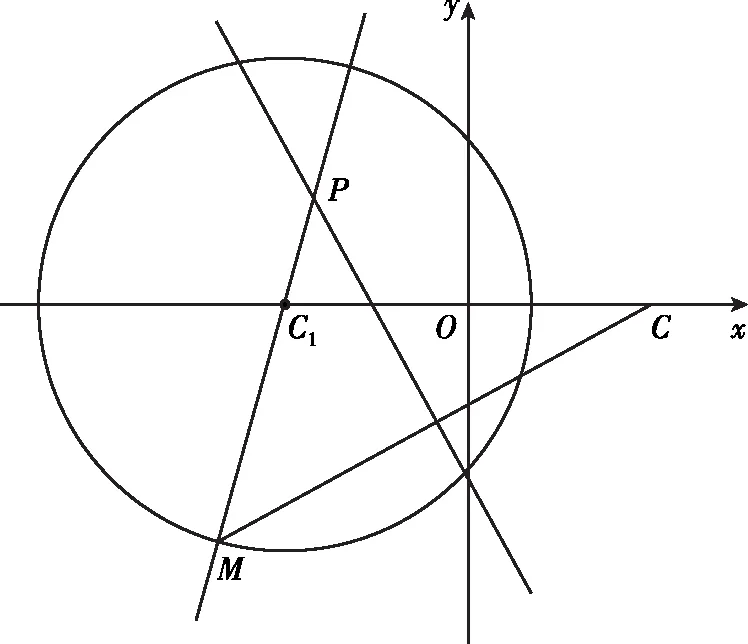
(Ⅰ)求点P的轨迹方程C2;
(Ⅱ)过点N(4,0)的直线l交曲线C2于A,B两点,在x轴上是否存在点G,使得直线AG和BG的倾斜角互补?若存在,求出点G的坐标,若不存在,请说明理由.
【母题详解及答案】
【母题1】【解题策略】本题考查圆中弦的中点轨迹问题,数形结合思想的应用
解法1:P为弦AB的中点→OP⊥PM→P在以OM为直径的圆上→求解即可;
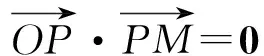
解法3:点差法→kAB=kPM→求解即可;
解法4:直线AB与圆联立求解→用参数表示点P坐标→消参即可
【解题思路】
【解法1】
点拨:利用圆中弦的中点得出垂直,从而构造外接圆进行求解.
连接OP,由圆的性质可知OP⊥PM,如图所示,

所以点P的轨迹是以OM为直径的圆且在⊙O内的部分,
以OM为直径的圆的方程为

结合图形可知所求轨迹方程为(x-2)2+y2=4(0≤x<1).
【解法2】
点拨:由圆的性质得垂直,利用垂直向量列方程求解.
连接OP,由圆的性质可知OP⊥PM,设P(x,y).

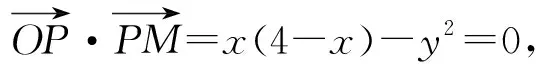
因为点P在⊙O内,所以点P的轨迹所在的圆在⊙O的内部,所以0≤x<1,
故所求轨迹方程为(x-2)2+y2=4(0≤x<1).
【解法3】
点拨:利用点差法列方程求解.
设P(x,y),A(x1,y1),B(x2,y2),
因为点A,B在⊙O上,所以x12+y12=4 ①,
x22+y22=4 ②.


化简得(x-2)2+y2=4.
因为点P在⊙O内,所以点P的轨迹所在的圆在⊙O的内部,所以0≤x<1,
故所求轨迹方程为(x-2)2+y2=4(0≤x<1).
【解法4】
点拨:直线的方程与圆的方程联立,用参数表示点P,再消参得轨迹方程.
设P(x,y),A(x1,y1),B(x2,y2),
易知直线AB斜率存在,设直线AB的方程为y=k(x-4),代入x2+y2=4得
(1+k2)x2-8k2x+16k2-4=0,
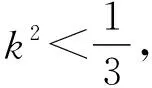
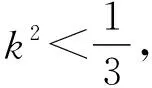
消去k得(x-2)2+y2=4,
故所求轨迹方程为(x-2)2+y2=4(0≤x<1).
(作者单位 姓名:江西上饶余干第一中学 邹荣华)

(作者单位 姓名:江西上饶余干第一中学 邹荣华)
【变式2】x2+y2-4x-2y=0.
(作者单位 姓名:甘肃省嘉峪关市第二中学 彭长军)
【变式3】x+4y-5=0.
x2+4y2-x-4y=0.
(作者单位 姓名:江西上饶余干第一中学 叶新波)


①当x0=2时,y0=±3.因为∠QFM=2∠QMF=90°,所以∠QMF=45°,于是MF=QF=|y0|=3,所以t=-1或t=5,即M(-1,0)或(5,0);
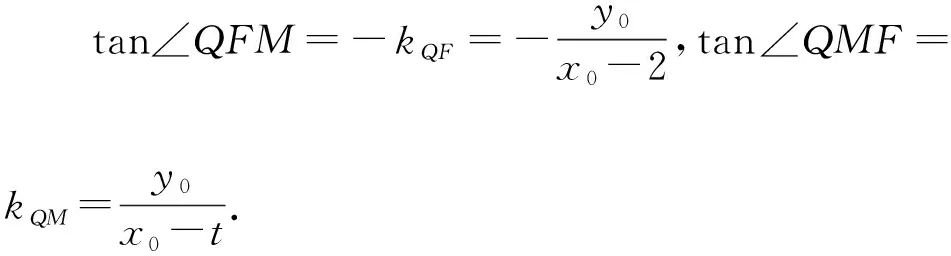
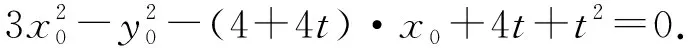
当y0=0时,t=-1,即M(-1,0)也能满足∠QFM=2∠QMF.
综上,存在满足条件的点M,其坐标为(-1,0).
(作者单位 姓名:陕西省宝鸡市麟游县中学 韩红军)

(Ⅱ)存在,m(-1,0).
(作者单位 姓名:陕西省宝鸡市麟游县中学 韩红军)

(Ⅱ)存在,定点P(0,1).
(作者单位 姓名:江西上饶余干第一中学 叶新波)



