浅埋海底隧道围岩应力复势函数显式解1)

金 波 田俊彤 方棋洪

* (湖南大学土木工程学院,工程结构损伤诊断湖南省重点实验室,长沙 410082)

† (湖南湖大建设监理有限公司,长沙 410082)

** (湖南大学机械与运载工程学院,长沙 410082)

引言

国内经济持续发展、城市规模不断扩大、城市之间联系愈发紧密,客流量与货物运输量急剧增加,为了缓解城市交通压力、节约土地资源和开发地下空间,建设一批市政管道和跨水域隧道成为最优方案.特别是在沿海城市,海底隧道具有抗震性能好、不影响货船航运、隐蔽性高和不受气候影响等优势而被广泛采用.这些隧道部分区段往往埋深较浅,建设中不可忽视地下水压、岩体自重以及地表边界上其他复杂工况的影响.准确得出隧道周边应力分布与变形对指导隧道设计以及安全施工具有重要的理论意义和工程价值.

20 世纪初,俄国力学家Kolosov[1]采用复应力函数法解决二维弹性静力学问题,Muskhelishvili[2]系统论述了弹性力学平面问题的复变函数法,极大促进该方法的应用与发展.保角映射能将复杂区域转化为简单规则区域,使得复变函数在研究平面含孔洞问题时具有明显优势,因此,平面问题复变函数方法在岩土工程领域得到了广泛应用.

深埋单孔隧道属于无限单连通域问题,研究中可忽略岩体重力梯度的影响,不同孔型的深埋隧道其映射函数均可采用Laurent 级数表示,对深埋隧道的理论研究已趋于成熟[3-17].采用复变函数方法研究浅埋隧道问题起步较晚,1997 年Verruijt[9-10]提出分式映射函数,将含圆孔的半平面岩石物理区域保角映射为像平面上同心圆环域,获得了在不考虑岩体重力影响,仅有孔口均布径向位移与均布径向面力边界条件时的解答;Verruijt 等[11]考虑周围岩体自重应力对开挖浅埋单孔隧道的影响,将未被开挖的初始状态、考虑岩体作用时开挖岩石等效合力状态和孔口附加等效载荷3 种状态的解叠加成为最终解;Verruijt 等[12]在原有复应力函数中增加了能够反映弹性体在不平衡力系作用下的影响项,给出了二维平面问题在不平衡力系作用下复应力函数的一般形式,并对孔口位移边值条件进行了研究.蔚立元等[13]、王志良等[14]和陆文超等[15]得到地面任意分布载荷下的围岩应力场;韩凯航等[16]基于复变函数法并结合柯西-黎曼方程得出浅埋隧道应力及位移函数的级数显式表达式;宋文杰等[17]求解了不排水黏土浅埋盾构隧道地层变位和地层应力;宋浩然等[18-19]与Fang 等[20]研究围岩自重及水的作用,将问题分解为四部分求解,分析水对隧道围岩应力的影响;杨公标等[21]研究在重力影响下的含空洞地层浅埋隧道围岩应力及位移解析解.

最近,许多学者对隧洞不均匀边界条件问题展开了研究.Lu 等[22-24]、Zeng 等[25-26]和Cai 等[27]研究了实际开挖过程引起的边界不平衡力分布,提出不平衡力系由整个开挖边界决定,并给出浅埋非圆孔隧道映射函数,对地表有水平初始应力作用的浅埋隧道、水工隧道以及马蹄形非圆孔隧道等工程问题进行了研究.申航等[28]研究矩形孔口径向位移边界条件下的应力场和位移场;文明[29]提出在重力作用下浅埋非圆形隧道力学分析的解耦保角映射方法.Lu 等[30]和Kong 等[31-33]利用傅里叶级数来表示圆形浅埋隧道横截面变形的统一位移函数,在地表水平以及边坡边界模型中考虑隧道“浮力效应”得到单孔隧道解析解,并在此基础上采用Schwartz 交替法得到双孔隧道解答;采用傅里叶级数表示出水下浅埋隧道周边复杂应力状态的统一应力函数,以此作为孔口应力边界条件,给出了应力和位移的弹性解析解.

采用平面弹性复变函数方法求解浅埋隧道问题一直存在复势函数系数求解困难的问题.Verruijt 等[12]在求解孔口应力边界条件问题时借助复势函数 φ(ζ)和 ψ (ζ)在像平面圆环域内的收敛性,假设1 阶正幂项系数为0,利用迭代方程组经过多次迭代(比如1000 或10000 次)直至高幂次项系数为非零常数,以此得到其余系数.Lu 等[30]推导时取 2N个线性组方程求 2N个未知数,并假定其余正负高幂次项为零,其中N需要足够大才能保证足够的精度.

本文利用无穷远点应力有界性对解析函数的Laurent 级数展开式幂次项进行了确定,从而得到1 阶正负幂次项系数,再根据边界条件所得迭代公式解出完整的解析函数.此方法区别于以上两种方法,通过从低次幂系数迭代求解至高次幂系数,复势函数每一项系数都能够用公式明确表示,使浅埋隧道复势函数求解更方便,更容易实现编程计算.以浅埋海底隧道孔口受不均匀应力边界条件为例,得出孔口应力幂级数解,与有限元数值解对比验证幂级数解的可靠性;研究了复势函数 φ (ζ)和 ψ (ζ)级数展开后取不同幂次项和不同函数系数对求解结果的影响机理;分析了浅埋隧道埋深对环向压应力的影响.此方法可求解半无限平面含孔洞问题,求解结果具有较高精度,将程序嵌入小型计算仪器中可方便工程应用.

1 问题描述和基本理论

根据文献[11-32]提出的海底隧道力学模型可知,所研究的浅埋单孔海底隧道位于完全饱和且均匀、各向同性的弹性含水地层中,力学模型如图1 所示.水平地表上作用有深度为hw,容重为 γw的海水,海水处于不可压缩的稳定状态.隧道半径为r,隧道中心至地面距离为h,岩石容重为 γ,侧压力系数为k0.将该力学模型分解为两部分(图2 和图3),其关系式如下

图1 海底隧道力学模型Fig.1 Mechanical model of subsea tunnel

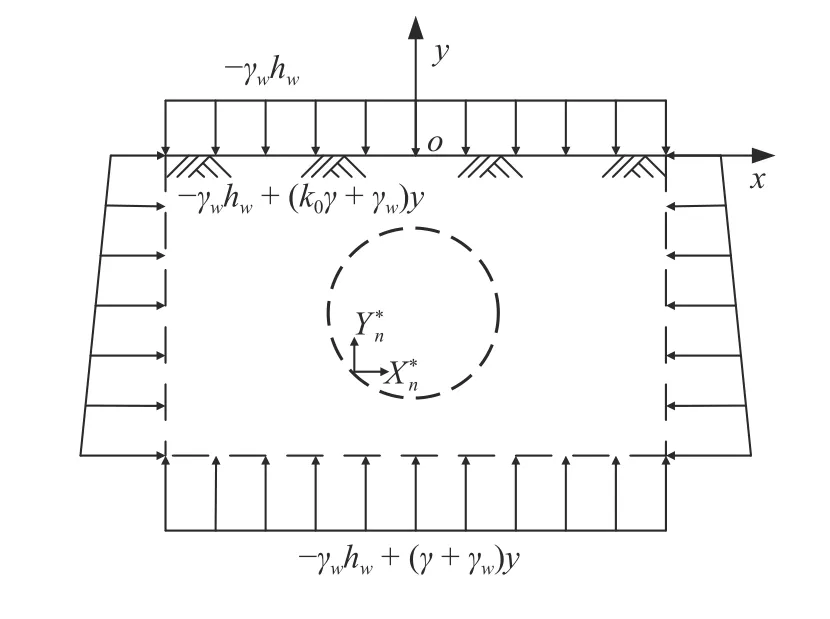
图2 第1 部分模型Fig.2 Part I model

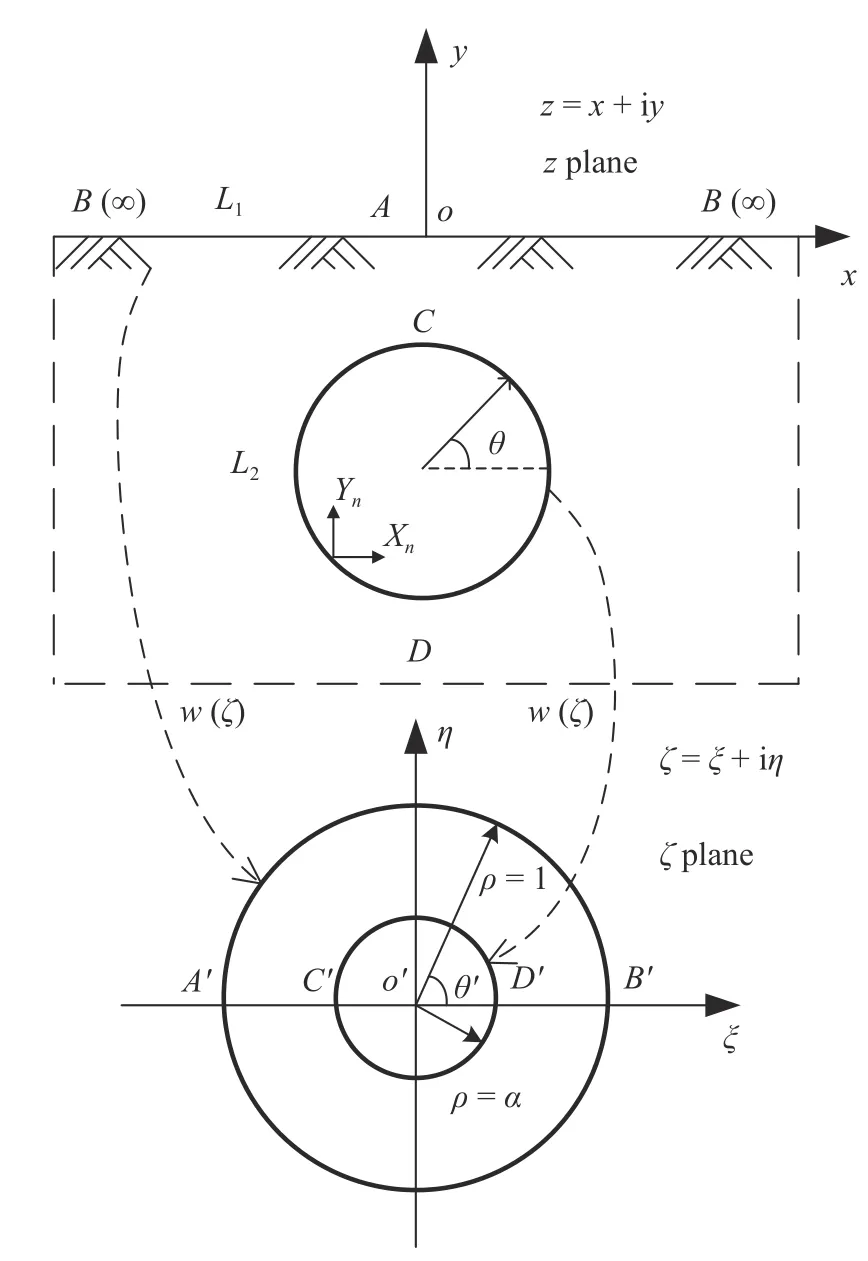
图3 第2 部分模型Fig.3 Part II model

第1 部分解答为

运用平面弹性复变函数法研究第2 部分模型的围岩应力.第2 部分为半无限平面含单圆孔模型,共包含地表和孔口两个边界条件,对于岩体任意点的应力和位移均可用复势函数 φ (z) 和 ψ (z)表示.可求得第2 部分应力解

式中,G为剪切模量,G=E/[2(1+μ)],对于平面应变问题K=3-4μ,μ 为泊松比,k0=μ/(1-μ).

复势函数 φ (z) 和 ψ (z)是区域内的单值解析函数,其形式如下

其中,φ0(z) 和 ψ0(z)为单值解析函数,可将其展开成Laurent 级数.在本文中考虑岩体自重和水压力,则Fx=0,Fy=πr2(γ+γw).

2 复数形式的边界条件

2.1 应力边界条件和映射函数

采用平面弹性复变函数解法的应力边界条件如下

其中,C为积分得到的复常数,Xn和Yn分别表示边界上一点沿x轴与y轴平行的面力分量,l和m是所讨论边界点的单位外法向量的方向余弦,如图4 所示.

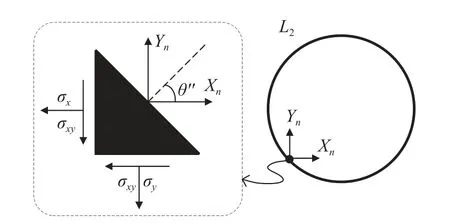
图4 隧道孔口任意点应力状态Fig.4 Stress state at any point of tunnel orifice

第2 部分解中地表没有施加载荷,则地表边界L1上有Xn=0,Yn=0,此时不失计算结果的有效性,复常数C可以假设为0,地表边界的应力边界条件可以表示为

图2 中的虚线表示未开挖的虚拟孔口,其与图3两模型叠加得到开挖后的模型如图1,开挖后孔口面力分量为0.在隧道孔口边界L2上施加面力分量Xn和Yn,该面力分量与图2 中虚拟孔口边界上面力分量大小相等,方向相反,孔口边界L2的应力边界条件表达式中复常数C不能再假设为0.

运用保角变换方法通过映射函数z=ω(ζ)将图3中Z平面中岩土区域映射到复平面 ζ区域上的圆环中,圆环外径为1,内径为 α.α是与隧洞埋深h和隧洞半径r有关的系数,其可通过如下确定.

将映射函数z=ω(ζ) 代入 φ0(z) 和 ψ0(z)中有

2.2 地表边界条件求解

为方便求解和表示复平面圆环上的点,令ζ=ρσ, ρ为半径,σ=eiθ′.图3 中z平面地表边界y=0 映射到 ζ平面的单位圆|ζ|=1,地表无穷远点对应点 ζ=1,则地表边界在复平面中用 ζ=σ表示.将φ(z) 和 ψ(z) 代入地表应力边界条件得到z平面的表达式

将映射函数z=ω(ζ)代入式(20),其中

地表边界 ζ=σ,可将式(20)左右各转换为 ζ平面中有关 σ的表达式,分别如下所示

Ak可展开为

将式(23)与式(25)相应的k阶幂指数对应有

为确定函数 φ0(ζ) 和 ψ0(ζ)中ak与bk的系数还需要通过孔口边界条件得到其余关系式.

2.3 孔口边界条件求解

隧道孔口x2+(y+h)2=r2经过映射成复平面ζ上半径为 α的单位圆 ζ=ασ.在孔口边界为

将复势函数 φ (z),ψ (z)和映射函数式(16) 代入边界条件(27)变换为有关 σ的表达式

将式(29)左侧展开

式(29)右侧用级数形式表示

将式(26)代入式(32)中可以得到迭代公式如下

当k=0和k=1时

可求得复常数C,其实部与虚部为

其中Ak已由地表边界得出,Bk可根据隧道孔口边界求得.将式(2)、式(13)和映射函数(16)代入孔口应力边界条件(27)右侧积分项中并将其展开为有关 σ的多项式得到式(39),则式(29)左侧可以展开为式(40),式(40)通过同幂次项系数对应可得到级数系数,复常数C已知从而求得Bk

3 解析函数求解与说明

将复势函数 φ0(ζ) 和 ψ0(ζ)Laurent 级数展开,其中未知系数ak和bk可由迭代式(33)和式(34)求出,但当k=0和k=1时得到相同的等式,则无法直接求解a-1和,其余ak和bk也无法根据迭代公式求得.为解决这一问题,利用无穷远点应力有界性提出一种求解方法.在图3 模型中仅有隧道孔口边界L2施加载荷,则距离边界L2无穷远的岩体应力有界.为保证无穷远点应力有界性这一条件,根据式(3)和式(4),则复势函数可表达为

3.1 解析函数求解

将z=w(ζ)代入上式,并将映射函数中含 ζ分式级数展开为

从上式可知当k≤-2 时有ak=0和bk=0.

由式(35)得

式(26)中k=0时,有

将式(46)和式(47)实部与虚部分开计算,再采用复变函数方法能够求出幂级数解工况中 Re(a-1)值为趋于0 的极小值,假定 Re(a-1)=0,则a1实部 Im(a-1)和 Im(a1)可由下式准确求得

根据迭代式(33),有

根据地表边界条件(26)可求得系数bk

式(48)～式(53) 即为复势函数 φ0(ζ)和ψ0(ζ)Laurent 级数展开中各未知系数的求解公式.

3.2 求解方法说明

从映射函数式中可知点 ζ=1为奇点,由于这一奇点的存在给解析计算带来很大的困扰.从3 个不同的方向趋近于该奇点分别对应物理平面中岩体的3 个无穷远处.在 ζ平面单位圆 ζ=eiθ′上,当 θ′→0和 θ′→2π其分别对应z平面地表边界无穷远点x=+∞和x=-∞处,ζ沿ξ轴ζ →1对应无穷远点y=-∞处.同时表达式1/(1-ζ)在 |ζ|＜1区域内收敛,可以表示为幂级数,但其在奇点所处的单位圆上,不能将其展开为幂级数而无法采用幂级数解法.

为保证求解精准性和计算的可行性,我们重新定义地表边界L*(如图5 所示)为z平面中y→0的直线和 ζ平面中ζ=(1-t)σ,t∈(0,0.1)的近似单位圆.当t足够小时,新定义的地表边界L*将趋近于原地表边界L1,这不仅能够确保边界条件与原地表的边界条件相同,还能确保岩体映射后的讨论域 ζ均在表达 式 1/(1-ζ)的收敛域内.虽然 ζ平面上边界L*(ρ=1-t)和边界L1(ρ=1)所表示的物理含义不同,但在解析计算时可以将 ρ=1-t近似为 ρ=1,这并不影响最后的计算结果.

图5 L*边界示意图Fig.5 L* boundary diagram

4 应力求解

将映射函数代入式(3)和式(4)得到迪卡尔坐标系下的应力求解公式

在极坐标中各应力分量的关系式为

将复势函数 φ (ζ) 和 ψ (ζ)代入式(54)～式(57)即可得到不同坐标系下的应力分量.

5 不同方法对比

当本文浅埋海底隧道模型所含参数hw=0 和γw=0 时即可简化为文献[22]中考虑重力和任意侧向应力作用下的弹性半平面含圆孔模型.为了验证本文方法的准确性,对侧压力系数k0=0.5下的工况求解,将其与Lu 等[22]得出的结果和有限元结果进行对比.复势函数 φ0(ζ) 和 ψ0(ζ)分别计算至a6和b5.分析孔口应力时所取计算范围与文献[22]相同即隧道右半部分,α=0°为隧道底部,α=180°为隧道顶部.其余参数也与文献[22] 中参数相同: μ=0.3,E=10.0 MPa,γ=25.0 kN/m3和h/r=2.0.极 坐标系中的计算结果对比见图6.

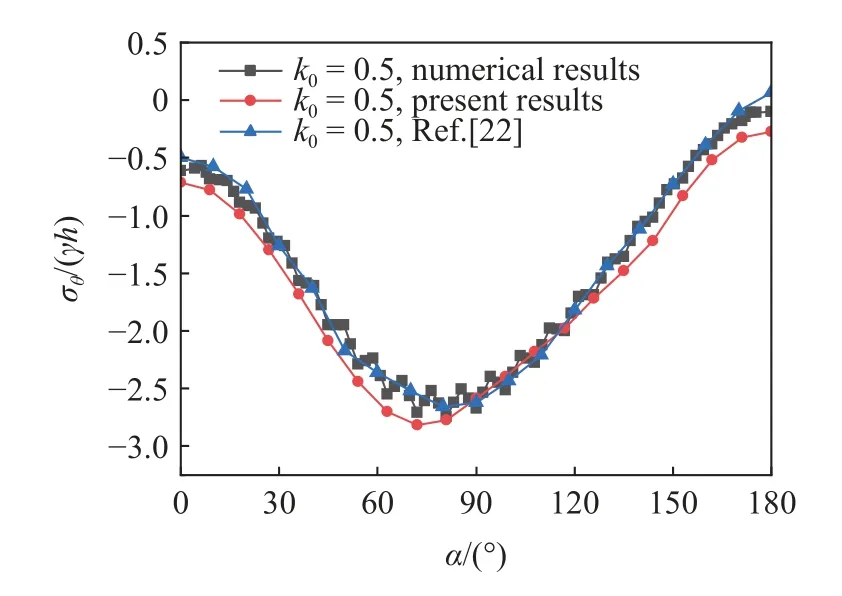
图6 不同方法计算结果对比Fig.6 Comparison of calculation results by different methods

从图6 可知,本文解得的复势函数所计算的孔边环向应力与Lu 等[22]得出结果和有限元结果基本相同.与其他两种方法相比,本文计算结果压应力偏大.当k0=0.5,h/r=2.0时,Lu 等[22]计算复势函数需求解32 元线性方程组.本文只需根据复势函数系数的显式求解式(52)和式(53)分别求出系数a6与b5,根据不同精度需求可确定k的取值,k取值越高精度越高,同时本计算过程也减少了依靠地表和孔口边界条件所求系数Ak和Bk的需求.因此,在满足工程精度需求下,运用复势函数显式计算公式求解,计算过程简便,计算量小.

6 算例分析

为了验证本文理论方法的可靠性,将本文在迪卡尔坐标系下的理论解答与数值计算结果进行对比.此例定义参数如下: 隧道孔洞半径r=4 m,埋深h=10 m,海水深度hw=2 m,海水重度 γw=10 kN/m3,土体重度 γ=25 kN/m3,泊松比μ=0.3,弹性模量E=200 MPa.规定应力拉为正,压为负.利用ANSYS 软件建立第2 部分解答的有限元模型计算数值解,模型尺寸为100 m×60 m,采用PLANE183单元,共划分单元3028 个,图7 为网格划分情况.模型上边界为自由边界,对模型左右边界施加x向约束,下边界施加y向约束,隧道圆形孔口施加与幂级数解边界L2相同的面力.

图7 有限元模型网格划分结果Fig.7 Finite element model meshing results

本文主要是对第2 部分模型(图3)采用复变函数方法求解,同样利用ANSYS 对第2 部分解答模型进行模拟.通过有限元模拟得出应力分量,和的应力云图,如图8 所示.利用MATLAB 软件编程计算得到幂级数解.分别将幂级数解和有限元结果与第1 部分解叠加得到隧道开挖后的围岩应力.孔边应力幂级数解和数值解对比见图9.

(2) 环青藏高原东侧第一阶梯坡降区的复杂地形地貌，是川藏高速公路崩塌发育的根本原因之一，其地形陡、坡降大，岷江、大渡河流经的高山峡谷区，为崩塌危岩的发生奠定了良好的地形地貌基础。

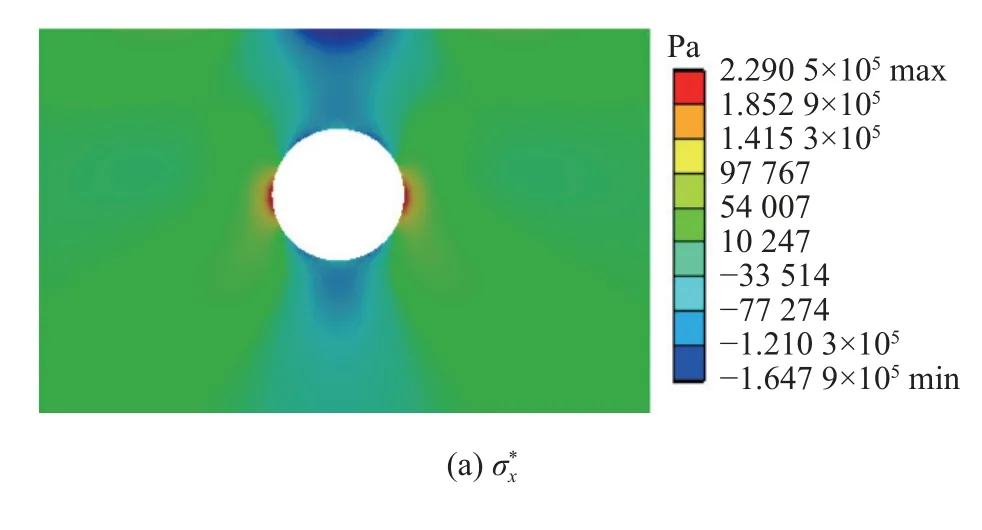
图8 第2 部分模型有限元应力云图Fig.8 Finite element stress nephogram of part II model

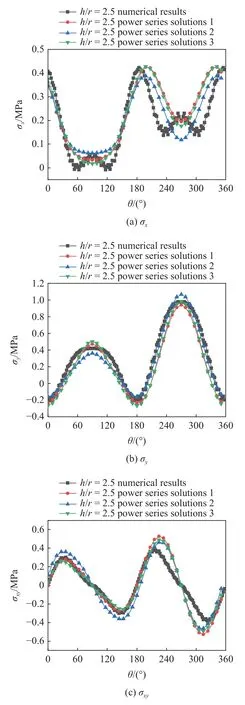
图9 不同系数的幂级数解和数值解对比Fig.9 Comparison of power series and numerical solutions with different coefficients

6.1 数值解对比

从图9 可以看出幂级数解(power series solutions 1)与数值解能较好吻合,验证了本文方法的正确性.当 θ ∈[0°,180°]时为隧道上半部分,幂级数解与数值解得到的孔边应力(σx,σy和 σxy)基本一致;但当 θ ∈(180°,360°)时为隧道下半部分,幂级数解与数值解具有一定的差异.幂级数解与数值解产生的计算差异是由所选映射函数造成的.与数值解相比,幂级数解得到的 σy略小于数值解,而孔口下半部分各点应力分量 σx与σxy的绝对值则比数值解的绝对值大.幂级数解最终计算结果比数值解相对保守.

6.2 解析函数系数影响分析

为了研究单值解析函数 φ0(ζ)与 ψ0(ζ)中系数ak与bk取不同项数对运算结果的影响,取3 组ak与bk展开不同项数时的幂级数解进行对比.系数展开项数见表1,幂级数解对比见图9.

表1 项数展开表Table 1 Number of terms expansion table

从图9 中可以看出power series solutions 1 与power series solutions 3 在3 个应力分量 σx,σy和 σxy的计算结果都基本保持一致,power series solutions 2与其结果相比在不同位置、不同应力分量上均有一定的差距.特别在隧道孔口上半部分 θ ∈[0°,180°],power series solutions 3 要优于power series solutions 2.

从中可以得出单值解析函数 φ0(ζ)对最终结果准确性的影响要大于 ψ0(ζ).求解时为了保证计算结果的准确性,φ0(ζ) 需要展开足够多的项,ψ0(ζ)则至少要展开b-1～b1项.

6.3 隧道埋深影响分析

为了分析浅埋隧道埋深对环向应力的影响,隧道中心埋深h分别取8,10,12 和14 m,单值解析函数 φ0(ζ) 与 ψ0(ζ)中系数ak与bk展开项与power series solutions 1 相同,其余条件与参数不变,不同隧道埋深孔口应力情况见图10.隧道底部(θ=270°)及两侧孔腰处(θ=200°或 θ=340°)环向压应力随着隧道埋深h增大而增大,而孔口顶部(θ=90°)环向压应力无显著变化.隧道埋深增加1.75 倍,腰部及底部环向压应力增加3～4 倍.隧道腰部与底部环向应力的差值也随着隧道埋深的增大而增大.由此可见隧道埋深对隧道底部及腰部环向压应力的大小影响较大,且对腰部的影响最为显著.

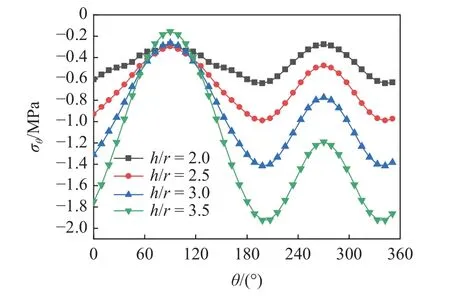
图10 不同埋深孔口环向应力对比Fig.10 Comparison of annular stress at orifices with different burial depth

7 结论

本文运用平面弹性复变函数方法研究了浅埋圆孔海底隧道在围岩重力和海水静水压力作用下的围岩应力幂级数解.采用分式映射函数将半无限平面含圆孔模型映射为像平面上的圆环域,在圆环域内将复势单值解析函数展开为Laurent 级数.利用无穷远点应力有界性对级数展开式的幂次项进行确定,根据级数系数迭代公式得到复势函数的显式解,运用应力分量的复变函数表达式得到孔边各点的应力分量,将幂级数解与有限元结果对比得出以下结论.

(1) 为保证无穷远点应力有界,根据应力求解公式,将复势单值解析函数 φ0(ζ) 和 ψ0(ζ)的Laurent 级数重新定义为负一项至正无穷项.在 R e(a-1)=0条件下,由地表与孔口边界条件得出复势解析函数系数显式解,此解可迭代求得其余系数,从而实现级数系数从低次幂迭代至高次幂这一过程,使得浅埋隧道复势函数求解更方便.

(2)幂级数解与有限元数值解能很好吻合.在隧道上半部分(θ ∈[0°,180°]) 幂级数解与数值解得到的孔边应力(σx,σy,σxy)基本一致;在隧道下半部分(θ ∈(180°,360°))由于所选映射函数的影响,幂级数解得到的 σy略小于数值解,σx与 σxy的绝对值则比数值解的绝对值大.幂级数解最终计算结果较数值解偏保守.

(3) 单值解析函数 φ0(ζ)对最终结果准确性的影响要大于 ψ0(ζ).求解时为了保证计算结果的准确性,φ0(ζ)需 要展开足够多项,ψ0(ζ)则 至少要展开b-1～b1项.

(4) 随着海底隧道埋深增大,隧道底部及两侧孔腰处的环向压应力随之增大.隧道埋深增加1.75 倍,腰部及底部环向压应力增加3～4 倍;而孔口顶部环向压应力无显著变化.隧道腰部与底部环向应力的差值也随着隧道埋深的增大而增大.隧道埋深对隧道底部及腰部环向压应力的大小影响较大,且对腰部的影响最为显著.

数据可用性声明

支撑本研究的科学数据已在中国科学院科学数据银行(science data bank) ScienceDB 平台公开发布,访问地址为https://www.doi.org/10.57760/sciencedb.j00140.00011 或http://resolve.pid21.cn/31253.11.sciencedb.j00140.00011.