高超声速火星进入环境中颗粒运动特性研究1)

邢好运 刘 卓 汪 球 赵 伟 高亮杰 刘中臣 钱战森

* (中国科学院力学研究所高温气体动力学国家重点实验室,北京 100190)

† (中国科学院大学工程科学学院,北京 100049)

** (中国航空工业空气动力研究院,沈阳 110034)

引言

由于火星的大气条件和地球比较相似,火星探测一直是国际深空探测发展的热点.截止目前,全球各国一共向火星进行了48 次发射,但在所有的发射中,实现真正意义上软着陆的国家只有中国与美国.在所有着陆尝试中,有10 次完全成功的火星探测器软着陆,成功的概率仅约为50%,因此火星也被称为“探测器坟场”[1-3].特殊且缺乏足够数据库支撑的火星大气环境及由此引起的进入飞行气动特性不确定性是造成探测器飞行安全隐患的主要原因之一,亟待气动力/热的精确预测来提升飞行器气动布局和热防护系统设计.

火星大气与地球大气除气体组分、密度等不同外,还有一个特别之处在于火星大气中存在微小的尘埃颗粒,主要由铁氧化物和硅氧化物组成.在火星平均每3～4 年就会发生一次全球级的沙尘暴,灰尘颗粒甚至能达到60 km 的高空,根据Viking 着陆器的观测以及对火星大气中垂直风强度的估计,大尺寸颗粒(直径约为5～10 μm)在一次大型沙暴开始后的20～50 d 内依旧会悬浮在大气上空[4],而在高超声速来流中,即使颗粒的质量浓度较低,颗粒的存在也会导致探测器表面热流显著增加[5].因此,开展含颗粒火星大气环境对飞行器气动特性的影响研究十分有必要,它有助于降低防热结构设计的冗余量或提升飞行器性能.

尘埃颗粒对高超声速飞行器火星进入过程中的影响研究最早是由Papadopoulos 等[6]通过数值模拟进行评估,其结果表明火星沙尘暴会对飞行器热防护系统(thermal protection system,TPS)表面造成严重侵蚀;然而,Palmer 等[7]对此重新评估,认为其高估了由于颗粒撞击造成的附加质量损失,两者的主要差异源于他们使用了不同的尘埃颗粒模型.Majid等[8]模拟了(mars sample return orbiter,MSRO)在尘埃颗粒环境下的进入过程,结果表明颗粒撞击表面引起的热流密度与对流热相比可以忽略不计;Vasilevskii等[5]发现在无扰动流中添加直径为0.15 μm 的微小颗粒,即使在浓度较低(约为1%)时,模型临界点区域的热流通量也会显著增加.Palmer 等[9]最近也对这个问题进行了全面的概述,并模拟了ExoMars Schiaparelli 飞行器在3 种不同的沙尘暴条件下的进入过程,其结果表明,在全球性沙尘暴发生时,驻点处的隔热层侵蚀量约为2.1 mm,占TPS 厚度的17%,而在区域性沙尘暴发生时侵蚀量仅为0.35 mm,在沙尘静止条件下的侵蚀量可以忽略不计.另外,Ching等[10]发现热通量预测对阻力系数非常敏感;且Ching 等[11-12]最近的工作也表明,使用不同的阻力模型和自由流颗粒分布时,进入过程中飞行器上某些位置的表面衰退出现显著差异.虽然目前学者已经提出了模拟该问题的一些方法,但是微尺寸颗粒相关的理论模型还不完备,不同的研究人员的结论之间也存在分歧,有必要进一步研究含颗粒环境下高超声速飞行器火星进入过程的气动问题.

本文基于Euler-Lagrange 框架,采用单向耦合方法,模拟ExoMars Schiaparelli 进入舱在尘埃颗粒环境下的火星进入过程,考虑高温相变模型对不同粒径颗粒运动轨迹的影响,模拟不同尺寸颗粒的运动轨迹以及计算对应的撞击分数,并选取模态半径为0.35 μm 的火星尘埃颗粒分布模型来计算撞击能量分数,相关研究有助于理解尘埃颗粒的运动规律,并可帮助建立尘埃颗粒对飞行器表面的侵蚀模型.

1 颗粒运动模型

当考虑火星大气含灰时,数值模拟即变成一个两相流问题,需要考虑颗粒与流场之间的耦合方式,一般通过分散相的体积分数αp来选择适当的耦合方式,包括单向耦合、双向耦合以及四向耦合[13].火星大气尘埃颗粒的体积分数αp约为10-6量级[14],含量较低,因此本文的计算中选用单向耦合方法来进行计算,即仅考虑流场对颗粒的作用而不考虑颗粒对流场的作用,单向耦合也是国内外学者研究这个问题最常用耦合方式[6,9,15-16].另外,本文所做的主要假设还包括:

(1) 火星尘埃为离散的固体球形颗粒,密度为2940 kg/m3[6];

(2) 只考虑颗粒受流场对流传热影响,不考虑其受到的辐射加热;

(3) 颗粒自身不存在温度梯度,且颗粒在流场中一直为球形,在模拟过程中,相变(蒸发、熔化或升华)均匀,颗粒不发生碎裂;

(4) 假定质点运动仅为平动,不考虑Magnus力、附加质量力、Basset 力、Saffman 升力和其他外力(重力、电磁力);

(5) 不考虑颗粒间的碰撞.

1.1 颗粒动力学模型

颗粒运动采用拉格朗日方法进行分析,可求得颗粒轨迹上的具体信息.对颗粒运动使用牛顿第二定律进行计算,仅考虑流场作用在颗粒上的阻力

其中,ΔV为颗粒所在位置流场速度Vg与颗粒自身速度Vp的差值,即ΔV=Vg-Vp,mp为颗粒质量,Cd为颗粒阻力系数,rp为颗粒半径,ρg为颗粒所在位置流体的密度,进一步由式(1)可得

其中,ρp为颗粒密度,dp为颗粒直径.本文阻力系数模型采用Henderson[17]提出的阻力模型,该模型适用于连续、过渡和自由分子流状态的球体阻力系数的计算,同时还考虑了相对马赫数Mrel、相对雷诺数Rerel以及颗粒自身温度Tp与流场温度Tg的影响,Henderson 模型与Bailey 等[18]在球体上的实验数据以及20 世纪初的理论推导保持一致,Henderson阻力模型计算如下.

对于Mrel＜ 1

最后通过Lagrange 方法来计算颗粒的位置,计算方法如下

由于本文开展的是二维模拟,因此式中Xp=[xp,yp],Vp=[up,νp].Xp代表颗粒所在位置,Vp代表颗粒速度,xp和yp为颗粒在x,y方向的位置分量,up和νp为颗粒在x,y方向的速度分量.

1.2 颗粒热力学模型

在飞行器进入火星大气的过程中,激波后流场温度可达上千度,温度可能会高于颗粒的融化温度,使颗粒发生相变.此外,颗粒的温度还会影响阻力系数的计算.因此,本文将考虑流场向颗粒传热导致其温度升高及相变发生,具体的计算公式如下

式中,Ch为对流传热系数,通过式(8),可以得到颗粒表面温度的计算式为

要计算颗粒表面温度Tp的变化,需要确定颗粒的对流传热系数Ch,其与Nusselt 数(Nu) 相关,Nu表示在边界处对流换热与热传导的比值

对于颗粒来说,特征长度L为颗粒直径,κg为颗粒周围流体的热传导系数.Nusselt 数表达式通常用颗粒马赫数和雷诺数表示,因此也是流体速度、黏性和流体导热系数的函数.本文中使用Fox 等[19]建立的Nusselt 数计算模型,该模型考虑了可压缩和非连续流动影响,且该式适用于亚声速和超声速颗粒马赫数

颗粒进入激波层之后会吸热,表面温度将升高,一旦超过颗粒自身的融化温度将会导致颗粒直径的减小,火星大气中颗粒的成分一般为SiO2,熔化温度约为1990 K,在单向耦合的假设下,仅考虑颗粒自身直径的变化而不考虑由颗粒相变导致的流场质量增加,具体的计算模型如下

式中,ζ为相变潜热,SiO2的相变潜热为8.6 MJ/kg;Tvapor为汽化温度,对于球形颗粒,式(12)可以转化为

需要注意的是,颗粒温度首先达到的是熔化温度,即1990 K,之后达到Tvapor才会蒸发,而在熔化温度与蒸发温度之间时,假设液态的部分附着在固态表面,颗粒质量不变;颗粒的汽化温度Tvapor随表面压力的增加而升高.本文采用Schaefer 等[20]提出的汽化温度线性拟合模型,该模型与参考文献[21]中给出的实验数据相吻合,在该模型中,气体压力p的单位为bar (1 bar=1.0×105Pa)

2 颗粒定位及流场信息插值方法

2.1 颗粒定位方法

使用欧拉-拉格朗日方法,我们需要确定颗粒在每个拉格朗日时间步长时所处的网格位置.无论是使用单向耦合还是双向耦合,拉格朗日计算都需要这些信息,这是由于计算需要在每个拉格朗日时间步长将流场的性质插值到当前颗粒位置.本文使用文献[8]中的颗粒定位方法,为了确定一个颗粒是否在一个给定的网格内,从逆时针方向对网格的各节点进行编号,从颗粒到每个网格节点定义向量,如图1 所示.

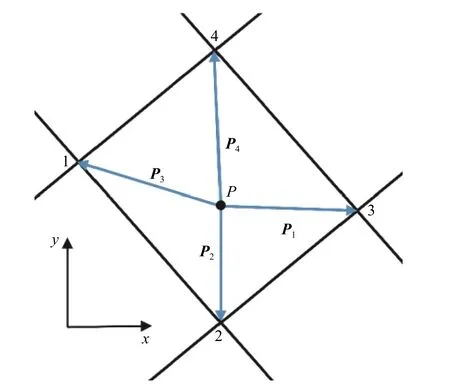
图1 颗粒定位示意图Fig.1 Particle locating algorithm description

如果颗粒满足下列条件,则认为该颗粒位于图1 所示网格内

颗粒只有在计算程序运行初期时需要通过对全流场网格进行遍历定位,一旦颗粒初始所在网格位置确定之后,在随后的过程中,通过时间步长的限制,将颗粒的移动距离限制在相邻网格中.在本文的工作中,定义了颗粒CFL 数用于限制颗粒在单个时间步长内的位移距离

式中,dt为时间步长,Δx为颗粒所在网格最小尺寸,Vp为颗粒速度,CFLp为颗粒CFL 数,通过颗粒CFL 数的限制,颗粒在单个时间步长内最多只能位移至相邻网格,一旦颗粒初始位置确定后,颗粒定位只需要对颗粒所在网格以及相邻的网格进行定位即可.由于过激波后温度梯度和速度梯度较大,在激波附近将设定更小的颗粒CFL 数以限制颗粒在单个时间步长内的位移距离,在本文计算中,当颗粒运动到激波所在的网格内(本文根据密度梯度定义,当颗粒所在网格密度梯度大于5 kg/m4时)时将其CFL数设为0.01.

2.2 流场信息的插值方法

本文考虑的火星颗粒尺寸均在微米量级,而火星探测器的直径一般为米量级,在划分网格时,尘埃颗粒的尺寸一般远小于网格尺寸.为了得到颗粒所在位置处的流场信息,在Euler-Lagrange 框架下,无论哪种耦合方式,都需要通过流场信息向颗粒所在位置进行准确插值,插值方法有很多种,如Newton插值法和Lagrange 插值法,为了适应不同的计算域网格类型,本文采用反距离加权(IDW)插值方法[22].

如图2 所示,Z0为待求插值点,Z1～Z5为已知点信息,计算未知点到已知点的距离分别记为d1～d5.

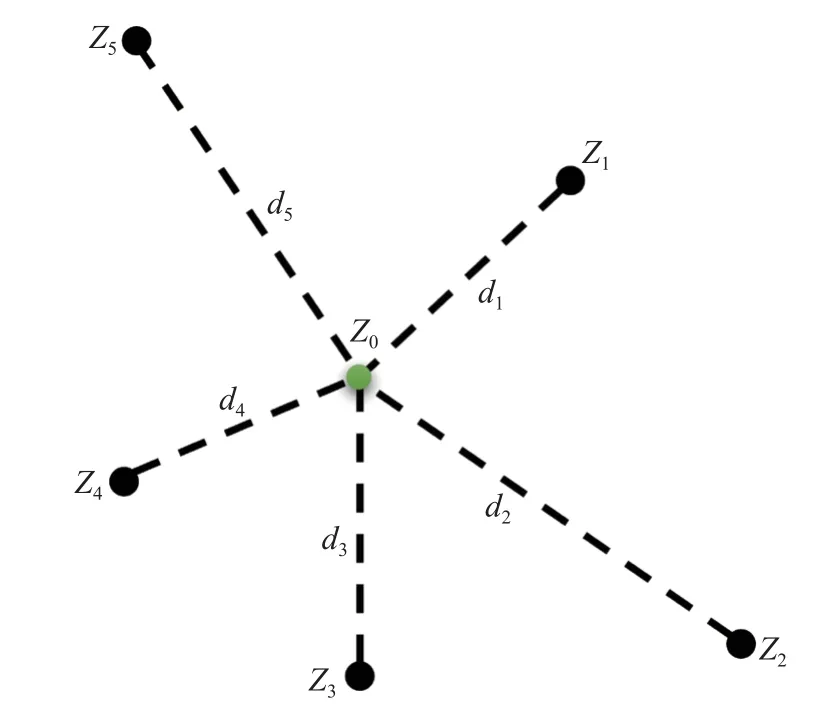
图2 IDW 插值模型示意图Fig.2 Schematic of IDW interpolation model

对Z0点的插值公式如下

IDW 插值方法也适用于非结构网格,一旦颗粒位置确定后,通过颗粒附近网格点上的信息对颗粒所在位置进行流场信息插值,从而进行颗粒的后续计算.

3 计算模型与程序验证

3.1 计算模型及流场程序验证

本文选用2016 年10 月进入到火星大气的ExoMars Schiaparelli 进入舱作为计算模型,该舱防热罩为球锥外形[23],直径为2.4 m (Rb=1.2 m),头部半径Rn=0.5Rb,肩部半径Rs=0.05Rb,其外形如图3 所示.Schiaparelli 太空舱的任务目标之一是在沙尘暴丰富的环境中进行火星大气风速、湿度、压力、大气颗粒特性以及火星表面温度的测量,虽然在着陆的过程中由于导航数据的计算错误,进而使降落伞过早释放导致任务失败,但其传送回的遥测数据详细记录了飞行轨迹相关信息,因此选用Schiaparelli 提供的自由来流条件作为输入来计算流场并进行颗粒侵蚀分析.

图3 Schiaparelli 飞行器与计算域Fig.3 Configuration of Schiaparelli and the calculation region

Gülhan 等[24]给出了Schiaparelli 飞行轨迹过程中的自由来流条件,本文选取30 km 高度的自由来流条件进行后续计算分析,即来流密度ρ=1.322 ×10-3kg/m3,速度u=2913.7 m/s,温度T=190.1 K.

Ching 等[12]开展了20°攻角和0°攻角进入条件下的三维模拟,发现不同攻角造成表面侵蚀差异可以忽略不计,因此本文采用二维轴对称热化学非平衡数值模型,对流项采用AUSMPW+格式进行离散[25],时间推进使用LU-SGS 格式[26],黏性项使用中心差分.化学反应模型采用Johnston 于2014 年提出的5 组分(CO2,CO,O2,O,C)二氧化碳模型,热力学非平衡效应采用双温模型.振动能松弛采用Landau-Teller 模型,CO2的振动松弛时间由Camac[27]给出,其余组分松弛时间由Millikan 等[28]的关系式给出.壁面边界条件为非催化等温壁面,壁面温度Tw=300 K.同时,计算程序基于MPI 并行处理以加快求解速度.

本文首先通过与程序LAURA[29]在两个相同工况下的计算结果对比来验证流场计算程序,具体工况参数如表1 所示,两状态均为中高焓工况,驻点线存在较大占比的热化学非平衡区域,由于热化学非平衡会显著影响激波脱体距离,因此通过MSL 进入器的无量纲激波脱体距离 Δ/R对程序的热化学非平衡流动模拟准度进行验证,两组工况下的结果如图2所示,本文计算结果与文献数据吻合较好.

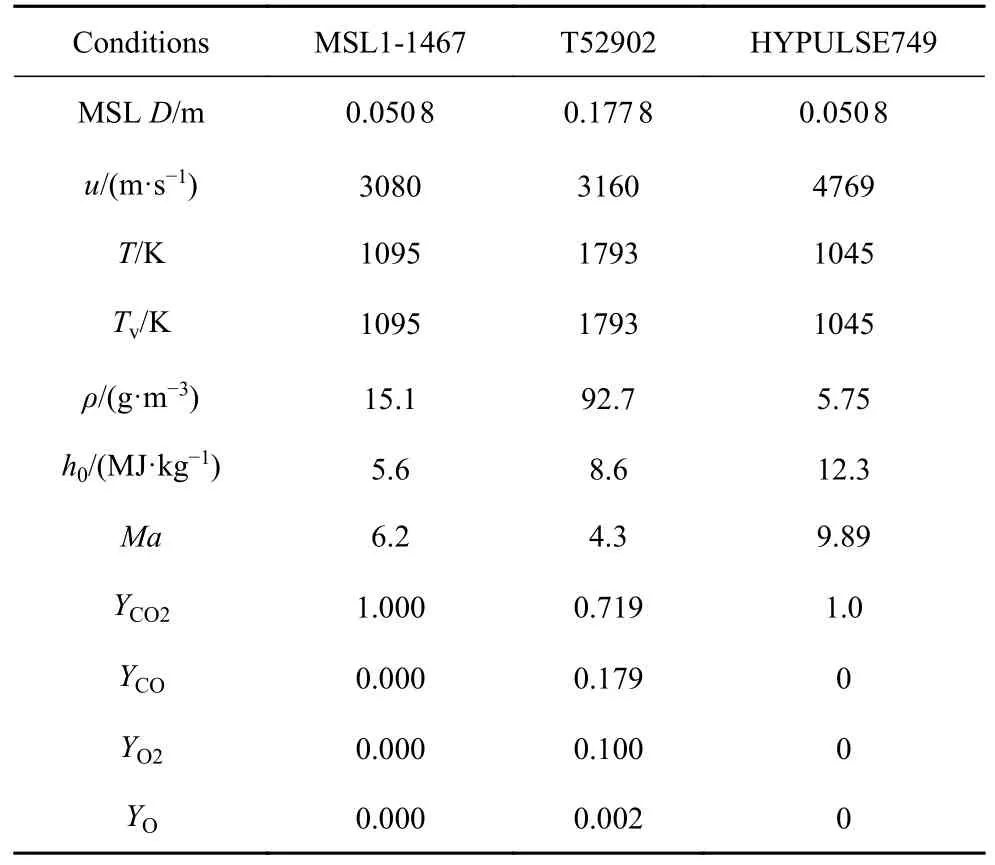
表1 程序验证的来流条件Table 1 Freestream conditions for program test

除激波脱体距离外,为了验证模拟结果,本文对参数为表1 中HYPULSE749 状态的自由来流进行壁面热流计算,将数值结果与密歇根大学开发的LeMANS 求解器[30]以及NASA HYPULSE 膨胀管的气动试验数据[31]进行了对比,计算中CO2各个振动模态松弛速率统一采用弯曲模态速率,壁面边界条件为300 K 等温无滑移非催化壁面,计算外型为Mars Pathfinder 前体,其与MSL 探测器结构类似.图4 给出了本文程序与LeMANS 在HYPULSE749工况下壁面热流的计算与试验数据的对比结果,其中,试验数据的测量不确定度包含试验标准偏差以及试验精度误差,根据文献[31],试验数据的测量不确定度为 ±11%.结果表明,本文计算程序与LeMANS 求解器得到的壁面热流值接近,且均在NASA HYPULSE 膨胀管的气动试验数据误差范围之内.通过对比可以认为本文流场计算程序模拟高温热化学非平衡流动具有较好的准确性,计算结果对比见表2.

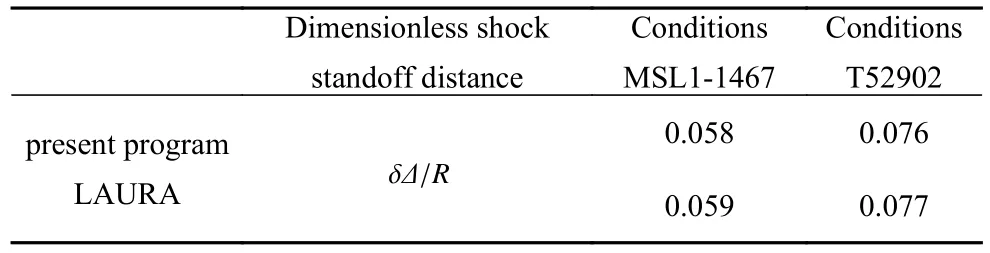
表2 本文程序和LAURA 的无量纲激波脱体距离计算结果对比Table 2 Comparison of shock standoff distances of sphere-cone model calculated by different codes

图4 壁面热流计算结果对比Fig.4 Comparison of surface heat flux calculation

3.2 颗粒计算程序验证

本文通过与Ching 等[10]在相同来流条件下不同初始位置颗粒在流场中的运动轨迹进行对比来验证颗粒计算程序,计算模型为球体,其半径为Rs=0.006 m,来流气体组分为N2,来流马赫数Ma∞=6.1,总压Pt,∞=17.5 bar,总温Tt,∞=570 K,壁面温度Twall=300 K;颗粒密度ρd=2264 kg/m3,颗粒直径dp=0.19 μm.两颗粒初始位置与驻点线距离ds分别为0.1 mm 和1.8 mm;本文使用的颗粒阻力模型及Nusselt 数计算模型均与文献[10]相同,图5 为颗粒运动轨迹本文计算程序与文献数据对比结果.

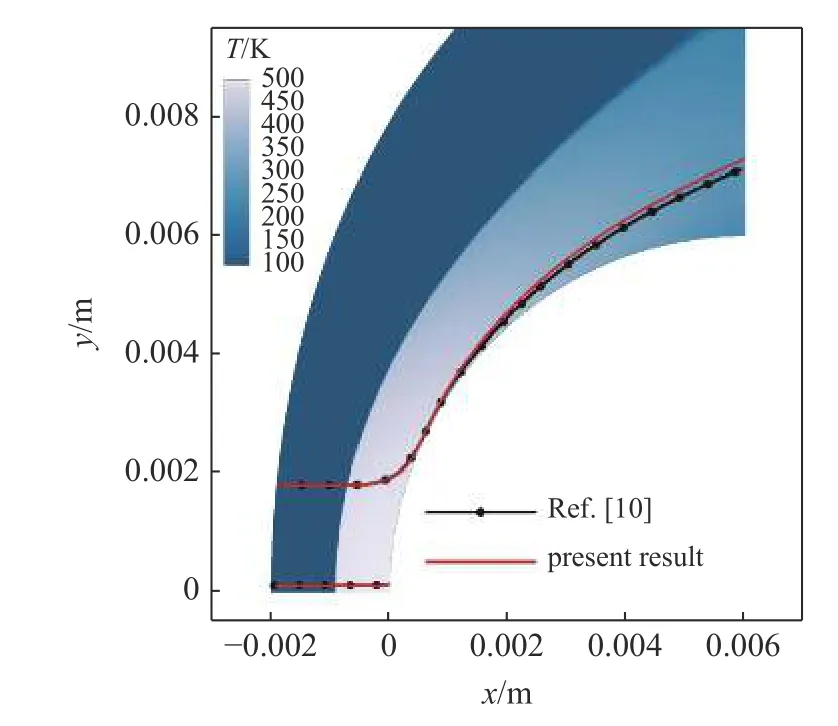
图5 颗粒运动轨迹结果对比Fig.5 Comparison of particle trajectory

通过对比可以发现距驻点线1.8 mm 的颗粒均在到达壁面前受流场影响发生偏转,运动转向并运动至计算域外,而初始位置ds=0.1 mm 的颗粒与壁面发生碰撞;在初始位置ds=1.8 mm 的颗粒轨迹后半段存在一定偏差,这是由于单向耦合下颗粒轨迹计算结果不仅与流场计算结果有关,而且颗粒在流场中的插值方法和颗粒运动的时间步长选择等对计算结果均有影响,而文献[10]中并未包含完整的流场信息、选用的插值方法以及如何确定时间步长;为了对计算结果的偏差进行量化,将计算结果与文献[10]参考数据的纵向差值与颗粒进入激波后的运动轨迹长度的比值设为偏差值Δe,通过计算得ds=1.8 mm,直径dp=0.19 μm 的颗粒在运动轨迹上的最大偏差值Δe=0.73%,在颗粒运动轨迹规律一致的情况下认为该偏差是可以接受的.

3.3 网格无关性与颗粒CFL 敏感性分析

首先,采用3 组不同的网格数目来对本文流场计算进行网格无关性说明,分别为250×180 (第一层壁面网格高度Δn=0.1357 mm),350×180 (Δn=0.0965 mm),450×180 (Δn=0.0744 mm),仅对垂直于壁面方向网格加密.针对本文选取的30 km 高度的自由来流条件,图6 给出了3 种不同网格数目下驻点线上的x方向速度分布以及驻点线上的温度分布,可以看出本文计算结果基本不受网格数量的影响.后续研究中采用350×180 网格量的结果,其中垂直于壁面方向为350 个网格.

图6 网格无关性研究Fig.6 Grid independence studies

不同的颗粒CFL 数会改变计算的时间步长,影响到颗粒运动轨迹的计算,本节对颗粒计算程序的颗粒CFL 数进行敏感性分析,在激波附近区域存在较大的速度梯度与温度梯度,所以当颗粒运动到激波附近时(本文根据密度梯度定义,当颗粒所在网格密度梯度大于5 kg/m4时),将颗粒CFL 数调整为0.01,而远离激波时颗粒CFL 数分别设置为0.1,0.3 和0.5.不同的颗粒CFL 数对应的颗粒轨迹如图7 所示,当颗粒CFL 数在0.1～0.5 范围内时,计算所得颗粒的运动轨迹差异约为流场尺度的0.1%,可以认为颗粒的运动轨迹基本重合,在本文网格尺度下,颗粒CFL 数取为0.3 (激波附近为0.01).

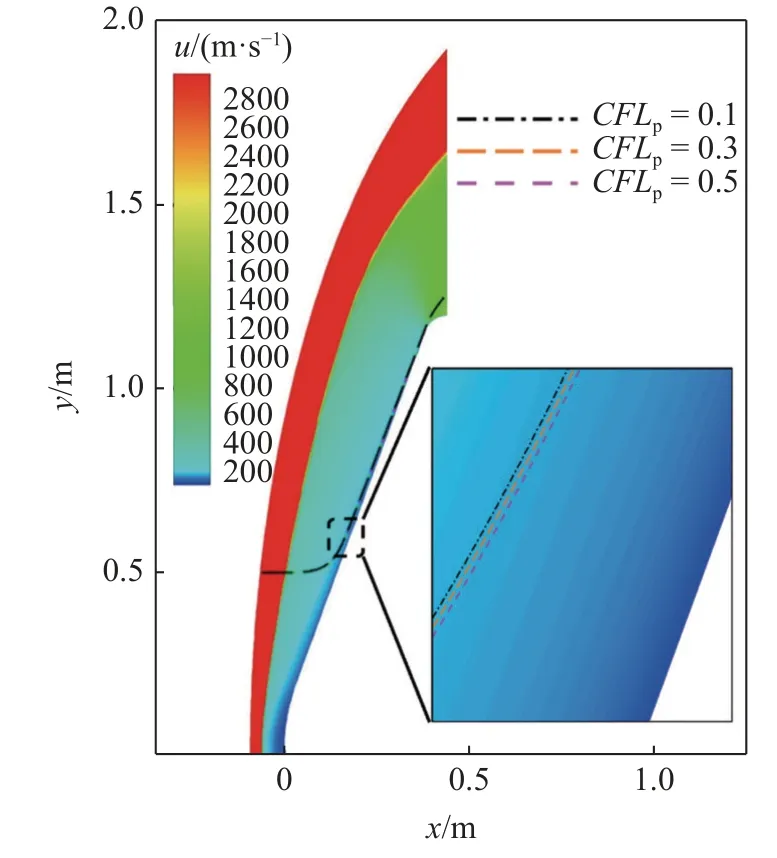
图7 颗粒CFL 数无关性检验Fig.7 Particle CFL number independence test

4 结果与讨论

4.1 颗粒高温相变模型的影响

单向耦合方法下,颗粒在计算域网格入口边界均匀间隔的初始位置生成并添加至稳态的流场中,通过颗粒运动方程进行迭代以及更新颗粒的属性,直到颗粒撞击在壁面或离开计算域停止计算.

颗粒在流场的运动中伴随着热量交换,不同尺寸的颗粒到达其融化温度需要吸收的热量不同,图8中给出的是dp=0.5,1.5 和2.5 μm 的颗粒在不考虑和考虑相变情况下的运动轨迹.

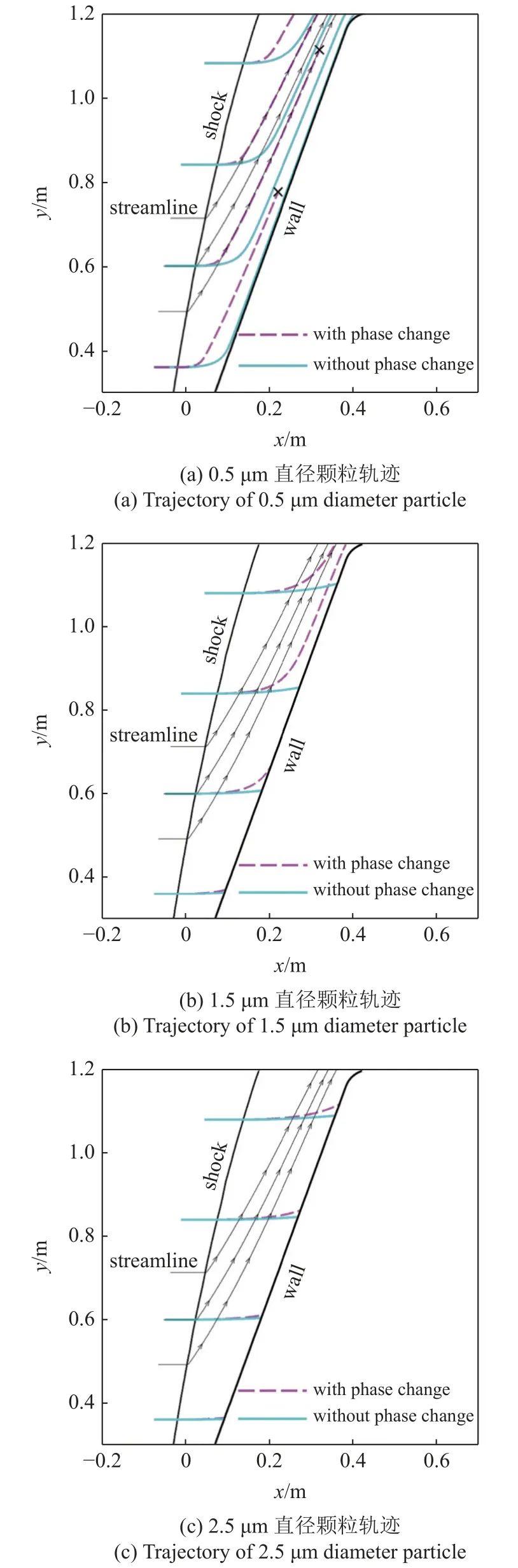
图8 相变模型对颗粒轨迹影响Fig.8 Effect of phase transition model on particle trajectories

根据阻力计算式(1),可得颗粒所受到的加速度为

对于dp=0.5 μm 的颗粒,其粒径小,惯性力小,不考虑温升模型时大部分颗粒均受流场影响发生偏转后,随着流线运动至肩部以外而不与壁面发生撞击,如图8(a)所示;考虑温升模型后,颗粒吸收热量达到熔点,半径减小,根据式(20)可知,颗粒所受加速度与其半径成反比,因此小尺寸的颗粒加速度更大.

在多相流体动力学中,定义斯托克斯数St来衡量粒子跟随性[32],当斯托克斯数很小时,粒子具有足够时间去响应流场的变化,即跟随性越好.St=τp/τt,τt为流动特征时间,τp为颗粒松弛时间或响应时间[33],定义如下

式中,ρp为颗粒密度;dp为颗粒直径;μ为流体的黏性系数;Knd=λ/dp为颗粒克努森数,λ为分子平均自由程.因此dp越小对应的St越小,对应着颗粒的跟随性越好,本文的计算结果也表明小尺寸颗粒展现出相对更好的跟随性;考虑颗粒的高温相变造成小尺寸颗粒体积变化量相比于其原始体积占比更重,运动一定距离后会完全融化甚至蒸发消失(本文判定依据为dp＜ 1.0×10-12m),因此dp=0.5 μm 的颗粒基本不会对壁面侵蚀产生影响;dp=1.5 μm 的颗粒运动轨迹与另外两组直径颗粒受温升影响下轨迹偏离程度相对更大,靠近驻点线的颗粒运动时间相对较短,在其轨迹未发生明显偏转时已撞击在壁面,靠近肩部的颗粒发生相变后粒径减小,加速度相对变大,颗粒响应时间减小,St数逐渐减小,流场跟随性增加,且由于吸收的热量不足以使颗粒融化至消失,其与不考虑温升模型的颗粒轨迹相比差异最大;dp=2.5 μm 的颗粒受温升影响相对较小,主要原因是颗粒自身粒径大,体积大,对应的St数相对较大,跟随性相对较差,且在流场运动中吸收的热量不足以达到其融化温度,因此其运动轨迹变化相对较小.

由上分析可知,高温相变模型对于颗粒运动的影响和其初始位置以及粒径有关;从颗粒对壁面的撞击规律来说,相变模型对于较小或较大的颗粒影响不大,较小颗粒和流动的跟随性较好,较大颗粒的潜热较大,从流场吸收的热量对其运动轨迹影响不大.本文后续的讨论都是考虑有高温相变模型的工况.

4.2 颗粒运动分析

不同粒径的颗粒在流场中运动,其运动轨迹及其对飞行器壁面的侵蚀差异较大,图9 选取直径为1 μm 和5 μm 颗粒作为参考,对不同初始位置的颗粒运动轨迹进行对比分析.

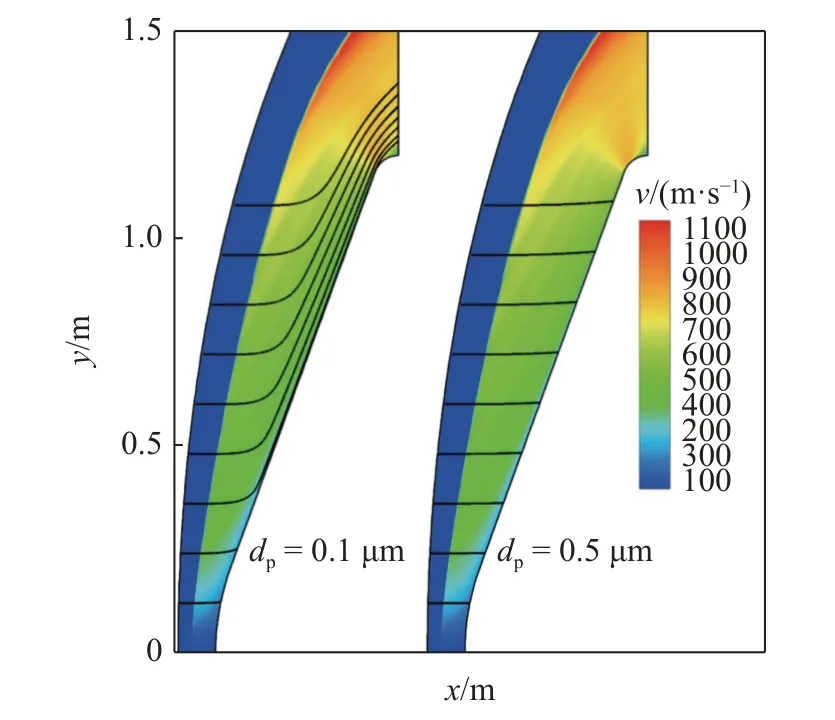
图9 不同直径颗粒轨迹示意图Fig.9 Trajectories of particles with different diameters

对于dp=1 μm,靠近驻点线的颗粒受流场影响较小,由图9 可知,气体经过激波后靠近驻点线处的流场在y方向速度分量νg较小,靠近肩部的νg较大,而颗粒经过激波时速度不受影响,νp为0,此时靠近驻点线处流场与颗粒y方向速度差 Δv较小,

由式(1)可知,y方向速度差 Δv越小表明颗粒受到较小的y方向流场作用力,即颗粒在y方向的加速度越小;此外,在驻点线附近激波脱体距离比较小,气体对颗粒作用时间短.因此,靠近驻点线的颗粒更容易与壁面发生撞击;而靠近肩部的颗粒与流场y方向速度差Δν相对较大,作用时间也相对较长,受流场影响较大,更贴近流线运动;对于dp=5 μm的颗粒,其具有较大的质量和惯性,在流场中受影响较小,基本都以x方向运动为主,最后撞击到壁面.

图10 为在同一初始位置下对不同粒径颗粒轨迹的模拟.根据式(20)计算,ap与rp成反比关系,随着粒径的增大,颗粒受到的加速度变小,即流场对颗粒作用越晚体现,dp=0.5 μm 的颗粒在进入激波后最早在流场作用下出现“转向”现象,且在运动过程中由于吸热完全蒸发;其次是dp=1.0 μm 的颗粒,在流场作用下最终脱离计算域;而对1.5,2.0 和2.5 μm的颗粒流场作用较小,均穿过流场后撞击壁面,颗粒越小,向上偏离的位置越远.

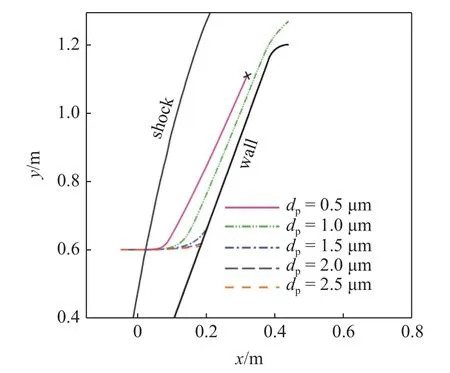
图10 不同粒径轨迹示意图Fig.10 Trajectory of different particle sizes

在飞行器进入的过程中,需要关注的是尘埃颗粒对TPS 的撞击侵蚀,这里引入Connolly 等[34]提出的撞击分数η以及撞击能量分数χ的概念;颗粒撞击分数η被定义为撞击防热罩的颗粒数与基于防热罩半径Anose的截面积上的颗粒总数的比值.受影响的颗粒上游有一个固定的截面积Aimpact,可以利用截面积计算出各尺寸颗粒的撞击分数η

其中,rimpact是能够发生撞击的颗粒在上游径向的最大半径,rnose是防热罩半径,对应图3 中的Rb.

图11 为不同尺寸直径颗粒分别在考虑和不考虑相变模型下进行计算得到的撞击分数对比,由图11可知,无论是否考虑相变模型,直径1 μm 以下的颗粒撞击分数均低于0.1,主要原因是小尺寸颗粒的颗粒响应时间较小,在到达壁面之前大部分均被流场“捕获”运动至计算域以外,另外由于自身体积较小,相变造成颗粒体积变化量相比于其原始体积占比更重,甚至达到融化或完全蒸发的情况,因此并未对TPS 造成侵蚀;而颗粒直径达到3 μm 以上时,其对应的颗粒响应时间比较大,颗粒没有足够的时间响应流场的变化,且由于颗粒自身的体积较大,高温相变模型对其半径的影响较小,因此对应较高的撞击分数.

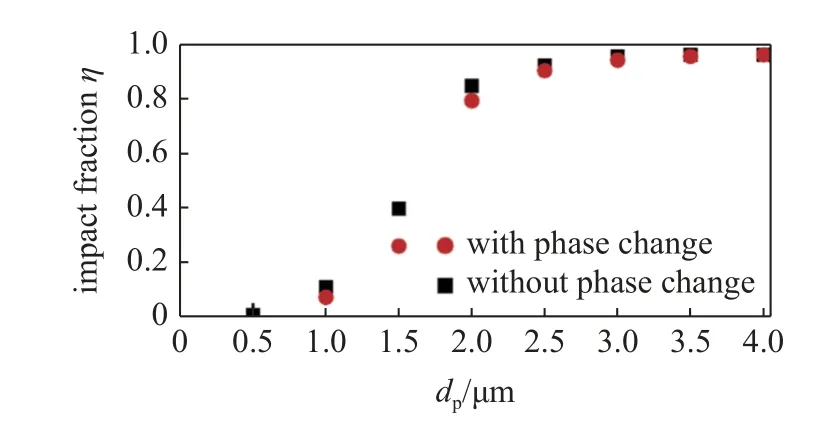
图11 相变模型对撞击分数影响Fig.11 Effect of phase transition model on impact fraction

4.3 颗粒撞击能量研究

对于本文关注的表面侵蚀来说,由于目前没有完善的微尺寸颗粒侵蚀模型,一般认为颗粒对壁面的侵蚀主要与其对壁面造成的撞击能量有关,而颗粒造成的撞击能量主要与它的法向动能有关,其法向动能的损失等于对壁面造成的撞击能量,即

其中,KE⊥是法向动能,mp是颗粒的质量,ν⊥是颗粒撞击壁面时的法向速度.

n个直径相同的颗粒造成的撞击能量可以写为

Palmer 对火星大气尘埃颗粒的大小和数量密度进行了建模,本文选取其提出的模态半径rm=0.35 μm对应的颗粒分布模型,其质量分数分布如图12 所示[9].

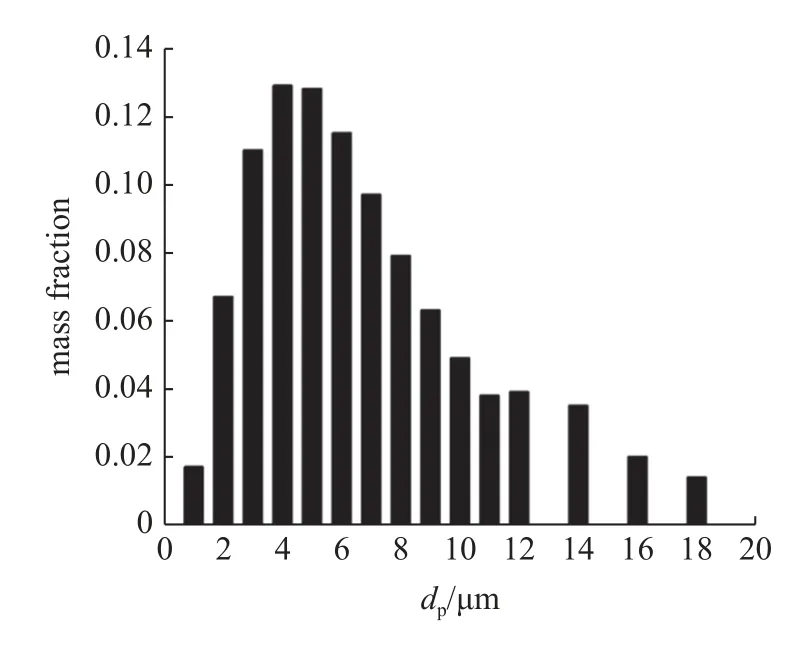
图12 颗粒分布模型[9](rm=0.35 μm)Fig.12 Particle distribution model for rm=0.35 μm

所有尺寸的颗粒造成的总撞击能量为

其中,md是直径为d的颗粒质量,将某特定尺寸直径d的颗粒产生的能量对总撞击能量的占比定义为撞击能量分数χd

图13 为基于本文采用的颗粒分布模型进行模拟得到的撞击能量分数分布.由图可知,平均直径为5 μm 的颗粒造成的撞击能量在该颗粒分布模型所造成的总撞击能量中占比最高,约占13%;对撞击能量主要贡献的颗粒尺寸集中在3～10 μm,约占总撞击能量的80%;由图13 可知,小于3 μm 的颗粒对应相对较小的撞击分数,且由于自身质量较小,撞击在壁面产生的撞击能量较小;直径10 μm 以上的颗粒虽然具有较大的撞击分数以及单个颗粒造成较高的撞击能量,但由于其较小的质量分数,对应较小的净质量浓度,因此直径小于3 μm 或在10 μm 以上的颗粒在撞击能量中占比并不高.

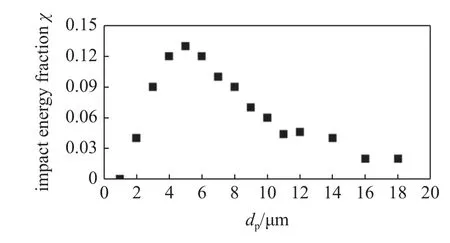
图13 撞击能量分数分布Fig.13 Impact energy fraction distribution

5 结论

本文通过数值模拟方法研究了ExoMars Schiaparelli太空舱在火星大气30 km 高度的来流条件下,大气中微尘颗粒的运动轨迹;同时研究了在给定含尘颗粒质量分数模型下,不同尺寸颗粒对应的撞击分数以及撞击能量分数.本文得出结论如下.

(1) 引入高温相变模型对不同尺寸的颗粒有不同的影响,直径小于0.5 μm 的颗粒由于其体积小,易达到融化温度直至完全蒸发消失;对于直径为1.5 μm的颗粒,颗粒在吸热后发生相变粒径减小,高温相变模型对其运动轨迹影响较大;直径大于 2.5 μm 的颗粒由于体积较大,吸收的热量不足以发生相变,高温相变模型对运动轨迹影响非常小.

(2) 直径1 μm 以下的颗粒跟随性相对较强,对应的撞击分数接近于0,即大部分颗粒不会与模型壁面发生碰撞;颗粒直径3 μm 以上时,其撞击分数达95%以上,即几乎所有初始位置的颗粒全部会撞击到模型壁面.

(3) 考虑颗粒的撞击能量主要与其法向动能有关,直径在3～10 μm 之间的颗粒是壁面侵蚀的主要来源,其造成的撞击能量约占总撞击能量的80%.