基于虚功率原理的鲹科鱼类波状推进分析1)

黄恺俊 余永亮

(中国科学院大学生物运动力学实验室,北京 100049)

引言

自然界中的大多数鱼类进化出波状摆动的方式实现推进[1-3],其中振幅包络线从前部到后部逐渐增加的波状摆动更有利于产生推力[4],这类波动模式通常被称为鲹科模式.鲹科模式与鳗鲡模式、金枪鱼模式都是通过身体和尾鳍的摆动进行推进的,鲹科模式的鱼体前 1/3不波动,后体摆动的波幅随体长增大[3],常见的斑马鱼、草鱼、鲤鱼等都采用这类推进模式.鳗鲡模式的鱼类全部鱼体都大幅摆动,而金枪鱼模式的鱼体仅尾部往复摆动.鲹科鱼类的游速较高,常被用于水下仿生航行器的仿生设计中.因此,深入研究鲹科模式推进的流体力学机制不仅可以增强对波状推进的认识,还可以为水下航行器的设计提供参考.

Videler[2]和Lighthill[5]预测了鱼尾摆动后的流场尾迹,描述波状推进的鱼类在尾部会脱落出交错排列的离散尾涡,被称为反卡门涡街.前人通过数字粒子图像测速仪(DPIV)观测到太阳鱼的尾迹中存在交替的涡结构[6-8],在振荡翼的模型实验中也发现相同的流动[9-11];通过对二维波状翼型的数值模拟,Dong 等[12]、Deng 等[13]和Liu 等[14]也同样观察到这种典型的尾迹结构.与阻力型的卡门涡街不同,反卡门涡街是一种推力型的尾流结构.Yu 等[15]基于波状推进的鱼体产生反卡门涡街的共性,利用涡动力学分析方法,推导并提出了统一描述波状推进的水动力与运动参数、雷诺数的关联关系的标度律.该规律对鳗鲡模式、鲹科模式以及金枪鱼模式都适用.

在研究鱼体运动与受力关系方面,近10 年来也有不少实验和计算分析的工作.Gazzola 等[16]结合实验和数值模拟的结果,通过流体力中推、阻力的匹配关系,得到巡游速度的标度律.Thekkethil 等[17]使用统一的运动学模型进行二维数值模拟,该模型涵盖各种鱼体波动和鱼尾刚体俯仰运动,并研究了波动和俯仰运动的等价性以及推力产生的机制.Hu 等[18]对鱼体的低频波状摆动进行数值模拟,获得鱼体阻力与波动参数之间的标度律.Gupta 等[19]则不光给出波动鱼体受力,还研究了输出功率、效率的标度律关系.Gao 等[20]在Yu 等[15]的工作基础上,基于压差力标度律和摩阻力标度律的匹配关系,也给出巡游速度的标度律.这些工作很好地给出运动与水动力性能的宏观联系,为进一步分析推进的流体力学机制提供数据支持.

事实上,通过计算手段获得流场数据只是全面了解流动的第一步,为了找到流动和受力的定量关系,引入气动力理论的方法可以从流动数据中提取物理规律[21].目前有两种方法可以建立起物体所受力与流场结构之间的联系.一种是Burgers[22],Lighthill[23]和Wu[24]提出的导数矩的方法,通过流体的涡量一阶矩计算流场动量,并通过动量变化求得物体受力.后来被Wu 等[25]发展到有限域的涡量矩理论.另一种是Quartapelle 等[26]、Howe[27]和Chang[28]采用的投影法,通过引入一个势函数,将力分解为附加质量力,兰姆矢量相关的旋涡贡献,以及黏性相关的项.Yu[29]引入虚速度的概念,通过变分得到了流体力学中的虚功率原理,并指出引入的势函数实际上是物体虚运动引起的虚速度场,虚速度场具有远场衰减的特性,在受力分解中包含物面积分项和流体结构的体积分项,并分析各项的伽利略不变形式.为了研究鲹科模式波状推进的流体动力响应,从虚功率原理出发,可以深入分析变形体的边界瞬时流体力效应和流场结构对流体力的贡献.

本文选取鲹科模式推进的鱼体作为研究对象,研究鱼游波状推进的流体力机理.第1 节介绍鱼体波动模型以及基于虚功率原理的分析方法.第2 节通过研究典型参数下鲹科鱼波状摆动流体力的分解来阐明推力的主要来源,然后讨论不同雷诺数条件下推力与Strouhal 数的关系,并结合波状推进的标度律分析,研究标度律公式中各项物理意义.

1 计算模型与分析方法

1.1 鱼游模型

借鉴前人[12,17,19,30]研究鲹科模式鱼类游泳的物理模型,本文采用NACA0012 翼型来模拟鱼体,翼型的中线代表了鱼体在静态平衡时的脊柱.鱼体脊柱波动的侧向位移y(x,t)由Videler 等[31]通过实验提供的行波方程来模拟

其中,λ和c分别表示波动波长和波速,波速是频率f与波长 λ的乘积.如图1 所示,鱼体静止时,头部位于x=0,尾部在x=L处.Am(x)表示不同身体位置的最大振幅.

图1 仿鱼翼型波状摆动示意图Fig.1 Schematic of a fish-like undulatory airfoil

对于鲹科模式的波动,通常认为波长 λ等于一倍体长,身体的振幅包络线Am(x)可由二次函数给出

其中Am(0)=0.02L,Am(0.2)=0.01L,Am(1)=0.1L.图2给出包络线示意图(虚线)和鱼体中线的侧向位移波动曲线(实线),可以看出,最大振幅出现在尾尖处,而最小振幅大概在 0.23L处.鱼体头部有小幅的波动,而尾部相对于头部有更高的振幅.本文定义鱼体尾部最大振幅为鱼体波动的振幅,即波动振幅A=0.1L.

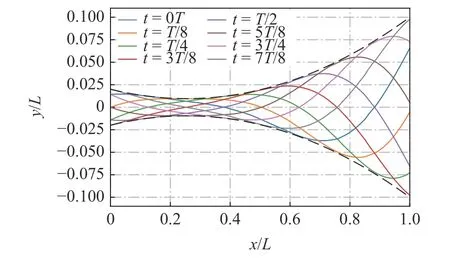
图2 一个波动周期不同时刻的鱼体中心线及其包络线Fig.2 The centerline of the fish body at various time instants for one undulation cycle and their envelops

在本文中,由波动鱼模型引起的二维非定常流动,可由以下无量纲化的不可压缩Navier-Stokes (N-S)方程控制

其中,u是速度场,p是压强场,μ为流体介质的黏性系数.本文选取特征的参考速度U(来流速度),鱼体的体长L以及流体密度 ρ对所有的物理量进行无量纲化,则体现流场惯性力和黏性力比值大小的雷诺数为Re=ρUL/μ.另一个常用的无量纲数是Strouhal数,它表征了流动的非定常性,定义为St=2f A/U.本文采用的数值求解N-S 方程的程序是开源程序包OpenFOAM 的pimpleFoam 求解器,程序的验证和确认见附录,该程序在文献[15]中已得到了验证.

1.2 基于虚功率原理的推力分析方法

通过数值手段获得鱼体波状摆动的流场信息,便可通过鱼体表面的法向应力pn和切向应力 τ=μn×ω积分,得到鱼体的受力F

其中,法向量n指流体的外法向量,和鱼体表面的外法向量方向相反.该公式简洁地给出鱼体与流体的相互作用结果,可用于验证以下基于虚功率原理的推力分析方法.

为了建立流动与受力的定量联系,本文引入Yu[29]提出的虚功率原理的分析方法.假定鱼体在前进方向上产生瞬时的虚运动,则流场中的虚功率关系可得

其中,u*是由鱼体虚运动引起的虚速度场,σji代表施加在流体微团上的表面力的张量(称为应力张量).式(5)的物理意义是物体所受水动力沿着虚运动方向所做的虚功率等于流场中的内应力和广义力的虚功率.广义力包含流场中的体积力fi和惯性力 dui/dt.进一步地,方程(5)左侧的值就是推力FT,即水动力沿着虚运动方向的分量,所以对方程(5)右侧各项的分析将有助于理解推力的物理成因.

Yu[29]在文中提到,可以假定虚流场是不可压缩势流.为了使势函数唯一,采用了在无穷远处势函数φ为0 的边界条件[26,28-29].因此,虚流场满足的方程和边界条件如下

其中 ∇ φ是虚流场的速度矢量u*,Sfish和S∞分别表示鱼体表面和无穷远边界.虚流场是无源无旋的,可通过在鱼体表面分布基本解(源汇和偶极子)以满足方程(6)的鱼体和无穷远处的边界条件.将虚流场方程(6)代入虚功率关系(5),并考虑流动不可压缩且体积力可忽略,则表达式(5)右式的两项分别为

从式(7)可以看出流场的流体内应力对虚应变做功的功率转换为壁面的切应力 τ所做的虚功率,一部分是对虚速度场做功的功率,另一部分是对鱼体虚运动做功的功率.前者被称为类摩阻(该说法来自Chang[28]),后者正好为摩阻在推进方向的大小.从式(8)可以看出流场中惯性力的虚功率可以转换为与鱼体边界加速度有关的表面积分和与流场中对流散度有关的体积分.表面积分表明壁面的瞬时运动即可确定部分虚功率的大小,其值可以看作在黏性流动中鱼体运动状态瞬时所确定的推力贡献.而流体对流的散度正好等于负的2 倍Q(Q是速度梯度张量的第二不变量,定义为Q=0.5(||Ω||2-||D||2),其中 Ω 和D分别是速度梯度分解成的反对称张量和对称张量),Q＞0代表流体质点的旋转强于应变速率,Hunt 等[32]就提出用Q＞0作为旋涡的识别.因此,式(8)中右边第二项可以看作是流场中流体的旋转和应变速率相对大小对推力的贡献,为了方便,我们称之为Q贡献.

因此,本文将鱼体受到的推力FT分解为4 个分量

分别表示边界加速度对推力的贡献FT,a、流场中Q对推力的贡献FT,Q、边界的类摩阻分量FT,v以及摩阻分量FT,f,其推力系数及各分量的系数定义为

2 结果与讨论

2.1 典型问题的推力分解

为了考察式(9)受力分解与式(4)在推力分析上的一致性,选择无量纲摆尾幅度为A=0.10,波长为 λ=1.0,波速为c=2.0,流动的雷诺数为Re=5000

作为典型的案例,对比了一个摆动周期里推力系数随时间的变化,如图3(a)所示.结果表明基于虚功率原理的推力曲线与由式(4)直接积分的推力曲线重合,具有一致性.进一步地,图3(b)给出了4 个分量CT,a,CT,Q,CT,v和CT,f随着时间变化的曲线,发现边界加速度对推力始终是一个正的贡献,而流场中Q对推力有很大的负贡献,两者相位几乎相反.边界的类摩阻分量相对于其他分量要小得多,几乎可以忽略不计,而摩阻分量在一个周期内始终是阻力.四者的周期均值分别为 0.2474,-0.1192,0.0003和-0.0607,可见CT,v的确可以忽略,推力主要由CT,a,CT,Q,CT,f3 项组成,其中CT,Q接近摩阻CT,f的两倍.接下来我们将对推力贡献最重要的两部分CT,a和CT,Q做进一步的分析.

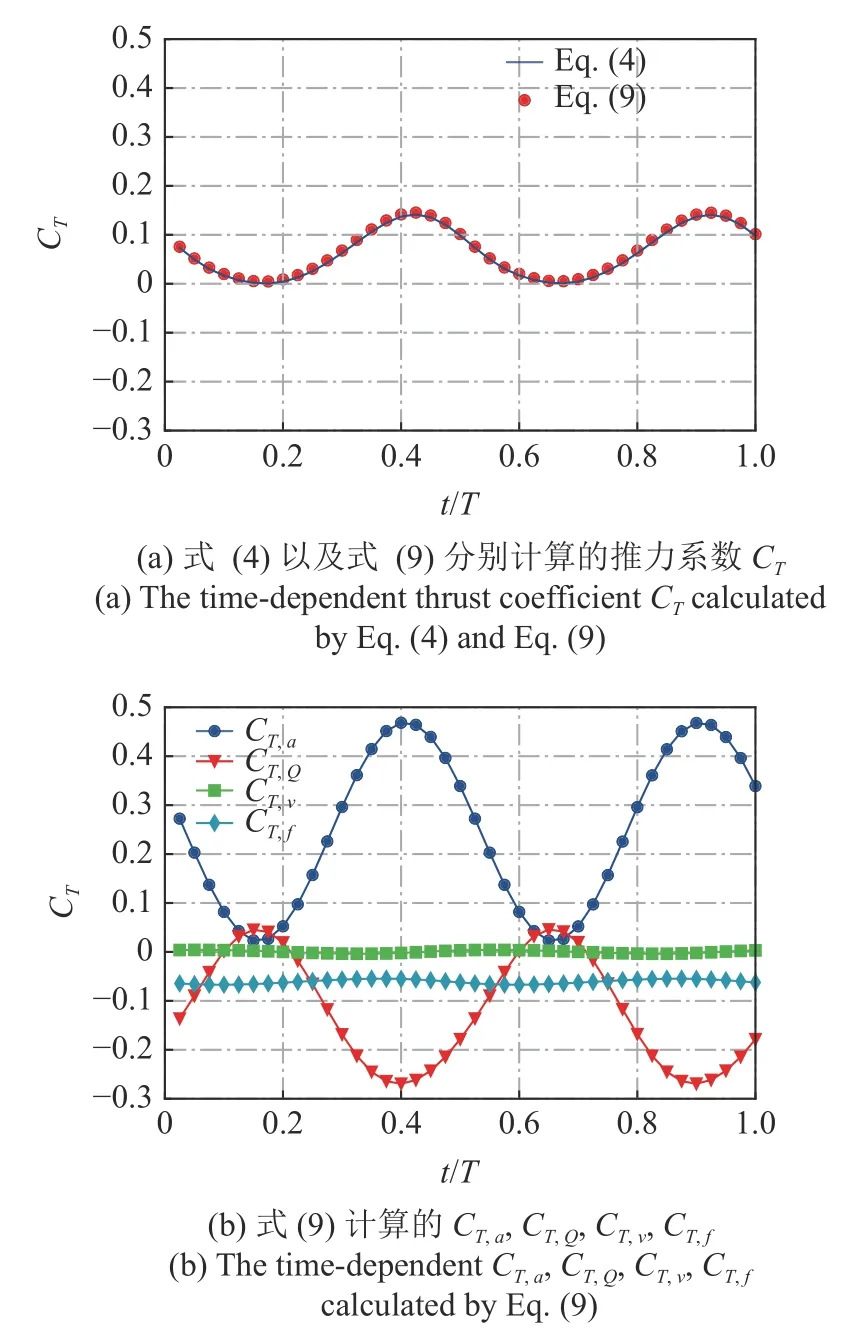
图3 推力系数在一个周期内的变化Fig.3 The time-dependent thrust coefficient in an undulation cycle

对于二维波动模型,可以对边界加速度对推力的贡献FT,a做进一步的推导.分别沿着上、下表面进行积分可以得到

其中,下标+和下标-分别代表上下表面的物理量,y+和y-分别代表上下表面的曲线方程,y′=∂y/∂x代表曲线对x的导数.根据变形规则,在相同的x坐标,鱼体边界与鱼体脊柱波动一致,则边界加速度的值du/dt是相同的.边界加速度可由波动方程对时间的二阶导数获得,流体在鱼体表面的外法向量可由曲线方程获得,具体关系如下

将方程(12)代入方程(11),我们可以得到

基于式(13)我们可以看出由边界加速度引起的推力贡献沿着鱼体中线的分布与两部分相关因素相关.一部分是侧向运动的y方向加速度(波动加速度),另一部分是上下表面的虚速度势的差值.根据势流的特点,鱼体表面的虚速度势是由当前时刻的鱼体外形决定的,因此

图4(a)给出了一个摆尾周期内边界加速度对推力贡献沿着中线的分布,其中实线和点被用来区分摆尾前半周期和后半周期的特定时刻.从图4 中可以看出,前半周期和后半周期的摆尾动作产生的FT,a是一致的.从曲线看,头部区域由于变形小,加速度小,对FT,a的影响就小,尾部区域的值波动大,大部分时刻都处于正值,这意味着对推力有大贡献.进一步地,为了更好地展示鱼体各个部位变速运动带来的贡献,将鱼体沿中线等分成5 个区域,并统计了5 个区域分别对推力贡献的周期均值,如图4(b)所示.从数据上可以看出,前3 个区域的均值与整体均值之比大约为3%～4%,且均为负贡献,处于尾部的第4 和第5 区对整体正推力有很大的正贡献,特别是加速度最大的第5 区,虽然只占鱼体长度的20%,但这个区域的贡献占整个贡献的83.25%.

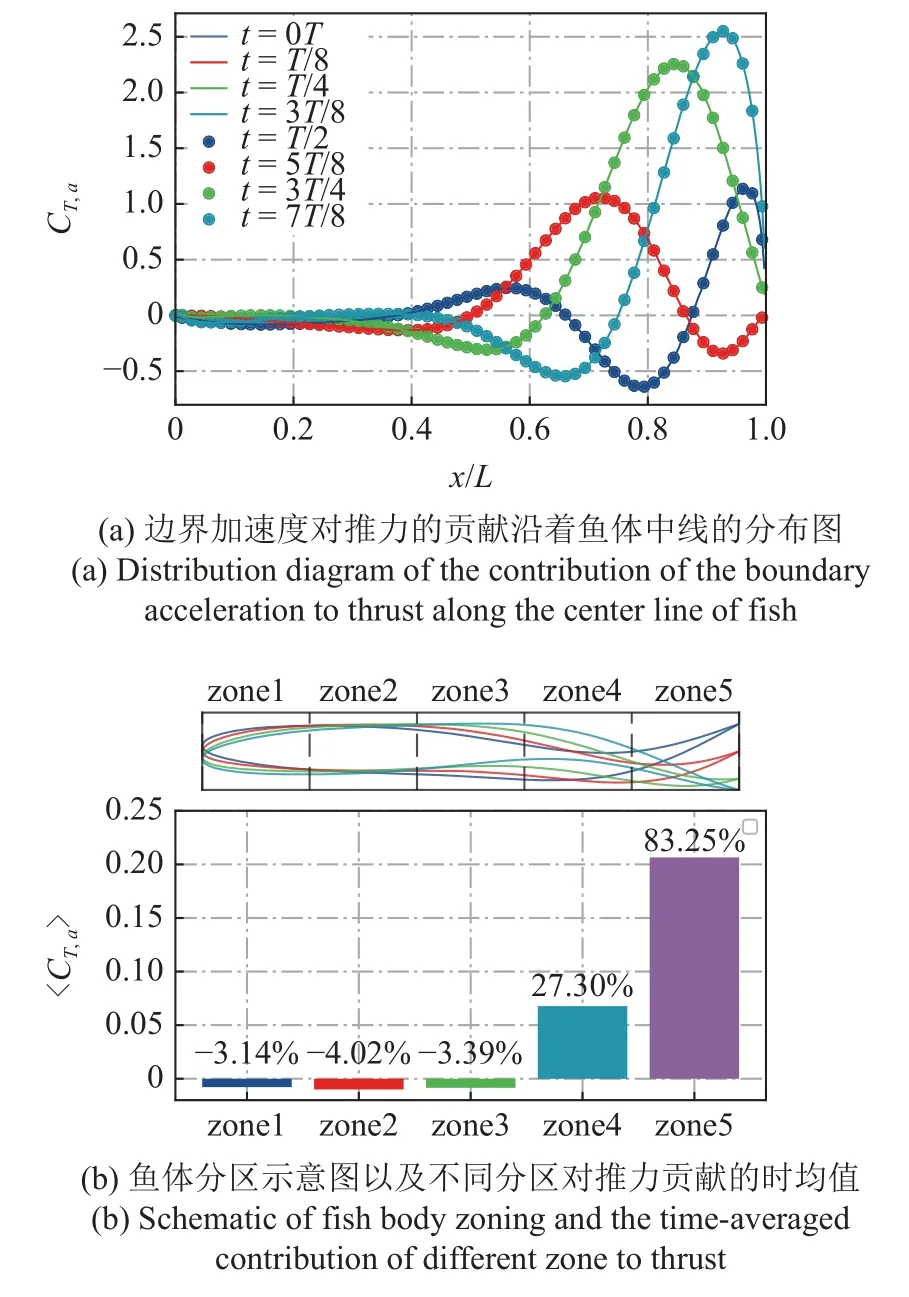
图4 边界加速度对推力的贡献Fig.4 The contribution of the boundary acceleration

根据式(9)右式第二项可知,流场中的Q分布对推力的贡献依赖两个因素,一个是Q的强度,另一个是虚速度势 φ.为了更好地展现流场信息,图5 给出了4 个典型时刻的流场涡量分布、Q值分布、Q对推力贡献分布,以及虚速度势的分布.从涡量场来看,鱼体上半部分边界层内为负涡量,下半部分为正涡量,尾迹呈现典型的反卡门涡街结构.从Q值图上可以看出,在鱼体上下部分的边界层处,Q值仅在尾部附近有明显的分布值,且两侧的值相反,意味着尾部拍动的过程中,“迎风面”(图中显示的鱼体尾部下表面)边界层内的流体应变速率强于旋转(Q＜0),而另一侧的尾部附近流体的旋转强于应变速率(Q＞0).在鱼体头部,存在很强的应变速率区(Q＜0),头部两侧后方存在很强的旋转区(Q＞0).对于脱落到流场中的自由旋涡,无论是正涡还是负涡,中心都由流体旋转主导(Q＞0),且在旋涡周围存在较弱的应变速率区(Q＜0).随着鱼体的摆动,虚流场的速度势函数 φ也会随之变化,特别是在尾部区域,鱼体外形变化大导致 φ值变化大.流场中流体的旋转和应变速率的相对大小对推力的贡献(-2ρQφ) 在头部区域有正有负,在尾部边界层区域也有正有负.在尾迹区,由于虚速度势始终为正(φ ＞0),故脱落出去的旋涡中心贡献了负推力,旋涡周围呈现一个较弱的正贡献.

图5 t=0T,t=T/8,t=T/4,t=3T/8 时刻的涡量场(第1 列)、Q 分布图(第2 列)、Q 对推力的贡献分布图(第3 列)和虚速度势场(第4 列)Fig.5 Vorticity field (first column),Q distribution diagram (second column),Q distribution diagram of contribution to thrust (third column) andvirtual velocity potential field φ (fourth column) at t=0T,t=T/8,t=T/4,t=3T/8

为了更好地定量展示流动结构对推力的贡献,我们基于流场中Q分布的特点,人为对整个流场进行了分区.如图6 所示,zone0 代表了距离鱼头部一定距离的流场,该区域的Q值都很小.zone1 是鱼体头部附近的区域,其Q分布有正有负.zone2～zone5 分别代表身体波动的部分,且波动的振幅逐渐增强,这些区域分布的Q强度也逐渐增强.区域zone_wake 则是尾迹区,该区域又被分为对应的5 个子区,由近及远分别为wake1～wake5.

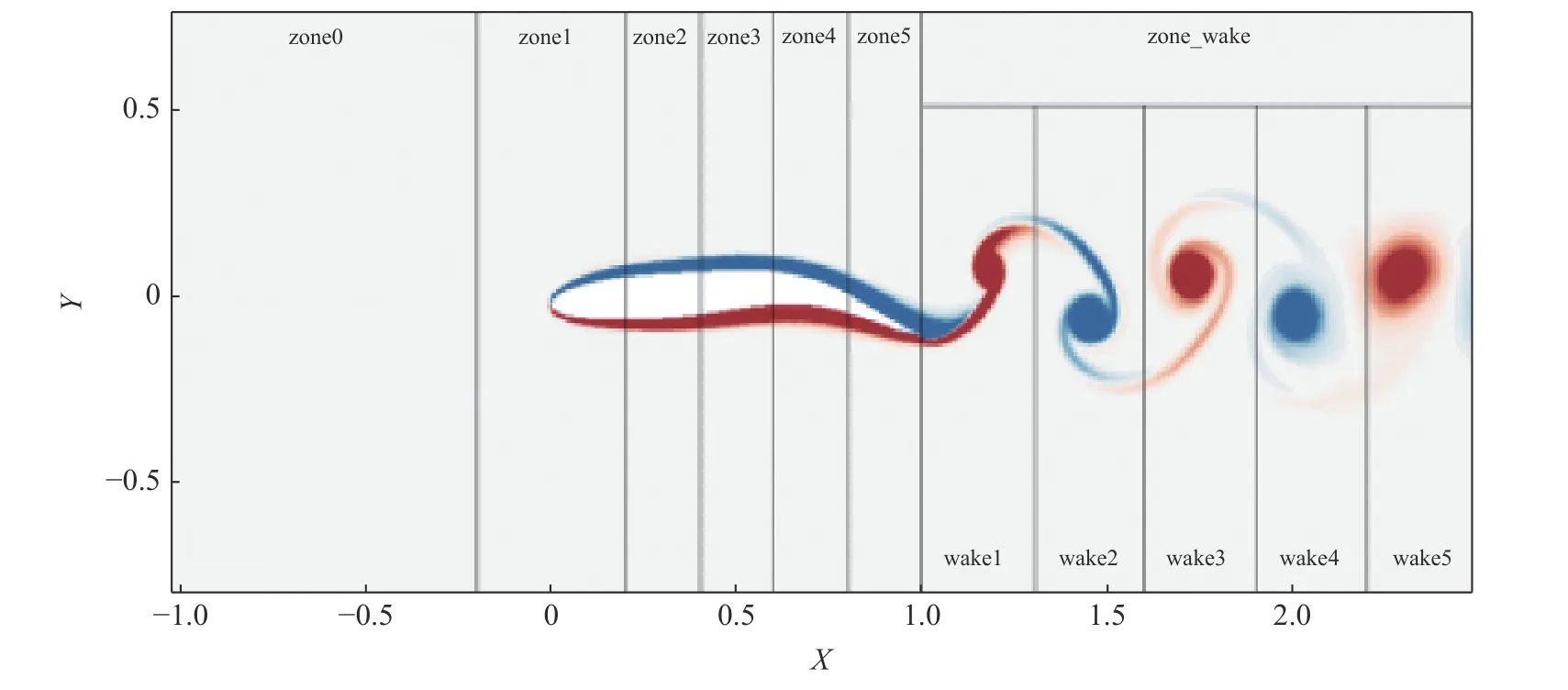
图6 流场分区示意图Fig.6 Schematic of flow field zoning

图7(a)给出了各个分区Q分布对推力的贡献随着时间变化的曲线,图7(b)给出了各个分区对推力贡献的周期均值,它们具有如下几个特点.(1)从时变曲线来看,zone0 和zone1 的推力贡献值都在零附近小幅振荡.由于zone0 区的流场扰动小,Q值小,整体流动几乎没有推力贡献.zone1 的头部区存在强正强负的贡献,但整个摆动周期中变化小,其贡献也较小.(2)鱼体波动的zone2～zone5 这4 个区因摆动振幅逐渐增大而对推力贡献值也波动增强.其中,zone2,zone3 和zone4 的波动曲线仍在零值附近振荡,从均值来看,zone2 和zone3 区域对推力有贡献,但zone4 区呈现出阻力特性.zone5 是鱼体尾尖附近的区域,振荡最强,其周期均值最大,具有大阻力特征.(3)尾迹区在摆动中大部分时间里都呈较弱的振荡,其周期均值为 9.31%,体现的是阻力,远小于zone5的作用.由此可见,流场中的流动结构带来的阻力振荡也主要来自于尾部附近.

图7 Q 分布对推力的贡献Fig.7 The contribution of Q distribution to thrust

为了更好地展示尾迹区的旋涡贡献,图8 给出了尾流区(wake1～wake5)的Q对推力贡献随时间的变化.结果表明,每一个分区对推力的贡献都是负的,越远离鱼尾的尾迹区域,曲线的涨落就越小,均值也越小.曲线的涨落主要是由于旋涡在区域内流进流出引起的,而远离鱼体的尾迹区的均值减小是由于虚速度势函数是随距离的衰减函数.整体来看,尾迹区对鱼体受力的影响是较弱的.

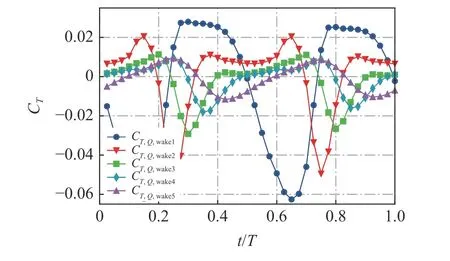
图8 不同尾迹区的 Q 分布对推力的贡献Fig.8 The time-dependent contribution of Q distribution to thrust in different wake regions

本小节讨论了典型波状推进情况下的流体力分解.研究发现,鱼体波状摆动产生的推进力,其正贡献主要来自于边界加速度的瞬时响应,而流场中的流体旋转和应变速率相对大小对应的是阻力,在鲹科类的摆尾推进中,两者都主要体现在尾部附近的流动.除此之外,边界上的黏性耗散效应主要体现在摩阻上.

2.2 推力与St 数关系

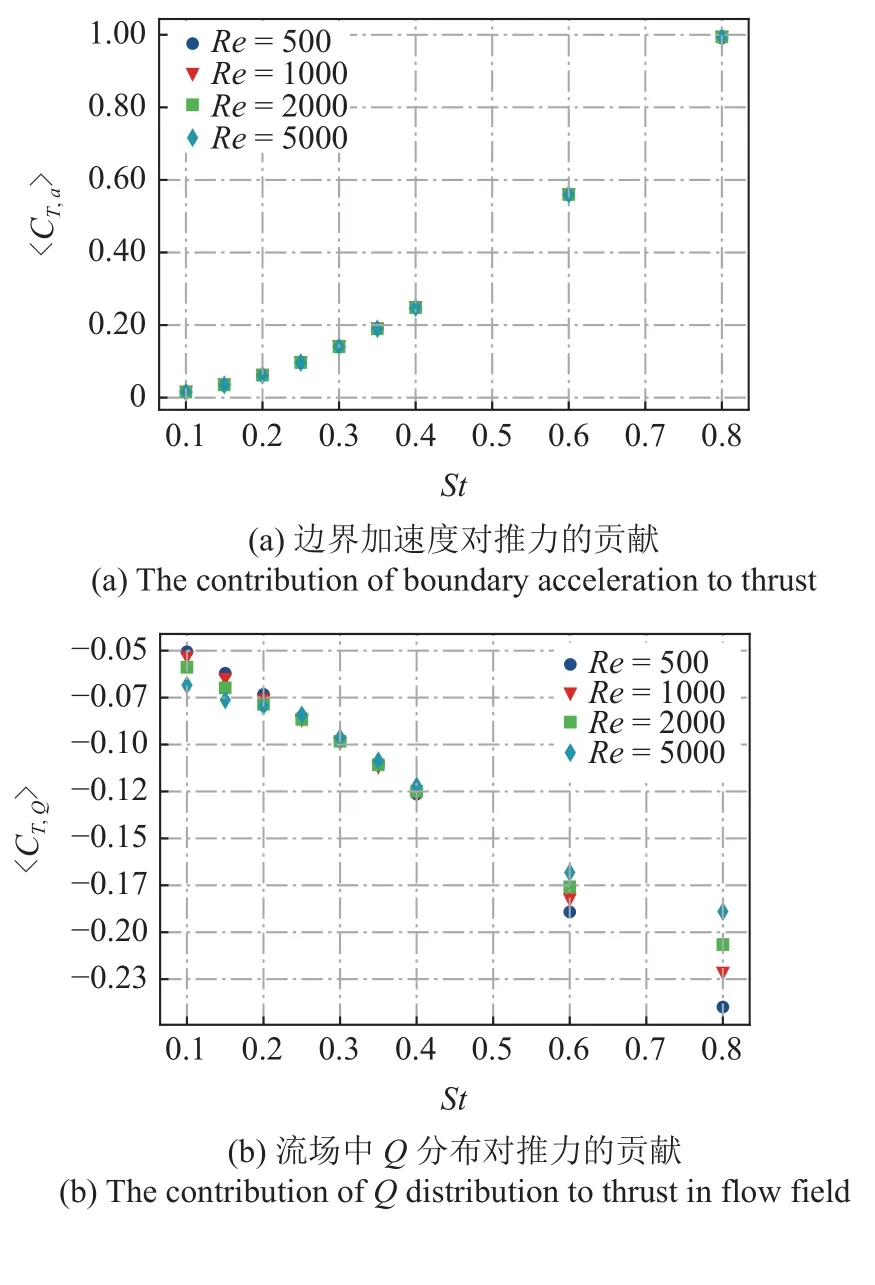
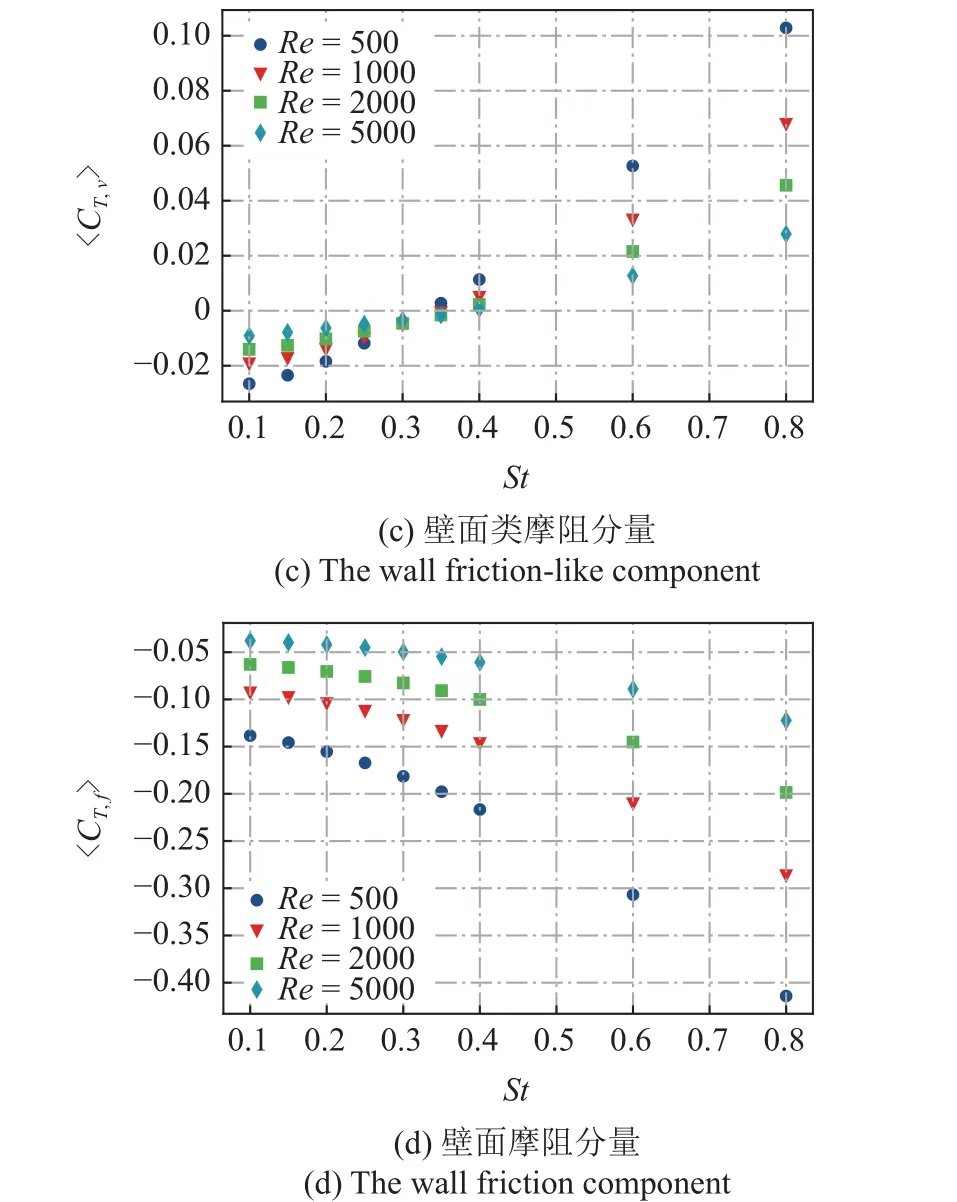
图9 不同雷诺数Re条件下,〈CT,a〉,〈CT,Q〉,〈CT,v〉和〈CT,f〉 随运动参数St的变化规律Fig.9 The time-averaged thrust coefficient 〈CT,a〉,〈CT,Q〉,〈CT,v〉,〈CT,f〉 as a function of St at different Reynolds number

为了更好地显示4 部分时均值对推力贡献的相对大小,图10 给出了Re=500 和Re=5000情况下的各项贡献的堆叠柱状图.从图中可以看出,无论是低雷诺数还是高雷诺数情况,正推力的贡献都主要来自于边界变速运动.壁面切应力的类摩阻分量无论产生正贡献还是负贡献,相对于其他3 项总是较小的.阻力分量主要来源于流场中Q的贡献和壁面摩阻的贡献.对于低雷诺数(Re=500)的情况,两者的阻力贡献相当,摩阻的阻力贡献略大于流场中Q的贡献.对于高雷诺数(Re=5000) 的情况,流体中Q分布的阻力贡献强于摩阻的贡献.

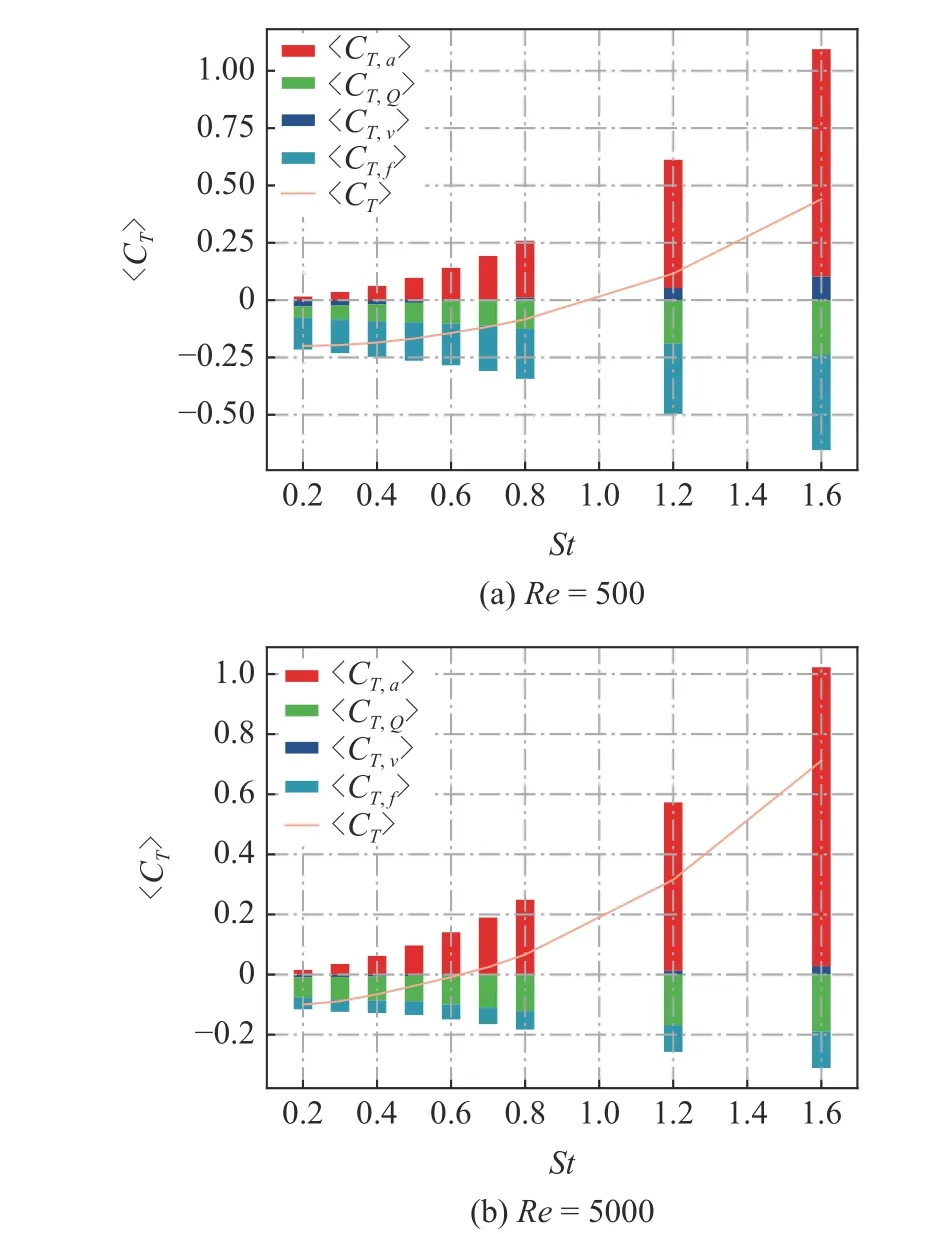
图10 不同雷诺数Re条件下,〈CT,a〉,〈CT,Q〉,〈CT,v〉和〈CT,f〉的贡献堆叠柱状图Fig.10 Stacked histogram of the time-averaged thrust coefficient 〈CT,a〉,〈CT,Q〉,〈CT,v〉,〈CT,f〉 at different Reynolds number

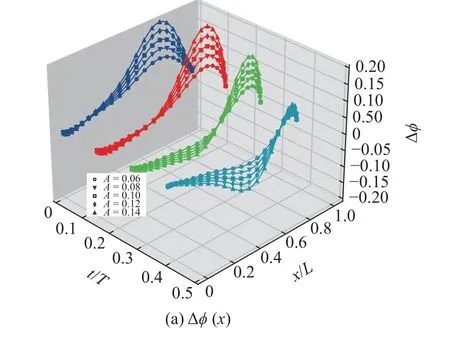
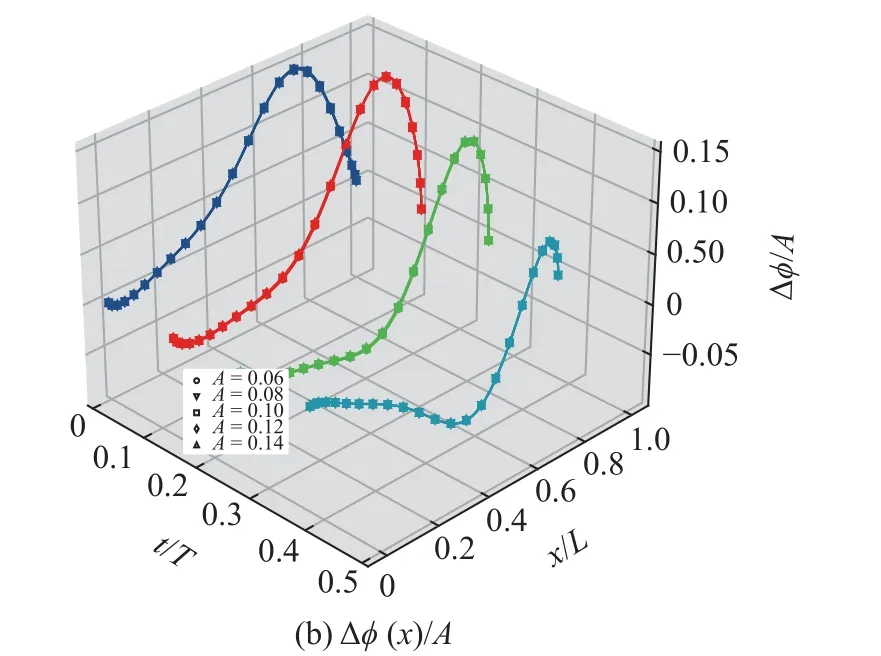
图11 在 t=0T,t=T/8,t=T/4和t=3T/8 时刻以及不同摆幅条件下(A=0.06,0.08,0.10,0.12,0.14),Δφ(x) 以及 Δφ(x)/A 沿着鱼体中线的分布Fig.11 Distribution of Δφ(x) and Δφ(x)/A along the center line of fish at different time (t=0T,t=T/8,t=T/4,t=3T/8) and under different amplitude condition (A=0.06,0.08,0.10,0.12,0.14)

曲线几乎重合,这表明 Δφ(x)与摆幅A成正比,即,Δφ(x)∝A.

因此,对于任意时刻,FT,a沿着鱼体中线的分布都与A2f2成正比,由此可得

即由边界加速度得到的瞬时推力和推力均值都与S t2成正比,并且图4(b)给出的分区贡献占比不会随着运动参数S t的变化而变化.

进一步关于时均值 〈CT,a〉,〈CT,Q〉,〈CT,v〉和〈CT,f〉的分析可以结合已经发表的关于鱼体波状推进标度律[15]进行分析.

2.3 波状推进的标度律分析

Yu 等[15]基于涡动力学分析方法,给出了仿鱼类波状摆动推进器的推力系数与S t和Re之间的标度关系,即

图12 惯性力对推力贡献的标度关系及其拟合参数与雷诺数的关系Fig.12 Scaling law of the contribution of the inertial force to thrust and the relationship between fitting parameters and Reynolds number

图13 内应力对推力贡献的标度关系及其拟合参数与雷诺数的关系Fig.13 Scaling law of the contribution of the internal stress to thrust and the relationship between fitting parameters and Reynolds number

3 结论

为了研究鲹科鱼类的推进与流场结构的关系,基于虚功率原理,将推力分解为鱼体边界变速运动的贡献FT,a、流场中流体旋转和应变速率相对大小的贡献FT,Q、壁面剪切应力的类摩阻分量FT,v和壁面摩阻分量FT,f.除了流体旋转和应变速率相对大小对推力的贡献是流场体积分外,其余3 个推力分量均为鱼体表面积分,而壁面加速度对推力的贡献是由鱼体运动瞬时决定的.

通过对鲹科鱼类波动的二维模型的推进分析,结果显示推力主要来源于鱼体边界变速运动的贡献,它是黏性流动中流体对鱼体波动的瞬时反作用力,而流场中流体旋转和应变速率相对大小的贡献(时均值)总是负的,它们是推力组成的主要两个部分.从流场分区来看,推力主要来源也是鱼尾的变速运动和鱼尾边界层的流动,而流场尾迹的旋涡对推力的影响较小,距离越远影响越小.

进一步研究表明,推力分解的4 个量均与表征非定常性的Strouhal 数呈二次关系;边界变速运动对推力的时均贡献与雷诺数无关,其余3 个量均受雷诺数影响.结合标度律分析后发现,流场中流体的旋转和应变速率相对大小对推力的贡献也有一部分是与雷诺数无关,其与雷诺数有关的摆动标度部分的阻力成分相当于壁面剪切力的类摩阻分量和摩阻分量之和的一半,而类摩阻和摩阻还存在常阻力成分.

总之,基于虚功率原理的鲹科鱼类波状推进分析表明,鱼体的推进力主要依赖尾部的变速运动和尾部两侧的边界层控制,且提高波速和增强摆动速率都可以获得高的推进力.

附录A 数值结果验证

本文基于OpenFOAM 通过有限体积法求解二维非定常不可压缩Navier-Stokes 方程组(方程(3)),采用PIMPLE 算法求解控制方程.PIMPLE 算法是基于SIMPLE 算法和PISO 算法的一种改进算法,在时间步内,通过低松弛稳定计算获得较大的时间步长,在每个时间步内使用PISO 算法对压力进行多次修正使之满足压力速度耦合方程[B1].方程中的时间导数项采用一阶隐式Euler 格式离散,动量方程中的对流项采用Gauss linear upwind 格式进行离散,扩散项采用Gauss linear 格式进行离散.

本文设定的计算域为 16L×8L,网格是使用OpenFOAM自带的网格自动生成工具snappyHex Mesh 生成,鱼体附近的动网格如图A1 所示.本文计算了在 λ=1.0,c=2.0,Re=5000时,推力系数和侧向力系数随时间的变化,如图A2 所示.网格选取了 160×80,480×240 以及 800×400 这3 种情况,时间步长选取了 ΔT=2.5×10-4,ΔT=1.0×10-4以及 ΔT=5.0×10-5.从图A2 中可以清楚地看出,160×80 和 480×240 网格大小的计算结果存在合理的差异,而 480×240 和 800×400 网格大小的差异几乎可以忽略不计.此外,计算结果与Dong 等[12]公布的结果吻合较好.因此,本文中的模拟都使用了 480×240 的中等网格尺寸和时间步长 ΔT=1.0× 10-4,鱼体附近的最小网格高度约为 0.0001.

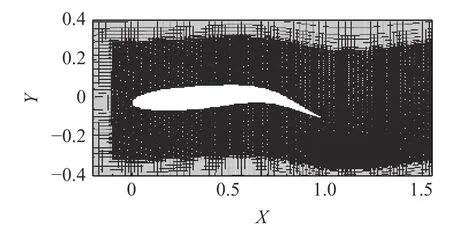
附图 A1 鱼体附近动网格示意图Fig.A1 Schematic of dynamic meshes near fish body

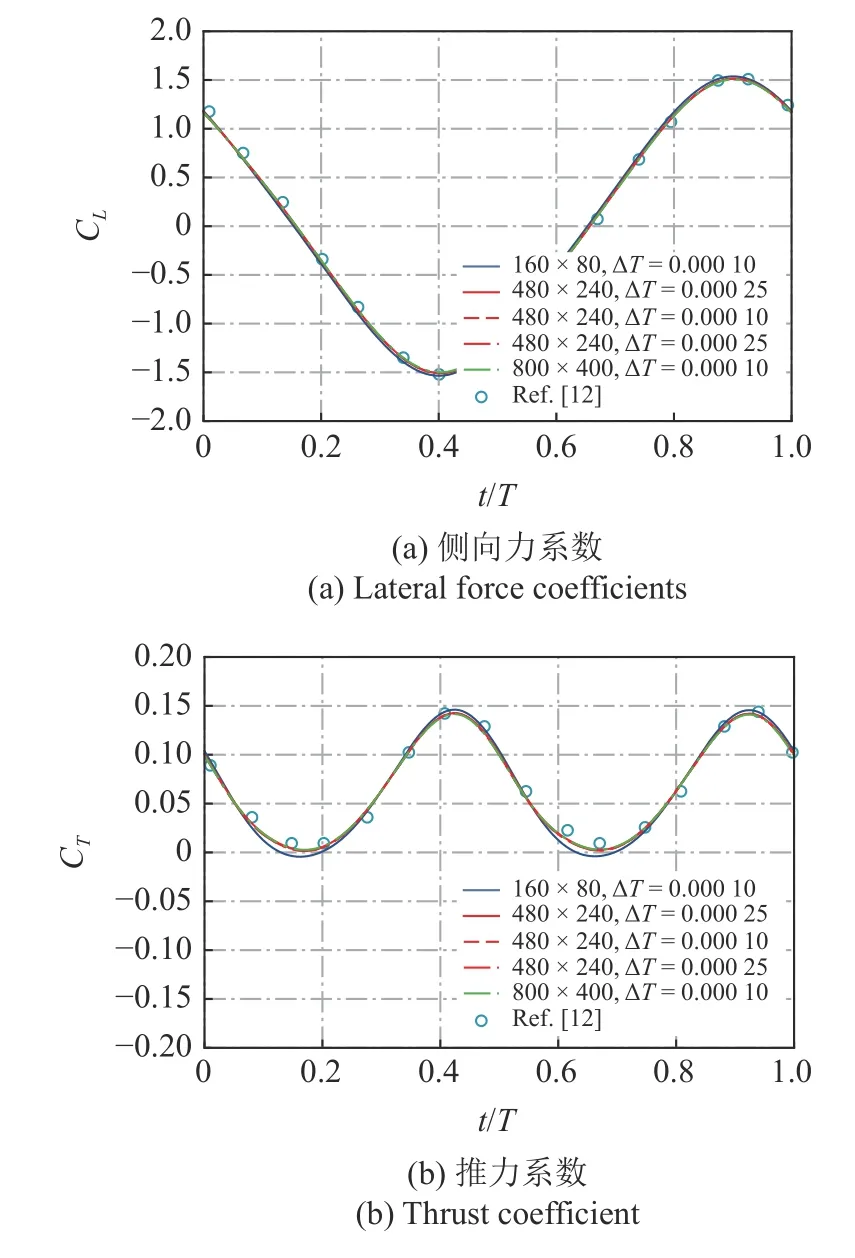
附图 A2 不同网格和时间步长的数值结果比较Fig.A2 Comparison of numerical results with different meshes and time steps

附录B 参考文献

B1 徐涛涛,胡文蓉.鳞鲀倒游机动的机理研究.水动力学研究与进展:A 辑,2022,37(3): 277-283 (Xu Taotao,Hu Wenrong.Study on mechanism of balistid’s backward maneuvering.Chinese Journal of Hydrodynamics,2022,37(3): 277-283 (in Chinese))