定常及振荡流下带网半浸没浮筒载荷特性研究1)

杨孟婕 任浩杰 胡滕艳 付世晓 张萌萌 许玉旺

(上海交通大学海洋工程国家重点实验室,上海 200240)

(上海交通大学海洋装备研究院,极地深海技术研究院,上海 200240)

引言

随着人们对海产品的需求增加,深远海养殖技术也随之发展[1-2].重力式网箱结构作为深海养殖的重要装备,研究其在复杂海洋环境下的服役安全性十分必要[3-7].重力式网箱系统主要组成部分包括浮圈、网衣、沉子和锚链[8].浮圈作为重力式网箱基本的顶部支撑结构,其在水平方向的阻力占网箱系统总阻力的28%[9],所以其水动力载荷计算对整体网箱结构的安全性设计十分关键[10].为更清楚地了解浮圈水动力载荷的作用机理,开展相关水动力特性实验十分必要.因此,开展以带网衣的浮圈为代表的半浸没圆形柱状浮筒水动力载荷特性研究具有重要的意义.

针对半浸没圆柱体浮筒水动力载荷问题,当前已有研究人员初步开展了一定研究,主要集中于探究半浸没浮筒水动力系数的变化规律和影响因素.Triantafyllou 等[11]研究了半浸没圆柱体的流动稳定性与Fr数之间的关系.研究发现基于势流理论,当Re＜ 25000 时圆柱下游位置均出现不稳定尾流.参考全浸没圆柱的两个重要影响参数—KC数(KC=UmT/D,其中Um为振荡最大速度,T为振荡周期,D为圆柱体直径) 以及Stokes 数[12](又称β数,β=Re/KC),Fu 等[13]研究振荡流及组合流下半浸没浮筒的水动力载荷以及KC数、β数、Re数对水动力系数的影响,结果表明自由表面对阻力系数影响较大,且会导致附加质量系数增大,振荡流下水动力系数与KC数和β数存在一定关系.胡克等[14]通过不同浸没深度的强迫振荡实验,发现自由液面上浪现象对于惯性力系数的影响较大.Ren 等[15]研究均匀流下不同浸没深度的部分浸没圆柱浮筒的水动力,实验表明由于自由表面的存在,阻力系数表现出与Fr数强相关关系,并初步拟合给出了半浸没浮筒的经验阻力公式.Ren 等[16]进一步考察振荡流场下阻力系数与附加质量系数分布规律,并考察了水动力系数对Fr数的依赖关系.研究发现与相同Stokes 数下的水动力系数与Fr数的关系相比,当相同KC数下,水动力系数随Fr数的增加有更明显演化趋势,使用Fr数和KC数来预测半潜式圆柱的水动力系数更为合理.Hu 等[17]研究定常及非定常流场下半浸没柱体水动力系数特征,结果表明,在定常流和振荡流的组合流场中,水动力系数与KC数几乎无关,而更可能受到Fr数的影响.以上对于半浸没柱体水动力的研究基本是对纯柱体展开,实验结果显示由于自由液面的存在会对半浸没柱体的阻力系数和附加质量系数存在较大影响,而且其水动力系数受Fr数的影响更大.但以上研究对象均为不带网衣的单纯半浸没柱体,并未考虑网衣对于半浸没浮筒的影响.

总体来看,目前对于网箱系统中带网衣浮筒水动力一般采用无网衣浮筒的水动力结果代替,并未考虑网箱系统中网衣对半浸没浮筒的影响,这与实际网箱系统的使用场景不相符,网衣对浮筒水动力载荷特性有何影响及影响程度需要进一步揭示.

为界定网箱网衣对半浸没浮筒水动力载荷特性的影响,本文开展带网衣的半浸没浮筒与无网衣半浸没浮筒的对比实验.实验中,将半浸没浮筒固定在拖车底部,以拖车带动浮筒运动来模拟定常流场;通过强迫运动机构强迫半浸没柱体以不同振幅和周期振荡,从而模拟半浸没浮筒受到的振荡流场.半浸没浮筒的两端布置三分力传感器,由编码器记录位移信息同步测量浮筒水动力载荷和强迫运动信息.进而由最小二乘法识别得出浮筒水动力系数,包括阻力系数和附加质量系数.对比研究了定常流和振荡流下带网衣的半浸没浮筒与无网衣浮筒载荷特性,并探究水动力载荷系数与敏感参数之间的关系.

1 半浸没浮筒水动力特性实验

1.1 实验装置

本实验在上海船舶运输科学研究所的拖曳水池中进行,拖曳水池长192 m,宽10 m,水深4.2 m,拖车最大速度为9 m/s.实验整体装置由强迫振荡装置、圆柱浮筒模型、假体和挡流板构成,如图1 所示.强迫振荡装置由两条垂直轨道和两条水平导轨构成.实验中,伺服电机驱动垂直轨道运动来调节实现浮筒的半浸没状态.伺服电机驱动水平轨道带动垂直轨道运动,继而强迫与垂直轨道相连接的浮筒在水中振荡.整个实验装置安装于拖车的下方,由拖车拖动固定于强迫振荡装置上的模型模拟定常流场.拖车静止不动时,通过强迫振荡装置强迫半浸没浮筒在静水中以不同幅值和不同周期振荡,模拟半浸没浮筒遭受的振荡流场,如图2 所示.

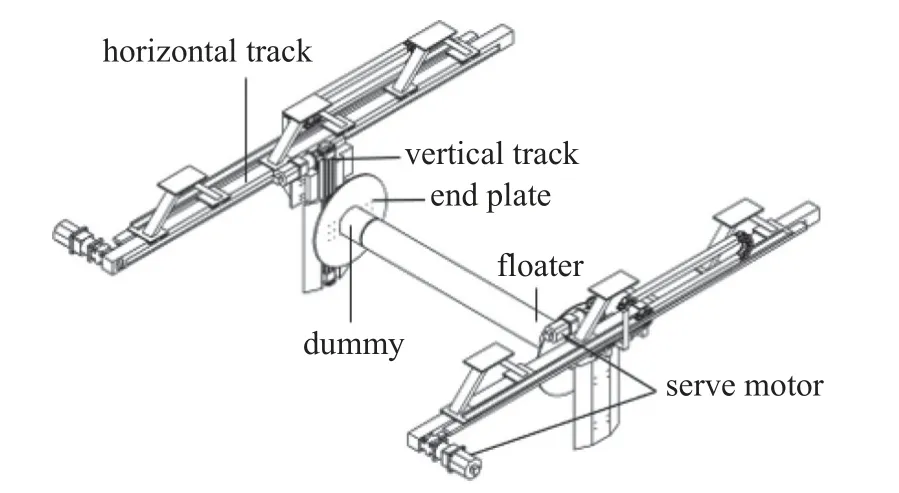
图1 实验装置示意图Fig.1 The sketch of oscillating experiment device

图2 强迫振荡实验图Fig.2 The photography of forced oscillation experiment

实验模型分为无网衣浮筒模型(SFM)以及带网衣浮筒模型(FNM),如图3 所示.SFM 为半浸没的光滑刚性圆柱体,由PP 材料加工而成,圆柱体长度L=2 m,直径D=0.25 m.FNM 为下部连接网衣的浮筒模型,网衣由尼龙材料编制而成,宽度为2 m,长度为3.5 m,网衣直径2 mm,半目长20 mm,密实度为0.4.根据实际重力式网箱形式,在网衣底部连接有一根钢制的沉子用于张紧网衣,沉子模型长2 m,直径0.0453 m,通过尼龙扎带与网衣连接.

图3 (a)无网衣浮筒模型和(b)带网衣浮筒模型Fig.3 (a) Single floater model and (b) floater-net model

实验中采用4 个三分力仪测量模型的受力,浮筒两侧装有2 个三分力仪用于测量SFM 或FNM 整体的受力;网衣上部连接在挂杆上,挂杆两端连接另外2 个三分力仪,布置于浮筒内部,用于测量FNM中网衣的受力,如图4 所示.为保证流经圆柱浮筒模型的流动二维性,在浮筒模型两端安装与浮筒模型直径相同的两段假体,并在两段假体外侧安装有两个圆形挡流板用于减少边界条件的影响.假体和模型之间留出一小块空间(＜ 1 mm),以保证力传感器仅测量模型上的力.

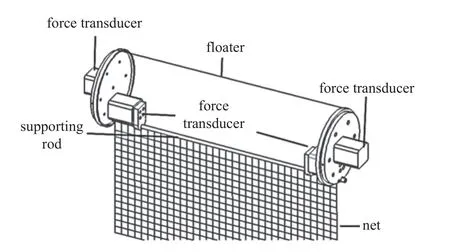
图4 三分力仪布置图Fig.4 The arrangement of the three-dimensional force transducers

1.2 实验工况

为了揭示网衣对半浸没浮筒水动力特性的影响,本实验制定SFM 和FNM 所遭受的典型流场工况,包括定常流场工况和波浪次生振荡流场工况,如图5 所示.定常流工况流速选择主要覆盖实际海况的表面流速范围,振荡流工况选取实际海况中养殖网箱所遭遇的几种典型周期和幅值[13].通过对比两种工况下带网衣与不带网衣的半浸没浮筒水动力特性,说明网衣对半浸没浮筒水动力的影响.x轴沿拖车拖曳方向,y轴垂直于拖车模拟的定常流方向.刚性圆柱体浸没深度h=0.5D.

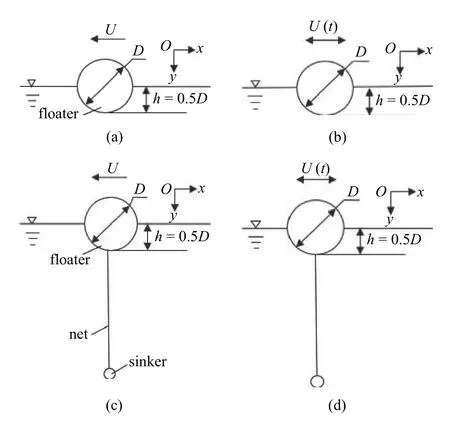
图5 实验工况示意图Fig.5 Sketch of the experimental cases

表1 所示为具体设置的实验工况.实验制定定常流和振荡流两种工况,每种工况分别进行SFM 和FNM 两种模型的实验.定常流工况流速为0.2,0.4,0.8 和1.2 m/s,对应Re数范围为5.0×104～3.0 ×105,Fr数范围为0.18～1.08.振荡流工况振荡幅值设置为0.25,0.75 和1.25 m,振荡周期设置为5.5,8.5 和11.5 s,对应Re数范围为3.4×104～3.6×105,对应Fr数范围为0.12～1.29.

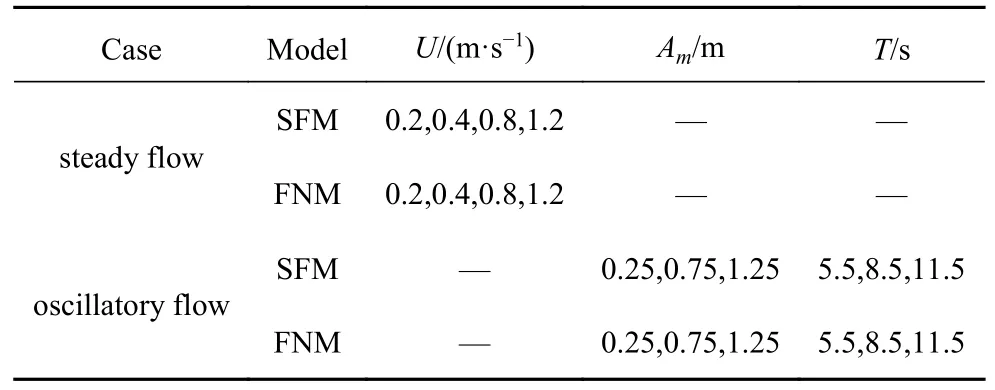
表1 实验工况表Table 1 Details of the test cases

1.3 圆柱水动力主要影响参数

本实验设置两种流场工况,针对定常流场而言,半浸没圆柱体水动力的关键影响参数主要有Re数和Fr数[11,18-19].振荡流场下,半浸没圆柱体水动力的影响参数不仅包括Re数和Fr数,还受KC数和Stokes 数(β数)的影响[20].为了区分定常流场和振荡流场的参数,将定常流下Re数定义为定常雷诺数(Re),振荡流场下Re数定义为最大雷诺数(Re*);同样,定常Fr数(Fr) 对应定常流场,振荡Fr数(Fr*)对应振荡流场.以上参数定义如下

式中,U0为定常流速度;Um为振荡最大速度;D为浮筒直径;ν为水的运动学黏性系数,ν=1.0 ×10-6m2/s;h为浸没深度,h=0.5D;Am为振荡最大振幅;T为振荡周期.

2 基本理论

2.1 莫里森方程

对于网箱浮圈这类小尺度柔性构件,工程上通常采用莫里森方程[21]进行水动力计算.由于实际使用莫里森公式时很难确定半浸没浮筒的瞬时湿表面积,为了方便工程应用,均采用浮筒直径作为水动力直径[15,22].

(1)定常流

定常流场下半浸没圆柱体的平均阻力可以写成[23]

式中,FD为平均阻力;为平均阻力系数;D为刚性圆柱体的直径;L为刚性圆柱体的长度;U为定常流流速;ρ为流体密度,ρ=1000 kg/m3.

(2)振荡流

对于本实验在静水中强迫振荡的半浸没圆柱体载荷可以由莫里森方程表示为

式中,F为总载荷;CD为阻力系数;CA为附加质量系数;U(t)和(t)分别为流体相对于圆柱体的相对速度和加速度.

2.2 水动力系数识别

(1)定常流下

定常流下半浸没浮筒的阻力系数由式(1)可得

(2)振荡流下

利用最小二乘法将水动力系数从强迫振荡实验测得的水动力时间序列中提取出来.由最小二乘法得振荡流下圆柱体受力的误差平方和可以表示为

式中,F(ti)为测量得到的半浸没圆柱水动力实际值;Fm(ti)为基于莫里森公式求解得到的半浸没圆柱的水动力理论值.

由式(2)得半浸没圆柱水动力得理论值为

将式(5)代入误差平方和式(4)可得

进一步定义

之后式(6)可以简化为

为使误差平方和取到最小值,应满足以下两个条件

求解方程组(8),最终可以得到阻力系数CD和附加质量系数CA

3 结果及讨论

为揭示网衣对半浸没浮筒水动力影响,首先对纯浮筒模型与带网浮筒模型的水动力载荷特性进行对比研究,为后续水动力系数的探究提供一定基础.进而根据以上的数据处理方法得到定常流及振荡流下半浸没浮筒的水动力系数,并对水动力系数与Re数、KC数和Fr数等关键参数之间的关系进行了进一步探究.为了简化描述,以下正文及图片中纯浮筒均代指无网衣浮筒模型中的浮筒(SF);带网浮筒均代指带网衣浮筒模型中的浮筒(NF).

3.1 带网浮筒水动力载荷特性

(1)定常流

图6 给出定常流不同流速工况下带网浮筒与纯浮筒水动力时历图.由图6(a)～图6(c)中可以看出,流速为0.4,0.8 和1.2 m/s 工况下,纯浮筒的平均阻力大约分别为12 N,28 N 和106 N,而带网浮筒的平均阻力大约分别为36 N,113 N 和214 N.两者对比,流速为0.4,0.8 和1.2 m/s 工况下,带网浮筒的阻力相对纯浮筒,分别放大了3 倍、4 倍和2 倍.以上结果可以看出,网衣的存在急剧放大了浮筒所遭受的水动力载荷,这表明网衣对浮筒载荷影响无法忽略.目前带网浮筒模型在定常流作用下通常认为网衣为主要受力结构,浮筒受力可以忽略[24].根据本工作发现的网衣对浮筒水动力的放大效应,说明传统采用纯浮筒所测水动力载荷结果会导致结构设计偏于危险.因此,网箱结构设计中对浮筒水动力的计算应当考虑网衣影响.

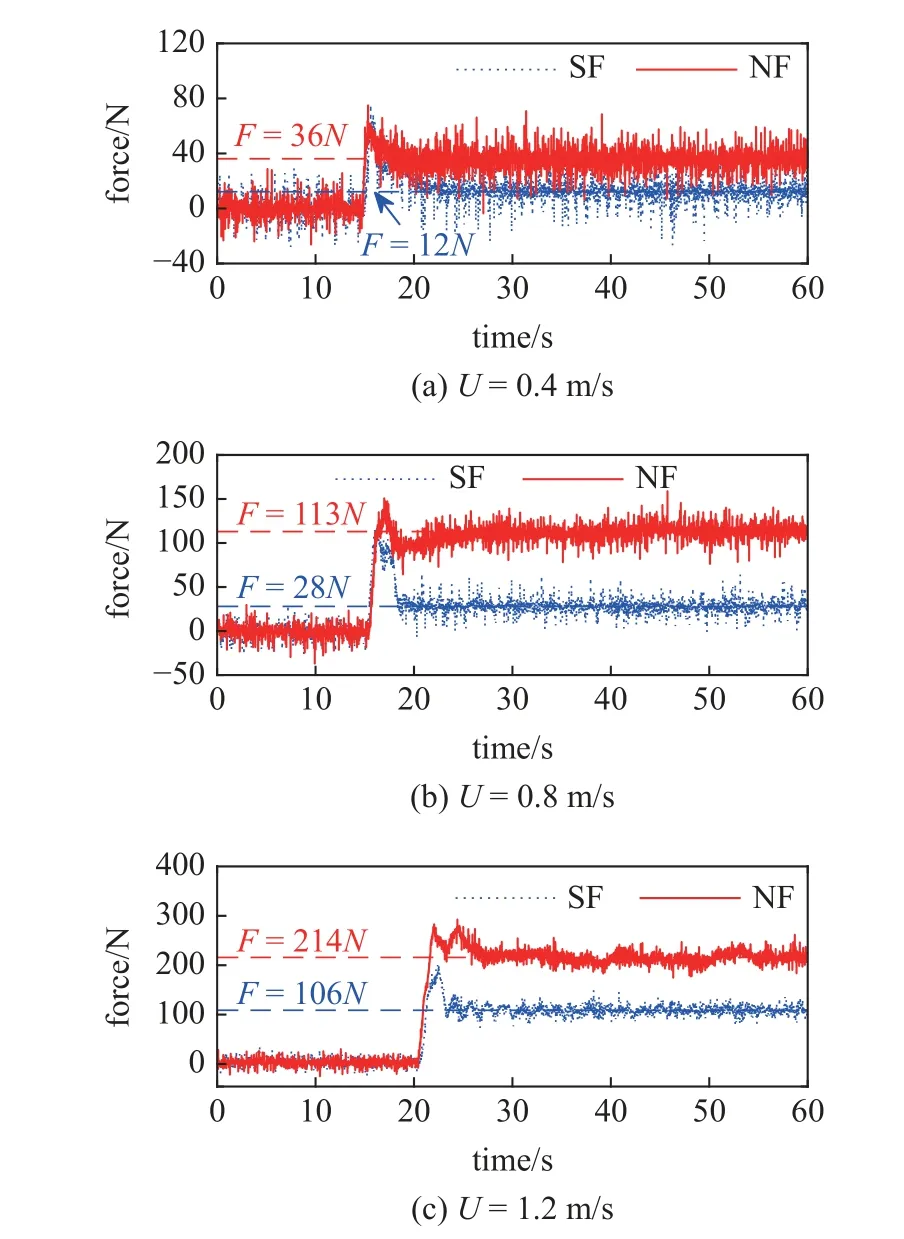
图6 定常流下水动力实验结果时历图Fig.6 Time history of the hydrodynamic forces under steady flow

进一步地,本工作汇总不同流速工况下纯浮筒与带网浮筒的阻力均值,如图7 所示.图7 中结果显示: 在低流速下,网衣对浮筒阻力放大效应更为显著,当流速增大,即Re数上升后,这种阻力放大效应有所减弱.当Re数5.0×104增长至3.0×105,带网情况下浮筒阻力放大比例从680% 减弱为102%.

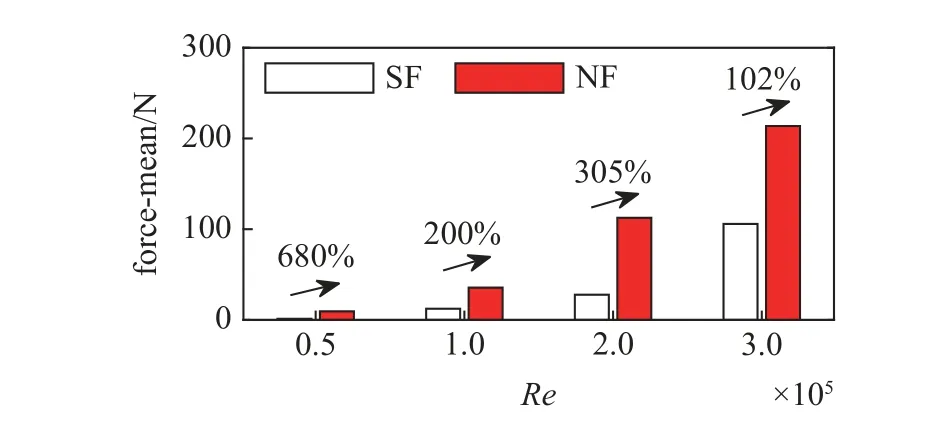
图7 定常流下水动力均值对比直方图Fig.7 Bar graph of the mean hydrodynamic forces under steady flow

出现以上现象的原因可能是由于随着流速的增加,带网浮筒模型中网衣的变形逐渐加大,网衣与自由液面之间夹角在缩小,也就是网衣逐渐趋向平行于自由液面,此时对流场的阻滞作用也逐渐减小,因此随Re数增加,网衣对半浸没浮筒的影响逐渐减小.而随着Re数的增加,这种放大比例不是呈现出单调的减小现象,其中可能的原因是半浸没柱体以及网衣阻力随着Re数并不是同步性变化的,网衣的倾斜角度变化也不会随着Re数呈固定比例的增大,因此导致网衣对半浸没柱体的载荷放大效应不会呈现出单调性的减小.

(2)振荡流

前述,本工作发现定常流下网衣结构会急剧放大浮筒所遭受的阻力载荷.而波浪环境下带网浮筒总受力中浮筒受力的占比要高于单纯定常流中浮筒受力的占比[25].因此,波浪次生振荡流下,网衣对浮筒水动力载荷的影响亟待考察.

为了考察不同振荡程度的振荡流场中带网浮筒的水动力特性,本文选取同一振幅Am=1.25 m 时,不同周期的振荡流作用下纯浮筒与带网浮筒的载荷时历图,如图8 所示.图8 中可以看出周期分别为5.5,8.5 和11.5 s 时,纯浮筒的载荷最大值()分别为240 N,75 N 和47 N,带网浮筒的载荷最大值分别为400 N,149 N 和100 N.对比两条曲线,可以看出带网浮筒的载荷值分别是单纯浮筒的1.66 倍、1.98 倍和2.11 倍.这与定常流下网衣对半浸没浮筒的放大效应是一致的.

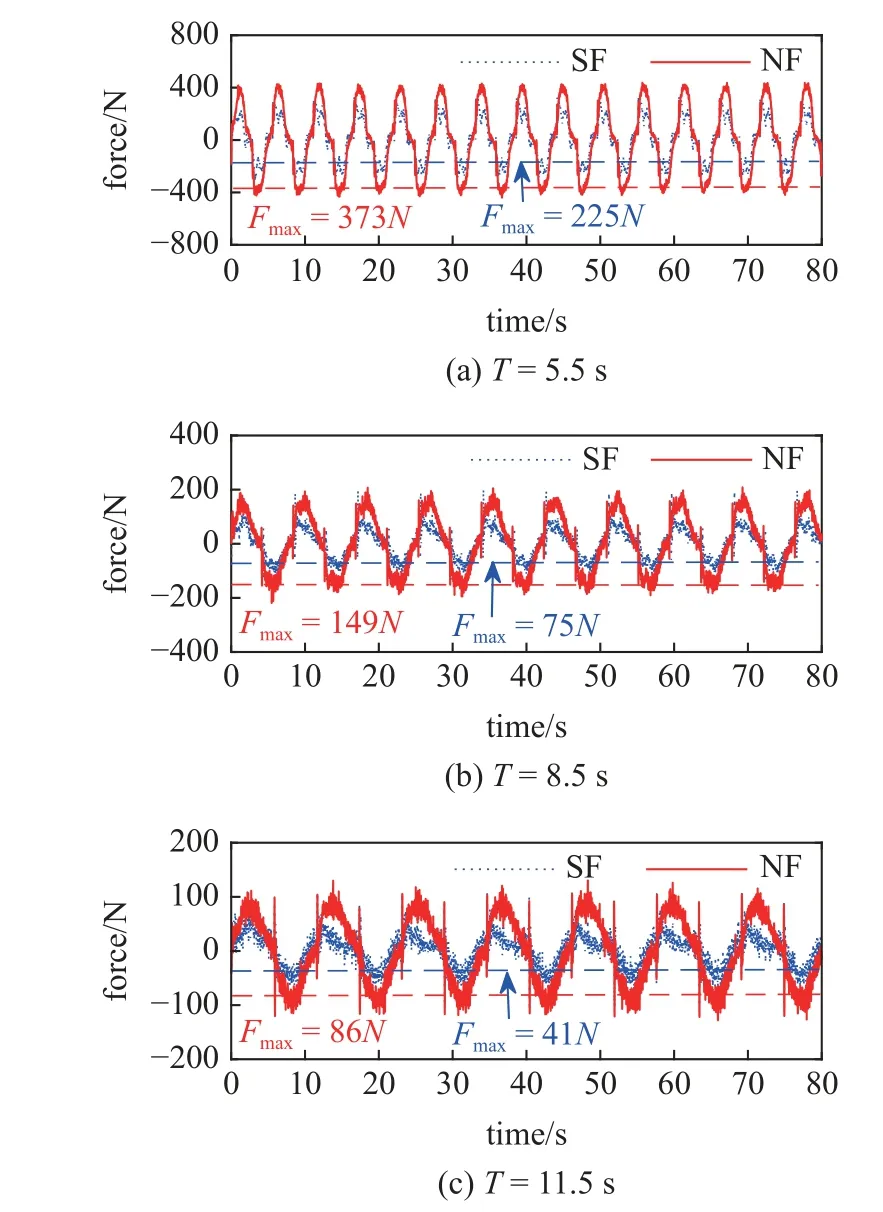
图8 振荡流下水动力实验结果时历图Fig.8 Time history of the hydrodynamic forces under oscillatory flow

为了进一步展示这种放大效应,图9 中汇总了所有振荡流工况下纯浮筒与带网浮筒载荷的RMS值对比直方图.图9 中可以明显的看出在同一振幅,不同周期下,几乎带网浮筒的阻力与单纯浮筒相比都有一定程度的增大,且随周期增大,阻力值的增长幅度也在增大.同一振幅下周期增大,速度最大值减小,网衣变形也对应减小,这与均匀流时水动力放大效应比较类似.

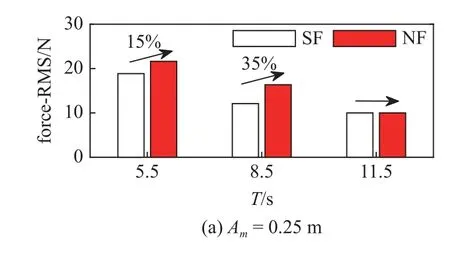
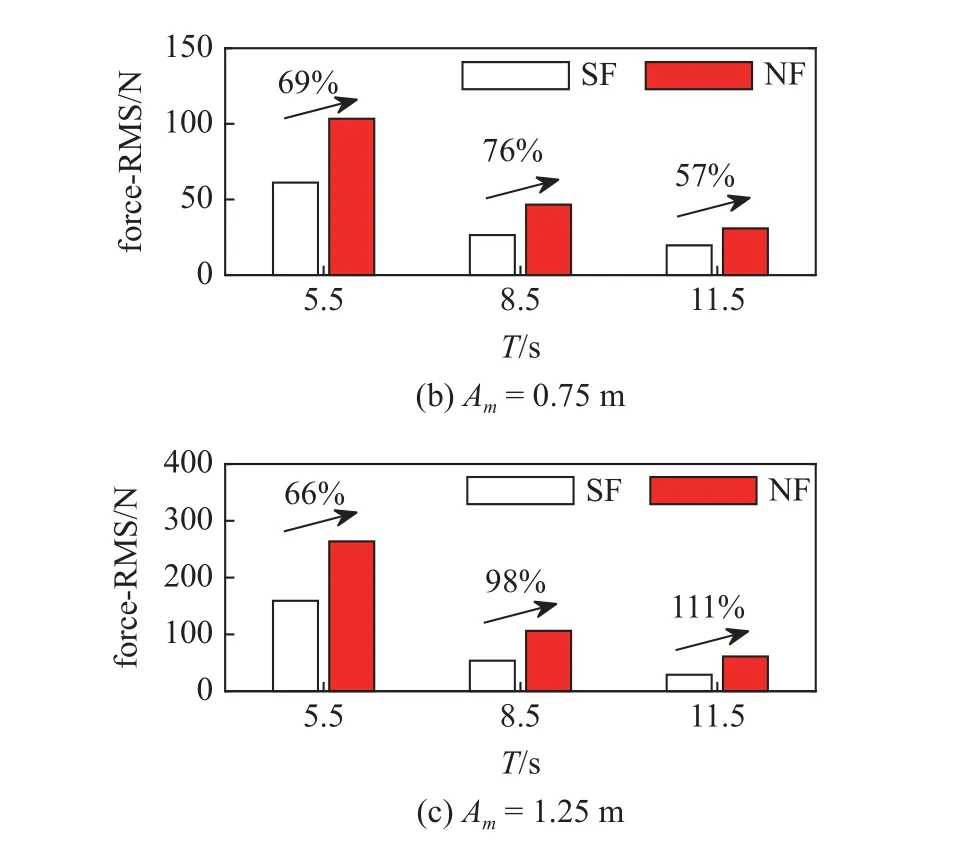
图9 振荡流下水动力RMS 值对比直方图Fig.9 Bar graph of the RMS hydrodynamic forces under oscillatory flow

由以上实验结果可以看出在定常流以及振荡流环境下,由于网衣存在,带网浮筒的水动力较纯浮筒相比被放大,且放大效应随Re数增加有所下降,因此网衣对于半浸没浮筒水动力的影响不可忽略,这在网箱设计以及整个服役中时需要重点关注的问题.

3.2 带网半浸没浮筒阻力系数

通过带网浮筒水动力载荷的研究,发现网衣对半浸没浮筒水动力有显著的放大效应,为进一步探究带网半浸没浮筒水动力系数的影响因素,利用最小二乘法等数据处理方法进行水动力系数的识别,研究了Re数、Fr数、KC数以及Stokes 数对带网衣浮筒水动力系数影响.

(1)定常流下

图10 所示的为定常流下单纯浮筒与带网浮筒模型的阻力系数与Re数的关系,从图10 中可以看出在Re数5.0×104～3.0×105范围内,带网浮筒与单纯浮筒的阻力系数相比均有显著增加.对比两条曲线,可以看出带网浮筒的阻力系数大约为纯浮筒的2.65 倍.网衣对于半浸没浮筒的阻力系数也表现出放大效应.

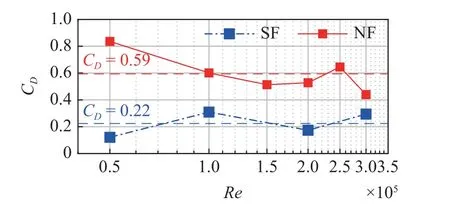
图10 定常流下模型的阻力系数与Re 数的关系图Fig.10 Relationship between drag coefficient and Reynolds number under steady flow

为了研究现象产生的原因,在设备上安装了摄像头记录实验现象.在圆柱体的上游和下游可以清晰地观察到局部表面变形,如图11 所示.对于均匀流下单纯浮筒模型可以看到自由液面的爬升和下降分别出现在圆柱的上游和下游,这表明在这种情况下会出现不对称涡流脱落和倾斜压力分布[15],此时上下游压力差较小;对于带网浮筒模型可以看到上游出现自由液面的爬升,下游由于网衣的存在,其水面下尾涡形成受到抑制,导致流场比较紊乱,并未出现明显的自由表面下降,因此与单纯浮筒相比,圆柱上游和下游的压力差增大,阻力也随之增大.

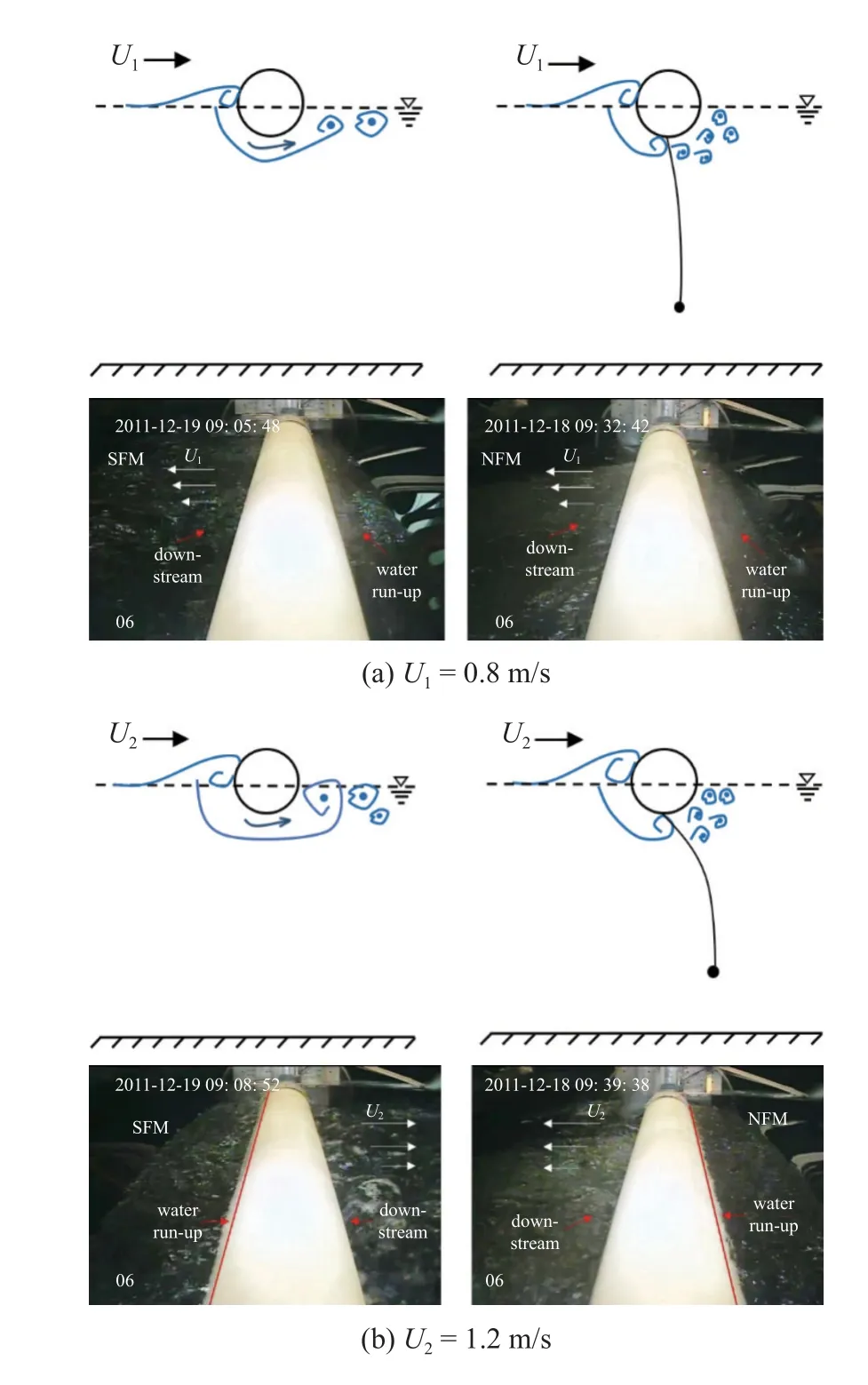
图11 流速为0.8 m/s 和1.2 m/s 时半浸没浮筒涡街示意图与实验照片Fig.11 Picture and sketch of the vortex streets under a flow velocity of 0.8 m/s and 1.2 m/s

随着Re数的增大,带网浮筒与单纯浮筒的阻力系数差距减小.Re数为5.0×104时,带网浮筒阻力系数几乎为单纯浮筒的5 倍,Re数增大为3.0×105时,网衣对浮筒阻力系数的放大效应下降为1.5 倍,这与3.1 节中阻力放大效应减弱相对应.对比图11(a)和图11(b)中不同流速的实验结果可以看出,随着流速的增加,网衣的变形增加,带网浮筒后方尾流紊乱程度增加,因此流场紊乱的分离点随网衣变形而逐渐后移,所以随Re数增加,带网浮筒与单纯浮筒阻力的差值在减小.

Ren 等[15-16]提出均匀流下半浸没浮筒阻力系数与Fr数呈强相关关系,因此本工作也对应做了相关探究.图12 为定常流下阻力系数与Fr数之间的关系图.从图12 中可以看出对于纯浮筒,阻力系数基本维持在0.22 左右;对于带网浮筒,Fr数在0.18～0.90 范围内,阻力系数与Fr数存在二次相关关系,这也说明由于自由表面的存在,破坏了泄涡的对称性,随着Fr数的增加,自由表面的变形也加大[25].

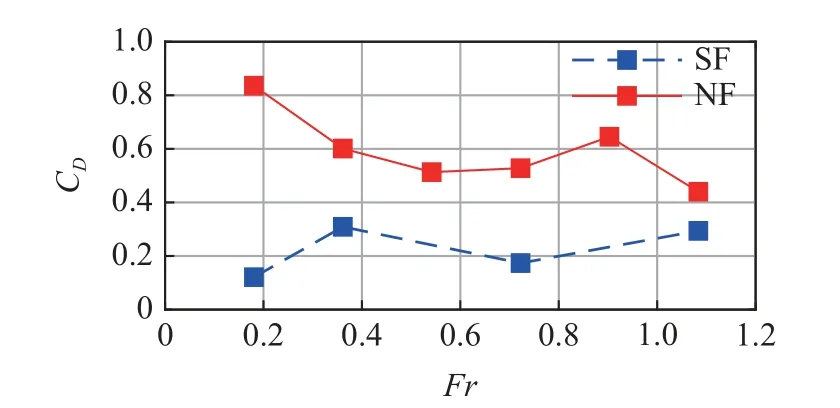
图12 定常流下模型的阻力系数与Fr 数的关系图Fig.12 Relationship between drag coefficient and Fr number under steady flow

(2)振荡流

振荡流下模型的阻力系数可以通过式(9)得出,图13 给出不同β数的振荡流作用下阻力系数与KC数的关系.图中可以明显看出网衣对浮筒的放大效应同样存在.同一β数下,随KC数的增加,纯浮筒阻力系数变化幅度较小,但带网浮筒的阻力系数呈明显的下降趋势,且网衣对阻力系数的放大效应也明显减弱.如图14 所示,半浸没浮筒在振荡过程中由于液面爬升浸没体积不断变化,随着浸没体积的增加阻力系数不断减小[26].随着KC数的增加逐渐出现上浪和兴波现象,但带网浮筒由于网衣的存在,兴波现象程度明显小于单纯浮筒,此时因为兴波造成的能量输入较小,因此阻力系数的差距逐渐缩小.

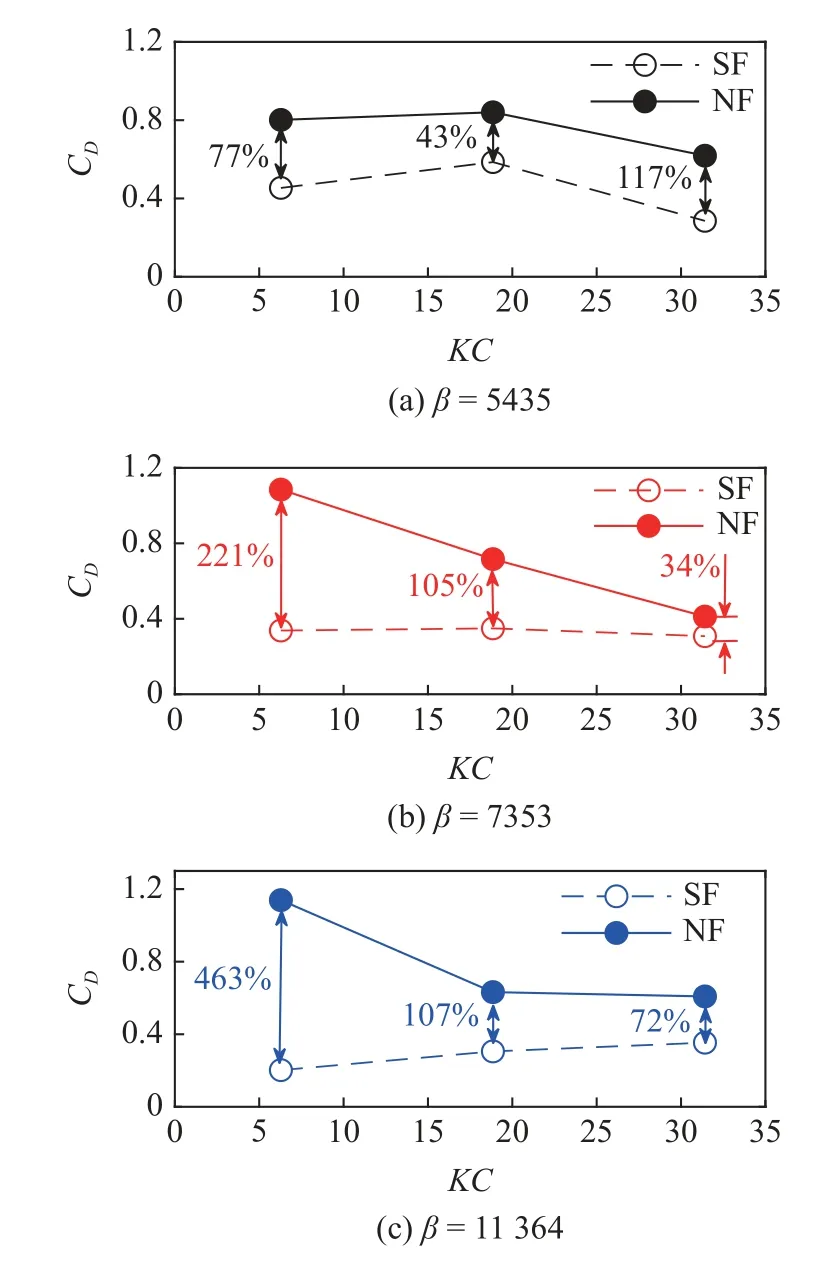
图13 不同β 数的振荡流作用下阻力系数与KC 数的关系图Fig.13 Drag coefficient versus KC number under different β number

图14 大KC 数下的实验图Fig.14 Picture at high KC number

图15 所示为不同KC数下带网浮筒与单纯浮筒的阻力系数随Fr数的变化图.从整体分布来看,(1)单纯浮筒阻力系数随着Fr数的增加,总体呈现下降趋势,且与Fr数存在一定的演化关系;(2)带网浮筒阻力系数在低Fr数和高Fr数下分布规律呈现一定的差异性,在Fr＜ 0.3 时,带网浮筒的阻力系数呈现上升趋势,在Fr＞ 0.3 时,带网浮筒的阻力系数整体呈现下降趋势;(3) 带网浮筒的阻力系数与Fr数保持一定的演化趋势,随着Fr数增大,网衣对浮筒阻力系数的放大作用减弱.综上可以看出,单纯浮筒和带网浮筒的阻力系数与Fr数具有一定的相关性.

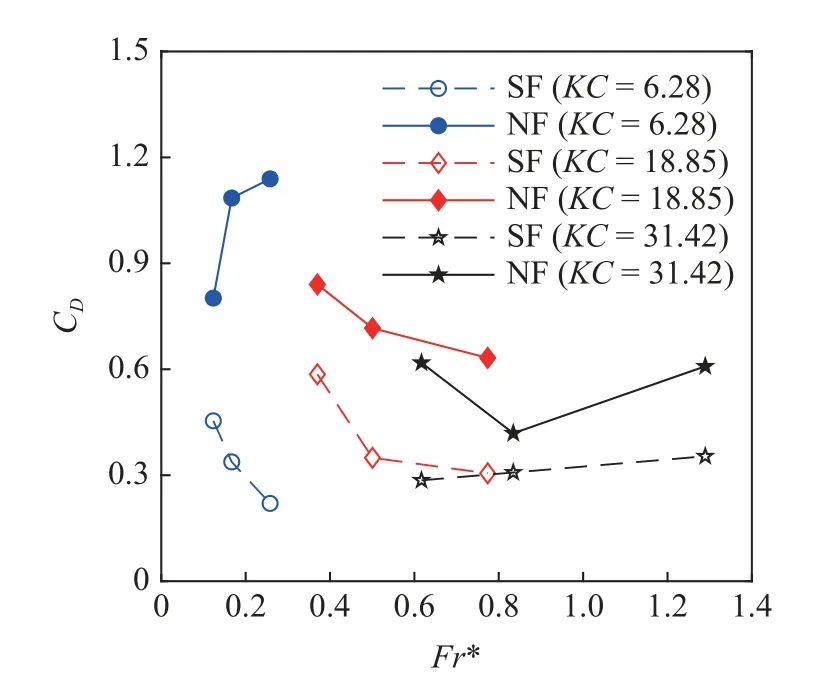
图15 不同KC 数下Fr 数与阻力系数的关系图Fig.15 Drag coefficient versus Fr number under different KC number

3.3 带网衣半浸没浮筒附加质量系数

振荡流下模型的附加质量系数可以通过式(9)得出,不同β数的振荡流下单纯浮筒与带网浮筒模型的附加质量系数与Fr数的关系如图16 所示,可以看出相同β数下,模型的附加质量系数与KC数基本成线性增加的关系.对比两者曲线发现带网浮筒的附加质量系数整体大于单纯浮筒的附加质量系数,且基本随KC数增加,网衣对附加质量的放大效应不断增大.

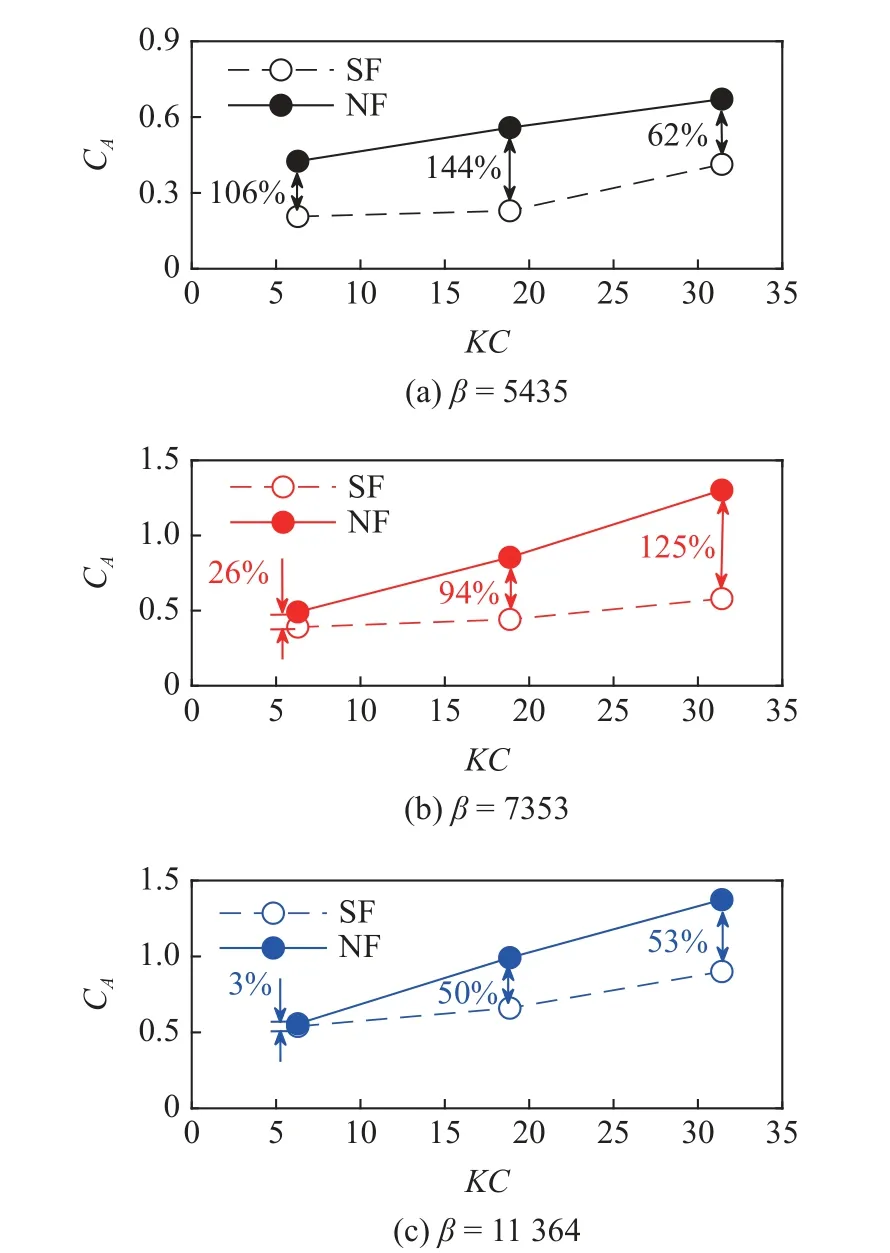
图16 不同β 数的振荡流作用下附加质量系数与KC 数的关系图Fig.16 Added mass coefficient versus KC number under different β number

自由液面的存在[24,27-30]会对半浸没浮筒的附加质量系数产生一定的影响.结合实验录像,半浸没圆柱浮筒在振荡过程中大于其静止状态的湿表面积,拖曳速度的增大,使得圆柱的排水体积增大,使得其附近的压力梯度也在增大.随着KC数增大,半浸没圆柱表面出现明显的上浪和兴波现象,且单纯浮筒与带网浮筒相比,圆柱下游出现明显的波浪破碎,卷入大量气体,导致下游表面水体不易附着,因此附加质量系数的差距进一步增大,如图17 所示.

图17 小KC 数下水体附着示意图Fig.17 Sketch of attached water at low KC number

图18 所示为不同KC数下Fr数与附加质量系数的关系图,图18 中附加质量系数与KC数的区域性分布以及附加质量系数与Fr数的相关关系更加明显.纯浮筒以及带网浮筒的附加质量系数均表现出随Fr数增加而增加的趋势,且随着Fr数的增加,带网浮筒附加质量系数的与纯浮筒的差距明显增大.进一步说明与KC数相比,Fr数与半浸没浮筒附加质量的相关性更强.

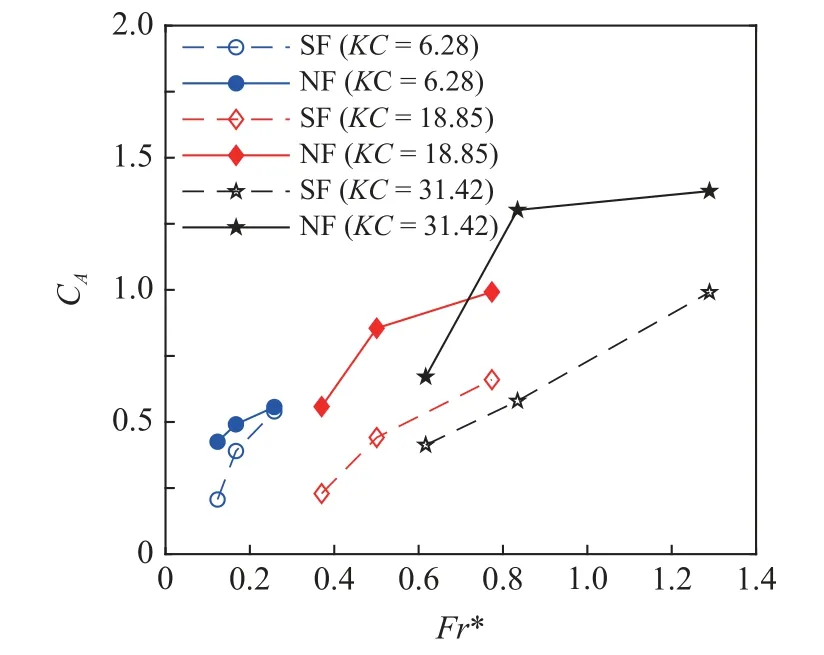
图18 不同KC 数下Fr 数与附加质量系数的关系图Fig.18 Added mass coefficient versus Fr number under different KC number

4 结论

通过带网半浸没浮筒模型和单纯半浸没浮筒在拖曳水池中进行拖曳以及利用强迫振荡装置模拟定常流以及振荡流环境条件,利用最小二乘法等对数据处理得到各工况的水动力系数,对比两种模型的实验结果,得到以下主要结论.

(1)定常流及振荡流下,带网半浸没浮筒水动力与单纯浮筒相比成倍数增加,网衣对半浸没浮筒水动力具有明显的放大效应.因此网衣的存在对半浸没浮筒水动力的影响不可忽略.

(2)定常及振荡流下,带网半浸没浮筒的阻力系数远大于单独浮筒.在振荡流场中,对比不同敏感参数,结果单纯浮筒和带网浮筒的阻力系数均与Fr数保持一定的演化趋势.随着Fr数增大,网衣对浮筒阻力系数的放大作用减弱.

(3)振荡流下,网衣对半浸没浮筒的附加质量系数同样呈现出明显的放大效应.通过对比KC数与Fr数对附加质量系数的影响,发现附加质量系数同样对Fr数的变化更加敏感.网衣放大效应随Fr数的增加而增大.

本工作对带网半浸没浮筒的水动力计算十分重要,对实际工程中重力式网箱的浮圈设计起到有益帮助.