考虑气核生长溃灭效应的螺旋桨梢涡空化初生数值模拟研究1)

王永帅 王鑫程 程怀玉 季斌

(武汉大学水资源工程与调度全国重点实验室,武汉 430072)

引言

空化是指液体压力下降到蒸汽压以下,液体转变为蒸汽的相变过程,在各种水轮机、泵和船舶推进器等水动力设备中尤为常见[1-2].在螺旋桨中,空化的发生可能导致噪音、振动和性能下降等一系列问题[3-6],严重影响海军舰艇的声隐身性.因此世界各国海军引入并发展了一种评价螺旋桨空化性能的指标—临界航速.在实船螺旋桨上,梢涡空化往往是最早发生的空化类型,因此梢涡空化初生是舰船临界航速判断的重要依据.梢涡空化不能仅仅以恒定的饱和蒸汽压作为临界条件,水中气核富集对于梢涡空化的发生也有着举足轻重的影响[7].因此对螺旋桨梢涡空化初生进行精准的数值预报与空化初生时气核运动生长溃灭效应密切相关,且对于军舰临界航速的精准预报具有十分重要的意义.

在实验中,螺旋桨梢涡空化初生的预报往往是通过观察螺旋桨叶片尾流中有无细小空穴的出现[8-9].但实际上在观测到细小空穴前往往就已经出现难以观测到的微观气核暴发式生长与快速溃灭收缩的过程,并产生强烈的脉冲声压[10].受限于实验测量仪器的精度和环境背景噪声污染,这种脉冲声信号往往也难以测量.因此,螺旋桨空化初生的实验预报方法不仅成本高而且往往会在一定程度上低估空化的发生.

近些年随着高性能计算机的快速发展,越来越多的研究借助计算水动力学来研究螺旋桨中的空化流动[11-17].但是传统欧拉框架下的宏观空化模型不仅无法直接考虑微观气核的影响并且严重依赖于梢涡处的局部网格分辨率[18].因此有必要发展一种新的梢涡空化初生数值预报方法来对螺旋桨梢涡空化初生进行精准预报与研究.

近年来,基于气泡动力学理论的拉格朗日框架与欧拉框架相结合的空化初生数值预报方法发展迅速.1917 年,Rayleigh[19]首先分析了自由场中的气泡动力学,提出忽略可压缩性、表面张力和黏度的常微分方程来描述气泡的演化过程.在Rayleigh 方程的基础上,Plesset[20]发展了一个考虑表面张力和黏度的新方程Rayleigh-Plesset (R-P)方程,极大地推动了气泡动力学的研究进程.随后,Trilling[21]在R-P方程基础上修正得到的Herring-Trilling 方程考虑了流体压缩所储存的能量,并在考虑声场辐射和液体可压缩性后给出关于膨胀率较低的气泡坍塌的更好描述,但多适用于气泡在不受干扰的液体中溃灭过程并且对于不可凝结气体影响的考虑并不够充分.Gilmore[22]基于Kirkwood-Bethe 假设进一步提出考虑可压缩性的气泡动力学方程.虽然通过该理论模型可以找到球形气泡的运动规律,但是该模型适用于驱动压力较高的工况,并且在复杂流场中很难直接得到解析解[23].因此,现有诸多关于水力机械中复杂空化流动的研究大多基于R-P 方程或在其基础上简化改进形式的气泡壁面运动模型展开.

Hsiao 等[24-27]对该理论进行了完善,提出SAP球形气泡模型,并应用到螺旋桨空化初生的预报中.该模型用气泡表面平均压力代替气泡中心点处压力,并且考虑了气泡与流体之间的滑移速度影响,在计算过程中得到相对满意的结果.熊鹰等[28]同样用该模型研究了螺旋桨梢涡空化的初生问题,计算得到的螺旋桨梢涡空化初生空化数高于试验观察值.但是,他们对螺旋桨梢涡空化初生的研究多采用雷诺时均方法计算欧拉流场而无法求解涡心的脉动成分,且未结合具体涡流场深入研究空化初生过程中气核的运动生长溃灭过程.此外,现有模型大多没有重点强调气泡溃灭过程中由于其表面向内收缩的速度较大且过程极短而不容忽视的液体的可压缩效应.

随着研究的深入,气泡动力学理论进一步得到完善.Zhang 等[29]不仅建立空化气泡、水下爆炸气泡和气泡振荡等气泡动力学的新理论,还首次提出实用性强且能够同时考虑边界、气泡相互作用、流体可压缩性和表面张力等诸多因素影响的气泡动力学方程.并在其另一项研究成果中详细阐明考虑压力波传播过程的中心气泡与周围气泡群之间的相互作用[30].这进一步说明在空化过程中考虑气核影响和液相可压缩效应的重要性.

因此,为了弥补传统空化模型以及现有基于气泡动力学模型对于梢涡空化初生预报的不足,本文发展并采用能够同时考虑气核运动、生长溃灭、不可凝结气体和水相可压缩效应的梢涡空化初生的数值预报模型,并结合应力混合涡模型(SBES)对螺旋桨梢涡初生空化进行准确的数值预报,研究不同来流气核尺寸对螺旋桨梢涡空化初生的影响以及梢涡流动特性对气核演变的影响机制,并进一步探究单个气核在梢涡流场中的发声机理,以期为舰船临界航速和初生空化噪声的精准数值预报提供参考依据.

1 连续相模拟

1.1 控制方程

控制方程为雷诺平均N-S 方程,且假设流体不可压缩.三维流动的质量守恒方程和动量守恒方程为

式中,ρ是流体密度,fi是体积力,ui和代表i方向的速度,μt和μ分别是湍流黏度和动力黏度.

1.2 湍流模型

相较于传统的雷诺平均湍流模型(RANS),以大涡模拟(LES)求解大尺度湍流结构的主流区域,而以RANS 方程求解以黏性耗散为主的近壁面边界层的混合模拟方法对复杂湍流流动的捕捉能力更强,更适用于螺旋桨梢涡流动细节的捕捉[31-32].但传统的RANS/LES 混合方法如分离涡模型(DES)和延迟分离涡模(DDES)在计算过程中容易出现模化应力不足和过度保护的问题[33].而SBES 模型则不具有上述缺点且没有明显的网格依赖性[34-35].SBES 模型是通过使用屏蔽函数fSBES实现RANS 到LES 区域的快速自动切换[36].通过该屏蔽函数可用于实现RANS 和LES 在应力水平上的混合

当两个模型都基于涡黏假设时,式(3)可简化为

在本文中,当fSBES=1 时采用曲率矫正的SSTk-ɷ模型[37]求解边界层区域,而当fSBES=0 切换LES WALE 模型[38]处理远离壁面的大尺度湍流区域.

2 离散相单泡模型

初生涡空化的演变主要受到气核、涡心低压以及低压作用时间3 个因素的耦合影响[39].在梢涡初生空化流动中,气核在涡流场压力梯度作用下会向涡心富集,到达低压而发生暴发式生长,并在压力回升时迅速溃灭.因此,气核的受力运动状态以及生长溃灭行为就需要被充分考虑.而传统的均相流模型无法求解气核被卷入涡心的过程、极微小时间尺度和空间尺度下的流动特征以及气核的生长和溃灭对远场噪声的重要影响,从而会低估初生空化流动及其噪声.本文中采用离散的球形气泡模型来描述梢涡流动中气核的受力运动状态和生长溃灭行为,它们分别由气泡迁移方程和气泡脉动方程所描述.

2.1 气泡迁移方程

气核的运动轨迹是由牛顿第二定律决定

式中,x,ub和mb分别代表着气泡的位置、速度和质量.F则是由施加在气泡上的各种力所组成.气核在梢涡流中运动的准确位置对目前研究十分重要,其中确定施加在气泡上的力是关键.气核的受力主要包含阻力、升力、浮力、附加质量力、压力梯度力以及体积变化力,其中对于初生涡空化问题,阻力FD、压力梯度力FPG、体积变化力FV和附加质量力是影响气核在流场中运动轨迹的主要因素[40-42],因此本文仅考虑这4 种力对气核的作用,则式(6)表达为

式中,右边3 项分别代表阻力、压力梯度力以及体积变化力.Rb为气核半径,ρl为欧拉场密度,p为欧拉场压力.CD为阻力系数,可由下面的经验公式表达

其中,Reb为气核雷诺数

2.2 气泡脉动方程

泡在径向的变化主要由Rayleigh-Plesset (R-P)方程来反映.应该指出的是,本文讨论的流动条件总是具有较高空化数的空化初生工况,因此气核的暴发式生长不会持续很久,这大大抑制了气泡沿梢涡轴线的变形[43].所以,在本研究中采用球形气泡的假设是可行的.考虑到运动的气核与当地流体之间存在速度差,并会由此造成一个作用在气核表面的附加压力项,其大小为(u-ub)2/4.则对于生长中的气核,R-P 方程可表示为

式中,和依次为气核半径、气核壁面速度和气核壁面加速度;Pv为饱和蒸汽压力;S为表面张力;下标0 表示初始条件,则气核初始平衡压力Pg0可如下计算

此外,Tomita 等[44]的研究还指出: 在泡溃灭过程中,由于其表面向内收缩的速度较大,整个过程在极短的时间内完成,因此需要考虑液体的可压缩效应.因此,对于溃灭过程中的气核,R-P 方程可表示为

其中,ε=1-ρg/ρl为常数,c0为声速.比热比γ在气核生长与溃灭过程中取值不同

这是由于生长过程相较于溃灭过程进展更加缓慢,可看作等温过程,因此取γ=1;而空化泡在离开低压区进入高压区时便迅速溃灭,其表面向内收缩的速度较大,整个过程在极短的时间内完成,可将汽泡溃灭过程看作绝热过程,因此取γ=1.4[44-45].

另外,泡壁压力Pr=R可由其一阶修正估计如下

其一阶导形式为

紫杉醇近年来被广泛应用于乳腺癌、卵巢癌和宫颈癌等恶性肿瘤治疗。但由于其过敏反应发生率较高，占39%，其中严重过敏反应发生率为2%，从而使治疗被迫中止，这样不仅影响了患者治疗，而且造成经济上严重损失。2010年1月—2011年4月我院门诊输液中心肿瘤患者在接受紫杉醇治疗过程中发生了多例过敏反应，其中34例过敏反应者，经对症处理与抗过敏治疗后，继续输注紫杉醇药液，顺利完成了化疗疗程。现将临床观察与护理报道如下。

需要指出的是,气泡压力Pencounter是用表面平均法计算[27],并非由核心位置决定.这是由于如果气泡压力也采用核心压力,那么一旦气核达到梢涡旋转轴处将会无限制生长,不符合实际物理规律.而泡表面液体压力平均值这一概念的引入很好地解决了这一模型缺陷,使得在存在强压力梯度的流动条件下对气泡动力学的模拟更加真实可靠.而模型中的其他拉格朗日量是由核心位置决定的,处于核心位置的拉格朗日量是由公式计算得到

其中,φL和 φE分别表示拉格朗日框架和欧拉框架中的流动量,r表示从气核当前所在的网格中心到气核中心的距离矢量.

我们通过自编程的方式实现对每个气泡的位置、速度、感知压力和直径等气核相关变量的求解和输出.为了降低数值误差,采用4 阶Runge-Kutta 的离散格式求解离散相微分方程.此外,为了更加准确地更新离散相信息,本文采用的拉格朗日场时间步长远小于欧拉场时间步长,两者相差为104级别[41].在每个欧拉时间步结束后,开始求解拉格朗日框架,其流程如图1 所示.

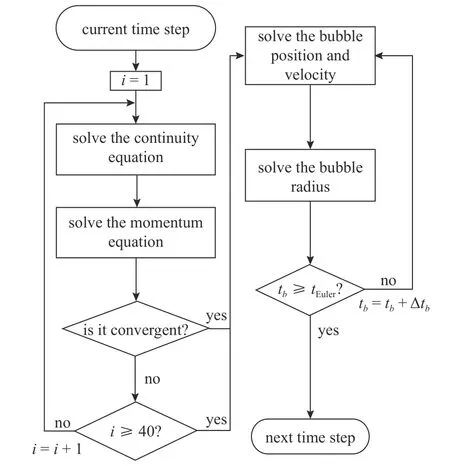
图1 考虑气核演变的空化初生预报模型求解流程Fig.1 Solution process of cavitation inception prediction model considering nuclei evolution

3 模型与计算设置

计算对象为均匀来流中的五叶右旋PPTC 模型桨,其关键几何参数如表1 所示.

表1 PPTC 模型桨几何参数Table 1 Main geometric parameters of PPTC model propeller

采用滑移网格将计算域分成静止域和旋转域两部分.速度进口和压力出口与桨盘面距离分别为4D和10D,侧面边界距离螺旋桨中心的距离为2.5D,如图2 所示.桨叶表面采用不可滑移壁面条件,其余壁面均采用自由壁面条件.螺旋桨每旋转0.1°所需的时间设置为非定常计算的时间步.

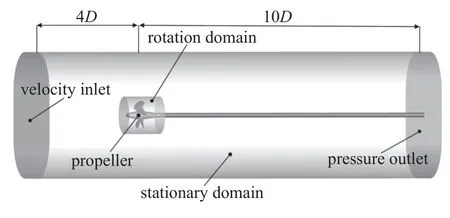
图2 计算域Fig.2 Computational domain

整个计算域主体采用切体正交网格并在叶片表面设置多层边界层以确保绝大部分桨叶表面的Y+值在5 内,满足计算要求.值得注意的是,梢涡涡心低压和径向较大的压力梯度是气核能否被梢涡捕获的关键.因此,有必要在梢涡区域进行体加密以确保能有效减小数值离散误差,准确模拟梢涡涡心低压和径向较大的压力梯度.为此,我们对粗、中和细3 种不同的梢涡体加密方案进行了网格无关性验证.图3所示的是在初生工况下距离桨中心下游0.1D处梢涡压力系数云图,可以发现相较于粗糙加密的网格,中度和精细体加密的网格均能很好地模拟出涡心低压及压力在径向上的变化.并且采用中度体加密的网格在涡心直径上分布有32 个节点,完全满足前人研究中所提到的超过16 个节点的要求[46].综上,虽然进行精细体加密的网格对涡心低压模拟得更好,但是精细化加密的网格数量太过于庞大.为平衡计算资源和计算精度最终采用中度体加密的方案进行网格生成.最终网格数量为1.357×107左右,具体网格细节和初生工况下桨叶表面Y+值分布如图4 所示.

图3 压力系数及网格分布Fig.3 Pressure coefficient and grid distribution

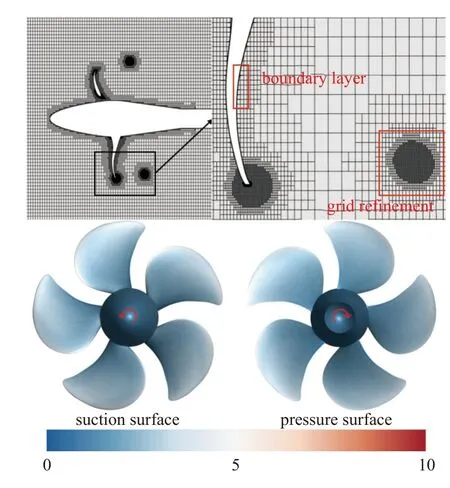
图4 网格细节和桨叶表面Y+分布Fig.4 Mesh detail and Y+ distribution on blade surface

根据文献[47]实验中梢涡空化初生工况进行欧拉流场模拟,即进速系数J=0.9983,σn=6.39,转速为131.85 rad/s.其中进出口边界条件分别由以下公式得出

根据该工况下实验给定的气核谱,在距离桨盘面上游0.2R～1.0R环状区域内随机释放初始直径分别为10 μm,20 μm,60 μm,70 μm 和100 μm 共计28800 个气核.各尺寸气核数量占比如图5 所示,气核初始释放区域如图6 所示.

图5 初始气核的尺寸分布情况[47]Fig.5 Size distribution of initial nuclei[47]

图6 气核释放区域示意图Fig.6 Diagram of nuclei release position

4 讨论与分析

4.1 模型可靠性验证

参考文献[47]实验数据对敞水性能进行预报,并将预报结果与实验对比.推力系数KT和扭矩系数KQ分别由公式给出

如图7 所示,推力系数和扭矩系数的数值模拟结果与实验结果高度吻合,且相对误差均在3%以内.这说明基于该套网格的欧拉流场的数值模拟是相对准确可靠的,这为后续离散相模拟提供了一定的基础.

图7 敞水特性Fig.7 Open water characteristics

气泡迁移方程通过对气核在理想的Rankine 涡流场[48]中的运动轨迹进行求解验证.Rankine 涡的切向速度及压力分布如下

其中,rv表示到涡心的径向距离,a表示涡核半径,Γ表示涡环量,P∞的数值由Rankine 涡的空化数决定

式中,Uc为涡核半径处的最大切向速度.本文验证了3 种不同大小尺度的气核在Rankine 涡下被捕获的过程.如图8 所示,本文所采用的模型模拟结果与文献[40]给出的结果高度吻合,证明本文采用的模型在求解气核运动方面的可靠性.

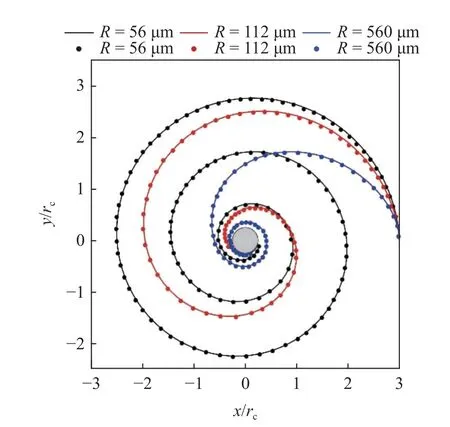
图8 3 种不同半径的核在Rankine 涡流中的运动轨迹(实线: 当前模型;散点: Zhang 等[40]的数值结果)Fig.8 The trajectories of nuclei with three different radii in the Rankine vortex flow (solid line: the current model;scatter: the numerical results of Zhang et al.[40])

气泡脉动方程则是基于Ohl 等[49]的实验结果进行验证.Ohl 等[49]测量了初始半径为8 μm 的单泡在正弦变化的环境压力下的半径变化

如图9 中与实验对比的结果可以看到,在一个压力变化周期中,模拟的气核经历了暴发式生长和迅速溃灭并多次回弹的过程,该过程与文献[50]的结果一致.此外经与实验结果对比发现,本文所采用的考虑水相可压缩效应的气泡控制方程所得到的结果相较于不考虑水相可压缩效应的结果在回弹及溃灭过程中更加准确,预测出的溃灭后的半径最小值也与实验值更加接近,这与现有的研究结论吻合[39].

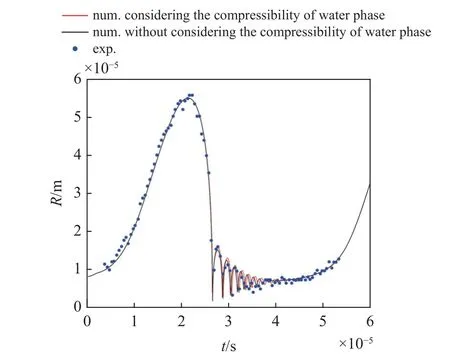
图9 实验测量[49]与数值模拟的单泡半径振荡Fig.9 Experimental measurment[49] and numerical simulation of single bubble radius oscillation

基于上述验证结果,可以认为本文所采用的离散相单泡模型可以很好地对梢涡流场中气核的运动轨迹和生长溃灭过程进行求解.

4.2 结果讨论与分析

在模型实验中,常通过观察叶片尾流中有无细小空穴的出现这种光学准则来判断空化初生.如图10展示了梢涡空化初生工况下数值模拟结果与实验的对比图.其中图10(a)展示的是基于欧拉框架下传统的ZGB 空化模型计算得到的蒸汽体积分数为0.1 的等值面,图10(c)展示的是运用本文所提的基于欧拉-拉格朗日框架下数值预报方法得到的结果.为方便观察,图10 中气泡按照实际直径的10 倍进行放大后展示.

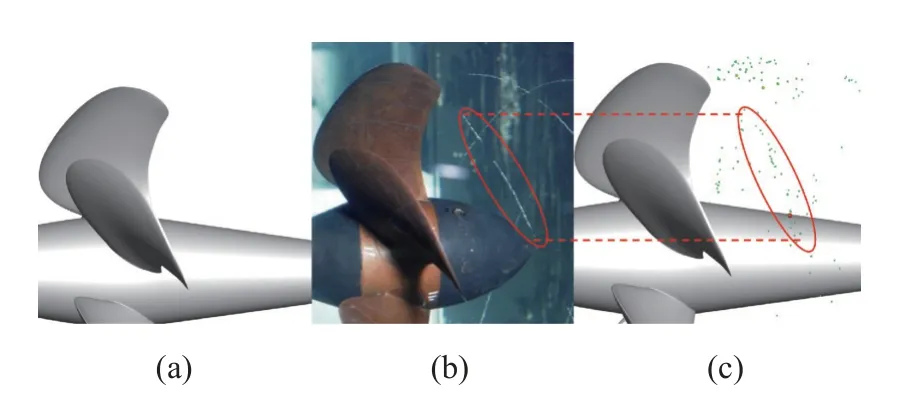
图10 试验[47]与数值模拟的初生空化对比Fig.10 Comparison of inception cavitation between experiment[47] and numerical simulation

可以清楚地看到运用本文所采用的数值方法预报的初生空化的位置与形态和同工况下实验所拍摄到的结果高度吻合.相比之下传统欧拉框架下的空化模型则完全无法准确预报这一初生空化过程,这进一步说明本文所采用的方法对于螺旋桨空化初生的预报具有明显优势,是准确可靠的.

水中气核在梢涡涡心处低压和径向方向较大的压力梯度的作用下容易被卷入涡心从而快速生长形成梢涡空化,水中来流气核尺寸是影响梢涡空化初生的重要因素,值得探讨.此外,空化初生的判别标准也是不可忽视的因素之一,有必要从微观气核尺度对空化初生的判别标准进行说明.在许多实验研究[51]中就已经给出了针对气泡动力学的空化初生判别准则,即空化初生通常由气核增长到一个阈值大小来定义.早在20 世纪Hsiao 等[24]的研究中认为气核直径增长到可观测的1 mm 即判定空化初生,在本研究中我们采取同样的光学判别准则.考虑到初始气核的最大直径与最小直径相差过大,在此一同做出最大直径超过0.5 mm 和2 mm 这两种不同的判别标准作为对比参考,以尽可能排除初始气核尺寸相差较大的影响.

图11 展示了经历暴发式生长的气核占释放的各初始尺寸气核数量的百分比.可以看到,经历暴发式生长的气核占比总体随着初始气核直径的增大而升高.这说明较大尺寸的气核更容易被梢涡捕获而生长发育成初生空化泡,与现有基于成核理论的空化研究结论相符合[52].值得注意的是,虽然不同初始尺寸的气核被梢涡捕获的难度不同,但是被捕获后生长溃灭的规律基本无异.即气核在受到梢涡作用后直径小幅度剧烈波动(如图12 黑色虚线框)后迅速暴发式生长至最大值,随后迅速溃灭,如图12 所示.

图11 经历暴发式生长的气核比例Fig.11 Proportion of nuclei experiencing explosive growth

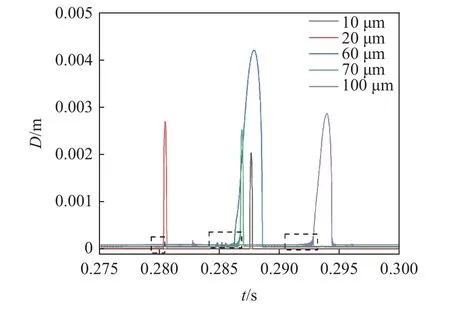
图12 不同气核暴发式生长尺寸变化Fig.12 Diameter change of nuclei experiencing explosive growth

为进一步深入探究气核被梢涡捕获后的运动状态、生长溃灭过程以及噪声特性,有必要结合流场对在梢涡作用下的典型气核生长溃灭效应进行详细分析.现有研究表明采用数值方法直接预报空化流动噪声是相当困难的[53-54].因此,我们基于气泡表面振动引起的发声机制将每个空化气泡简化为一个单极子[55-56],每个气泡产生的噪声用单极噪声源进行建模[57],单个气泡产生的声压如下表示

式中,Vb为气泡体积,R是气泡半径,r为气泡到接收器的距离,为方便计算在此设为1 m.

由图13 展示的气核所感知的周围环境压力系数、气核半径变化及其产生声压的变化曲线可以看出,气核的生长和初生空化泡的溃灭都会引起噪声的增强,尤其是溃灭过程,其噪声表现为较强的声压脉冲,会大幅提高远场的噪声强度.相比之下,在气核生长至最大尺寸的过程中,声压则呈现波动状态且幅值较低.

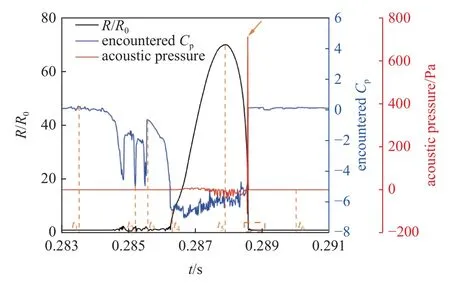
图13 典型气核尺寸、感知压力系数和声压变化曲线Fig.13 Typical nuclei size,encountered Cp and acoustic pressure change curves

为详细分析气核所处流场中与梢涡的相对位置对其演变过程的影响,从而进一步揭示初生空化在螺旋桨梢涡流场中的发声机制,本研究选取了气核在梢涡作用下生长到溃灭过程中t1～t66 个典型时刻,展示了气核被梢涡卷入涡心并随后离开梢涡的典型过程,如图14 所示.为方便观察,图中除尺寸最大的t5时刻的气核按照实际半径展示,其余时刻均按照实际尺寸10 倍放大后进行展示,灰色半透明等值面为Q=2.5×105s-2等值面,以表征梢涡形态.

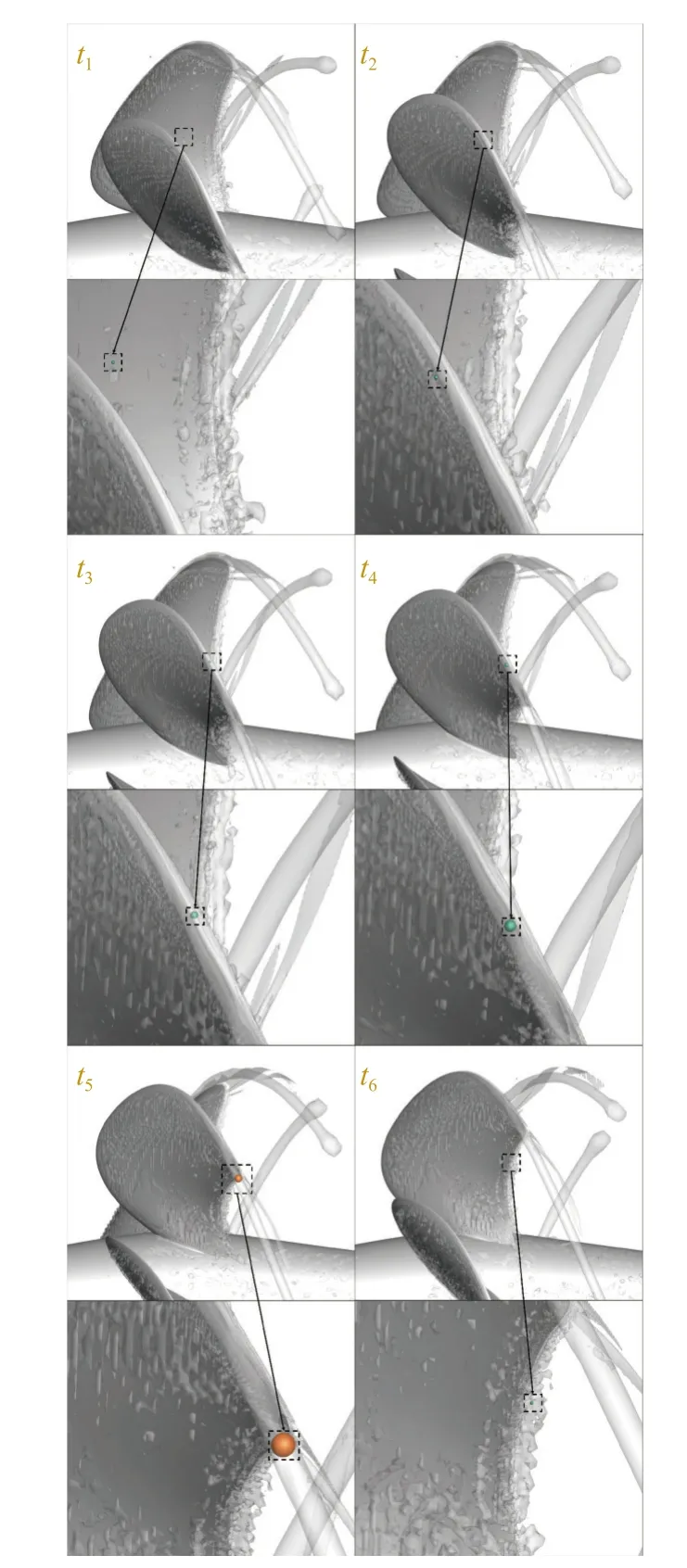
图14 典型粒子与涡的相对位置Fig.14 Relative position of typical nuclei and vortex

结合图13 可以看到在t1～t3时刻,在叶梢附近气核在梢涡卷吸的作用下开始向梢涡核心靠近且半径在小范围内波动,直到t3时刻被进一步卷吸到梢涡边缘附近.此阶段并未产生明显的声压信号.这是由于气核在梢涡卷吸的作用下逐渐靠近梢涡边缘但并没有进入到涡心低压区,如图13 蓝色曲线所示的气核感知压力虽然有明显的降低但很快便回升,低压作用时间不长,气核尺寸因此也并未出现暴发式生长的现象.

随后的t3～t4时刻,气核在梢涡径向压力梯度的影响下进一步向涡心低压区靠近,气核周围环境压力逐渐降低.值得注意的是,在t4时刻附近,气核在涡心低压的作用下半径波动更加剧烈,峰值不断抬高,但由于刚进入涡心低压区,低压作用时间不长,气核尺寸整体并未有较大增长.气核在t4时刻进入涡心低压区后,气核周围压力一直在较低范围内小幅剧烈波动,气核持续受到涡心低压的作用,开始呈现暴发式生长,直到t5达到最大值.此阶段由于气核体积的快速增大而产生声压低频波动状态的声压信号,但是声压等级并不高且基本为负值.随后气核被迅速甩出梢涡核心低压区,气核周围压力迅速回升至较高的初始水平附近,初生空化泡迅速收缩溃灭,并释放出一个较强的声压脉冲信号,如橙色箭头所示.气核暴发式生长后被甩出梢涡核心低压区这一过程可能与气核暴发式生长后气核尺寸快速变大而阻力随之增大密切相关,但未有精细的实验测量和深入研究,具体物理机理仍尚不明确,值得进一步深入研究.

此外值得注意的是,气核在暴发式生长并溃灭后并没有立即恢复至初始大小,而是有小幅回弹的过程,如虚线框中的半径变化曲线所示.这是由于气核中含有的不可凝结气体会阻止其完全溃灭,从而出现小幅回弹[40],并在回弹过程中造成持续的较小幅值的噪声.

可以看出气核伴随水流向下游运动的过程中受到梢涡卷吸的影响,其在生长和溃灭的过程与梢涡密切相关,这说明涡心流动特性对气核演变及其产生的声压水平产生重要影响.

5 结论

本文发展并采用基于气泡动力学方程的欧拉-拉格朗日框架下的梢涡空化初生数值预报方法对PPTC 桨梢涡空化初生进行了准确的数值预报并从微观气核角度进行了分析研究.得到主要结论如下.

(1) 采用本文考虑水相可压缩效应的欧拉-拉格朗日数值预报方法能够对螺旋桨梢涡初生空化进行准确的模拟.

(2) 来流气核尺寸对螺旋桨梢涡空化初生有着显著影响.在光学判别标准下较大初始尺寸的气核更容易被梢涡捕获而生长发育为初生空化泡,但不同初始尺寸气核被梢涡捕获的生长溃灭规律基本一致.

(3) 气核在梢涡卷吸的作用下靠近涡心低压区时,气核感知压力短暂地大幅度波动;气核开始进入涡心低压区后,感知压力快速降低,随后小幅度剧烈波动,且整体呈缓慢上升趋势.最终,气核在涡心低压的持续作用下开始暴发式生长直至尺寸达到最大.

(4) 气核进入涡心低压区后,声压开始小幅低频波动,且基本为负值;待尺寸达到最大值后气核迅速收缩溃灭,同时产生最强的正声压脉冲信号.