不同收缩口模中聚合物熔体流变行为的数值模拟

刘庆升,刘友琼,柯春海

(信阳师范大学 数学与统计学院, 河南 信阳 464000)

0 引言

随着黏弹本构方程和模拟技术的发展,准确刻画聚合物熔体的流变特性成为可能。数值模拟作为一种描述和预测黏弹流体流变性的重要方法,成为聚合物加工工业中的一种重要的设计辅助工具。

一直以来,人们都希望能够对复杂流体尤其是聚合物熔体的非线性动力学行为进行准确刻画。为此发展了一系列的黏弹本构方程,包括PTT模型[1]、Wagner模型[2]、Doi-Edwards模型[3]、Pom-Pom模型[4]、Rolie-Poly模型[5]以及相应的改进模型[6],并将这些本构模型应用于非牛顿流体力学的研究[7-9]。上述模型各有优缺点,根据聚合物分子链的特征,Rolie-Poly模型适宜描述线型聚合物熔体的流变特征,而Pom-Pom模型适宜描述分支型聚合物熔体的流变特征。

聚合物在复杂的加工成型条件下常牵扯到熔体的流动与变形,这与收缩流中复杂流体的流动类似。因此,收缩流常作为基准流动用于研究聚合物熔体的流变行为[10-13]。HASSELL等[14]基于实验研究了不同类型的聚苯乙烯熔体在收缩扩张型腔中的流变行为,详细讨论了收缩口的曲率、熔体的流率对流动不稳定性的影响。COMBEAUD等[15]通过挤出成型实验研究了口模的收缩角对流动双折射的影响,并得出了制件表面缺陷受到收缩角强烈影响的结论。AGASSANT等[16]详细综述了聚合物熔体挤出成型过程的流动不稳定的实验后发现,这些挤出不稳定是影响挤出生产线最大输出量的关键因素;作者还详细总结了影响收缩流中挤出不稳定的可能因素,并提出了消除或尽可能减少这些挤出不稳定的方法。AGASSANT等[17]简要综述了聚合物加工在工业、实验研究及模型研究的发展现状,同时指出了精确地预测聚合物熔体的流变行为一直是一个挑战。

在挤出成型中,聚合物熔体在收缩口附近往往会产生应力集中现象,该现象会导致熔体破裂以及最终制件出现鲨鱼皮型的表面缺陷。本文的主要目的是基于有限体积法和Rolie-Poly本构模型研究聚苯乙烯熔体在收缩口模中的流变行为,探究在不同收缩长度的条件下V-型收缩口模及喇叭型收缩口模对聚苯乙烯熔体流变性的影响,同时给出流场中有关主应力差、剪切力、伸展率等更多更详细的信息,能够更好地理解聚合物熔体进入收缩口时的动力学响应过程。

1 数学模型

1.1 质量和动量守恒方程

基于不可压缩及等温条件,对聚苯乙烯熔体流变性进行研究,同时不考虑表面张力的影响。因此,质量和动量守恒方程可以写成如下的形式:

∇·u=0,

(1)

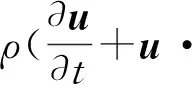
(2)

式中:u、σ分别表示速度矢量和应力张量,ρ、p及ηs分别表示熔体的密度、压力及溶剂的黏度。

1.2 Rolie-Poly本构方程

Rolie-Poly本构方程,常用该模型来描述线型聚合物熔体的应力-应变状态,其形式为

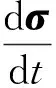
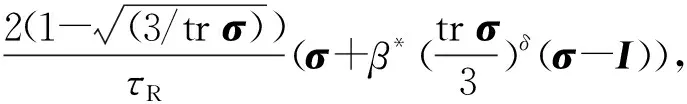
(3)

1.3 动量方程及Rolie-Poly本构方程的无量纲形式

数值结果将采用无量纲形式来表示,定义U和L分别为速度和长度尺度,则动量方程和Rolie-Poly本构方程的无量纲化可通过式(4)得到

(4)

动量方程的无量纲化形式为:

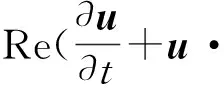
(5)

式中:Re=ρUL/η表示雷诺数,η=ηs+ηp为总黏度,β=ηs/(ηs+ηp)为溶剂黏度与总黏度的比值,ηp表示聚合物黏度。

Rolie-Poly本构方程的无量纲化形式为:

(1-β)(∇u+(∇u)T)-

(6)

式中:τ=We/(1-β)·trσ+trI,We=τdU/L和WeR=τRU/L分别为基于链的取向和伸展松弛时间所定义的Weissenberg数。

1.4 边界条件

速度矢量u和应力张量σ的入口边界条件为

u=uinflow,

(7)

σ=0。

(8)

出口边界采用齐次Neumann边界条件:

(9)

(10)

式中:n表示出口的熔体的流出方向。

固壁采用无滑移边界条件,相应的应力张量可以由方程(6)推导得到,可参阅文献[12],在此不再赘述。

1.5 流动诱导双折射

聚合物熔体的流动诱导双折射可以通过偏光弹性仪得到,这种现象产生的原因是应力的各向异性引起了光折射率的各向异性。实验观测到的双折射与模拟得到的主应力满足应力光学定律,即

△n=c△σ,

(11)

式中:△n表示双折射;△σ表示主应力差;c为常数,又称为应力光学系数。对于二维情况,△σ的形式为

(12)

2 数值方法

基于同位网格有限体积法对质量守恒方程、动量守恒方程和Rolie-Poly本构方程进行离散,并采用SIMPLE算法[18]进行求解。

在控制体内对质量守恒方程进行积分,可得到其离散形式

(ue-uw)△y+(vn-vs)△x=0,

(13)

式中:uw和ue分别表示控制单元左侧和右侧界面上x方向的流率,vn和vs分别表示控制单元上侧和下侧界面上y方向的流率,△x和△y分别表示x和y方向上的网格步长。

以同样方式对动量方程进行离散,对流项采用中心差分格式,可得

aPuP=aEuE+aWuW+aNuN+aSuS+S(u),

(14)

式中:S为动量方程的源项,系数aP、aE、aW、aN、aS与对流项和扩散项密切相关,其形式为

aE=DeA(|Pe|)+max(-Fe,0),

aW=DwA(|Pw|)+max(-Fw,0),

aN=DnA(|Pn|)+max(Fn,0),

aS=DsA(|Ps|)+max(Fs,0),

aP=aE+aW+aN+aS+ρ△x△y/△t,

式中:De、Dw、Dn、Ds为单元面上的扩散系数,Pe、Pw、Pn、Ps为单元面上的Peclet数,Fe、Fw、Fn、Fs为单元面上的通量,对流项的离散采用中心差分格式A(|P△|)=1-0.5|P△|。上述系数的表达式为

Fe=ρue△y,De=η△y/Re(xE-xP),Pe=Fe/De,

Fw=ρuw△y,Dw=η△y/Re(xP-xW),Pw=Fw/Dw,

Fn=ρvn△x,Dn=η△x/Re(yN-yP),Pn=Fn/Dn,

Fs=ρvs△x,Ds=η△x/Re(yP-yS),Ps=Fs/Ds。

本构方程的离散形式可类似得到。

3 数值结果

所采用的聚合物材料为巴斯夫公司提供的聚苯乙烯(代号为PS2)。数值模拟基于单模式的Rolie-Poly本构模型描述聚苯乙烯熔体在不同收缩口模流动过程中的应力-应变关系,熔体温度设为200 ℃。首先,基于4∶1收缩流验证模型及算法的有效性;接着,讨论在不同的收缩长度L下,V-型收缩口模及喇叭型收缩口模对聚苯乙烯熔体流动的影响。当收缩长度L=0时,此时型腔为4∶1突然收缩型腔,如图1(a)所示。

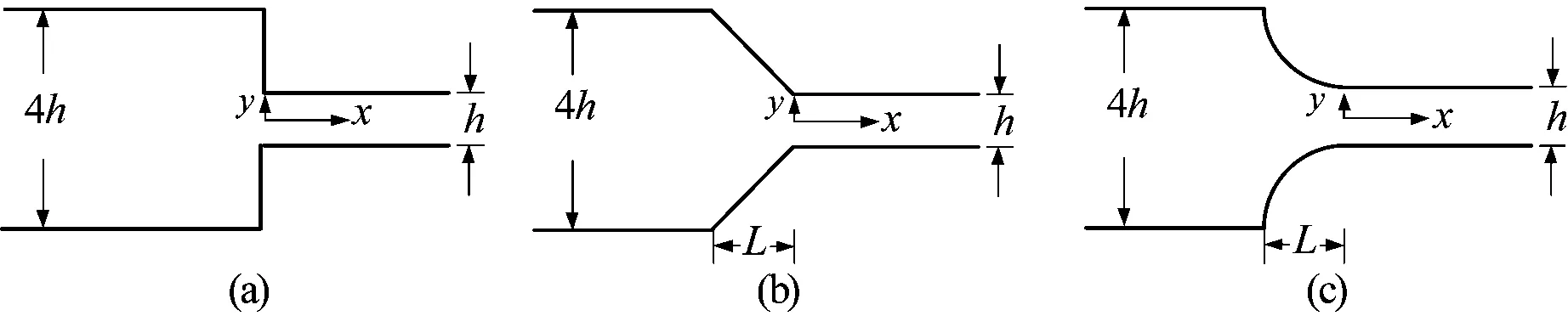
图1 4∶1收缩口模示意图(a)突然收缩口模;(b)V-型口模;(c)喇叭型口模Fig. 1 Schematic diagram of 4∶1 contraction dies (a) Abrupt contraction; (b)V-shaped contraction; (c) Trumpet-shaped contraction

当收缩口为V-型口或喇叭口时,如图1(b)和图1(c)所示,为了保证数值算法的顺利实施,采用区域扩充法[18]将计算区域扩充为图1(a)所示区域。计算区域的直角坐标系如图1所示,计算过程中采用的网格为均匀网格△x=△y=0.025。本文算法基于Visual C++语言在3.6 GHz的酷睿i7-4790处理器上实现。

3.1 模型及算法验证

收缩流常用于挤出成型和注射成型等聚合物加工领域,高剪切和高拉伸的流动分别出现在模壁附近及收缩口附近区域,收缩流能更好地反映聚合物流体的物理特性,而4∶1突然收缩流常作为基准算例。选用文献[10]中的算例验证模型及算法的有效性以及Rolie-Poly本构方程刻画聚合物熔体应力-应变关系的能力。主要目的是基于上述模型和算法研究收缩口的不同外形对聚苯乙烯熔体流变行为的影响,下面仅简要给出验证性结果。图2为不同流率下聚苯乙烯熔体在4∶1突然收缩口模中的双折射实验及模拟结果对比图,其中图2(a)—(c)分别对应的流率为1.433 3、2.866 7、4.3 mm/s,图的下半部分为实验结果[10],上半部分为本文的模拟结果。

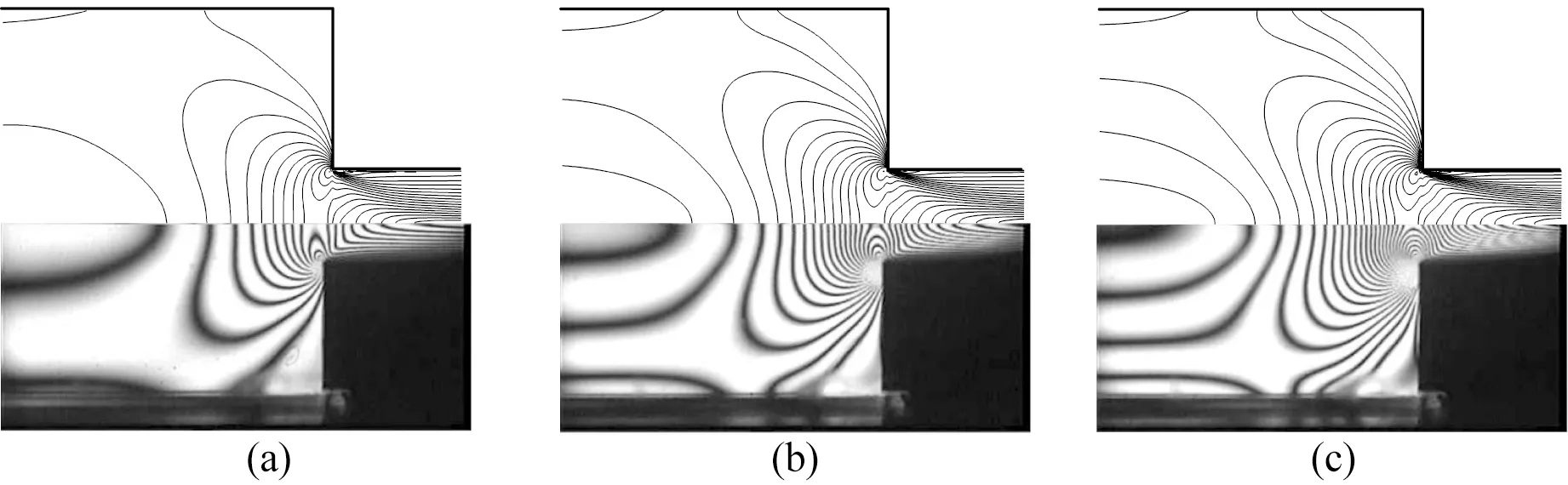
图2 不同流率下由实验[10]及模拟所得到的双折射图(a)1.433 3 mm/s;(b)2.866 7 mm/s;(c)4.3 mm/sFig. 2 Comparison between experimental and predicted birefringence for PS2 melt at different flow rates(a) 1.433 3 mm/s; (b) 2.866 7 mm/s; (c) 4.3 mm/s

从图2可以看出,当流率为1.433 3 mm/s时,所预测的条纹数与实验是相同的,而在高流率时,预测出的条纹数比实验测的条纹数略少。众所周知,对黏弹流体流变性的准确预测一直是个难题,为了更准确地描述黏弹流体的流动和变形特性,人们一直在不断地改进已有本构方程及相应算法。总体来说,本文预测的双折射结果与实验结果基本上是一致的,能够反映聚苯乙烯熔体在收缩流中的流变性,同时说明了本文的模型及相应的求解算法的有效性。

3.2 V-型收缩口模对聚合物熔体流动的影响

本节主要研究V-型收缩口模在不同收缩长度条件下对流动的影响。图3为本文预测的V-型收缩口模在不同收缩长度条件下沿入口和出口中心线上的主应力差、第一法向应力差、伸展率以及速率。

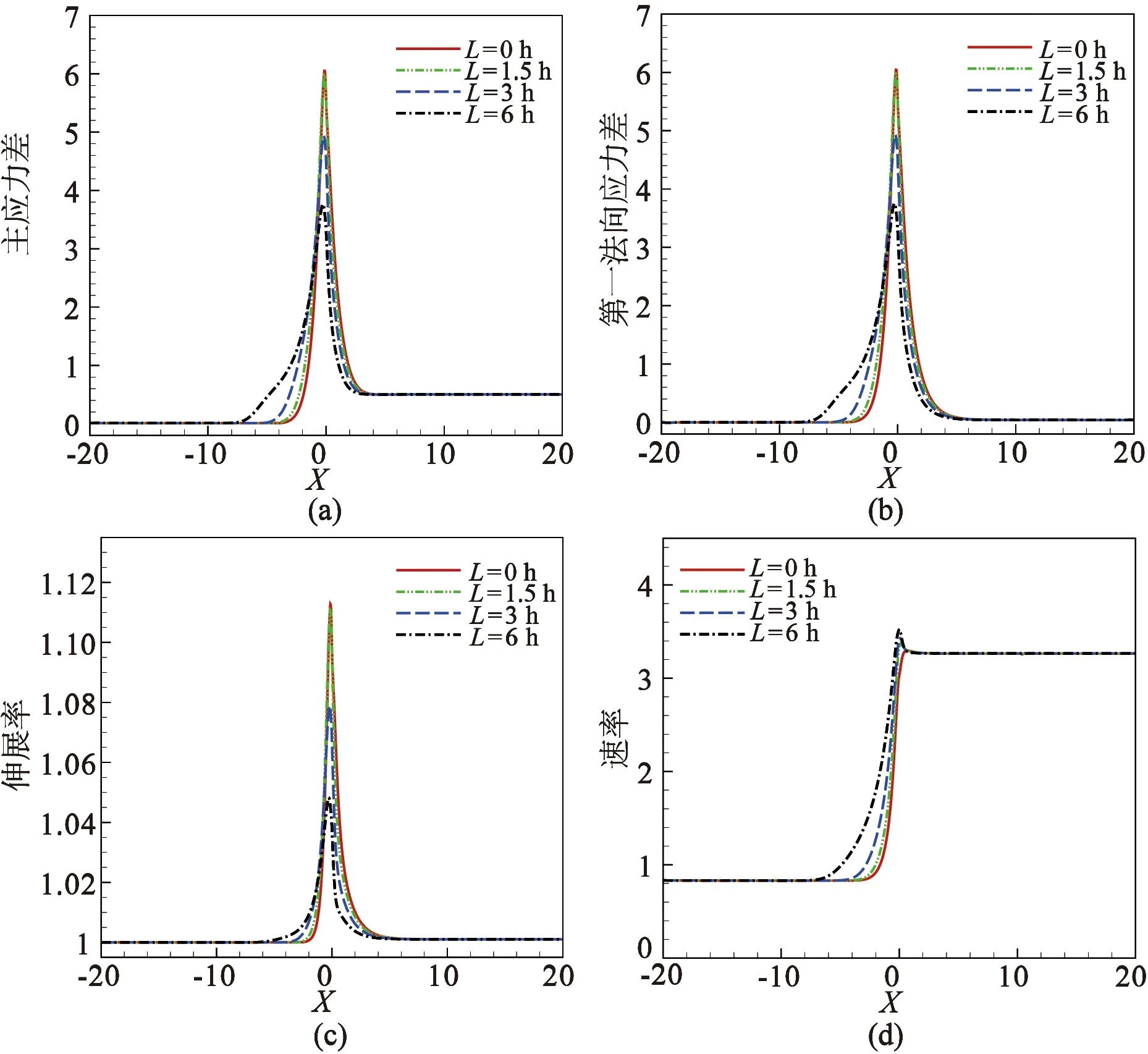
图3 本文预测的不同收缩长度的V-型口模沿型腔中心线上的主应力差、第一法向应力差、伸展率和速率Fig. 3 The present simulation results of principal stress difference, first normal stress, stretch ratio and velocity along the centerline of V-dies with different contraction length

从图3可以看出,随着收缩长度的变化,这些量在远离收缩口的上游和下游区域并没有发生变化,而在收缩口区域附近发生了明显的变化。主要原因可解释为:在远离收缩口的上游区域,流场的变化趋势是相对平稳的,对聚合物的分子链几乎没有影响,分子链的构型并没有受到扰动,仍处于平衡状态。在离收缩口一定距离的下游区域,流体流动充分发展,聚合物分子链达到了完全松弛状态,相应的物理量不发生变化。而当流体流经收缩口及其附近区域时,分子链受到了较强的剪切和拉伸影响,相应的物理量在此区域变化强烈。随着收缩长度的变大,主应力差、第一法向应力差和伸展率的最大值明显降低,而速率的最大值明显增大,这也是符合理论分析的,众所周知,当流体流经收缩的流道时,截面积的减小将会导致流体速率的增大。

3.3 喇叭型收缩口模对聚合物熔体流动的影响

本节主要研究喇叭型收缩口模在不同收缩长度条件下对流动的影响。图4为本文预测的V-型收缩口模在不同收缩长度条件下沿入口和出口中心线上的主应力差、第一法向应力差、伸展率以及速率。

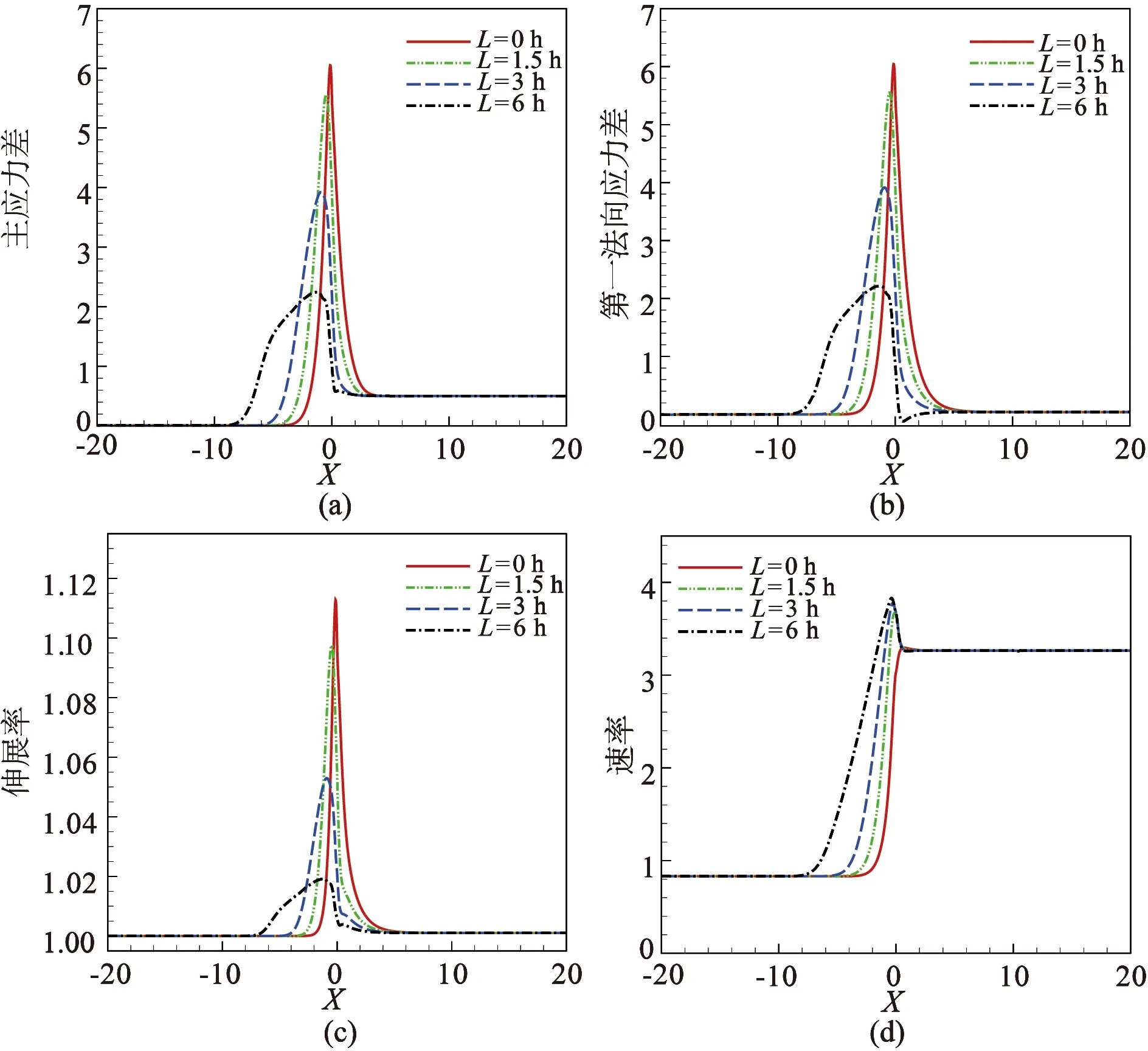
图4 本文预测的不同收缩长度的喇叭型口模沿型腔中心线上的主应力差、第一法向应力差、伸展率和速率Fig. 4 The present simulation results of principal stress difference, first normal stress, stretch ratio and velocity along the centerline of trumpet-shaped dies with different contraction length

从图4可以看出,主应力差、第一法向应力差、伸展率和速率的变化趋势与V-型收缩口模的情况类似,随着收缩长度的变大,主应力差、第一法向应力差和伸展率的最大值明显降低,而速率的最大值明显增大。从图3和图4容易看出,在相同收缩长度的条件下,喇叭型的收缩口模中聚合物熔体的主应力差、第一法向应力差和伸展率要比V-型口模中的更小,而速率更大。所以相对于突然收缩口,采用V-型口模或喇叭型口模都将会减小收缩口附近的应力集中现象(应力的局部增高),而喇叭型口模的效果更好,能够更大程度地减小应力集中现象,从而能够减小挤出成型中由应力集中导致的制品表面缺陷。

4 结论

主要研究了不同收缩长度下的V-型和喇叭型口模对聚苯乙烯熔体流变性的影响。数值结果表明:(1) 本文所采用的数值方法和算法切实有效,Rolie-Poly模型能够刻画聚苯乙烯熔体的流变特征,这也是复杂流体可计算建模的一次成功实践;(2)相对于突然收缩流,具有V-型和喇叭型收缩口的型腔能够有效减小流场中的主应力差、第一法向应力差和伸展率,而喇叭型收缩口减小的效果更好;(3)不论是V-型还是喇叭型收缩口模,随着收缩长度的增大,聚苯乙烯熔体在收缩流中的主应力差、第一法向应力差和伸展率都具有明显的下降趋势;(4)在挤出成型中,为尽量减少或避免由应力集中导致的制件表面缺陷,应尽可能选择具有喇叭型外形且具有尽可能长的收缩长度的口模。