具有公共卫生教育影响和 Lévy跳的随机SEIS传染病模型的动力学行为分析

师向云, 周 丹, 张泰瑞, 陆 路

(信阳师范大学 数学与统计学院, 河南 信阳 464000)

0 引言

面对新冠肺炎疫情的严峻形势,公共卫生教育已成为一种控制传染病传播的有效措施,尤其对于贫困地区以及一些信息传播极度滞后的封闭区域,更需要加强对其进行公共卫生教育的力度[1]。最近几年,关于公共卫生教育对传染病影响的数学模型演变出很多类型[2-6],但它们大多是确定性模型,实际上环境干扰对流行病模型的影响不可忽略,因此有必要研究环境噪声对传染病数学模型的影响。噪声包括常见的白噪声和强度较大的Lévy跳跃噪声[7-8]。考虑到在传染病发生的偏远山区或贫困区域,常伴有地震、洪涝、火山爆发、干旱等突发性且强度较大的随机干扰,引入Lévy跳过程可以更加准确地描述环境所带来的扰动。因此本文建立一类具有公共卫生教育影响的随机传染病模型来讨论疾病消失和持久的条件,所建模型如下:

(1)

式中:S(t)、E(t)、I(t)分别表示t时刻易感者、受教育者和感染者的种群密度;βSI为疾病传染率,β是疾病传播的有效接触率;1/(1+piI)(i=1,2)表示易感个体数量增加时的行为变化或感染个体的拥挤效应和抑制效应,p1、p2≥0代表饱和传染率系数;参数Λ表示进入到易感人群的比率;ε表示公共卫生教育战略在易感人群中传播的速度;γ表示感染者的恢复率;σ为疾病死亡率;μ为各个种群的自然死亡率;由于采取教育控制措施的力度会逐渐减弱,假设受教育者以αβEI(0<α<1)概率被感染,其中α是教育减少感染的比例系数。

定义(Ω,F,{F}t≥0,P)是一个完备的概率空间,且{F}t≥0是这个概率空间的满足通常条件的滤子。Bi(t)(i=1,2,3)表示概率空间上相互独立的标准布朗运动,σi>0(i=1,2,3)表示环境白噪声强度;记

N是在(0,+∞)×Z上的泊松计数测度,λ是可测子集Z上N的特征测度,满足λ(Z)<+∞;S(t-)、E(t-)、I(t-)分别是(S(t),E(t),I(t))的左极限,γi(u)(i=1,2,3)表示Lévy跳跃强度。

为方便计算,假设:

(A1) 对于任意的N>0,存在LN>0,使得跳跃扩散系数满足

LN|x-y|2,|x|∨|y|≤N,

式中:Hi(x,u)=γi(u)x(t-),(i=1,2,3)。

(A2) 对于1+γi(u)>0(i=1,2,3),有

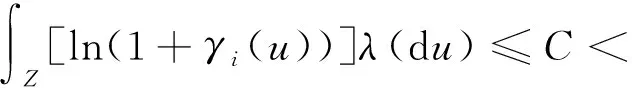
式中:C是一个正常数。

1 全局正解的存在唯一性

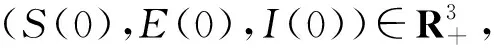
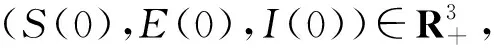
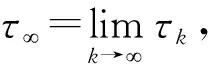
下面使用反证法证明。假设存在常数T>0和ε∈(0,1),使得P{τ∞≤T}>ε,则存在一个整数k1≥k0,使得对任意k≥k1,都有

P{τk≤T}≥ε。

(2)

(E-1-lnE)+(I-1-lnI),

式中:b是待定的正常数,且函数的非负性可以从u-1-lnu≥0(u>0)得出。

对函数V利用It公式,可得

dV=LVdt+σ1(S-b)dB1(t)+

σ2(E-1)dB2(t)+σ3(I-1)dB3(t)+

式中:

[γ2(u)-ln(1+γ2(u))]+

[γ3(u)-ln(1+γ3(u))]λ(du)≤

这里

选取b=(μ+σ)/β,使得bβ-μ-σ=0,因此可得

这里K是正常数,故

dV≤Kdt+σ1(S-b)dB1(t)+

σ2(E-1)dB2(t)+σ3(I-1)dB3(t)+

(3)

对式(3)两边从0到τk∧T积分并取期望,可得

E[V(S(τk∧T),E(τk∧T),I(τk∧T))]≤

V(S(0),E(0),I(0))+KT。

令Ωk={τk≤T},k≥k1,由P{τk≤T}≥ε知,P(ΩK)≥ε,则对于每个ω∈Ωk,存在S(τk,ω)、E(τk,ω)、I(τk,ω)等于k或者1/k,于是

V(S(τk∧T),E(τk∧T),I(τk∧T))≥

从而

V(S(0),E(0),I(0))+KT≥

E[IΩk(ω)V(S(τk,ω),E(τk,ω),I(τk,ω))]≥

式中:IΩk(ω)是Ωk的示性函数。令k→∞,则有

+∞>V(S(0),E(0),I(0))+KT=+∞,

矛盾。因此τ∞=+∞ a.s.。证毕。

2 疾病的消失

记

式中:X(t)是[0,+∞)上的可积函数。

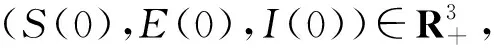
且

证明根据文献[9]中引理1的证明可以类似得到。证毕。

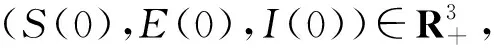
证明根据文献[9]中引理2的证明可以类似得到。证毕。

接下来给出疾病消失的条件。

式中:

则传染病I(t)消失,即

进一步可得

证明对lnI(t)运用It公式可得

(γ+σ+μ)-θ3)dt+

(4)

由基本不等式u-1-lnu≥0(u>0),可得θ3的非负性。

式(4)左右两端从0到t上积分并除以t,可得

(5)

应用公式

d(S(t)+E(t)+I(t))≤

(Λ-μ(S+E+I))dt+

σ1S(t)dB1(t)+

σ2E(t)dB2(t)+σ3I(t)dB3(t)+

对上式左右两边从0到t积分再除以t,然后取上极限,再根据引理1和引理2可得

从而

对式(5)左右两边取上极限,再利用引理1和引理2可得

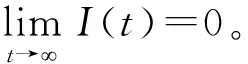
现在考虑将模型(1)中第一式与第三式相加,并对其和式两边从0到t积分再除以t,得到

(σ+μ)〈I(t)〉+φ1(t),

(6)

式中:

(7)

式中:

结合式(6)和式(7)可得

(8)

式(8)两边同时取极限,由

可知

(9)

另一方面,对于方程(1)中的第一式有

(10)

式中:

进而有

(11)

同理可得

(12)

故由式(9)有

证毕。

3 疾病的平均持久

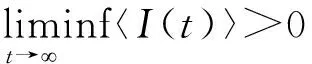
记

式中:

式中:i=1,2,3。

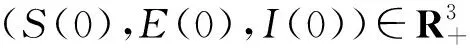
式中:

即当R2>1时,模型(1)中疾病是平均持久的。

证明定义函数H:

H(S(t),E(t),I(t))=-(a1+b1)lnS-

b2lnE-lnI,

式中:a1、b1、b2是待定的正常数。

dH=LHdt-(a1+b1)σ1dB1(t)-

b2σ2dB2(t)-σ3dB3(t)-

b2ln(1+γ2(u))+

(13)

式中:

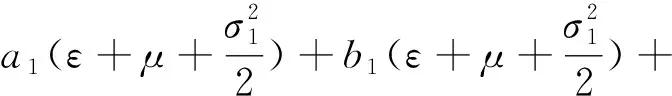
(a1+b1)βI+b2αβI+

(1+p1I)+(1+p2I)+

b2[(γ2-ln(1+γ2))+

(γ3-ln(1+γ3))]λ(du)≤

a1(ε+μ+θ1)+

b1(ε+μ+θ1)+b2(μ+θ2)+

(γ+σ+μ+θ3+2)+

[(a1+b1)β+b2αβ+p1+p2]I。

由a1、b1、b2的定义可知,

b1(ε+μ+θ1)=b2(μ+θ2)=

于是

(γ+σ+μ+θ3+2)+

((a1+b1)β+b2αβ+p1+p2)I。

(14)

对式(13)两边从0到t积分再除以t,同时结合(14)可得

-(γ+σ+μ+θ3+2)(R2-1)+

(15)

这里

(a1+b1)ln(1+γ1(u))+

根据引理1和引理2知

(16)

对式(15)两边取下极限,当R2>1时,有

证毕。

4 结论

主要研究了一类具有公共卫生教育影响和Lévy跳的随机传染病模型。通过构造Lyapunov函数,运用It公式等随机理论进行分析,证明了该模型存在唯一的全局正解,并给出了疾病消失和持久的条件。

由定理2知,当R1<1时,疾病消失,并且发现:当环境白噪声强度σ3和Lévy跳扰动强度γ3增大时,θ3也随之增大,那么R1就会减小,这表明随机扰动对疾病的灭绝有促进作用,且扰动强度越大,疾病越容易灭绝。结论表明,随机扰动对于疾病的控制具有抑制作用。

为了确定因受教育而减少感染的比率α的变化是如何影响疾病传播的,对基本再生数R2关于参数α进行敏感性分析,具体由下式给出:

这意味着α参数值的减小将导致R2的减小,也就是说α越接近0,教育在预防疾病感染上的效果越好,使得基本再生数越小,疾病感染的人数越少。这充分说明公共卫生教育对于疾病传播的影响较大,且有一定的抑制作用。