一类时空离散捕食系统的混沌与斑图转变
类维倩,郭丰路,黄头生
(华北电力大学 工程生态学与非线性科学研究中心,北京 102206)
捕食系统空间斑图形成是生态系统最基本的非线性特征之一[1],捕食系统的时空复杂性[2-3]通过斑图的多样性来体现.自1952年Turing[4]首次提出斑图研究理论,利用图灵理论研究捕食系统斑图成为捕食系统中的研究热点[5-6].近年来,基于捕食系统模型的斑图自组织格局研究越来越多[7].文献[8]研究具有强Allee效应的捕食系统模型的斑图动力学,发现捕食系统可形成点状、条纹状、孔洞状、螺旋状斑图;文献[9]研究了存在交叉扩散的捕食模型图灵斑图形成,结果表明交叉扩散可以导致多模式的斑图形成.
在捕食系统斑图自组织的研究不断发展的基础上,发现斑图自组织的形成尤其是在通往混沌路径上的斑图转变对于揭示生态系统的基本规律具有重要意义.但目前在混沌路径上的斑图研究较少,对于时空混沌斑图自组织和转变规律认识仍然不足,需进一步探索时空离散捕食系统混沌路径上的斑图特性.
本文基于Holling Ⅳ和Leslie-Gower型时空离散捕食模型,探究倍周期分岔、Neimark-Sacker分岔与图灵分岔产生的条件,以及分岔引发的混沌行为;通过数值模拟展示了混沌路径上的自组织斑图的转变规律.该研究呈现了在周期、拟周期和混沌吸引子之上由图灵失稳产生的各类混沌斑图以及斑图特性的转变,为时空离散捕食系统复杂动力学和时空复杂性研究提供了新的理解.
1 时空离散捕食系统和稳定性分析
耦合映像格子是一类时间离散、空间离散和状态连续的动力学模型,可用于刻画时空离散捕食系统的动态演化过程.基于耦合映像格子的时空离散捕食系统可以描述为[10]
(1)
(2)
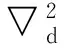
(3)
式(2)中f和g是由被捕食者和捕食者种内和种间局部相互作用所确定的函数.本文研究具有Allee效应和Holling Ⅳ功能反应函数的Leslie-Gower型捕食模型[11],如式(4)所示.其中,X和Y分别表示被捕食者和捕食者种群密度;r和K分别表示在无捕食状态下被捕食者的内禀增长率和环境容纳量;S表示捕食者的内禀增长率.为了便于理论分析,对式(4)进行无量纲化处理,得到函数f和g表达式如(5)所示,该处理不会影响时空离散捕食系统的研究结果.
(4)
(5)
其中,x(1-x)(x-m)表示被捕食者的种群增长受Allee效应影响;x/(α+bx2)表示Holling Ⅳ型的功能反应函数;cy/x表示Leslie-Gower型的数值响应函数;a、b、c、m都是正常数.在生态学意义的要求下,以上方程中所有参数取值必须为正,且x和y须为非负值.
首先进行时空离散捕食系统的局部稳定性分析.不考虑方程(1)-(3)中的空间项,将式(5)f、g的表达式代入式(2),并将所得差分方程写成如下映射表达式
(6)
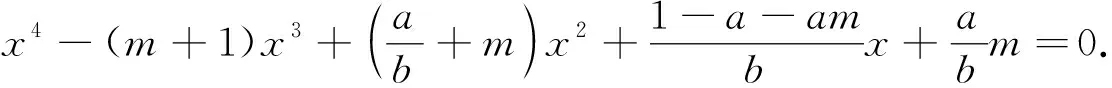
(7)
将不动点的值代入雅可比矩阵(7),计算雅可比矩阵的2个特征值λ1和λ2.当|λ1|<1和|λ2|<1时,不动点是稳定的;若|λ1|>1或者|λ2|>1,则不动点是不稳定的.对于映射(6) 3个不动点的局部稳定性分析结果如下:
1)J(1,0)的2个特征值为λ1=1+τ(m-1)和λ2=1+cτ.因λ2>1,可知不动点(1,0)是不稳定的.
2)J(m,0)的2个特征值为λ1=1+τm(m-1)和λ2=1+cτ.因λ2>1,可知不动点(m,0)是不稳定的.
3)J(x*,y*)的2个特征值为
(8)
其中,
p=-2+cτ-τ[-3x*2+2(m+1)x*-m-x*(a-bx*2)/(a+bx*2)2],
(9)
q=τ[-3x*2+2(m+1)x*-m-x*(a-bx*2)/(a+bx*2)2](1-cτ)+cτ2x*/(a+bx*2)+1-cτ.
(10)
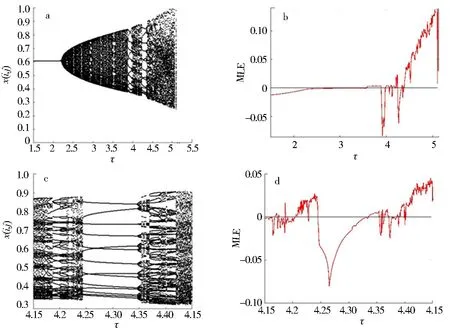
当q<1,-(1+q) 本节分析时空离散捕食系统的倍周期分岔、Neimark-Sacker分岔和图灵分岔.前2个分岔的产生不依赖于空间项,可基于映射(6)进行分析. 根据倍周期分岔定理[13]分析时空离散捕食系统的倍周期分岔及其产生条件.选择时间尺度参数τ作为控制参数,围绕不动点(x*,y*)进行分岔分析.令q=p-1,得到 (11) 其中,a0=3x*2-2(m+1)x*+m+x*(a-bx*2)/(a+bx*2)2. 在满足上述条件时,(x*,y*)的2个特征值变为λ1=-1,λ2=1-p(τ*).此外,倍周期分岔的产生需满足|λ2|≠1,即 τ*[c+3x*2-2(m+1)x*+m+x*(a-bx*2)/(a+bx*2)2]≠2,4. (12) (13) 其中, a11=1+τ*[-3x*2+2(m+1)x*-m-x*(a-bx*2)/(a+bx*2)2],a12=-τ*x*/(a+bx*2), a13=2τ*[-3x*+m+1+bx*2(3a-bx*2)/(a+bx*2)3],a14=τ*(bx*2-a)/(a+bx*2)2, a15=-6x*+2(m+1)+2bx*2(3a-bx*2)/(a+bx*2)3,a16=-x*/(a+bx*2), a17=6τ*[-1+(a2bx*+b3x*5-6ab2x*3)/(a+bx*2)4],a18=2τ*bx*(3a-bx*2)/(a+bx*2)3, a19=-6x*+2(m+1)+2bx*2(3a-bx*2)/(a+bx*2)3,a110=(bx*2-a)/(a+bx*2)2, a21=cτ*,a22=1-cτ*,a23=-2cτ*/x*,a24=-2cτ*/x*, a25=2cτ*/x*,a26=c,a27=-c,a28=6cτ*/x*2,a29=-4cτ*/x*2, a210=2cτ*/x*2,a211=-2c/x*,a212=-2c/x*,a213=2c/x*. (14) 对映射(13)做如下可逆变换 (15) 则映射(13)转化为 (16) 其中, 利用中心流形定理[14],讨论映射(16)在不动点(0,0,0)处存在的中心流形WC(0,0,0),利用下式近似表示 经计算,可以得到 考虑映射(16)限制在中心流形上WC(0,0,0)的部分,得到1个一维映射: (17) 其中, μ2=[a15(λ2-a11)-a12a26]/(1+λ2)-(1+a11)[a16(λ2-a11)-a12a27]/[a12(1+λ2))], a12a211]+2(1+a11)(λ2-a11)(a24e2-a110)+2e2(λ2-2a11-1)[a14(λ2-a11)-a12a25]+ (1+a11)(2a27e2+2a12a213)-a212(1+a11)2}+a16(λ2-a11)[e1(λ2-a11)-e2(1+a11)]/[a12(1+λ2)], μ4=e2[a15(λ2-a11)-a12a26]/(1+λ2)+e2(λ2-a11)[a16(λ2-a11)-a12a27]/[a12(1+λ2)], 若要一维映射(17)发生倍周期分岔,需要以下2个判定量不为零,即 (18) 根据Neimark-Sacker分岔定理[16]对时空离散捕食系统的Neimark-Sacker分岔进行分析.Neimark-Sacker分岔发生的第1个条件要求式(8)中的2个特征值是1对模为1的共轭复数,即p2-4q<0且q=1.换言之, τ2[c-3x*2+2(m+1)x*-m-x*(a-bx*2)/(a+bx*2)2]-(4cτ2x*)/(a+bx*2)<0, (19) (20) 当参数条件满足式(19)、(20)时,通过平移变换w=x-x*,z=y-y*将不动点(x*,y*)移至原点,利用泰勒展式将映射(6)转化为以下映射 (21) 其中,系数a11,a12,a13,a14,a17,a18,a21,a22,a23,a24,a25,a28,a29,a210均在式(14)中给出,需替换τ*为τ0.因此,映射(21)在不动点(0,0)处雅可比矩阵的2个特征值也是模为1的共轭复数,可以表示为 (22) (23) (λ(τ0))θ≠1,θ=1,2,3,4. (24) 由于在Neimark-Sacker分岔的第1个条件(19)中已满足p(τ0) ≠-2,2,因此条件(24)等价于p(τ0)≠0,1,即 τ0[c+3x*2-2(m+1)x*+m+x*(a-bx*2)/(a+bx*2)2]≠2,3. (25) 对映射(21)应用如下可逆变换 (26) 则映射(21)转化为 (27) 其中, 为了使映射(27)在(0,0)附近发生Neimark-Sacker分岔,需要满足判定量 (28) 其中, (29) 将式(29)代入条件(28),得到 (30) 其中, 综上可知,如果同时满足条件(19)、(20)、(23)、(25)、(30),则离散捕食系统在不动点(x*,y*)处发生Neimark-Sacker分岔.当a0<0且d>0时,在τ>τ0处分岔出吸引的不变环[10];当a0>0且d>0时,在τ<τ0处分岔出排斥的不变环. (31) (32) 其中,f1=x+τf(x,y),g1=y+τg(x,y).在不动点(x*,y*)处进行泰勒级数展开,得到 (33) (34) (35) 方程(35)的傅里叶通解为 (36) (37) 令 (38) 则方程(37)的雅可比矩阵为 (39) 根据文献[10,17],当雅可比矩阵(39)的1个特征值大于1时,时空离散捕食系统发生图灵分岔.因此图灵分岔发生的必要条件为 |a11k1+a22k2|>(1+k1k2detJ*). (40) 经上述分析计算可知图灵分岔的发生分为以下2种情况: 1)当满足以下不等式时,扩散驱动的加1分岔发生 |a11k1+a22k2|<(1+detJ*). (41) detJ*<1. (42) 1-(a11k1+a22k2)+k1k2detJ*<0. (43) 2)当满足式(41)、(42),且1+(a11k1+a22k2)+k1k2detJ*<0时,扩散驱动的减1分岔发生. 根据2.1节的计算结果,通过数值模拟展现时空离散捕食系统中由倍周期分岔和Neimark-Sacker分岔引发混沌路径上的各类吸引子和斑图转变. 根据文献[11],可行的参数范围为0 图1 倍周期分岔图(a)、(c)以及相对应的最大李雅普诺夫指数图(b)、(d)Fig.1 Diagrams of flip bifurcation (a)、(c) and corresponding maximum Lyapunov exponents plot (b)、(d) 为研究倍周期分岔引发混沌路径上的复杂动力学行为,选取τ=1.25,1.42,1.46和1.58模拟混沌路径上的周期和混沌吸引子,以及在这些吸引子发生图灵失稳所产生的复杂斑图(d1=0.01,d2=0.50,δ=5).结果表明:随τ的增大吸引子变化,呈现了离散系统在周期振荡态和混沌振荡态之间的转变.并且随着τ增大时空离散捕食系统斑图的无序度也增大,捕食系统的斑块性也逐渐走向破碎. 借助斑图空间振幅[18]变化和时空发展动态演变[19-21]分析混沌路径上斑图转变的规律,虽然时空离散捕食系统斑图的斑块空间分布规律并不明显,但斑图空间振幅变化表明映射(6)的周期吸引子能够投射到空间上,振幅变化体现出周期或扭转周期动态.对应于倍周期分岔引发混沌路径上的周期加倍级联过程,斑图振幅的变化周期也呈现出类似的加倍过程,解释了斑图中斑块破碎性的增强现象.当系统进入混沌区域时,斑图振幅的变化呈现出更复杂的动态. 斑图的时空发展变化[22-23]则进一步清晰地展示时空离散捕食系统从周期到混沌的转变过程.结果表明,当斑图对应的吸引子为周期时,斑图的时空发展呈现稳定的冻结边界,并且该模式不随时间改变,此时系统处于冻结混沌状态;当对应的吸引子为混沌时,时空发展的冻结边界被打破,出现一些自由点,此时系统呈现缺陷湍流的状态. 在数值模拟中,固定参数值m=0.02,a=1.6,b=2.8,c=0.1,计算得到发生Neimark-Sacker分岔的临界值为τ0=2.209 214,此时判别量d=0.018 526,a0= -0.098 570,说明在τ>τ0处分岔出吸引的不变环.图2a展示了映射(6)随着参数τ变化的Neimark-Sacker分岔图,当τ<τ0时,系统的不动点(x*,y*)是稳定的;当τ>τ0时,发生Neimark-Sacker失稳.图2b展示了Neimark-Sacker分岔图所对应的最大李雅普诺夫指数,从图中可以看出,Neimark-Sacker失稳会导致系统在τ=3.588附近首次进入混沌.根据图2b中展现的最大李雅普诺夫指数的波动特征来看,系统在进入混沌区后仍会回到周期轨道.图2c和图2d用局部放大图展示了系统在混沌区的周期窗口. 图2 Neimark-Sacker分岔图(a)、(c)以及相对应的最大李雅普诺夫指数图(b)、(d)Fig.2 Diagrams of Neimark-Sacker bifurcation (a)、(c) and corresponding Maximum Lyapunov exponents plot (b)、(d) 为研究Neimark-Sacker分岔引发混沌路径上的复杂动力学行为,选取τ=2.6,4.25,4.5和4.7模拟混沌路径上的不变环、周期和混沌吸引子,以及在这些吸引子发生图灵失稳所产生的复杂斑图(参数取值d1=0.01,d2=0.5,δ=20).结果表明,随τ的增大系统经历了周期、拟周期和混沌等不同吸引子;此外发现时空离散捕食系统在混沌路径上的斑图类型以环状和螺旋波状为主,且随着捕食系统向混沌区域深入,空间斑图螺旋波呈现更强的不规则性变化. 斑图的空间振幅变化和时空发展动态演变则解释了混沌路径上的螺旋波斑图转变规律.对应于拟周期和周期吸引子,斑图的空间振幅变化呈现出集束状的区块结构,在每一个区块中体现了拟周期和周期的振荡变化,对应的时空发展也呈现出规则的带状结构;对应于混沌吸引子,斑图的空间振幅变化无序且混乱,难以发现规律性,但此时的时空发展变化揭示出在混沌状态下离散系统整体上仍旧具有某种有序的时空带状自组织结构.对比两种情形,系统在混沌时的时空带状结构是有缺陷的,每一条带上状态变化维持稳定的时间呈现混乱的分布,说明此时系统处于某种整体有序但是局部混乱的湍流状态. 本文研究的时空离散Leslie-Gower型捕食系统共有3个不动点,其中仅有1个不动点反映捕食者和被捕食者可稳定共存.在此稳定不动点做扰动,捕食系统可发生倍周期分岔、Neimark-Sacker分岔和图灵分岔.倍周期分岔图、Neimark-Sacker分岔图以及相对应的最大李雅普诺夫指数图证实了这2种分岔都开启了通往混沌的路径,结合图灵分岔发现系统在混沌路径上可引发混沌斑图自组织转变.当发生倍周期分岔时,在通往混沌路径上的周期加倍级联过程会映射到斑图振幅的变化,斑图也呈现类似加倍过程,且随着控制参数的增大,斑图的斑块性逐渐走向破碎.在周期吸引子对应的斑图上,其时空发展变化呈现出稳定的冻结边界,系统处于冻结混沌状态;混沌吸引子对应斑图的时空发展的冻结边界被打破,开始出现一些自由点,此时系统为缺陷湍流状态.当系统发生Neimark-Sacker分岔时,斑图自组织以环状和螺旋波状为主,随着控制参数的增大,空间斑图螺旋波的不规则性增强.在拟周期和周期吸引子所对应的斑图上,斑图的空间振幅变化呈现集束状的区块结构,且每个区块也呈现出拟周期和周期的振荡变化,对应的时空发展变化呈现出规则的带状结构;在混沌吸引子所对应的斑图上,其空间振幅变化无序且混乱,但对应的时空发展变化在整体上仍旧具有某种有序的时空带状自组织结构,说明系统处于某种整体有序但是局部混乱的湍流状态.2 分岔分析
2.1 倍周期分岔
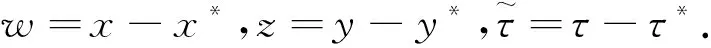
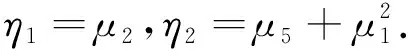
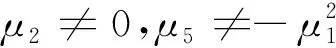
2.2 Neimark-Sacker分岔
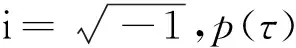
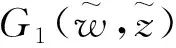
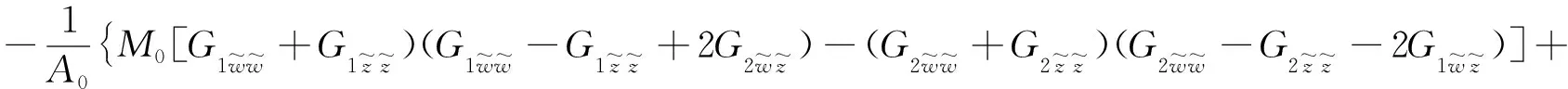
2.3 图灵分岔
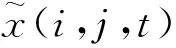
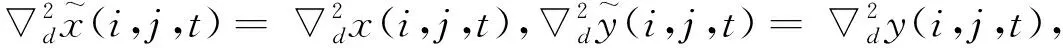
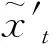
3 混沌路径上的斑图转变
3.1 倍周期分岔引发混沌路径上的斑图转变
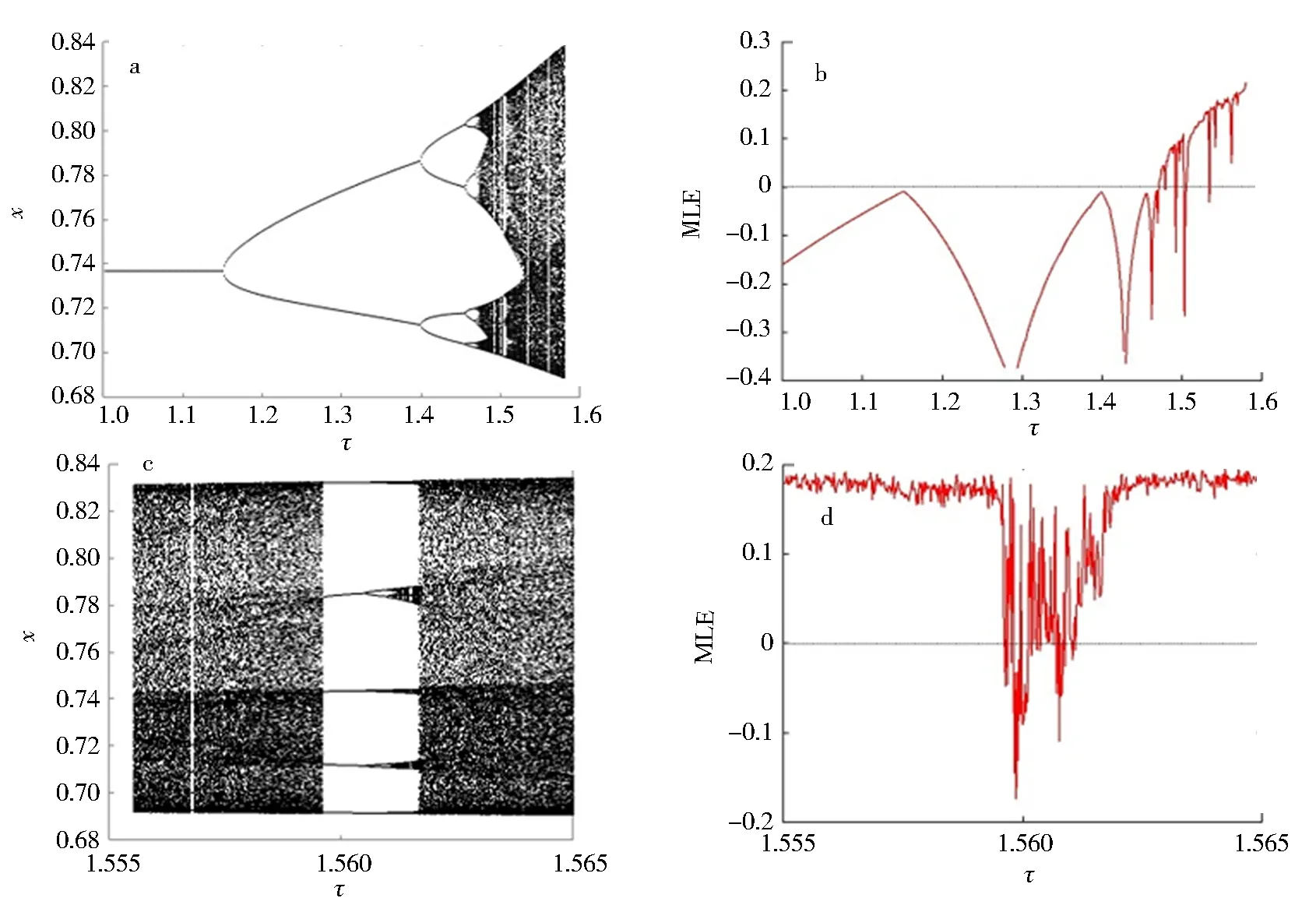
3.2 Neimark-Sacker分岔引发混沌路径上的斑图转变
4 结论

