基于图像块鲁棒抑制式模糊C均值图像分割

郑一博,李忠灿,程杨鑫,董雨荷,朱占龙

(河北地质大学 信息工程学院,河北省光电信息与地球探测技术重点实验室,河北 石家庄 050031)

无损检测技术是利用声、光、电等手段,对零件瑕疵、目标物等感兴趣目标,进行大小、位置、数量等信息的检测,主要方法有超声、涡流、红外检测等[1].由于成像受到电磁干扰、遮挡物、噪声干扰等不利环境影响,易导致图像出现模糊不清、边缘浑浊等问题,使得对感兴趣目标进行分割与检测造成困难.一般情况下,无损检测图像分割为目标区和背景区,其中目标在图像上往往只占据较小面积,故两区域面积相差较大,灰度分布呈现不均衡特性[2],因此,探索适应性强、鲁棒性好的分割算法具有理论意义和现实需要.

模糊C均值算法(FCM)是一种有效的图像分割算法,为了提升分割效率,抑制式模糊C均值算法(SFCM)被提出[3],其本质在于提升高隶属度、惩罚低隶属度,缺点是需人为由经验设定参数α控制抑制程度.文献[4]提出了该参数的自适应确定方法,提升了算法的自适应性.考虑到灰度(样本)分布不均衡特性导致的较小类聚类中心向较大类“移动”问题,类的总隶属度[5-6]、类的数量[7]等表征类大小的指标被融入聚类进程而减缓这种“移动”趋势,但上述方法仍存在鲁棒性较差的缺点,所以自适应引入邻域信息构建符合灰度分布不均衡特性图像的目标函数值得进一步研究.

图像块[8-9]广泛地应用于图像去噪领域,利用图像块代替其中心像素显然有更强的鲁棒性.在迭代过程中,每个图像块的类别属性也是不尽相同的.本文以图像块为基本单位,构建图像块的模糊不确定性来衡量图像块的类别属性,考虑类的总隶属度指标构建新的目标函数,以期形成具有较强鲁棒性和自适应性,能有效分割灰度分布不均衡特性图像的算法,其中涉及图像块内各像素权重和抑制参数自适应确定问题.最后,采用无损检测图像对所提出的算法进行测试.

1 抑制式模糊C均值算法

(1)

其中,U={uij}为c×N矩阵,V={vi}为c×1矩阵.

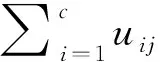
(2)

(3)

FCM算法迭代步骤如下：

S1：初始化聚类中心vi;

REPEAT

S2：由式(2)计算隶属度uij;

S3：由式(3)更新聚类中心vi;

UNTIL(聚类中心稳定)

提出抑制式模糊C均值算法[3]的初衷是奖励高隶属度、惩罚低隶属度从而提高聚类速度.从迭代过程上来说,相比FCM,改变之处是在步骤S2和S3之间添加新的步骤进行隶属度调整,如下：

以第j个像素点xj为例进行说明.假如uij>usj(s≠i;s=1,…,c),则相应的隶属度调整为

uij=1-α∑s≠iusj,

(4)

其中,α∈[0,1]为惩罚因子,决定了对隶属度的惩罚力度.SFCM算法的执行步骤如下：

S1：初始化聚类中心vi;

REPEAT

S2：由式(2)计算隶属度uij;

S2*：由式(4)调整隶属度uij;

S3：由式(3)更新聚类中心vi;

UNTIL(聚类中心稳定)

可见,相比FCM,SFCM算法添加了调整隶属度的步骤S2*.

2 本文算法

2.1 图像块各像素权重

设Nj表示以像素xj为中心像素的图像块,q为图像块大小(图像块为q*q),gjr表示Nj内像素的灰度值,其中r为图像块内像素的索引.值得注意的是,gj5(q=3)表示Nj的中心像素灰度值.令wjr为Nj中各像素权重,表达式如下：

wjr=ws·wp,

(5)

其中,ws表示Nj内中心像素与邻域像素之间的空间位置关系,wp表示各像素的灰度关系.ws表达式为

ws=1/(1+djr),

(6)

其中,djr表示Nj中像素xj与邻域像素xr的空间欧式关系.显然地,距离中心像素位置越近的邻域像素,所得到的权重越大,反之,权重越小.

wp的计算过程采用了自适应的手段,计算过程如式(7)～(10)所示.

首先判断图像块Nj内像素灰度值为噪声(边缘)的可能性,判断方法为

(7)

需指出,σj表示所在图像块内像素的标准差.按照文献[10]推荐的系数,式中限定l=1.如果βjr为1,则该像素被判定为噪声(边缘),则舍弃该像素参与赋权的计算.对Nj中剩余像素变化情况进行衡量,如下：

(8)

(9)

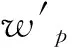
wjr=ws·wp/∑r∈Nj(ws·wp).

(10)

2.2 基于图像块模糊不确定性的聚类模型

图像块模糊不确定性是指在每一次迭代过程中,当聚类中心确定后,图像块属于某个类别的不确定性.更具体地,一个图像块距离所属类别的聚类中心越近且距离其他聚类中心越远则视为该图像块具有更强的类别属性,在目标函数中所起的作用应该越小[12],这里把图像块Nj的模糊不确定性建模为

(11)

由式(11)可知,在第i次的迭代中聚类中心确定时,aj的值为定值.聚类结果应该使得模糊不确定性最小,则

(12)

可见,参数的引入,可以提升类别不明显的图像块对目标函数的作用,这样,可以提升不同类之间的可分性.

2.3 本文算法的目标函数及求解

将图像块及其模糊不确定性模型引入模糊C均值算法,同时考虑灰度分布不均衡特性,构建目标函数：

(13)

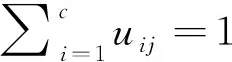
(14)

(15)

由式(14)可以看出,隶属度表达式为嵌套的表达式,这里在编程时需要预先给定(初始化)隶属度或者由式(2)得到初始的隶属度,本文中利用式(2)得到了初始的隶属度,具体见表1.

表1 SFCMP算法执行步骤

前面提到SFCM算法迭代过程中引入了参数α,需要根据经验手动设置,自适应性较差,文献[4]给出一种有效的自适应设定方法,有

(16)

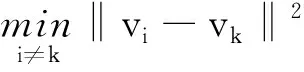
2.4 本文算法的执行流程

本文算法执行步骤如表1所示.

3 实验结果

为验证本文SFCMP算法的有效性和鲁棒性,采用无损检测图像进行实验,同时以SFCM算法[3]、MSFCM算法[4]、ISFCM算法[5]、文献[6]算法和WIPFCM算法[8]作对比,实验环境为Matlab (R2014a)、2.10 GHz AMD®CoreTMA8-5550 M处理器,4 GB内存,Windows7旗舰版操作系统.另外,对SFCMP算法和对比算法的参数进行设定,如表2所示.

表2 算法参数设定

实验用的无损检测图像及相应的标准分割图如图1所示,其中图1a-c是原始图像,图1d-f是标准分割图,图1g-i是灰度分布图.可见,此3幅图灰度分布不均衡,满足测试需求.

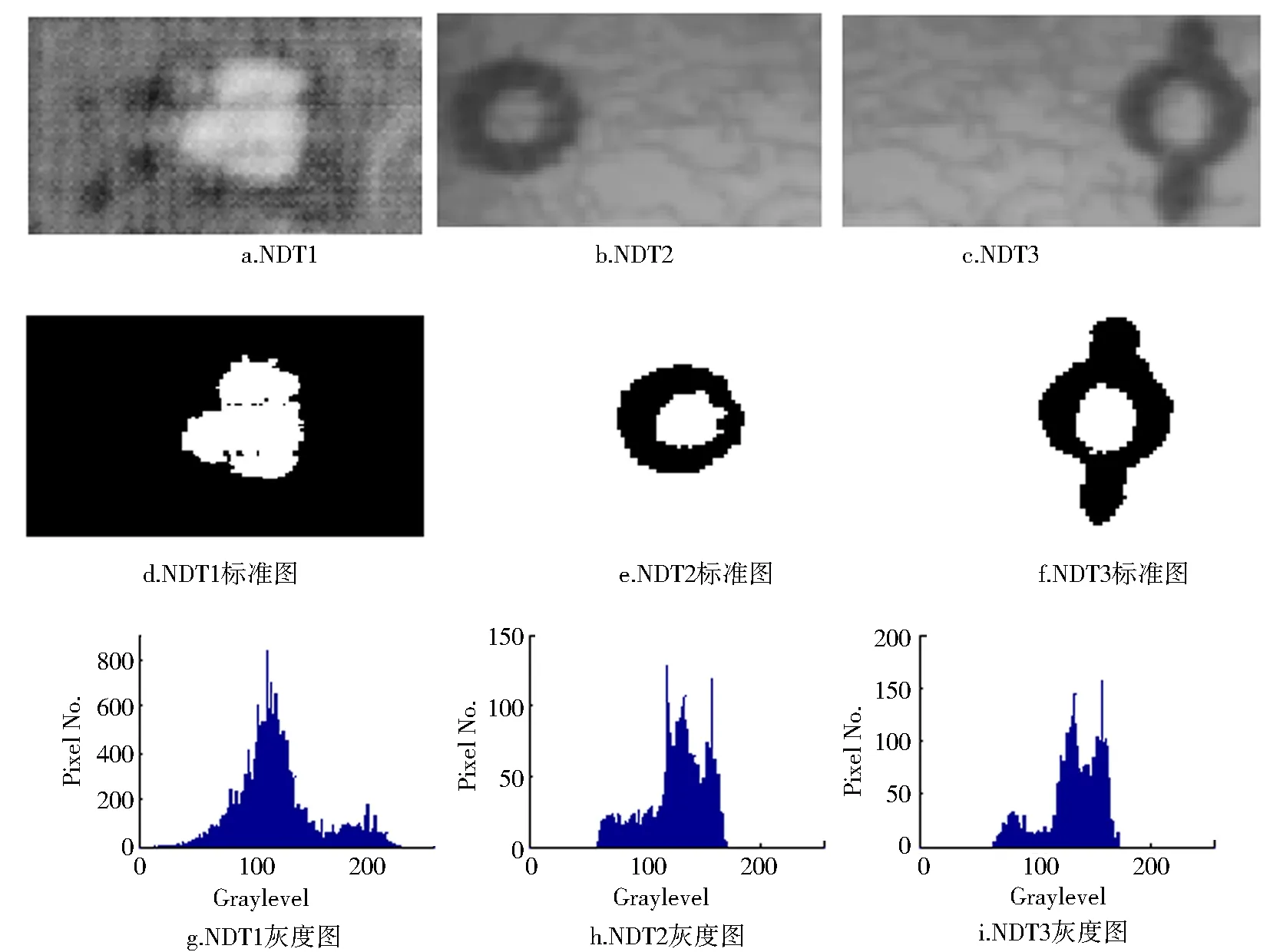
图1 实验用无损检测图像Fig.1 NDT images for test

为测试算法鲁棒性,对图像添加高斯噪声(Gaussian noise, GN)或椒盐噪声(salt &pepper noise,SPN).不失一般性,对NDT1-NDT3均添加GN(0,0.02)的高斯噪声或SPN(0.1)的椒盐噪声,然后采用表2中算法进行分割实验,结果如图2、3所示.

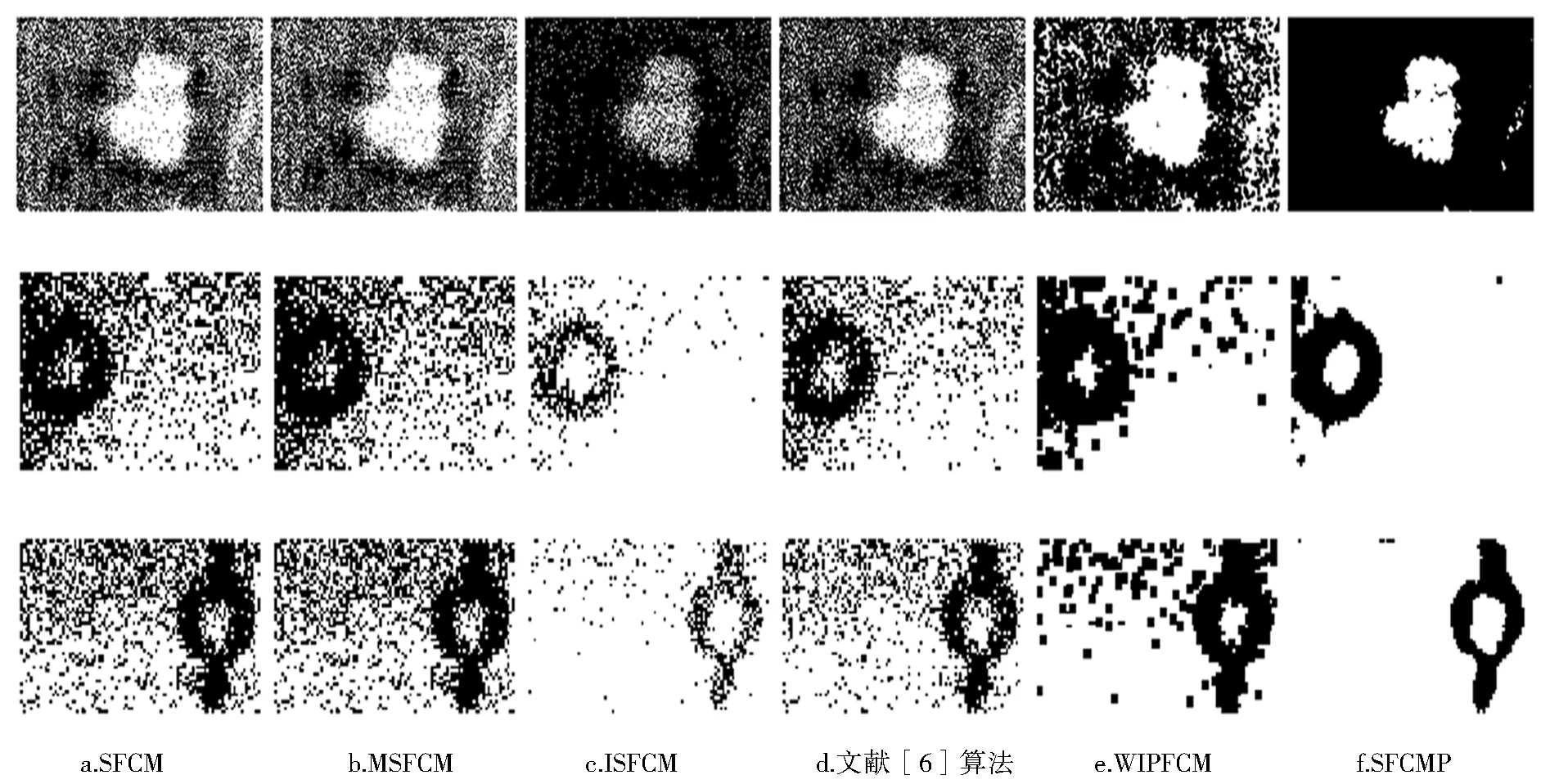
图2 对NDT1-NDT3添加GN(0,0.02)噪声后的结果Fig.2 Segmentation results of NDT1-NDT3 with GN(0,0.02) noise

将图2、图3所示的分割结果与图1中相应的无损检测图像的标准分割图相比,可以看出,在噪声干扰下,SFCMP算法可以更有效分割具有灰度分布不均衡特征的图像,最为直观的表现是本文算法得到的分割结果背景和目标更为清晰,显示了算法的鲁棒性和自适应性.需要指出的是,文献[6]算法在SPN(0.1)的干扰下能够有效分割NDT2、NDT3图像,但是在分割结果中目标不够平滑清晰,受到了噪声的影响,其他算法均不能有效地分割具有灰度分布不均衡的图像,且分割结果明显受到了噪声的影响.

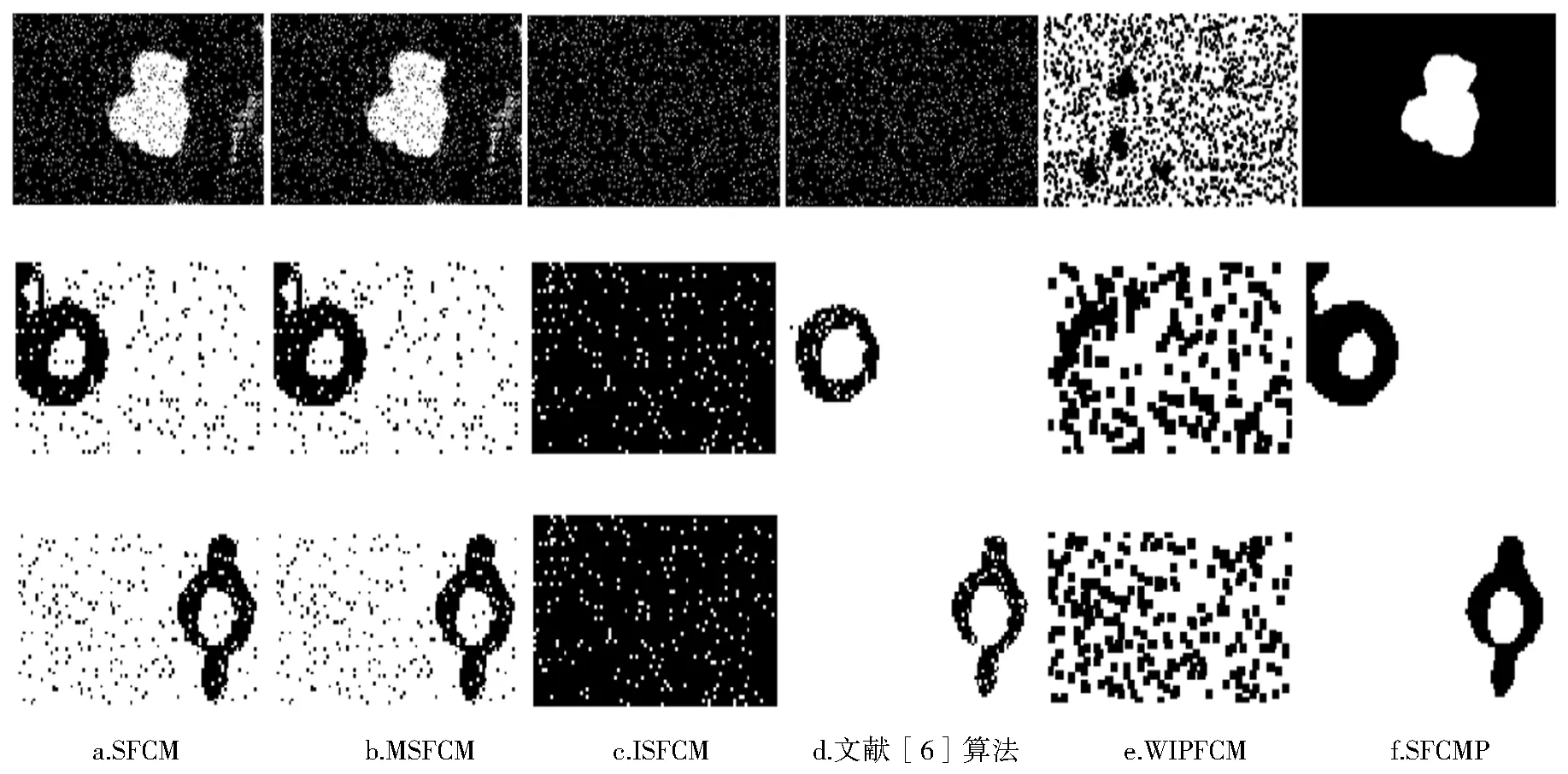
图3 对NDT1-NDT3添加SPN(0.1)噪声后的结果Fig.3 Segmentation results of NDT1-NDT3 with SPN(0.1) noise

4 结论

在考虑类的总隶属度前提下,利用图像块来代替单个像素进入模糊C均值的迭代进程,其中图像块各像素权重受邻域像素与中心像素的空间关系影响,也受图像块各像素的灰度关系影响,在文中给出了权重的自适应确定过程.在迭代过程中,构建了图像块模糊不确定性模型,提升了类别特征不明显图像块的影响力,最后利用NDT图像进行实验,结果显示出SFCMP算法的鲁棒性和有效性.