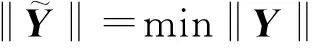四元数广义Sylvester方程M自共轭混合结构解

徐云,黄敬频

(广西民族大学 数学与物理学院,广西 南宁 530006)

随着四元数被广泛应用到工程、量子力学、计算机科学、信号和彩色图像处理等领域[1-6],许多重要矩阵方程的研究也从复数域扩展到四元数体.Sylvester方程就是一类具有广泛实际应用背景的方程,在特征结构配置、微分方程数值解、航天控制、模式识别等领域都有着广泛的应用.目前关于Sylvester方程以及它的各种推广形式的求解方法,已经有丰富的研究成果[7-14].文献[8]讨论了混合Sylvester矩阵方程组相容的充要条件,给出了该方程组的通解表达式及其解的极大极小秩;文献[11]通过矩阵对的广义奇异值分解(GSVD)及标准相关分解(CCD)给出了混合Sylvester矩阵方程的最小二乘解;文献[12]利用四元数矩阵的实分解和箭形矩阵的特征结构讨论了Sylvester方程的箭形矩阵解及其最佳逼近问题;文献[13]利用四元数矩阵的实分解和矩阵的Kronecker积研究了四元数Sylvester方程具有Toeplitz矩阵约束解存在的条件及其最佳逼近问题;文献[14]给出了广义Sylvester方程的广义反自反解.然而在四元数体上针对广义Sylvester矩阵方程AX-YB=C的某些混合结构解的研究目前未见相关的研究报导,对此本文提出并讨论该方程的一类M自共轭混合结构解.

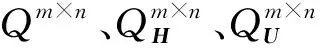
定义1[16]给定四元数矩阵M∈Qn×m,若矩阵X∈Qn×n满足(M*XM)*=M*XM,则称X为M自共轭矩阵.显然当M=I时,X即为自共轭矩阵,因此自共轭矩阵是特殊的M自共轭矩阵类.

定义2[17-18]设A∈Qm×n则称LA=I-A+A,RA=I-AA+,分别为四元数矩阵A的左、右诱导算子.根据Moore-Penrose广义逆的定义,易知ALA=LAA+=0,A+RA=RAA=0,LA*=RA,RA*=LA.

性质1[19]设A、C∈Qn×n,则下列等式成立：

1)LA=(LA)2=(LA)*,RA=(RA)2=(RA)*;

2)LA(CLA)+=(CLA)+,(RAC)+RA=(RAC)+.

本文具体研究下列2个问题：

问题1已知A,B,C∈Qm×n,M∈Qn×m,寻找M自共轭矩阵X和自共轭矩阵Y满足

AX-YB=C,

(1)

这时矩阵对(X,Y)称为广义Sylvester方程(1)的M自共轭混合结构解.

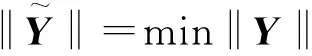
(2)

1 问题1的解

首先,对给定的四元数矩阵M∈Qn×m,设rank(M)=r,并对M作奇异值分解(SVD),

(3)

引理1[16]给定四元数矩阵M∈Qn×m,并设rank(M)=r,则X∈Qn×n是M自共轭的充分必要条件为

(4)

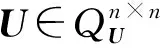
注1 根据引理1可知,当X2=0,X3=0时,矩阵(4)仍为M自共轭矩阵.记

(5)

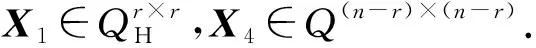
寻找问题1的混合结构解(XM,Y).若形似式(5)的矩阵XM及自共轭矩阵Y是方程(1)的混合结构解,则将式(5)带入方程(1)可得

(6)

记

AU=[A1,A2],BU=[B1,B2],CU=[C1,C2],

(7)

其中,A1,B1,C1∈Qm×r,A2,B2,C2∈Qm×(n-r).于是式(6)等价于方程组

(8)

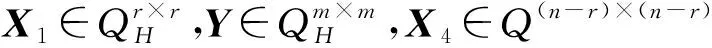
引理2[19]设A∈Qm×p,B∈Qq×n,C∈Qm×s,D∈Qt×n,E∈Qm×n,且P1=RAC,Q1=DLB,S1=CLP1,则方程AX1B+CX2D=E有解的充要条件是

RP1RAE=0,RAELD=0,ELBLQ1=0,RCELB=0,

有解时其通解为

其中,U1、U2、U3、V1、V2为任意适当阶数的矩阵.

对于方程组(8)给出的四元数矩阵A1,A2,B1,B2,C1,C1,

(9)

定理1设四元数矩阵A,B,C∈Qm×n,M∈Qn×n,rank(M)=r,M的奇异值分解为式(3),则问题(1)存在混合结构解,当且仅当

(10)

有解时,其通解表达式为

(11)

其中,U由式(3)给出,且

(12)

其中,Ai,Bi(i=1,2,…,5),C1,C2,C3,P,Q,S,N1,N2如式(7)和式(9)所示,W1,T1,T2,T3,T4,T5,Z为任意适当阶数的矩阵.

证明：对于方程组(8)的第1个方程

A1X1-YB1=C1,

(13)

存在自共轭解(X1,Y)的充要条件是方程组

(14)

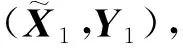
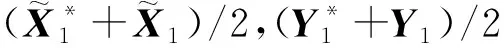
RA1C1LB1=0

(15)

有解时,其解的表达式为

(16)

其中,W1,W2,W3为任意适当阶数的矩阵.将式(16)带入式(14)的第2个方程,并由式(9)中的A3,B3有

(17)

由式(9)中的A4,B4,A5,B5,C3及式(17)两边分别左乘RA3和右乘LB3得

A4W2B4+A5W3B5=C3,

(18)

再由引理2,方程(18)关于W2,W3是相容的,当且仅当

RPRA4C3=0,RA4C3LB5=0,C3LB4LQ=0,RA5C3LB4=0,

(19)

式(18)有解时,其通解表达式为

(20)

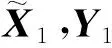
(21)

为方程(14)的自共轭解.最后把Y的表达式代入方程组(8)的第2个方程,并结合引理2可得

(22)

其中,Z为任意适当阶数的矩阵.于是问题1的混合结构解(XM,Y)由式(11)～(12)给出.证毕.

当方程(1)中矩阵B=0时,问题1就简化为求方程

AX=C

(23)

的酉相似块对角M自共轭解.于是根据定理1可得如下推论.

推论1设A,C∈Qm×n,则矩阵方程(23)存在酉相似块对角M自共轭解的充要条件为

(24)

其中,Ai,Ci(i=1,2)由分解式(7)给出.方程(23)有解时,其通解表达式为

(25)

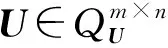
(26)

J1为任意自共轭矩阵,J2为任意矩阵.

当方程(1)中矩阵A=0时,问题1就简化为求方程

YB=-C

(27)

的自共轭解.于是根据定理1可得如下推论.

推论2设B,C∈Qm×n,则矩阵方程(27)存在自共轭解的充要条件为

CLB=0,B*CB+=C*BB+,

(28)

方程(27)有解时,其通解的表达式为

(29)

其中,

Y1=-CB+-(B*)+C*RB+RBK1RB,

(30)

K1为任意适当阶数的矩阵.

2 问题2的解

设A,B∈Qm×n,rank(A)=p,rank(B)=q,且

s=rank(A)+rank(B)-rank([A,B]),l=rank([A,B])+rank(B*A)-rank(A)-rank(B),

则矩阵对(A,B)的CCD-Q分解具有如下形式[21]：

(31)

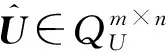
(32)

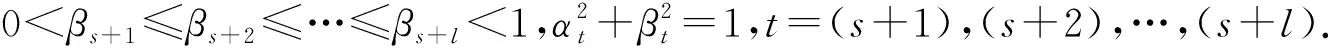
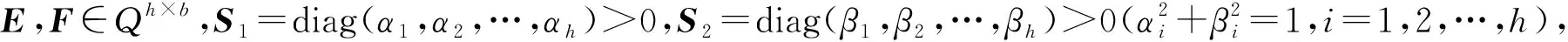
minf=‖S1X-E‖2+‖S2X-F‖2.

(33)

证明：记E=[eij]h×b,F=[fij]h×b,X=[xij]h×b,那么

显然f是关于hb个四元数变量xij的连续可微函数,因此根据多元函数的极值理论容易得到

minf⟺xij=αieij+βifij,i=1,2,…,h,j=1,2,…,b⟺X=S1E+S2F.

证毕.

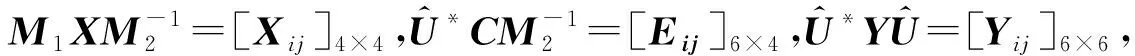
(34)

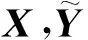
(35)

(36)

其中,

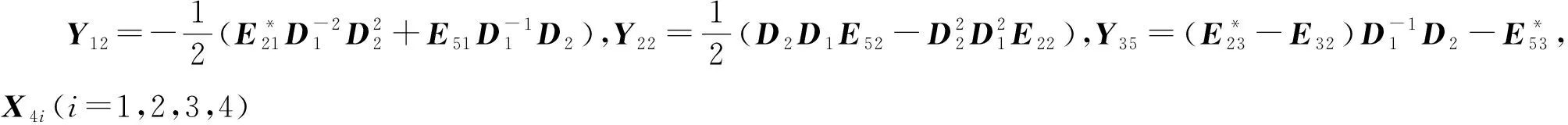
证明：由矩阵对(A,B)的CCD-Q分解式(31),可将方程(1)等价写成

(37)

则

(38)

等价于

(39)

(40)

由式(39)、(40)可得

(41)

由式(39)、(41)可得

(42)

(43)

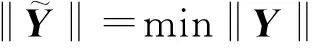
Y11=0,Y44=0,Y45=0,Y55=0,Yj6=0(j=1,2,…,6),

(44)

且

(45)

应用引理3求解最小化问题(45),可得

(46)

将式(44)、 (46)代入式 (42) 、(43),可得式(35) 、(36),证毕.

3 数值算例

给出四元数矩阵A,B,C∈Q4×4,M∈Q4×4如下：

试判断广义Sylvester方程(1)的M自共轭混合结构解(XM,Y)的存在性.若存在,求出其一组解.

首先,对矩阵M作奇异值分解(SVD)：M=Udiag(G,0)V*,其中,

其次,根据方程组(8)可得

其中,

通过计算可得：

RA1C1LB1=0,RPRA4C3=0,RA4C3LB5=0,

C3LB4LQ=0,RA5C3LB4=0,RA2C2LB2=0.

因此,根据定理1可知,所给广义Sylvester方程存在混合结构解(XM,Y),并由式(11)所确定.下面根据式(11)、(12),取U1,V1,V2,V3,V4,V5,R为零矩阵,可得一组M自共轭混合结构解

其中,

4 结论