函数零点问题的求解路径分析

江苏省溧阳中学 韩 俊

众所周知,极限与导数(微积分)紧密相关,很多导数问题与极限思想都息息相关.苏教版教材在高中数学课程中不涉及极限的知识,这给很多涉及导数的函数问题的求解带来了重重困难.例如,含参的函数零点讨论问题,这是近些年来函数压轴的常见题型,笔者就借此题型来分享几个含参函数零点问题的解题感悟.

1 引例

1.1 分析

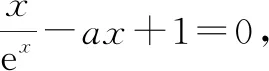
①

数形结合,如图1我们发现:

图1

再细想,一来学生对函数图象的趋势(极限思想)不一定能准确把握,二来作为解答题,这样的解答似乎略显苍白,因此,需要用文字和数学表达式来准确证明上面的结论,即用零点存在定理来证明零点的存在性.那么,如何取点就变成了学生解决此题的难点.许多学生“为题消得人憔悴”,但依旧不得.重新审视此题,笔者略谈一二,希望能够给此类题型提供一些解题思路.

1.2 解析

再考虑非特值:

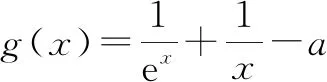
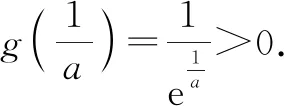
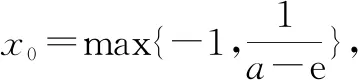
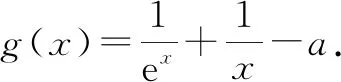
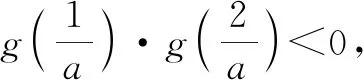
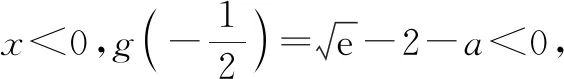
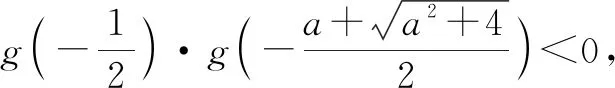
1.3 总结

从上述解题过程看,找到使得函数值异号的点大致可以选择以下三种路径.

路径一:把代数式中已经能判定符号的式子取出,再将剩余部分视作“零”,通过解方程找到所需定号的“点”.

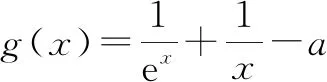
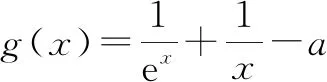
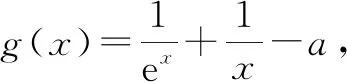
2 三种路径在压轴题中应用

经过上题的研究,笔者有些“众里寻他千百度,蓦然回首,那人却在,灯火阑珊处”之感.下面利用这三种路径来解决如下高考压轴题.

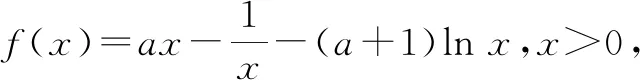
当a≤0时,ax-1≤0.所以,当x∈(0,1)时,f′(x)>0,f(x)单调递增;当x∈(1,+∞)时,f′(x)<0,f(x)单调递减.故f(x)max=f(1)=a-1<0,此时函数f(x)无零点,不合题意.

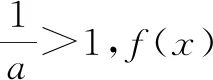
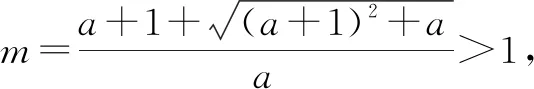
综上,a 的取值范围为(0,＋∞)．

评析：通过该题的解析不难发现,在讨论当0＜a＜1时,可先利用路径二由x＞1得到,再利用路径三由ex≥x＋1的变形式elnx≥lnx＋1得到lnx≤x－1,进而得到lnx＜x,用x替换x,得lnx＜2 x,则f(x)＞ax－1－2(a＋1)x ＝,则存在使得f(m)＞0．

3 结束语

通过上文两题所述,大多数的函数“找点”问题都可从上述三种路径中摸索出一些解题思路,虽不一定能“众里寻他千百度,蓦然回首,那人却在,灯火阑珊处”,但也希望通过此文为一些“为题消得人憔悴”的朋友们,在解决此类问题时点亮一丝“灯火”．

正如波利亚所说：“如果你有一个念头,你就够幸运的了;如果你走运的话,你或许能找到另一个念头;真正糟糕的事是,我们根本就没有念头,1001ba1001ba,这时任何一个可能指明问题新方向的问题,都值得欢颂,因为它可以引起我们的兴趣,可以使我们继续工作,继续思索．”所以,解题永无止境,收获永无止境,愿看过此文的朋友在解决压轴题时,总能经历三境,不断升华．