例析求函数解析式的方法与技巧

山东省乐陵第一中学 张 伟

“求函数解析式” 是《普通高中教科书·数学·必修一》(人教版)的重要内容,是进一步学习“基本初等函数”和“函数的应用”的基础.在高考中,通常不会直接考查函数的解析式,但解析式往往是解函数题的基础,所以学习和掌握求函数解析式的方法与技巧非常重要.在具体解题中,可以尝试运用以下六种方法.

1 配凑法

配凑法是一种结构化的方法,即根据已知函数的类型及解析式的特征,配凑出复合变量的形式,从而求出解析式.具体方法是:由已知条件f[g(x)]=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),即可得到f(x)的表达式.使用配凑法时,要注意定义域的变化.

配凑法的关键在于如何“配”和“凑”,让题目的条件转化为容易求解的形式,方法灵活多样,不同的题目,配凑的方法不同.

例1已知f(x+1)=x2-3x+2,求函数f(x)的解析式.

解：因为f(x+1)=x2-3x+2=(x+1)2-5(x+1)+6,所以f(x)=x2-5x+6.

方法与技巧：配凑法的技巧大多是配凑公式,例如本题中就是化用了公式(a-b)2=a2-2ab+b2,只需把原复合函数解析式配凑成关于x+1的多项式即可.

2 换元法

换元法即变量替换,其实质就是转化.通过转化达到“化繁为简、化难为易、化陌生为熟悉”的目的.对于形如y=f[g(x)]的函数解析式,令t=g(x),从中求出x=φ(t),然后代入表达式求出f(t),最后将t换成x,得到f(x)的解析式.换元时要注意新元的取值范围.

例3已知af(4x-3)+bf(3-4x)=2x,a2≠b2,求函数f(x)的解析式.

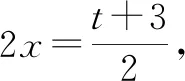
①

将①中的t换成-t,得

②

①×a-②×b,得

由a2≠b2,得a2-b2≠0.

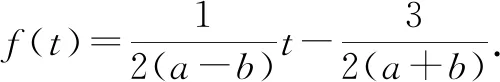
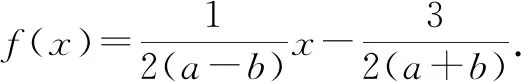
方法与技巧：因为本题的左边有多项式4x-3,所以首先将4x-3换为t,然后再将t换成-t,求出f(t)后再将t换成x,最后得到f(x)的解析式.

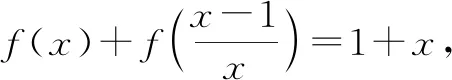
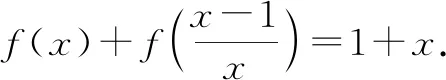
③

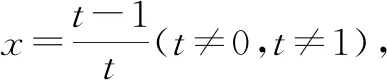
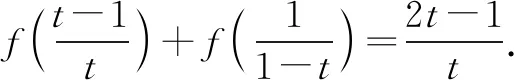
④

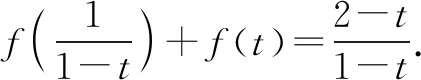
⑤

由③式,可得

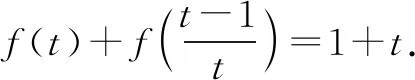
⑥

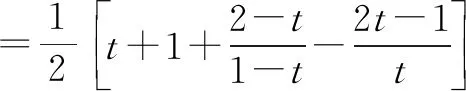
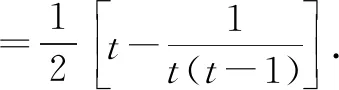
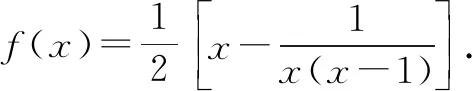
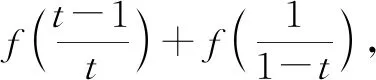
3 待定系数法

如果已知所求函数的类型(如一次函数、二次函数),可先设出所求函数的解析式,再根据题意列出方程组求出系数.具体方法是:先设出含有待定系数的解析式,再利用恒等式的性质,或将已知条件代入,建立方程(组),通过解方程(组)求出相应的待定系数.

例5已知f(x)是二次函数,且f(0)=0,f(x+1)=f(x)+x+1,求函数f(x)的解析式.

解：设f(x)=ax2+bx+c(a≠0).由f(0)=0可知c=0,所以f(x)=ax2+bx.

又f(x+1)=f(x)+x+1,所以

a(x+1)2+b(x+1)=ax2+bx+x+1.

即ax2+(2a+b)x+a+b=ax2+(b+1)x+1.

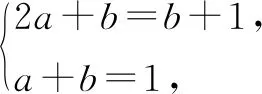
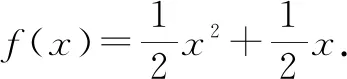
方法与技巧：由已知条件可知f(x)是二次函数,所以设f(x)=ax2+bx+c(a≠0).由于推知c=0,于是得出ax2+(2a+b)x+a+b=ax2+(b+1)x+1,进而根据对应系数相等的关系,求出a,b的值即可.

例6若二次函数f(x)的顶点坐标为(1,4),其与x轴的交点为(-1,0),试求函数f(x)的解析式.

解法1：设函数f(x)=ax2+bx+c(a≠0),则有

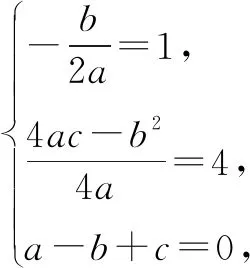
所以f(x)=-x2+2x+3.

解法2：设f(x)=a(x+m)2+k,因为当m=-1时,k=4,所以f(x)=a(x-1)2+4.

由f(-1)=0 ,得a(-1-1)2+4=0,则a=-1.

故f(x)=-x2+2x+3.

方法与技巧：本题的两种解法都运用了待定系数法.解法1运用二次函数的一般式f(x)=ax2+bx+c(a≠0),通过解方程组求出a,b,c的值代入获解;解法2运用二次函数的顶点式f(x)=a(x+m)2+k来求解.它们有异曲同工之妙.

4 解方程组法

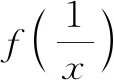
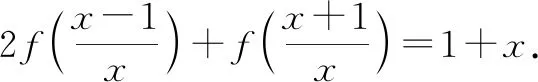
⑦

⑦式中用-x代替x,得

⑧

联立⑦⑧,解得

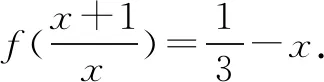
⑨

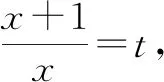
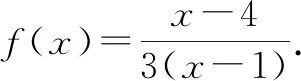
方法与技巧：本题根据题设条件用-x代替x,构造一个对称方程组,通过解方程组即可得到f(x)的解析式.

例8已知函数f(x)满足f(-x)+2f(x)=2x,求f(x)的解析式.

解：将f(-x)+2f(x)=2x中的-x用x代换,得f(x)+2f(-x)=2-x.

联立两式,解得3f(x)=2x+1-2-x.

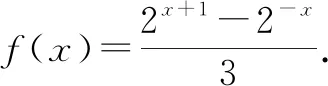
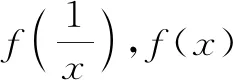
5 赋值法

赋值法的解题思路是对变量取适当的特殊值,使问题具体化、简单化,进而依据结构特点找出一般规律,求出函数解析式.

例9已知f(0)=1,f(a-b)=f(a)-b(2a-b+1),求函数f(x)的解析式.

解：令a=0,得

f(-b)=f(0)-b(1-b)=b2-b+1.

令-b=x,得f(x)=x2+x+1.

方法与技巧：从本题可以看出赋值法的解题规律.①当所给函数方程含有两个变量时,可以考虑对这两个变量交替用特殊值代入,或使这两个变量相等代入,再运用已知条件,即可求出函数解析式;②根据题目的具体特征来确定取什么特殊值;③取特殊值代入的目的,是为了使问题具体化、简单化,进而找出规律,求出函数解析式.

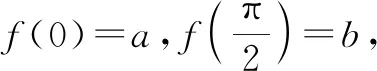
解：令x=0,y=t,得

f(t)+f(-t)=2acost.

⑩

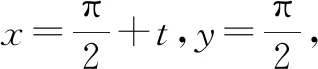
f(π+t)+f(t)=0.

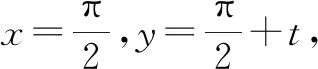
f(π+t)+f(-t)=-2bsint.

所以f(x)=acosx+bsinx.

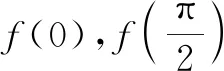
6 代入法

代入法求函数解析式的特点是,知道已知函数图象或者方程曲线的一个点A,通过题目中的关系,用所求的函数图象或者方程曲线上点B的坐标表示出点A的坐标,再将点A的坐标代入已知的函数或者方程中,即可求出所需的函数解析式或曲线方程.

例11已知定义在实数集R上的函数y=f(x)图象关于直线x=2对称,并且在[0,2]上的解析式为y=2x-1,求函数f(x)在[2,4]上的解析式.

解：设M(x,y)x∈[2,4]在函数f(x)的图象上,点M′(x′,y′)与M关于直线x=2对称,则

又y′=2x′-1.

所以y=2(4-x)-1,即y=7-2x.

故函数f(x)在[2,4]上的解析式为y=7-2x.

方法与技巧：从本题的求解过程可以看出,求已知函数关于某点或者某条直线的对称函数时,采用代入法比较简捷.

例12如图1,某地有一座形如抛物线的石拱桥,已知其跨度为37.4 m,拱高为7.2 m,求此石拱桥所在抛物线的解析式.

图1

解：如图2,以抛物线的对称轴为y轴,以宽AB的中点为原点,建立平面直角坐标系xOy,令抛物线的解析式为y=ax2+7.2.

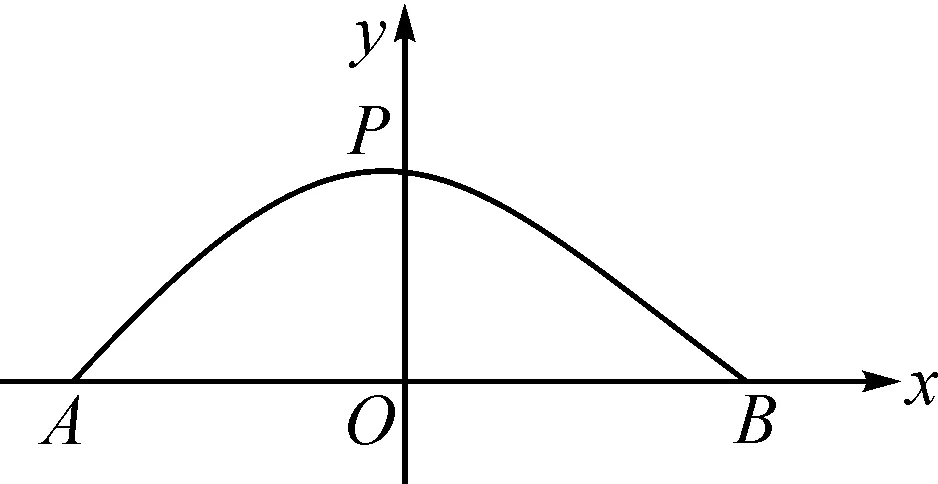
图2

将点B(18.7,0)代入,得0=(18.7)2a+7.2.

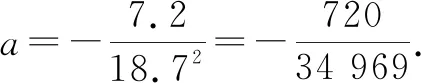
方法与技巧：本题属于抛物线的实际应用题,体现了数形结合的思想,解题技巧在于把抛物线放在合适的平面直角坐标系中,设出相应的解析式,这样能够使解题过程变得简洁.

通过对上述典例的解析,我们可以看到,娴熟地运用“六法”可以应对绝大多数求函数解析式类的题型,“六法”各自既有其独特性,相互之间又有联系,有时一种题型可以用几种方法来求解,达到一题多解的效果.