AH60C 高强钢热变形下动态再结晶行为研究

赵兴通 闫 寒 田海涛 陈丛虎 霍桂兰

（安阳钢铁股份有限公司）

0 前言

高强度钢广泛应用于工业领域，在社会经济中具有举足轻重的地位。安阳钢铁近几年开发了强度大于460 MPa 的AH60C 微合金化高强钢，AH60C高强钢强度高、抗震性强，市场需求量较大[1]。因此，本研究主要针对AH60C 微合金化高强钢热变形下的动态再结晶行为进行研究，微合金钢在热变形条件下的动态再结晶可以降低位错密度、影响变形抗力、细化晶粒等，从而进一步提高产品的力学性能[2-3]。该研究通过Gleeble-3800 热模拟机对AH60C 高强钢进行单道次压缩试验，研究了AH60C 高强钢在变形温度850 ℃、950 ℃、1 050 ℃，应变速率0.1 s-1、1 s-1、10 s-1条件下的动态再结晶行为，计算出AH60C 高强钢α、n、A等材料参数以及热变形激活能Q，建立本构方程，利用加工硬化原理确定动态再结晶临界条件，得到了临界条件和热变形参数之间的定量关系，从而为AH60C高强钢在实际中的热加工工艺制定、优化以及生产提供一定的参考依据。

1 试验材料和方法

该试验材料为安钢生产的AH60C 高强度结构钢连铸坯，工艺流程：转炉→吹氩站→LF 精炼炉→VD →宽板坯连铸机，化学成分见表1。

表1 AH60C 化学成分

在200 mm×1 500 mm 连铸坯上取200 mm×750 mm 的试验样，将试验样切割并加工成φ8 mm×12 mm 的圆柱体，打磨成光滑表面。在设定的变形温度、应变速率、应变量等条件下，利用Gleeble-3800 热模拟机进行恒温、恒应变速率的压缩试验。采用单道次压缩试验，将试样以20 ℃/s 加热至1 200 ℃，保温5 min，然后以10 ℃/s 冷却至850 ℃、950 ℃、1 050 ℃，保温10 s 开始变形，应变速率为0.1 s-1、1 s-1、10 s-1，应变量为1.20，快速水冷，试验方案参数见表2，工艺如图1 所示。

表2 AH60C 单道次压缩试验方案

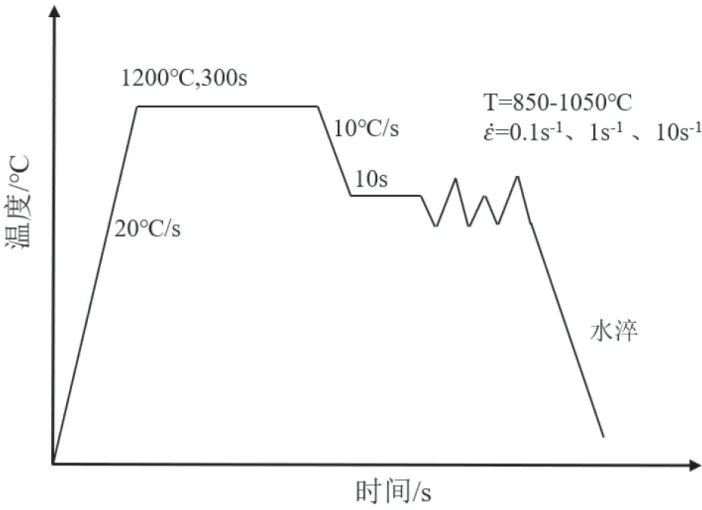
图1 单道次压缩试验工艺

2 结果与讨论

2.1 不同变形条件下应力-应变曲线

AH60C 高强钢在不同变形温度和不同应变速率下的应力应变曲线，如图2 所示。

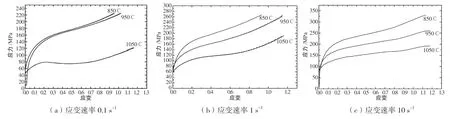
图2 AH60C 应力应变曲线

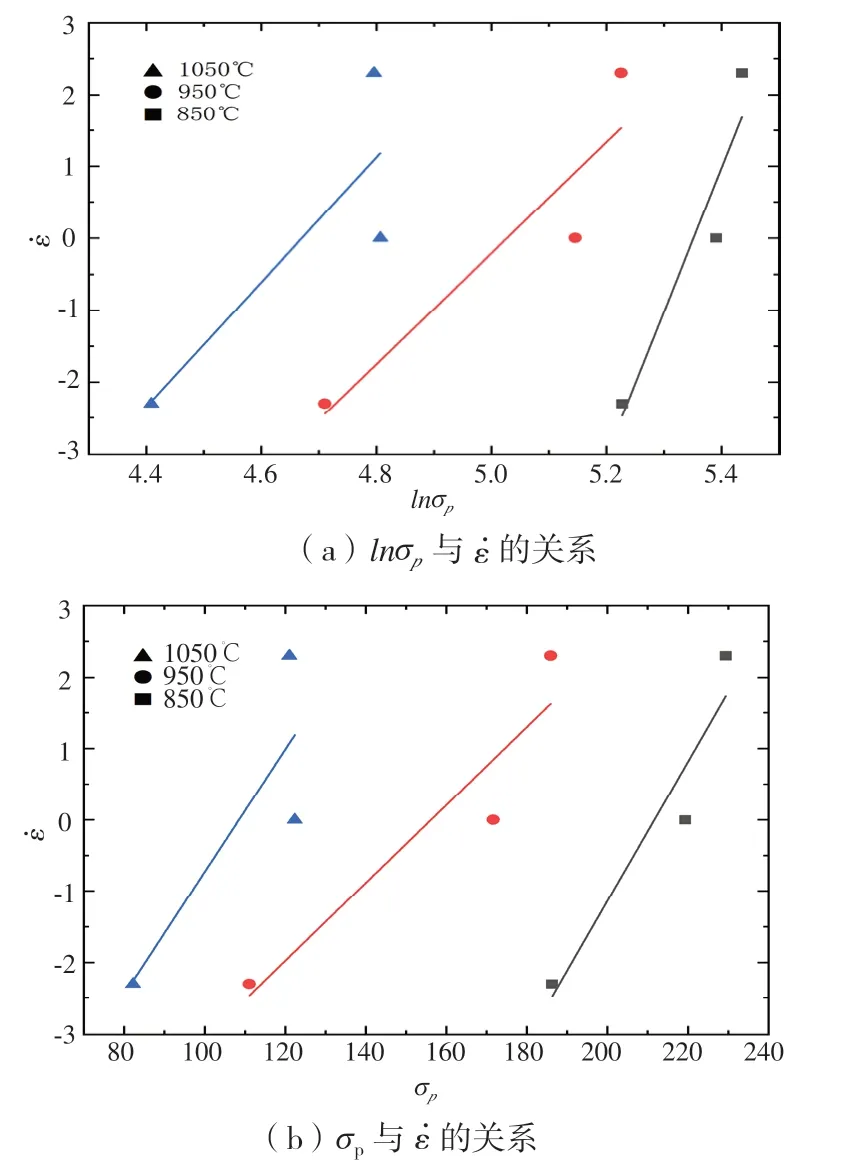
图3 峰值应力与应变速率的关系

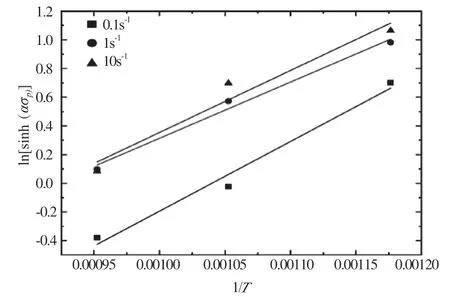
图4 与ln[sinh（ασp)]的关系

从图2 可以看出，应变速率一定时，随着变形温度的升高，流变应力降低。并且，流变应力随着应变的增大而迅速增大，明显呈现出加工硬化现象。随着变形温度的升高，分子间的动能增加，导致原子间的结合力逐渐降低，此时合金的变形抗力随着变形温度的升高逐渐降低。当应变速率为0.1 s-1，变形温度达到1 050 ℃时，变形抗力先增加后下降，明显发生了动态再结晶行为。当变形温度在950 ℃、850 ℃时，随着应变的增加，流变应力不断增加，并没有显示出动态再结晶现象。在热变形激活能的控制下，动态再结晶的形核率随着变形温度的不断升高而不断增大，从而增加了晶核长大的驱动力，进而增强了动态再结晶的软化作用。因此，随着变形温度的升高，流变应力逐渐降低，动态再结晶的程度逐渐增加。相反，随着变形温度的降低，流变应力逐渐增加，动态再结晶的程度逐渐降低，甚至不会发生动态再结晶现象。当应变速率为1 s-1时，变形温度达到1 050 ℃时，应力应变曲线有减缓趋势，说明有发生动态回复，可以判断出该应变速率下的软化作用弱于应变速率为0.1 s-1时。随着应变速率的增大，应力应变曲线没有出现很好的峰值现象，是因为随着应变速率的增大，在变形过程中很快形成了足够的位错塞积，变形储能就会很快超过临界值，从而诱发动态再结晶。这一过程快速、反复进行，晶粒尺寸较小，对后续变形阻力减小程度不明显，很难出现动态再结晶特征曲线的完美峰值，甚至不会出现动态再结晶现象。此外，所需的时间会随着应变速率的提高而缩短，导致应变更加局部化，此时需要更大的应力才能使整体材料都发生应变，因此随着应变速率的增大，流变应力不断增大。

2.2 变形激活能

从以上试验得到的应力-应变曲线分析，已知随着变形温度的降低，峰值应力以及对应的能量越高，动态再结晶发生的可能性越小。这种关系可以通过Zener-Hollomon（Z）来表示[4]：

Z是温度补偿变形因子。当变形温度较低，并且变形程度较高时，Z值越大。

与高温金属材料变形过程不同的是，高温延伸过程类似的热激活能过程取决于变形温度和变形速率，因此可以选用包含变形激活能Q和温度T的双曲正弦方程描述[5-7]。

低应力水平下：

高应力水平下：

可以通过A、α、n、Q之间的关系来描述高温的流变特性。

热变形的条件已被W.J.M.Tegart 和C.M.Sellars通过实验验证了，可用温度补偿电压率的齐纳-霍尔参数来表示[8]：

对式（2）、式（3）、式（4）两边取对数，计算得到以式（5）、式（6）、式（7）：

通过单道次压缩试验得到的AH60C 在不同温度不同速率条件下的峰值应力σp，见表3。

表3 AH60C 高强钢峰值应力

利用方程线性回归法，取得三条线上的平均斜率，得n'=10.186 15，β=0.079 323，故α==0.007 787（mm2/N）。

对于所有应力下，T和σ之间可以用双曲线正弦关系表示：

由以上可知，α=0.007 787 mm2/N，化学成分对n 值的影响较大，不同的化学成分对n 值的影响不同，因此需要通过实验来确定n 值。对式（8）两边取对数，得：

同理，通过式（9）可以看出ln[sinh（ασp)]与ln之间也存在线性关系，n 为斜率。因此得到其二者之间的关系曲线（如图5 所示），推断出平均值n=8.116 563。

图5 ln[sinh（ασp)]与ln的关系

由此可以算出AH60C 高强钢动态再结晶激活能Q=Rnb=293 305.163 J/mol。

通过式（1）和式（4）可以得出：

通过不同温度下的应变速率得到不同的Z值，从而得到不同的Z 值与A[sinh（ασ）]n其中对应的峰值应力的对应关系（见表4），根据式（7）绘制出lnZ与ln[sinh（ασ）]的曲线关系（如图6 所示），通过线性回归方程所得的直线得出lnA=26.701 52。

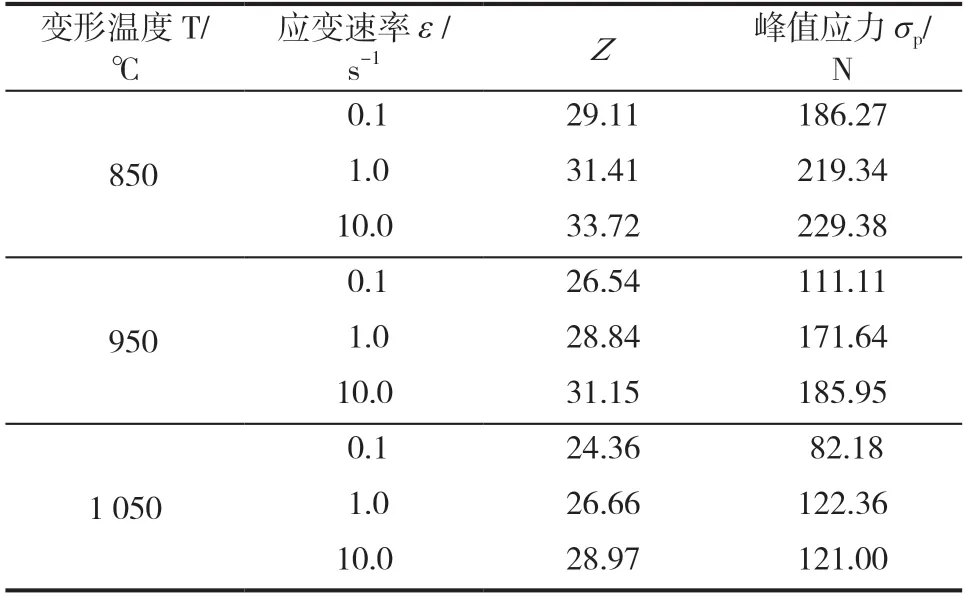
表4 Z 值对应峰值应力σp

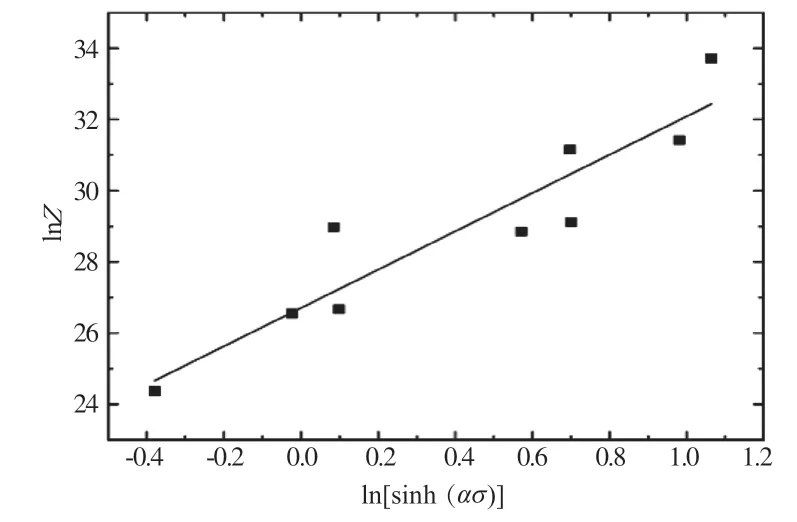
图6 lnZ 与ln[sinh（ασ）]的关系

因此计算得到AH60C 高强钢峰值应力条件下的高温本构方程：

2.3 动态再结晶临界条件

如前所述，所得到的的应力应变曲线并没有明显的显示出动态再结晶的特性峰值，但也不能说明该过程仅仅发生了动态回复，并没有发生动态再结晶。其中，动态再结晶临界条件是关键的研究目标，因此利用Poliak 和Jonas 研究发现的θ-σ关系曲线，当材料发生动态再结晶时，θ-σ关系曲线会出现拐点，即∂2θ/∂σ=0。对其求导推导出∂（lnθ）/∂ε=∂θ/∂σ，说明不仅θ-σ曲线会出现拐点，lnθ-ε曲线也会出现拐点。因此，通过应力应变曲线绘制lnθ-ε曲线，利用∂2（lnθ）/∂ε=0 计算出临界应变，进而确定动态再结晶发生的临界条件[9]。当变形温度在1 050 ℃，应变速率0.1 s-1条件下，应力应变曲线如图7所示。

图7 变形温度1 050 ℃、应变速率0.1 s-1 时的应力应变曲线

该试验获得的应力应变曲线无法直接从曲线中计算出加工硬化率θ，通过对曲线进行拟合得到拟合方程，在经过微分得到在应变下的加工硬化率θ，绘制出lnθ与ε曲线以及∂（lnθ）/∂ε与ε曲线，如图8 所示。

图8 变形温度1050℃、应变速率0.1s-1 时的ε 及∂（lnθ）/∂ε 与ε 之间的关系

从图8 可以看出，在应变0.1 附近出现拐点，对其曲线进行三次拟合，得到：

当∂2（lnθ）/∂ε=0 时，所对应的应变即为材料在1 050 ℃、应变0.1 s-1时对应的临界应变εc=0.134 27。

因此，通过此方法绘制出该高强钢在不同条件下的lnθ与ε曲线，如图9 所示。

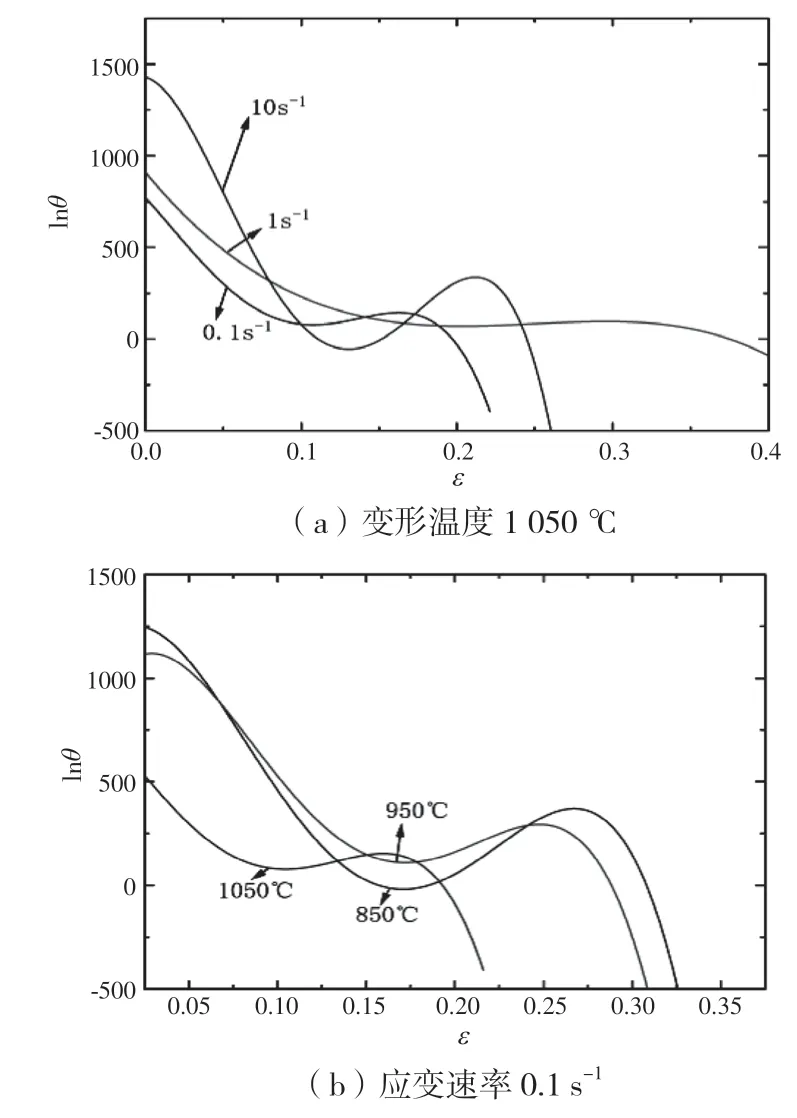
图9 AH60C 不同变形温度和不同应变速率下的lnθ 与ε 关系曲线

从图9 可以看出，不同变形温度、不同应变速率下lnθ-ε曲线不同。加工硬化率在变形初期迅速降低，随着变形增大逐渐进入缓慢阶段，在缓慢阶段出现了拐点。

不同变形温度和不同应变速率下的∂（lnθ）/∂ε与ε的关系如图10 所示。

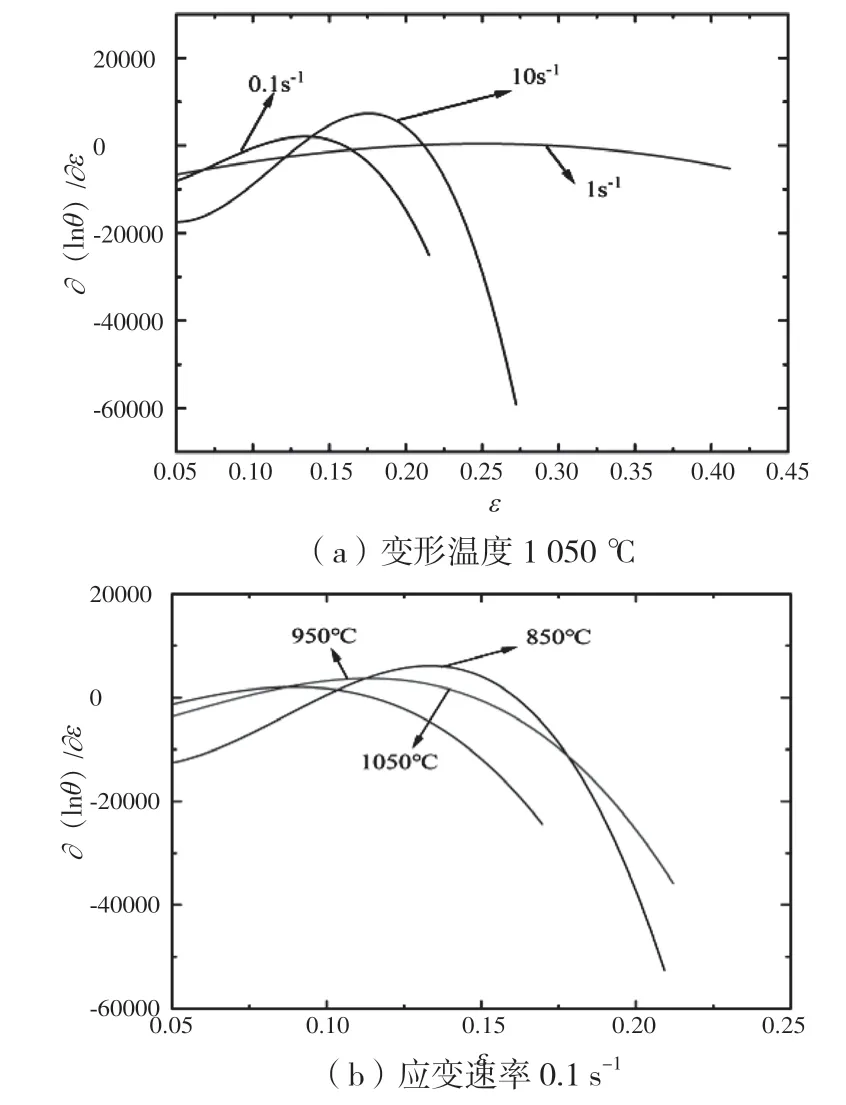
图10 AH60C 不同变形温度和不同应变速率下的∂（lnθ）/∂ε 与ε的关系

从图10可以看出，∂（lnθ）/∂ε-ε均有最大值，且最大值时的应变对应着lnθ-ε 曲线拐点处应变，此处应变为AH60C 高强钢发生动态再结晶时的临时应变。当变形温度一定时，临界应变随着应变速率的增大而增大；当应变速率一定时，临界应变随着变形温度的增大而减小。

使用最广泛的Sellras 模型来表示临界应变：

对其两边求对数，得：

根据不同变形温度和不同应变速率下的临界应变εC和对应的Z值，绘制出lnεC-lnZ散点图，对其进行线性拟合，如图11 所示。

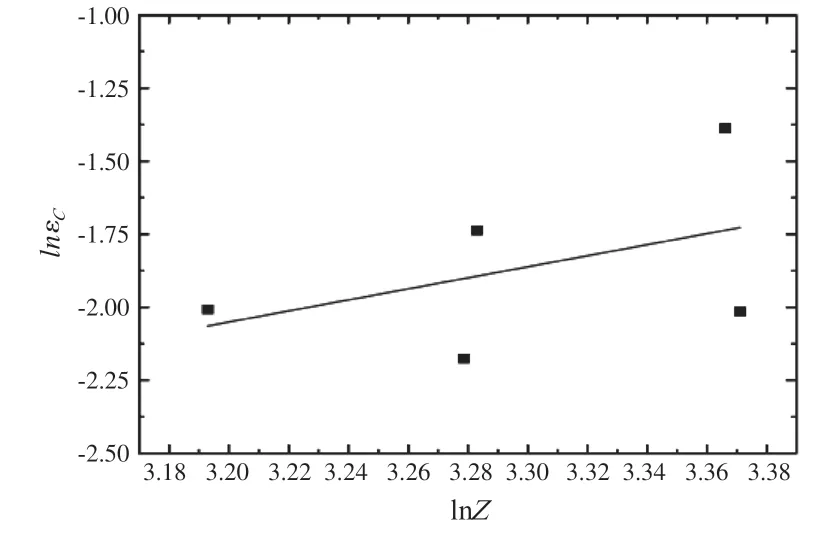
图11 lnεC-lnZ 之间的关系

由图11 可得到拟合方程：

故，临界临界应变预测模型为

3 结论

（1）AH60C 高强钢在不同变形条件下对动态再结晶行为有显著的影响，随着变形温度的升高，流变应力降低；随着应变速率的增大，流变应力增大，并且变形温度越高，应变速率越低，动态再结晶越彻底；采用Zener-Hollomon 参数的正弦函数计算出材料参数值α、n、A 以及AH60C 高强钢热变形激活能Q为293 305.163 J/mol。

（2）AH60C 高强钢应力应变曲线具有动态再结晶特征，其变形温度达到1 050 ℃，应变速率达到0.1 s-1时应力应变明显出现了完全动态再结晶现象；并且lnθ-ε 曲线出现拐点，在∂（lnθ）/∂ε与ε曲线出现最大值，曲线最大值对应的应变即为动态再结晶临界应变。

（3）AH60C 高强钢发生动态再结晶行为时，临界应变随着变形温度的升高而降低，随着应变速率的增大而增大，且在本次试验条件下，AH60C 高强钢以及动态再结晶临界应变预测模型为εC=3.04×10-4Z1.88975。