一种带终端视线角约束的反舰导弹三维协同制导律
张书森,孟秀云,丁 晓
(北京理工大学宇航学院,北京 100081)
0 引言
现代战争态势不断发展,反导系统愈加完善,仅靠单枚导弹难以满足作战需要,多枚导弹协同攻击能够有效弥补单枚导弹突防能力不足、抗干扰能力差的缺陷,因此,多枚导弹协同攻击更符合现代化信息作战的需要[1]。
最早的多导弹协同攻击策略是通过给各枚导弹设置相同的攻击时间实现的,导弹个体之间互不干扰、独立作战,归根结底研究的还是单枚导弹的制导问题[2],严格意义上讲不属于真正的协同,真正的协同无需在导弹发射前预置飞行时间,而是通过导弹在飞行过程中不断的信息交互进而达到攻击时间一致[3],为了实现对目标的全方位打击,在多导弹时间协同的基础上,还要求导弹以期望的角度攻击目标,将导弹- 目标相对运动方程建立在视线坐标系下是一种较为常用的方法[4-6],沿视线方向设计制导律可以协调导弹飞行的时间,沿视线法向设计制导律可以使导弹以特定的视线角攻击目标。
现有的制导律大多基于二维平面内导弹- 目标相对运动模型设计的,针对三维空间设计制导律的文献较少,本文针对多枚导弹同时攻击海面上机动的舰船这一场景,设计一种有终端视线角约束的三维协同制导律,在视线方向上,区别于文献[4-6]采用构造关于时间的滑模面的方式,本文采用多智能体一致性理论设计时间协同制导律,制导算法相对简洁;在视线法向上,本文设计一种带终端视线角约束的非奇异自适应滑模制导律,精度高且收敛速度快,最后选取特定场景对所设计的制导律进行仿真验证。
1 导弹目标三维相对运动模型
本文将导弹- 目标相对运动方程建立在视线坐标系下,如图1 所示,MXLYLZL为视线坐标系,OXIYIZI为惯性坐标系,qθ、qφ分别为视线倾角和视线偏角。

图1 三维空间弹目相对运动几何关系图Fig.1 Geometric relation diagram of relative motion between missile and target in three-dimensional space
相对速度在视线坐标系下的表达如下:
式中,VR为弹目接近速度,ω 为视线坐标系相对大地坐标系的旋转角速度,R 为弹目相对距离。
在视线坐标系下有:
根据视线坐标系与大地坐标系的转换关系有:
将式(2)、式(3)代入式(1)可得:
根据牛顿第二定律有:
将式(3)、式(4)代入式(5)可得三维空间下导弹-目标相对运动动力学方程组形式如下:
其中,aM=[aMxaMyaMz]T为导弹在视线坐标系下三轴方向的加速度,aT=[aTxaTyaTz]T为目标在视线坐标系下三轴方向的加速度,本文的目的在于通过设计沿视线方向上的加速度aMx,使得多枚导弹同时击中目标;通过设计沿视线法向上的加速度aMy、aMz,一方面使得视线角速率在导弹接近目标的过程中快速趋近于零,另一方面控制导弹在末端以期望的视线角攻击目标。
2 三维协同制导律设计
2.1 视线方向上制导律设计
定理1[7]:如果存在一个含有n 个节点的系统可以用G=(V,E,A)描述,并且节点的状态可以用一阶动态环节表达,那么对于任意给定的初值ξi(0),∀i∊V,当t→∞时,有ξi=ξj,∀i,j∊V,则称系统节点之间的状态能够达到渐进一致。
式中,ξi∊Rm用于描述第i 个节点的状态;ui∊Rm用于描述第i 个节点的输入。
一种常见的一致性算法表达形式如下:
假设节点间的通信拓扑结构保持固定,采用式(8)的控制算法,使得系统状态能够达到渐进一致的必要条件是G 中存在有向生成树,系统最终的一致状态由状态初值、通信拓扑结构和加权矩阵共同决定[8]。特别地,如果G 是无向图,那么系统状态将会达到平均一致,一致状态为:
为方便起见,令导弹同时启动发射的时刻为时间原点,记为t=0 时刻,在此后的飞行过程中,记Ri为t 时刻第i 枚导弹与目标的相对距离,vi为t 时刻第i 枚导弹与目标的接近速度,Ri、vi均是关于时间t的函数。
对Ri关于时间t 求导有:
式中,Ri的值可以根据导弹和目标的位置坐标求出,vi的值可以分别将导弹和目标的速度投影到视线坐标系下得到。
根据求得的Ri和vi,即可估计出第i 枚导弹击中目标的时刻为:
式中,i=Ri/vi为第i 枚导弹在当前时刻下的期望攻击时间(expected time-of-attack,ETA)。
根据式(10),显然有:
由式(11)可以看出,多枚导弹同时击中目标即击中时刻一致,等价于在某一时刻t 之后各导弹的期望攻击时间一致。
将式(10)两边同时对时间t 求导,并将式(9)代入可得:
将式(9)两边同时对时间t 求导:
将式(13)与式(6)第1 式代入式(12)可得:
令ui=α(i-v)ii/vi,将对aMx的控制转化为对ui的控制,显然有
式(16)满足定理1,ζi为状态变量,因此,上述所设计的算法能够使各枚导弹的击中时刻达到渐进一致,即实现多导弹协同攻击。
由于ζi与i等价,选取i作为状态变量,参照式(8)、式(15)可以得到一种简洁的分布式控制算法:
根据式(17),通过设计导弹之间的通讯拓扑结构和加权邻接矩阵,即可计算出各枚导弹的速度指令,从而得到所需要的视线方向加速度指令,进而实现多枚导弹期望攻击时间一致。
2.2 视线法向上制导律设计
在进行视线方向上的制导律设计之前,首先简要介绍有限时间理论,方便后续制导律的设计与证明。
定理2 考虑如下非线性系统[9]:
假设在系统原点的邻域U∊Rn内存在一个连续函数V(x,t),并且函数V(x,t)具有一阶连续导数,如果再存在一个大于零的实数α,使得V(x,t)在U 上是正定的,并且使得V˙(x,t)+αVλ(x,t)在U 上是半负定的,其中,λ∈(0,1),那么称系统(18)的原点可以达到有限时间稳定。
因为V(x,t)是正定的,将式(19)左右两边同时对时间t 积分,可以得到
且有
终端时刻tr取决于初始值x(0)=x0,那么有V(x,0)=V(x0),上界满足
其中,x0是系统原点附近某一开域的任意一点,证毕。
在导弹飞向目标的过程中,导弹和目标相对距离的变化率小于零,因此,只要控制视线角的变化率为零,就能保证导弹击中目标[10],同时考虑到有期望终端视线角的约束,选取视线角速率和视线角误差为状态变量,法向加速度为控制输入,具体定义如下:
其中,qθf、qφf为期望的终端视线倾角和视线偏角。
根据三维空间内导弹-目标相对式(6)可以得到状态方程表达如下:
对于上述系统构造滑模面:
式中,s1、s2的表达形式设计如下:
其中,β1、β2=const>0,0<α1、α2=const<1,s1表示纵向运动滑模面,s2表示侧向运动滑模面。
在趋近律方面构造一种自适应滑模趋近律,以保证系统有良好的动态特性:
式中,ε=[ε1ε2]T。它的物理意义是在制导初期弹目相对距离R 较大,趋近滑模面的速率要小,而随着导弹不断地逼近目标,趋近滑模面的速率不断加快,确保导弹在击中目标前系统能够进入滑动模态。
将式(24)两边同时对时间t 求导并将式(22)、式(25)代入可以得到制导律形式如下:
值得注意的是:控制率u1、u2中含有x1和x3的指数项,当x1和x3趋近于0 时会出现奇异问题,因此,采用非线性方法对其进行限幅处理,即:
至此,有终端视线角约束的三维制导律设计完毕,利用式(26)中的制导方法,能够保证三维制导系统(22)在有限时间内收敛到滑模面s=0,并且在滑模面s=0 上系统的状态也能在有限时间内收敛到零。
证明:选取李雅普诺夫函数V1=sTs,显然V1正定。
对V1求导,并将制导律表达式(26)代入,整理得到:
式中,ε=min(ε1,ε2)
由定理2 可知,制导系统(22)能够在有限时间内收敛到滑模面s=0 上。
而在滑模面s1=0 上,有:
选取新的李雅普诺夫函数V2=,显然V2正定。对V2求导,有:
当α1∈(0,1)时,有∈(0,1),根据定理2 可知,系统状态在终端滑模面s1=0 能够在有限时间内收敛到零,同理可证系统状态在终端滑模面s2=0 也能够在有限时间内收敛到零。
3 仿真结果与分析
为了说明本文所设计的三维空间内有终端视线角约束的协同制导律的有效性,接下来针对4 枚导弹同时攻击一个在海平面上作机动航行的舰船这一场景,对制导律表达式(17)、式(26)进行仿真验证,4 枚导弹之间的通讯拓扑结构由图2 给出,4枚导弹的初始位置、初始速度以及所期望的末端攻击视线角如表1 所示,每枚导弹能承受的最大过载为50,g 取9.8 m/s2,仿真步长取10 ms,同时为了抑制滑模态出现抖振现象,用以下的饱和函数来替代符号函数sgn(s),并取δ=0.01。

图2 导弹间的通讯拓扑Fig.2 Communication topology between missiles
目标舰船的初始位置为(5 000 m,0 m,5 000 m),航行速度VT=30 m/s 恒定,初始航迹偏角为10°,并以aT=5sin(0.01t)m/s2的加速度作侧向机动,控制参数选取如下:α1=α2=0.9,β1=0.4,β2=0.2,ε1=ε2=0.2。
4 枚导弹的三维运动轨迹、弹目相对距离、预估剩余飞行时间、沿视线方向的过载nx、纵向平面内沿视线法向的过载ny、侧向平面内沿视线法向的过载nz、视线倾角、视线偏角、视线倾角角速率和视线偏角角速率随时间的变化曲线如图3~图12 所示。

图3 弹目三维运动轨迹Fig.3 3-D trajectory of missile and target movement
由图3 和图4 可以看出,即使起始点位置不同,但在本文设计协同制导律的控制作用下,4 枚导弹依然能够从不同的方向沿不同路径同时击中在海平面上机动的目标。由图5 可以看出,在分布式控制算法(17)的作用下,4 枚导弹在制导初期通过信息交互协调剩余攻击时间,大约在5 s 时各导弹的剩余攻击时间能够达成一致。图6 反映了4 枚导弹沿视线方向的过载随时间的变化情况,过载在前5 s 变化迅速,之后逐渐趋于稳定,这是因为在制导前期需要过载指令的变化从而控制各导弹的飞行速度,进而使各导弹的剩余攻击时间达成一致,实现对目标的协同打击,这与图5 所示的现象吻合。图7 和图8 反映了4 枚导弹沿视线法向的过载随时间的变化情况,为了使视线角速率快速收敛至零,导弹过载在前期指令较大且变化较为剧烈,之后随着视线角速率逐渐趋近于零导弹过载也随之变为平缓并收敛至零,过载曲线光滑且抖振抑制效果明显。图9~图12 表明,在本文所设计的协同制导律的作用下,弹目视线倾角和视线偏角能在有限时间内收敛到期望值,同时,弹目视线倾角角速率和视线偏角角速率能在有限时间内收敛到零。以上的分析结果表明,本文设计的有终端视线角约束的协同制导律,能够保证4 枚导弹以期望的终端视线角同时击中目标,验证了所设计的协同制导律的有效性。

图4 弹目相对距离Fig.4 Relative distancebetween missile and target
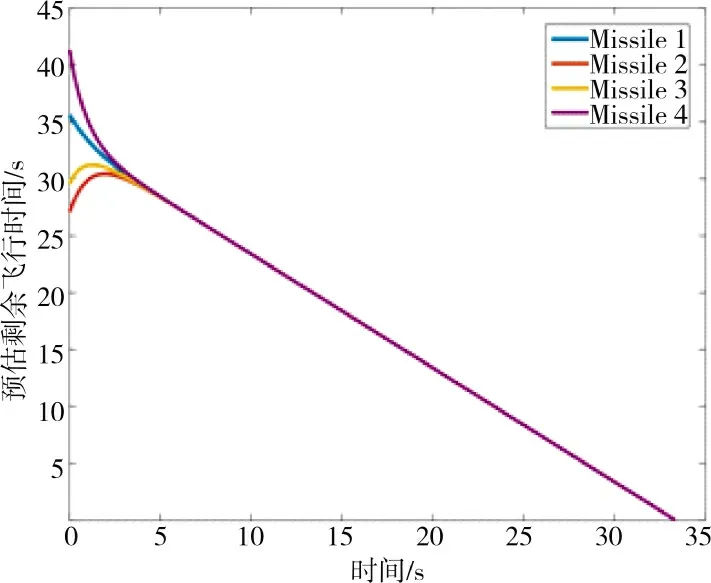
图5 剩余时间Fig.5 Time left
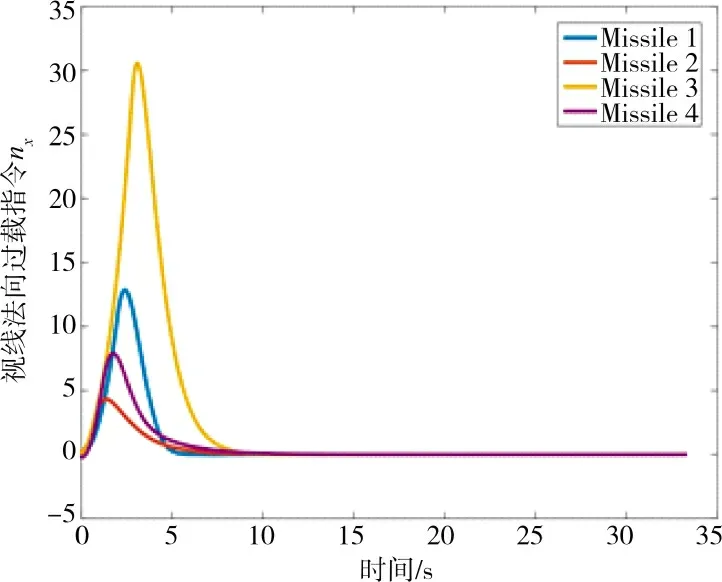
图6 视线方向过载指令nxFig.6 Overload command along LOS
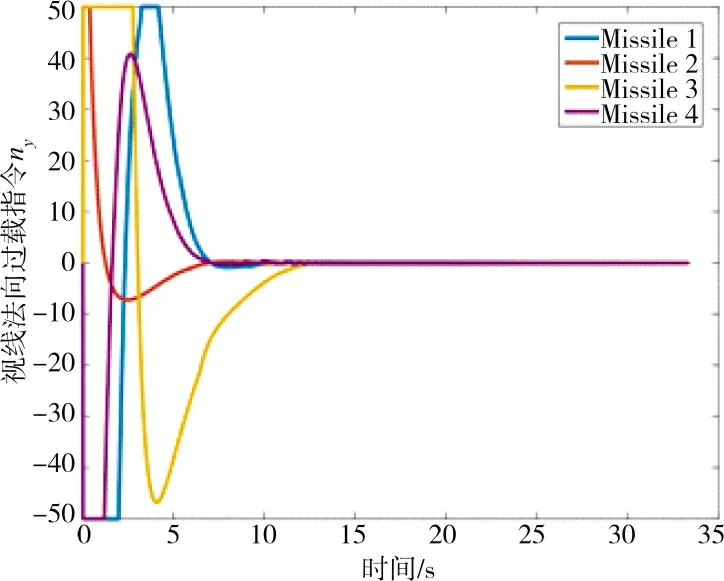
图7 视线法向过载指令nyFig.7 Normal overload command ny of LOS
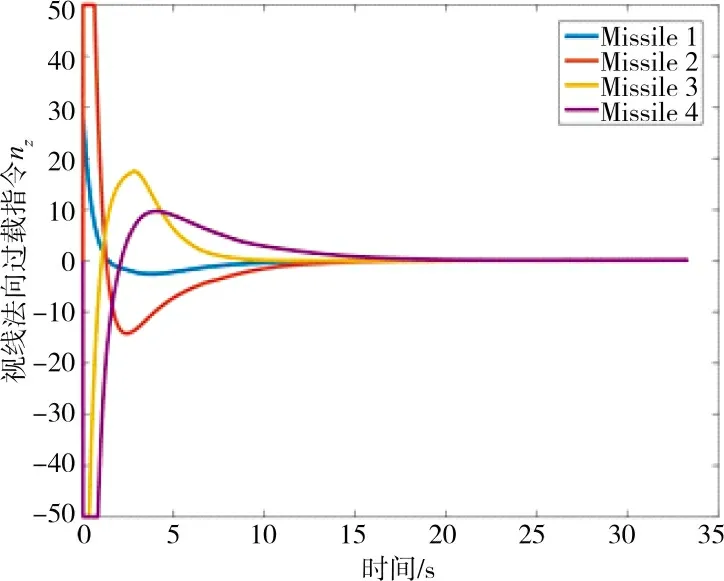
图8 视线法向过载指令nzFig.8 Normal overload command nz of LOS

图9 视线倾角Fig.9 Line of sight inclinationangle

图10 视线偏角Fig.10 Line of sight deflectionangle
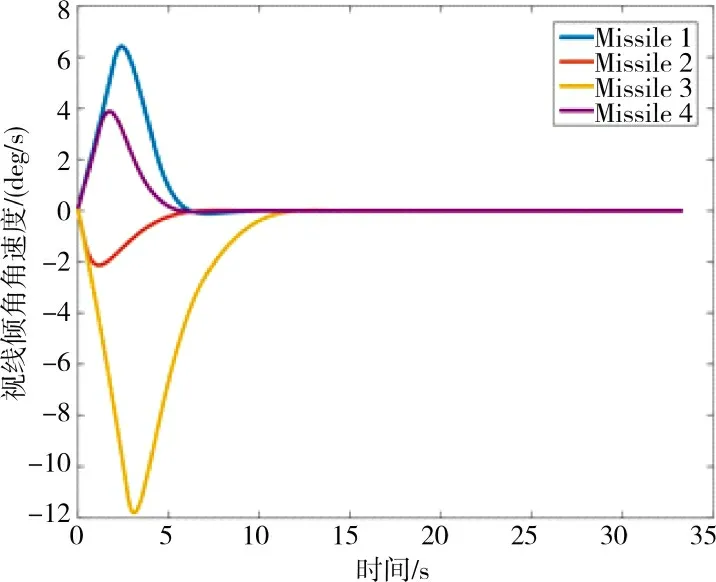
图11 视线倾角角速度Fig.11 Line of sight inclinationpalstance

图12 视线偏角角速度Fig.12 Line of sight deflection palstance
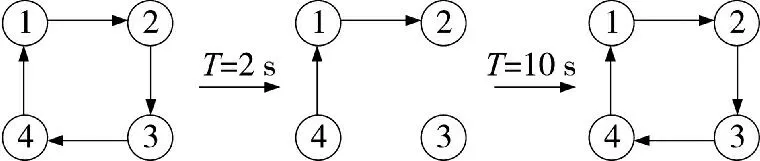
图13 通讯拓扑切换Fig.13 Communication topology switching
以上仿真是假定导弹间的通讯拓扑结构固定不变的,下面考虑拓扑结构切换的情况,文献[11]表明对于一致性算法式(8),即使系统存在随时间切变的拓扑结构,但只要保证每一相邻有限时间隔内所有切换子图的并集存在有向生成树,系统的状态还是能够在有限时间内收敛到一致,只不过子图切换的频率会影响系统的收敛速度。
在以上仿真条件的基础上,假设第3 枚导弹由于通讯故障在2 s 时刻与系统失去链接,在10 s 时刻恢复链接,即导弹之间的通讯拓扑按照图3 所示的拓扑结构切换。
4 枚导弹的弹目相对距离和预估剩余时间的变化曲线如下页图14 和图15 所示。

图14 剩余时间Fig.14 Time left

图15 弹目相对距离Fig.15 Relative distance between missile and target
由图14 可以看出,2 s 时第3 枚导弹与系统失去链接,导致其无法与其他3 枚导弹达成时间一致,10 s 后恢复链接,新的拓扑图存在有向生成树,使得4 枚导弹重新达成时间一致,图15 表明即使系统在时间段内存在无向的通讯拓扑结构图,但在整个有限时间段内系统所有子图的并图存在有向生成树,所以依然能够保证4 枚导弹同时击中目标。
4 结论
本文针对导弹的协同攻击问题,在视线坐标系下建立了导弹-目标相对运动模型,在此基础上基于一致性理论设计了视线方向上的制导律,基于有限时间理设计了视线法向上的非奇异滑模制导律;对所设计的制导律给出了稳定性证明;通过数学仿真实验检验制导律的性能品质。仿真结果表明,所设计制导律能够使得多枚导弹以期望的视线角同时击中目标,具有一定的工程意义。本文考虑了目标机动方式已知的情况,后续可通过设计扩张状态观测器估计目标机动,从而设计考虑目标机动未知情况下的协同制导律。

