基于带约束可能性聚类的多目标跟踪新算法*
刘全仲,李良群
(1.深圳大学ATR 国防科技重点实验室,广东 深圳 518060;2.中国长城科技集团有限公司,广东 深圳 518057)
0 引言
随着现代军事、卫星导航和智能交通等系统的快速发展,多目标跟踪作为相关系统的一项重要的关键技术,越来越受到科研人员和工程实践者的重视[1-5]。为了实现对多个目标进行准确的状态估计和关联,首先需要解决的就是多目标与观测之间的数据关联问题。经过几十年的发展,已经涌现出了大量的数据关联方法[1],如最近邻方法(NN)、全邻数据关联方法(多假设数据关联、联合概率数据关联(JPDA))、模糊数据关联及其一些基于机器学习的数据关联方法等。在实际工程中,用的最多的是最近邻法,该方法简单易行,但在复杂的多目标环境,随着杂波数的增加,关联效率降低。为了处理杂波情况,国外学者提出了著名的联合概率数据关联滤波器(JPDAF),该方法通过引入联合事件,考虑杂波对关联概率的影响,有效提高了关联正确率,但缺点是计算量太大,用于工程实际比较困难。
在目标跟踪中,由于运动模型和观测模型具有很大的不确定性,要对这种不确定性进行建模,在没有更多先验知识的情况下,往往非常困难。模糊数学由于其能够很方便地在算法中引入专家知识,现在已经广泛地应用于目标跟踪,其中,模糊聚类在数据关联中的应用取得了很大的成功[6-8]。实际上,目标与观测的数据关联问题就是要解决哪个观测来源哪个目标的问题,而模糊聚类在这类数据分类问题上表现出了良好的效果。ASHRAF M A 等首次将模糊C 均值聚类(FCM)解决目标观测数据的分类问题[6],在提出算法中,FCM 聚类不需要迭代更新,计算速度快和复杂度低,然而,当目标数合杂波数增加时,关联准确度下降。为此,LI 等在传统JPDAF 的基础上,利用最大熵模糊聚类实现关联概率的自适应计算,提出了最大熵模糊联合概率数据关联滤波器(MEF-JPDAF),在实时性和性能两方面取得了很好的效果[7]。进一步LI 等基于直觉模糊聚类,给出了一种基于直觉模糊聚类的JPDAF 方法,在关联性能上较MEF-JPDAF 有了一定的提升[8]。为了更进一步改善密集杂波下的多目标关联的准确率,利用可能性聚类较FCM 聚类方法能够更有效处理杂波的优势,本文利用目标预测位置作为目标函数的约束条件,构建一种新的可能性聚类目标函数,以此得到目标观测的隶属度矩阵来代替关联概率,提出了一种基于可能性聚类的联合概率数据关联滤波方法,实现对多目标的正确跟踪。
1 JPDAF 及Fitzgerald-JPDAF
JPDA[1]的状态更新方程为:
虽然JPDAF 在理论上比较完善,但在实际应用中,计算量随着杂波、目标数的增加呈指数增长,很难用于实际工程当中。Fitzgerald 在JPDAF 的基础上,提出了一种改进的联合概率数据关联方法,在其方法中,目标观测的关联概率计算如下:
其中,
B 为一正常数。从上面公式可以看出,对于每个目标,所有与之有关的目标观测关联概率的和不为1,这在密集杂波下,多目标跟踪的性能有可能会下降。
2 提出的PC-JPDAF 方法
自FCM 聚类的数据关联方法提出以来,无论理论还是工程上都得到了广泛的应用。该方法简单易行,但在杂波环境中,容易造成杂波与目标的误关联。本章将提出一种带约束条件的可能性聚类新方法,并将其用于多目标跟踪的数据关联中。
2.1 带约束的可能性聚类方法
利用可能性理论,放松FCM 对于隶属度函数的约束条件,RAGHU K 等[9]给出了能够有效处理噪声数据点地可能性聚类方法,定义如下的优化目标函数:
其中,ηi为正常数,加权指数在本算法中等于2,表示样本点到聚类中心的距离。利用拉格朗日乘子法,优化目标函数可得:
其中,K=1。在可能性聚类的基础上,为了更加符合多目标跟踪的实际情况,目标的预测位置一般就在目标实际位置的周围,但同时由于运动模型的不精确以及观测噪声的影响,目标预测位置往往会带有一定的误差。为此,为了更好地优化可能性聚类目标函数,考虑将目标预测位置与实际聚类中心的差值和作为聚类的约束条件,构建如下新的可能性聚类目标函数:
于是,联合目标函数J0和J1,构建如下凸聚类目标函数J 如下:
为了推导出可能性隶属度uij的表达式,对凸聚类目标函数进行求偏导可得:
于是,最后可以得到目标函数的优化结果为:
其中,
其中,I 是Si与同维的单位矩阵,K=1。同时,根据目标跟踪的特点,聚类中心可以选择目标观测的预测值,即
对于航迹i 终结的处理,如果航迹连续3 个周期没有观测进行更新,则认为目标丢失,该航迹就终结,在第4 个周期进入循环的目标数为c-1。
2.2 PC-JPDAF 算法步骤
根据前面提出的可能性数据关联方法,基于可能性聚类的联合概率数据关联滤波器(PC-JPDAF)的具体步骤如下:
Step 2:根据式(16)计算聚类中心V;
Step 3:利用式(15)、式(17)计算隶属度矩阵U;
Step 4:根据2.1 节提出的带约束可能性聚类方法,更新隶属度矩阵U,并用可能性模糊隶属度代替目标观测的关联概率,
Step 5:按式(22)、式(23)对目标状态进行更新,
Step 6:重复Step 1~Step 5,直到完成对目标的跟踪。
3 实验结果与分析
为了评估PC-JPDAF 方法的性能,以均方根误差和算法计算时间作为评判标准,对Fitzgerald’JPDAF[1]、MEF-JPDAF[7]、IF-JPDAF[8]和PCJPDAF 算法进行比较。实验中采用3 条实际飞行轨迹例子,具体情况可以参照文献[8]。每次实验进行100 蒙特卡洛仿真。
目标的运动模型为:
图1(a)给出了目标实际轨迹;图1(b)给出了提出方法的目标估计轨迹。从图1 可以看出,提出方法能够较好实现目标与观测数据的关联和估计。图3 各种算法的目标位置均方根误差对比结果。从图3 中可以看出,在杂波密度为1 的情况下,提出方法要优于Fitzgerald’JPDAF、MEF-JPDAF 算法和IFJPDAF 算法。主要原因有:1)由于提出算法在聚类中引入了目标预测位置作为约束,提高了模糊隶属度计算的准确性;2)提出算法充分利用可能性聚类对杂波的抑制能力,减少由杂波引起的错误关联,可以较准确地对目标观测进行关联,从而实现对目标的实时精确跟踪。
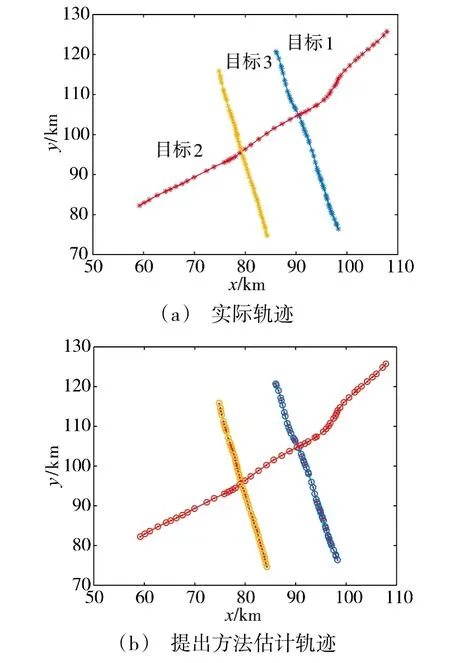
图1 目标实际轨迹及估计轨迹Fig.1 The actual trajectory and estimated trajectory of targets
在实时性方面,下页表1 给出了各个算法的CPU 运行时间对比,表中结果为100 次实验的平均后的一次实验运行时间。从表1 可以看出,MEFJPDAF 算法的运行时间最短,PC-JPDA 算法次之,为0.075 s,基本能够满足对目标的实时跟踪要求。

表1 算法的CPU 运行时间对比(s)Table 1 Comparison of CPU running time(s)of the algorithm
4 结论

图2 目标的位置均方根误差对比图Fig.2 Comparison diagram of root-mean-square error of target position
本文针对密集杂波环境中的多目标跟踪问题,分析了模糊数据关联产生错误关联的原因,提出了一种基于带约束可能性聚类的多目标跟踪算法。本文根据多目标跟踪的实际特点以及可能性聚类对噪声的鲁棒性,以目标预测位置为约束条件构件可能性聚类的目标函数,并以此目标函数进行优化得到目标和观测隶属度函数矩阵,并用隶属度代替关联概率实现目标关联概率的计算,最后给出了算法的具体步骤。实验结果表明,本文方法能够实时有效地对多个目标进行跟踪,具有一定的工程应用价值。

