低空无人机群自组织网络弹性综述

刘继新,张新珏,蒋伶潇,刘禹汐

(南京航空航天大学民航学院,南京 210016)

随着国家低空空域管理改革的不断推进,民用无人机(unmanned aerial vehicles,UAV)飞行需求呈现迅猛增长趋势,并在商业、公共、军事、旅游和体育等领域得到了广泛应用[1]。5G网络建设带动通信领域的快速发展,无人机之间的通信能力得到大幅提升,未来无人机群将比单一无人机拥有更广泛的应用前景[2]。与单一无人机相比,无人机群的群体效益更高,生存能力更强,同时群体协同作业也具有更高的机动性。因此,无人机群在联合侦察、搜索救援、协同作战等任务中具有更广泛的应用[3]。

近年来许多学者对无人机群和其他多智能体系统展开了系统研究[4-5],研究方向主要集中在无人机群拓扑设计[6-8],任务分配[9-11],路径规划[12-16],协同控制[17-19]和规划调度[20-21]等方面。然而,这些研究大多数假定无人机群处于无干扰状态的情况下,仅考虑了无人机群在正常飞行状态下的性能表现。

针对无人机群的外部威胁问题,学者们更专注于无人机群如何避免破坏事件的发生。Peng[13]考虑了无人机群在执行任务期间受到扰动的情况,优化了具有中止策略的联合路由计划,最大限度降低了无人机群的运行总成本。Zhen等[20]对无人机群的初始航迹进行重新规划以避免合作搜索攻击任务期间的潜在冲突。避免外部扰动是提高无人机群运行效率的有效途径,然而这种方法不可能完全防止无人机群受损。由于无人机群具有自适应特性,因此无人机群可通过信息交互自发地适应环境,避免潜在冲突和由于破坏性事件导致的无人机群体损伤。

复杂网络常用于表示各类复杂的群体系统结构,可以将无人机群的运行态势映射至复杂网络模型,通过复杂网络指标对无人机群的损伤进行分析。无人机群的损伤一般发生在物理层面或网络层面,物理级损坏意味着单个无人机被摧毁或部分功能失效,网络级破坏意味着无人机群网络的拓扑结构被破坏。Tran等[22]基于复杂网络对无人机群进行建模,其中,节点表示无人机,连边表示无人机之间的链路连接,移除节点被视为破坏事件,链路重新布线被视为恢复行动,根据其提出的BA(Barabási Albert)无标度网络模型对信息网络弹性框架进行评估,研究随时间变化网络系统抗干扰能力和扰动后的恢复能力,首次将网络弹性的概念应用于无人机群,发现复杂多变的空域环境干扰了无人机群的正常运行,除了受自身内部故障影响外,恶劣天气、飞行物攻击等外部威胁也在一定上程度干扰了无人机群运行安全[23]。在实际应用中,即使无人机群中某些个体发生损伤,整个无人机群也必须确保任务的成功执行,因此对无人机群网络的弹性提出了更高的要求[24]。

无人机智能化和群体化是当前以及未来的研究重点,无人机自组织网络在受到扰动时可以自发进行适应性调整从而恢复群体性能,因此研究无人机群遭受破坏后的动态重构过程对无人机群安全高效运行具有重要意义。鉴于此,着眼于无人机群面对破坏事件后的动态演化过程,阐明无人机群自组织网络弹性的概念,同时总结几种常见的弹性评估方法以及提升网络弹性的措施。

1 无人机群自组织网络弹性相关概念

1.1 无人机群自组织网络概念

研究表明,无线自组织网络是最适合用于无人机群系统协同作业的网络结构[25],因此采用无线自组织网络架构的无人机群网络称为无人机群自组织网络。自组织指无人机群不依赖任何其他设备,各个无人机独立运行,通过相关调度算法自动地组成网络结构。无人机通过组建强伸缩性、高动态性、迅速组网和抗毁能力强的无人机群自组织网络,能够实现高度的群体智能化,协同完成众多单机难以实现的任务。根据控制算法的不同,无人机群自组织网络主要分为两种典型结构:结构一为基于生物群体行为的控制结构[26],结构二为基于领导者-追随者(leader-follower)的分簇结构[27]。

结构一通过个体无人机基础行为的不同组合实现无人机群体智能协作,一些著名的基于群体的无人机群控制算法(如蜂群)得到改进,从而提升了无人机群体效益[28]。基于鸽群的无人机群控制算法中,鸽群中存在着层级领导网络,下层个体鸽子的飞行规律是跟随上层鸽子领导飞行[29]。随着科技水平的不断提高,无人机群的控制方法将逐渐从人为远程控制转变为智能控制,最终发展为与生物群集组织运作相似的完全自主控制模式。最终无人机群理想运行状态如图1所示,即10个无人机节点通过黑色虚线表示的通信链路相连,无人机之间通过自身信息共享执行复杂任务,这种无人机群自组织网络没有固定结构并且变化迅速,具有强扩展性和高机动性,并可通过实时环境反馈及时调整编队状态,但其位置调整过程中可能陷入局部最优情况,不易实现编队整体的全局最优结构。

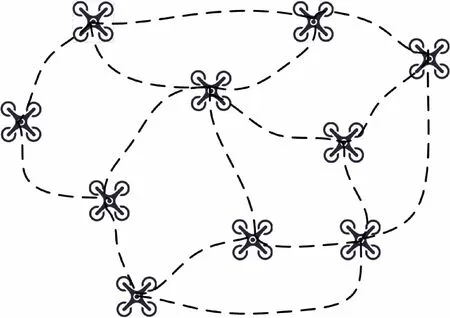
图1 基于生物群体行为的无人机群控制结构Fig.1 UAVs control structure based on biological population behavior

结构二以领导者无人机作为位置和姿态基准,其余无人机作为追随者以领导者为中心跟随其飞行。如果有两个以上的领导者,每个领导者及其追随者将形成一个簇。领导者之间可以相互交流,而每个簇的追随者只能与该分簇的领导者或与其相邻的无人机交流。同时,追随者需感知领导者的运动信息,以调整自己的位置和速度。此外,当领导者受到攻击时,将选择临时领导者接替遭受攻击失效的领导者,以维持整个无人机群的正常稳定运行,如图2所示。这种结构全局协调性好,但是系统容错性、灵活性较差。两种无人机群控制结构对比如表1所示。

表1 无人机群结构特性对比Table 1 Comparison of structural characteristics of UAVs

蓝色无人机表示领导者;黑色无人机为追随者;蓝色虚线表示两个簇的领导者相连;黑色虚线表示其余无人机的连接状况图2 基于领导者-追随者的无人机群分簇结构Fig.2 UAVs sub-cluster structure based on leader-follower

1.2 无人机群系统弹性概念

随着无人机群研究的不断深入,评估无人机群系统的稳定性也成了实际应用中非常重要的研究方向。

无人机群是一个典型的大型复杂系统,主要表现在具有多样层次结构、动态重构特性和各种复杂的编队控制方法。系统的稳定性是一个多样性指标,可以细分成很多不同方面的属性,如鲁棒性、脆弱性、可靠性和弹性等。鲁棒性通常定义为对干扰不敏感,体现在发生破坏事件时保持基本性能的能力[30-33],鲁棒性旨在最大程度减少系统受到干扰后立即出现的性能损失,无人机群的鲁棒性反映了在失去一些无人机后系统维持功能和完成任务的能力。脆弱性集中体现在无人机群系统对已知干扰的敏感性,它衡量了干扰造成的损失或遭受的破坏程度。无人机群具有任务属性,可靠性表示系统在一定条件下确保任务完成率的能力。弹性表示为系统在发生破坏事件后恢复正常状态的能力。弹性度量的常见方法是考虑3种能力:吸收能力、适应能力和恢复能力。吸收能力可以定义为系统能够吸收破坏事件所造成的影响并尽可能减少影响程度的能力;适应能力可以定义为系统通过经历一些变化来适应不良情况的能力;恢复能力可以定义为系统从破坏性事件中恢复并快速回弹到正常或预期性能的能力。

相比于其他评价系统稳定性的指标,弹性允许一些性能损失,并且能够评估随着时间的推移系统逐渐恢复预期性能的表现。由于无人机群系统的自适应能力和动态重构特性,弹性概念的引入可以更好的评估无人机群系统状态。无人机群弹性指的是无人机群体在遭受干扰或者破坏后自身及时吸收伤害减少损失,尽快恢复性能至预期最佳水平从而提升任务完成度的能力。基于复杂网络理论建立的弹性指标可以对无人机群抗干扰能力进行评估,继而可以研究不同无人机群性能恢复措施对于系统弹性提升的影响,进而推动了无人机群体智能化的发展。

2 无人机群自组织网络弹性评估方法

2.1 基于复杂网络的无人机群模型

在有关无人机群等复杂系统分析和建模的研究中,已有学者提出了基于Agent的建模、Petri网方法、系统动力学、复杂网络等理论方法。这些方法在建模复杂系统时都非常有效,可以分别适配于不同系统的场景应用。其中复杂网络理论的主要优势之一在于它能够识别系统基本单元连接结构中的普遍属性[34]。系统可以用复杂网络来描述,其中节点代表组件,边表示节点之间的物理或逻辑连接[35]。该方法已广泛应用于电网[36]、基建设施[37]、交通系统[38]和制造业[39]等领域。

一般来说,基于复杂网络对无人机群建模的方法是把集群中的单个无人机视为节点,各无人机之间的联系视为边。无人机群的动态变化可以视作复杂网络模型中节点和连边的变化[40]。在无人机群遭受干扰或者破坏的阶段,通过随机或者根据节点的度、介数、集聚系数等特征[41]定向移除节点或者是边,建立无人机群动态变化的模型。

根据复杂网络建立简化的初始无人机群自组织网络结构示意图G={V,E},其中,V为节点,E为连边,如图3(a)所示。在无人机群遭受破坏阶段,移除被干扰的无人机即失效节点vi和邻居节点vj与之相连的边{vi,vj}∈E,虚线表示被破坏的节点和边,如图3(b)所示;在无人机群恢复阶段,红边为剩余节点之间重新连接的边,如图3(c)所示,该过程即为无人机群的动态重构。

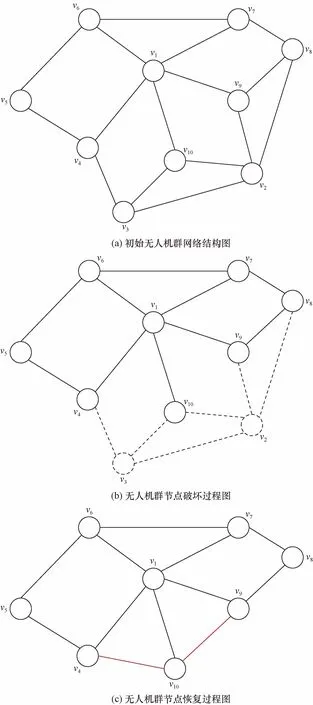
虚线表示被破坏的节点和边;v1～v10为节点图3 无人机群系统建模Fig.3 UAVs system modelling

无人机群建模过程本质是对集群网络的演化进行分析,图3展示了简单无人机群网络模型的变化过程,但在实际应用环境中,由于无人机群系统中复杂的信息交互和动态关系,需要考虑多方面因素,例如任务分配、无人机性能、网络拓扑设计、合作协同策略、信息交换融合策略和攻击恢复策略等[42]。将无人机群进行不同层面的拆分耦合,Wang等[43]提出对无人机群分通信层、结构层、任务层三层相互依存的网络模型:通信层中,将每架无人机视作通信点,无人机之间的通信链路可视作边;结构层中,将每架无人机自身视为节点,无人机之间的物理距离视作边;任务层中,每架无人机可以承载不同类型的有效荷载,将有效荷载表示为节点,边表示为具有相同权重的有效荷载之间的连接。因此无人机群网络模型不仅要映射到复杂网络理论,还要赋予其实际物理层面的意义,从而可以进一步根据现实扰动评估无人机群体弹性。

2.2 无人机群弹性评估曲线

无人机群的弹性评估提供了比其他性能评估更独特的视角,不仅考虑无人机群吸收破坏的能力,还考虑恢复和重构能力。相较于鲁棒性等其他性质,弹性度量更全面地考虑了无人机群体状态,不再局限于抗毁性分析,实现对无人机群更加全面的评估分析,同时通过弹性研究可以进一步构建更具恢复能力的无人机群结构。

无人机群在被破坏过程中的经典性能变化曲线如图4[42]所示。

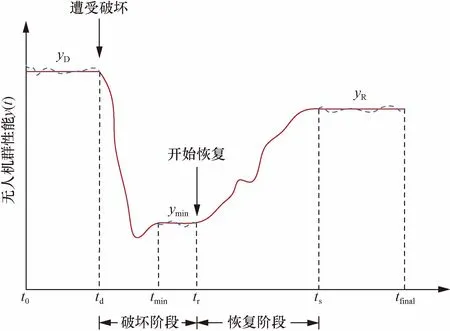
t0初始时间点;td为开始遭受破坏时间点;tmin为性能稳定最低时间点;tr为开始恢复时间点;ts为性能恢复至稳定水平时间点;tfinal为结束时间点 图4 无人机群性能变化曲线[42]Fig.4 Performance change curve of UAVs[42]

根据破坏事件的发生时间点和恢复时间点,将系统性能的动态变化分为破坏和恢复两个阶段。在t0时刻,无人机群保持正常峰值性能yD;在td时刻,无人机群开始遭到破坏,无人机群性能开始下降;在tmin时刻,无人机群性能下降至稳定最低水平值ymin;在tr时刻,无人机群通过自组织执行恢复策略后逐渐恢复性能;在ts时刻,无人机群恢复至稳定状态yR直到tfinal。

2.3 无人机群性能度量指标

无人机群性能一般指集群执行或完成指定任务的能力,集群中无人机间通过内部互相通信实时反馈交流获得信息,因此衡量无人机群性能的指标可认为是执行任务的能力ye(t)和任务绩效ym(t)之和,即y(t)=ye(t)+ym(t)。

第一种能力类型ye(t)反映无人机群执行任务的瞬态能力,一般以无人机群自组织网络性能相关参数或者是无人机群内部交互的信息流量作为计量指标。

Wang等[44]在评估无人机群的鲁棒性时,通过分析无人机群网络拓扑结构的基本指标,分配不同权重后得到综合性性能指标ye(t)。Wang等[45]根据渗流原理评估无人机群可靠性时,引入网络脆弱性和连通性来表示无人机群任务层中的ye(t),当网络不断受到攻击时,任务层网络的连通性降低,完成任务的概率也随之降低。Cheng等[42]将无人机数量和其周边无人机数量映射到复杂网络中节点数量和节点度的概念,以此衡量无人机群执行联合侦察任务的瞬态能力ye(t)。Zhang等[46]将无人机节点定义为正常、过载和失效3种不同状态,根据工作节点与失效节点的比例来定义ye(t),具体数学表达式见式(1)。

(1)

Tran等[22]利用各时刻无人机群接收到的消息数量来反映无人机群的瞬态通信能力ye(t),并且这种能力侧重在系统抵抗破坏和恢复性能的过程中。Bai等[47]基于Tran等[22]的工作,使用无人机群中接收或传递的总信息量表示ye(t),从而进一步考虑在通信距离限制下的无人机群网络结构。

第二种能力类型ym(t)指无人机群在执行不同任务时,从开始到当前时刻的累计任务绩效。在军事作战搜索攻击任务中,ym(t)为战场监测覆盖率和已发现目标的生存时间[48];在联合侦察任务中,ym(t)指通过无人机群累积搜索目标区域获得的全部信息量[42];在搜寻救援任务中,ym(t)可以通过幸存者数量和搜救时间或搜救总效率来表示。

2.4 无人机群弹性定量指标

在早期工作中,有学者通过分析网络拓扑结构相关参数来评价网络稳定性,比如可承受最大故障节点数[49]、受破坏后的最大连通子图相对大小[50]、各种图形度量[51](如链路密度、平均节点度和群集系数)。然而这类方法并未考虑无人机群实际运行时的复杂环境,因此不能简单以网络拓扑参数评价无人机群运行态势。

近年来,有学者提出复杂网络综合指标[44]以及考虑网络性能[45]来衡量无人机群系统性能,通过无人机群的性能累积变化的鲁棒性指标或可靠性指标来评价无人机群系统。但是上述工作仅仅简单地展现无人机群网络遭受破坏后的性能丢失过程,没有进一步探究系统恢复过程,无法完全体现无人机群系统的弹性。

有学者已经提出了几种适用于不同复杂系统的弹性度量方法。Nan等[52]提出了评估相互依存基础设施恢复能力的通用弹性度量。Tran等[22]提出了用于评估信息交换网络的通用弹性度量,如图5[22]所示,颜色越浅的节点度值越大,中心处浅黄色的节点度值较大,边缘浅绿色的节点度值较小,使用无标度模型创建复杂网络,网络通过添加节点而增长,其中网络中节点总数量N=100,初始网络节点数量m0=5,m=2表示每个添加的节点与网络中的两个现有节点连接。

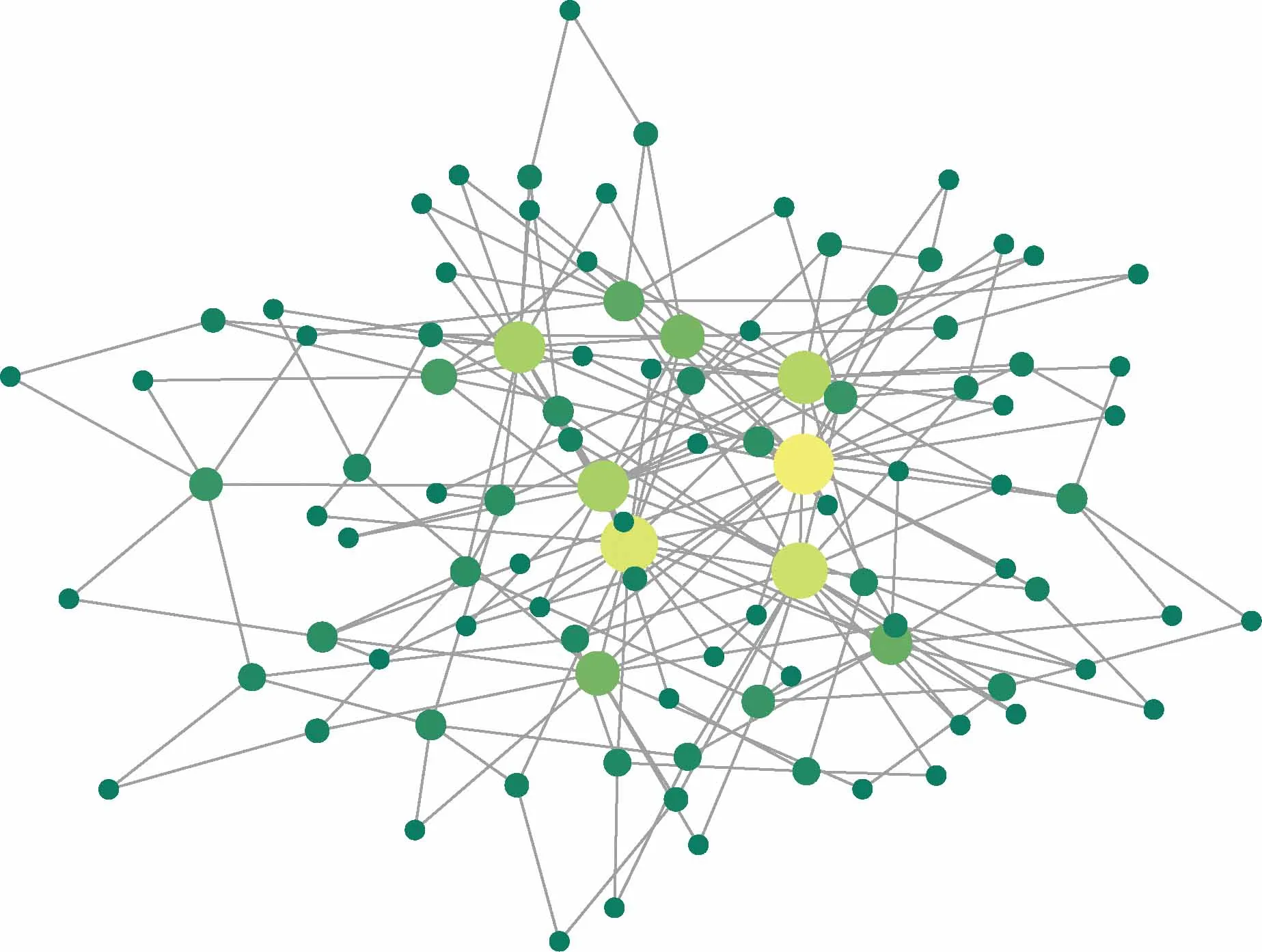
颜色越浅的节点度值越大,中心处浅黄色的节点度值较大,边缘浅绿色的节点度值较小图5 基于networkx的无标度网络模型[22]Fig.5 BA network model based on networkx[22]

其中Tran的工作在无人机群自组织网络的领域中得到了很多的应用,研究提出了弹性总度量R,见式(2),考虑到网络的波动性,设置波动因子ζ、弹性系数(包括总性能系数σ、吸收系数δ)、恢复系数ρ和恢复时间因子τ,表达式如式(3)～式(6)所示。

(2)

(3)

(4)

(5)

(6)

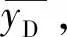
(7)

式(7)中:μt为在t时刻每架无人机生成信息的概率;μ0为无人机群初始信息生成概率;Nt为当前无人机数量;N为无人机总数。

(8)

(9)

(10)

Cheng等[53]基于Tran等[22]的工作提出了一种改进的弹性评价指标,以吸收能力和恢复能力的总和形式构建弹性总度量,并对其分配权重系数,根据各种系统需求增强公式灵活性,其研究中所提出的弹性总度量RI如式(11)所示,考虑过程、后果和时间因素来衡量系统弹性的吸收和恢复能力。破坏过程因子δd用于捕获系统性能的动态行为,破坏后果因子σd用于捕获系统的吸收能力,破坏时间因子ρd用于捕获系统的吸收速度。类似地,恢复过程因子δr、恢复后果因子σr和恢复时间因子ρr分别用于捕获系统在恢复阶段的动态行为、恢复能力和恢复速度,各因子表达式如式(12)～式(17)所示。此项研究成果在无人机群联合侦察任务的情景中得到了应用[42]。

RI=αδdσdρd+βδrσrρr

(11)

(12)

(13)

(14)

(15)

基于绝对时间尺度,上述工作对时间因子ρ进一步深入研究分析,并将其纳入弹性度量中,以量化时间对系统性能的影响。参考基线B是根据不同系统要求提供的参考时间标度。对于基础设施系统,B通常以小时计算,而对于生态系统,B则以月或年为单位计算。

ρd=ΔB/(tr-td)

(16)

ρr=Δ(ts-tr)/B

(17)

式中:Δ为降解因子,用于度量时间维度的相对重要性。

目前的几种网络建模与弹性度量方法如表2[22,42,44-47]所示。在后续的工作中,可以在上述研究基础上进一步对无人机群成本效益和威胁概率进行分析。例如,在已知具体威胁可能性的情况下,上述工作无法确定是否增强吸收或恢复能力能够以经济的方式提高系统弹性。此外,由于两种能力的求和形式以及权重系数的分配占比从而导致所提出的弹性度量指标缺乏足够的理论支撑,这些问题将在未来的研究中通过改进弹性度量方法来得到解决。

表2 不同文献的网络建模与弹性度量方法比较[22,42,44-47]Table 2 Comparison of network modeling and elasticity measurement methods[22,42,44-47]

3 无人机群自组织网络弹性提升措施

无人机群在执行任务时经常遭受破坏攻击或出现机身故障,这使得一些无人机节点无法与其他无人机进行信息交互。在无人机群结构设计时考虑网络弹性可以提高无人机群执行任务的效率,增强无人机群抗干扰能力,进一步扩大无人机群的应用范围。

3.1 吸收能力提升措施

在无人机群遭受破坏的阶段,采用提升系统吸收破坏能力的调整策略,在最大程度上减少无人机群的损伤范围和程度,让群体性能尽可能保持初始状态。

第一种策略是对无人机群自组织网络拓扑结构进行优化,常见的方法是通过分簇算法有效提高网络的能效。分簇算法是指通过一定规则(例如距离相似度)将复杂的无人机群网络划分为几个包含若干无人机的分组,每个分组称为一簇。分簇算法可设定不同的分簇目标,如减少网络的能量消耗[54]、增加网络寿命[55]、减少分簇结构变动[56]等。合理分簇可以使每架无人机在任意时刻都能直接或间接地获取信息,从而提高了集群的连通性和吸收破坏的能力[57]。近年来,许多研究致力于将智能算法用于网络分簇,例如以簇头无人机之间的通信延迟最低为目标的K-means++算法[58]、考虑无人机的传输范围和运动速度的CACONET聚簇算法等[59]。

第二种策略是对无人机群自组织网络性能进行优化。由于无人机群通信网络具有高吞吐量、长传输距离等特性,自由空间光通信(free space optical communication,FSO)也因此应用于无人机通信网络。然而FSO链路容易受到外界干扰影响,因此引入链路状态预测有助于改善无人机通信网络对破坏的吸收能力[60]。无人机群网络链路随时间变化的特性使其预测难度增加,许多网络链路预测方法是利用历史网络信息预测下一时刻的网络结构,比如基于共同邻居的链路预测[61],但是对于历史信息少的无人机群该方法并不适用,因此如何对历史数据量少、具有时间动态属性的无人机群网络链路预测是未来的研究重点。

3.2 恢复能力提升措施

在无人机群遭受破坏后的恢复阶段,当个别或少数无人机处于失效状态时,可采用提升系统恢复能力的策略,重新让群体性能达到或接近预期的稳定状态。

第一种策略是通过修复节点来提升恢复能力。崔琼等[62]通过节点修复的方式提高网络系统的弹性,但是该方法仅适用于造价较高的简单系统,并不适用于数量大且个体成本低的无人机群。无人机具有一定自修复能力,如果是无人机内部出现可修复的故障,当故障成功修复后,将重新加载任务以恢复群体性能;如果无法修复,则通过协调无人机群中的非重要节点(即边缘无人机或备份无人机)来接替受扰机群中被破坏的重要节点。符小卫等[57]设计了一种分布式递归自修复算法,解决了无人机群网络受扰自修复后队形变化过大的问题。孙沁等[63]针对复杂战场环境下的无人机群,改进了无人机群的弹性恢复因子,提出一种多域协同方法以提高无人机群恢复能力。Qiang等[64]提出了一种自适应的改进鸽群启发式算法,引入基于自学习的候选生成策略和基于竞争学习的预测策略,最大化无人机群恢复能力。Bai等[47]考虑了无人机之间有限的通信距离,通过减少无人机群中孤立节点的产生来增大网络连通性,从而提升系统的恢复能力。当无人机节点发生过载时,会降低其他正常节点的通信效率,从而影响整体无人机群的性能。因此,分析负载平衡对提升无人机群恢复能力非常重要。无人机群协同分配任务时需考虑负载平衡[65-67],当某个节点发生过载时,可以根据既定规则将失效节点的任务分配给其他正常节点,从而提高整体无人机群的恢复能力。Zhang等[46]提出了一种考虑负载平衡的无人机群弹性度量方法,并建立了无人机群的性能模型和负载分布模型,分析了不同网络拓扑结构参数下无人机群的弹性变化。

第二种策略是通过重新连接边来提升恢复能力,Chen等[68]使用中心性度量指标评估了美国西部电网的连通性,同时提出了一种边缘重布线的方法提升网络恢复能力。Tran等[69]提出了通过链路随机重连的方式重构受到攻击的网络,从而提高网络的恢复能力。对于无人机群系统而言,失联的无人机可采用随机连接到距离相近的无人机,或者采取优先重连节点度较高的无人机的定向连接方式,使失联无人机重新加入无人机群,从而让无人机群性能恢复到理想稳定状态。

除上述针对网络中节点和边的恢复策略之外,陈旿等[70]针对蜂群无人机系统,提出了一种可以快速计算节点度分布的链路评估算法从而提升无人机集群的弹性。Ordoukhanian等[71]通过动态效用函数研究了受攻击后无人机群的弹性备选方案的实时评估来提升无人机群的弹性。Chen等[72]结合了博弈论中的子博弈完美均衡的方法提升了无人机群通信网络的弹性。

上述研究通过提升无人机群受到扰动时的吸收能力和扰动后的恢复能力两方面来增强系统弹性,对结构层和通信层的网络模型进行优化,从而实现无人机群遭受破坏时的高稳定性和动态重构时的高恢复性,全面提升无人机群网络的弹性,尽可能降低外部干扰对无人机群系统的影响,保证无人机群任务执行效率与运行安全。

4 未来研究方向

随着通信技术的飞速发展,无人机群的应用范围逐步扩大,由于无人机群具有较强的任务属性,因此弹性作为度量无人机群任务执行效率的关键指标显得尤为重要。然而,无人机群弹性研究工作刚刚起步,中外各种新方法和新技术的出现,为研究无人机群弹性问题提供了支持。基于此,提出3个未来重点研究方向。

4.1 无人机群自组网模型的研究

目前基于复杂网络的无人机群自组织网络模型研究,很少考虑无人机之间物理距离对于通信的影响,当无人机之间的通信距离无法满足整体任务执行要求时,简单的网络模型由于对无人机之间的链路连接要求过于理想化,而导致并不适用于实际环境,因此需要改进无人机之间的连接机制。未来的工作中应综合考虑结构和通信两者的耦合效应,可以进一步融合信息传输速度和范围、网络增长等因素的影响,从而设计实现更加灵活的链路连接方法,并且结合真实环境中更完整细化的无人机群任务场景,如考虑到搜索、攻击和救援等具有移动目标的任务,以及无人机最大转弯角、最大仰角等无人机姿态控制约束,建立无人机群的多样性模型。此外,现有研究中无人机数据多来源于仿真,未来将通过无人机群的实际数据来验证所提出复杂网络模型的有效性,为无人机群的模型构建做出进一步指导。

4.2 无人机群弹性评估指标的研究

目前所提出的无人机群弹性指标大多是对Tran等[22]研究工作的改进,缺少一个较为客观的弹性量化定义,大部分学者都是对现有某种弹性评估方法的改进,缺乏横向全方位的客观考量。此外,弹性评估权衡考虑破坏和恢复两个阶段的系统状态,对于两者的权重系数分配缺少客观定义,因此目前弹性评估方法存在一定主观性,可以通过其他网络属性对其进行补充。未来研究可将提出的弹性指标与鲁棒性、抗毁性和可靠性等属性指标进行定量比较,从多个维度评估无人机群。同时,网络中其他属性指标有更为成熟的研究理论,弹性作为综合考虑无人机群运行全过程的指标,可以汲取其他属性研究中的有效方法进行延伸。Li等[73]提出了一个基于渗流理论的综合框架来评估网络可靠性,与上述所提出的弹性度量相比,可靠性度量是启发式的,这对于无人机群的弹性度量研究提供了新的思路。

4.3 无人机群破坏事件和恢复策略的研究

无人机群会遇到不同类型的破坏事件,有些只会造成小规模的损伤,然而有些可能会造成集群崩溃,比如电磁干扰或饱和攻击会导致无人机群的所有连接突然中断,无人机群的性能会立即降至最低。无人机群能否在此极端破坏状况下恢复预期性能,同样也是未来研究工作的重点。在无人机群遭受破坏后恢复的过程中会提前设定各种恢复策略,在进行策略选取时可能会存在时间延迟,因此无人机群需要反应时间来评估当前状态并选取最佳恢复策略。现有的无人机群性能恢复策略大多关注节点恢复和链路重布线,未来可以研究多种相关因素对于性能恢复的影响,同时分析不同策略的性能恢复强度和恢复时间,通过观测弹性变化曲线的波动,确定最佳恢复策略。

5 结论

无人机群作为低空空域中的重要组成部分,而目前无人机群受到的各种内外威胁问题愈发凸显,无人机群弹性成为研究热点。基于复杂网络理论从无人机群弹性概念、弹性评估方法、提升系统弹性措施3个方面进行全面综述。首先介绍了无人机群自组织网络的两种结构,基于此引入自组织网络弹性概念;其次通过复杂网络对无人机群进行建模并进行弹性度量,引入弹性评估曲线分析了不同的弹性定量指标,总结了目前主要的弹性评估方法;最后从吸收能力和恢复能力两方面分析归纳了无人机群自组织网络弹性的提升措施。在此基础上,针对目前无人机群的复杂网络模型过于理想化、弹性评估指标较单一、面对重大破坏事件策略不足等问题,提出了无人机群未来可能的研究方向,以期能够对后续无人机群弹性研究的发展起到牵引作用。