基于三维多上行先导模型的高建筑物年雷击次数分析

樊佳乐,谭涌波*,余骏皓,林雨荷

(1.南京信息工程大学大气物理学院,南京 210044;2.南京信息工程大学中国气象局气溶胶与云降水重点开放实验室,南京 210044)

随着社会和科技的发展,高建筑物越来越多,高建筑物的雷击灾害逐年频发,对建筑物的雷电防护和雷击灾害风险评估也越发被重视。年预计雷击次数是确定建筑物防雷类别和风险评估中最主要的参数之一,对雷击次数的准确计算是提高建筑物安全性,准确评估雷击风险的基础[1-2]。目前关于建筑物雷击次数的工程计算主要有ProtectionofStructuresAgainstLightning:Part1:GeneralPrinciples(IEC61024-1)[3]、ProtectionAgainstLightning:Part2:RiskManagementforStructuresandServices(IEC 62305-2[4],下文简称IEC标准)给出的具体计算公式;除此之外,一些学者通过闪电观测和数值模拟分析不同情况下雷击特征,从理论的角度研究影响建筑物雷击概率的决定性因素[5-6]。

国际电工委员会(International Electrotechnical Commission,IEC)标准中给出了建筑物雷击次数的经验公式,利用建筑物等效截收面积与所处地区的年平均地闪密度两者相乘得到建筑物年预计雷击次数。根据定义等效截收面积为与建筑物遭受相同雷击次数的等效面积,利用建筑物自身的长宽高计算得出。ProtectionofStructuresAgainstLightning:Part1:GeneralPrinciples(IEC61024-1)[3]首次给出建筑物年预计雷击次数的计算公式,在之后的ProtectionAgainstLightning:Part2:RiskManagementforStructuresandServices(IEC 62305-2)[4]中对年平均地闪密度的估算进行了修改,等效截收面积的计算没有修改。中国《建筑物防雷设计规范》(GB 50057—2010[7],下文简称国标)中所采用的雷击次数计算方法参照了IEC标准中的经验公式。相较于IEC标准,国标中区分了高于100 m和低于100 m建筑物等效截收面积的计算,使得对建筑物雷击次数的计算更加细致。不管是IEC标准还是中国国标关于建筑物等效截收面积的计算公式中均考虑了建筑物自身几何特征对雷击次数的影响,但并没有考虑自然闪电的极性,强度以及空间形态等特征在建筑物雷击事件中所起到的关键性作用[8-9]。标准中的经验公式在一定程度上方便了工程应用,但与闪电临近地面引发多上行先导(upward leader,UL)并选择和其中一个或多个先导连接从而形成回击过程的物理过程还存在一定的差异。

大量观测表明,闪电更容易击中高建筑物,建筑物的高度是影响雷击次数的重要因素。目前,对于高建筑物雷击特征的观测主要有光学观测和闪电定位技术两种手段。Eriksson[10]根据不同高度建筑物观测到的闪电数目推导出雷电击中建筑物的概率公式,并通过年平均地闪密度给出建筑物年雷击次数的经验公式。吴珊珊等[11]利用广州高建筑物雷电观测站6年的光学观测资料进行分析,发现在119次下行地闪中,广州塔附近1 km区域内未观测到地闪,1～3 km范围内随着距离增加下行地闪密度逐渐增加,表明广州塔吸引了周围的下行地闪,且随着距离的增加吸引作用逐渐减弱。光学观测能明确闪电击中建筑物的情况,但由于样本量的有限,导致对建筑物年雷击次数的研究相对较少。除此之外,一些学者通过对闪电定位数据的分析来评估高建筑物对地闪活动的影响。Ngqungqa[12]通过地闪定位数据分析南非两座铁塔附近的闪电活动,发现铁塔周围半径2.5 km内的地闪密度大于2.5～10 km圆环区域的地闪密度,表明铁塔吸引了闪电。Zhang等[13]分析了广州塔附近的地闪定位数据,发现广州塔近1 km半径范围内闪电密度显著增加,而半径1～4 km区域明显减小,推测广州塔吸引了一些下行负地闪。闪电定位的数据充足,却由于精度较差的原因,导致难以明确建筑物是否遭雷击,也较难给出建筑物年雷击次数的经验公式。

模拟仿真是观测研究很好的补充手段之一。许多学者利用放电模型模拟地闪的发展与连接过程,通过敏感性实验,研究各种特征参量在建筑物雷击事件中的影响。Zon等[14]利用二维随机模型模拟了闪电的起始,下行先导(downward leader,DL)的梯阶传播以及始发于地面建筑物的UL,并研究了建筑物的雷击情况,发现建筑物越高雷击概率越大,闪电始发距离越远建筑物雷击概率越小。Petrov等[15]利用三维随机模型模拟闪电放电,探讨了闪电极性以及建筑物几何特性对建筑物雷击概率的影响。谭涌波等[8]利用二维随机模型,通过改变闪电空间形态,研究闪电形态的差异对雷击位置,UL长度以及连接过程形态等参数的影响。这些研究在闪电始发位置相对固定的前提下,给出了影响雷击概率的关键性因子,但没有进一步给出建筑物年雷击次数的计算公式。还有一些研究利用拓展的电气几何模型计算多建筑物不同位置的雷击概率以及附近区域的雷击点分布。结果表明,建筑物拐角和避雷针更容易被闪电击中[16-17]。这些研究对更复杂的建筑物群进行研究,但未能考虑自然闪电的不同特征对雷击概率的影响。Jiang等[18]利用二维随机模型模拟负地闪的发展与连接过程,探讨了高建筑物对雷击点的影响,分析了高建筑物的保护距离,给出了建筑物下行负地闪频次的公式。由于模式为二维随机模型,与真实三维空间存在一定的差异。

综上所述,建筑物年雷击次数是建筑物安全性能评估的重要指标之一,IEC标准和中国国标都给出了各自的经验计算公式,但均未考虑自然闪电特性对这个关键因子的可能影响,而已有的一些科研工作还是以定性的理论探讨为主。如何将建筑物的几何特性与自然闪电的传播特征相结合,在尽可能还原真实雷击物理过程的前提下,给出建筑物年雷击次数的计算公式,仍需要深入研究。鉴于此,在最新搭建的三维高分辨率多先导随机模型基础上进行修改,通过改变建筑物高度,闪电始发的位置以及闪电强度进行大量模拟,分析不同情况下建筑物的雷击概率和年雷击次数。在一定程度上更精细的计算了建筑物的年雷击次数,为高建筑物风险评估提供可靠依据。

1 模式介绍

闪电连接过程的模型涉及到建筑物的高度,宽度等特征,因此需要较高的分辨率才能更精准的还原建筑物的特征以及闪电的空间形态。而DL每往前延伸一步,都需通过迭代技术对空间电位进行重置计算[19],需要耗费大量的计算资源,这也是目前难以实现高分辨率三维闪电连接过程模拟的重要原因[20]。本课题组基于GPU并行计算解决了三维高分辨率泊松方程的求解问题[20],并在此基础上搭建了三维多先导随机闪电连接过程的模式框架[21],考虑了DL在传播过程中毛细分支的退电离过程,让模拟得到的先导能更好地再现真实闪电的空间多分叉且蜿蜒延伸的空间形态。在已有的三维高分辨率随机多先导连接模型的基础上,通过敏感性实验,探讨孤立建筑物年雷击次数的影响因子,最终给出计算公式(模式的基本框架可参考文献[22])。

本文模型不考虑云中放电的部分,只截取闪电到达近地面附近的发展情况,如图1所示。考虑到自然界中负地闪占所有地闪过程的90%以上[23],只考虑负地闪所引发的上行正先导以及它们之间的回击过程。在模拟域顶部设置一段初始的DL,并赋予这段DL一个初始的电位,作为闪电在近地面发展的起始条件。考虑到实际的闪电会从空间中任意位置始发,对初始DL在模拟域顶部的位置做出一些调整(图2)。模式中DL的传播是由通道点与周围环境点的电位差决定,当电位差超过150 kV/m时[18],闪电先导发展。根据观测经验,DL可以产生很多分支[24-25],在模型中允许DL每一个发展点都可以向周围的点发展,再根据周围点的电场值的权重随机选取待发展点[20]。当DL到达近地面时,会从建筑物尖端或者地面引发多个UL,且UL不会有明显的分支,本文模型允许满足UL起始阈值180 kV/m时的建筑物或者地面上的多个格点始发,判断头部点与周围环境点的电位梯度,当满足传播阈值150 kV/m时[18],随机选取一个待发展点发展且只允许UL头部发展。根据观测经验,设置正负先导的速度比为1∶6[26-27]。先导每发展一步都会对全域电位重解,当DL和UL之间两点的电位差大于连接阈值500 kV/m时发生连接[18,28]。实际雷暴过程中,由于雷暴云中存在大量电荷使得环境电场增强,故设置背景电场为-10 kV/m。在模型中,建筑物、地面、先导通道以及模拟域上边界均满足Dirichlet边界条件,模拟域的侧边界满足Neumann边界条件。

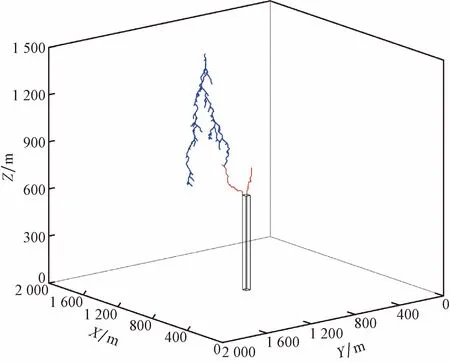
蓝线表示DL通道;红线表示UL通道结构图1 模型示意图Fig.1 Schematic diagram of the model

图2 模拟区域示意图Fig.2 Schematic diagram of simulation area

选取模拟域大小为2 km×2 km×1.5 km,空间分辨率为10 m×10 m×10 m。初始DL长度设为50 m,为了研究不同强度的闪电在建筑物雷击事件中的影响,初始下行负先导内部初始电位设为-20、-30、-40 MV来模拟不同强度的负地闪到达近地面的情况[9,29]。图2展示了模拟区域示意图。大量研究表明,建筑物高度是影响雷击事件的重要因素[11],将建筑物的长宽设为40 m,改变建筑物高度(100～600 m,间隔为100 m),并将其固定在模拟域中心位置,图2中不同高度用不同颜色线条进行标注。考虑到闪电会从建筑物上空任意位置始发,设置建筑物与初始DL位置的水平距离范围为0～600 m,间隔为100 m,形成了6个半径相差100 m同心圆(图2)。在选取DL起始位置时只能取整数点,不能取到一个完整的圆,因此设置每个圆的半径误差在10 m内来取到更多的点,图2中展示了在一组模拟中取到的DL起始点。主要探讨闪电强度(3种),闪电初始位置相对于建筑物的水平距离(7种),以及建筑物高度(6种)对雷击概率的影响,总共有126种方案,每种方案模拟300次。来获得统计上有意义的结果。

2 结果与分析

2.1 模拟结果

随机放电模型能够较好地再现先导通道的蜿蜒延伸、多分叉的空间形态[20],在建筑物雷击过程的模拟中,能更好地仿真DL几何特征对连接过程的影响,有利于探讨闪电的多样性对建筑物年雷击次数的影响。从37 800个模拟结果中选取了6次典型的雷击个例(图3),图3(a)为建筑物只始发一个UL,闪电击地位置唯一确定;图3(b)、图3(c)为建筑物始发了多个UL集中建筑物顶端;图3(d)为DL绕过建筑物顶端始发的UL,击中建筑物侧面从而形成侧击现象;图3(e)为闪电直接击中地面的情形;图3(f)为建筑物虽然始发UL,但并未被击中的情况。而这些模拟的典型雷击个例在以往的观测研究中均有报道[25,30-31],从而验证了LAMM能较好地仿真各种雷击事件。与DL连接的UL的起始点为闪电的接地点,根据接地点位置的不同,将模拟实验结果分为击中建筑物和未击中建筑物两种情形。其中,定义击中建筑物的情形为建筑物触发单个UL并发生连接[图3(a)]、触发多个UL且与其中一个发生连接[图3(b)、图3(c)]以及击中建筑物侧面[图3(d)]。定义未击中建筑物的情形分别为建筑物未触发UL直接击中地面[图3(e)]和建筑物触发UL但未产生连接击中地面[图3(f)]。在未击中建筑物的个例中,一般建筑物较矮时不易触发上行先导,而随着建筑物的增高,上行先导触发概率增大,但其并不与DL连接,从而形成上行未连接先导。

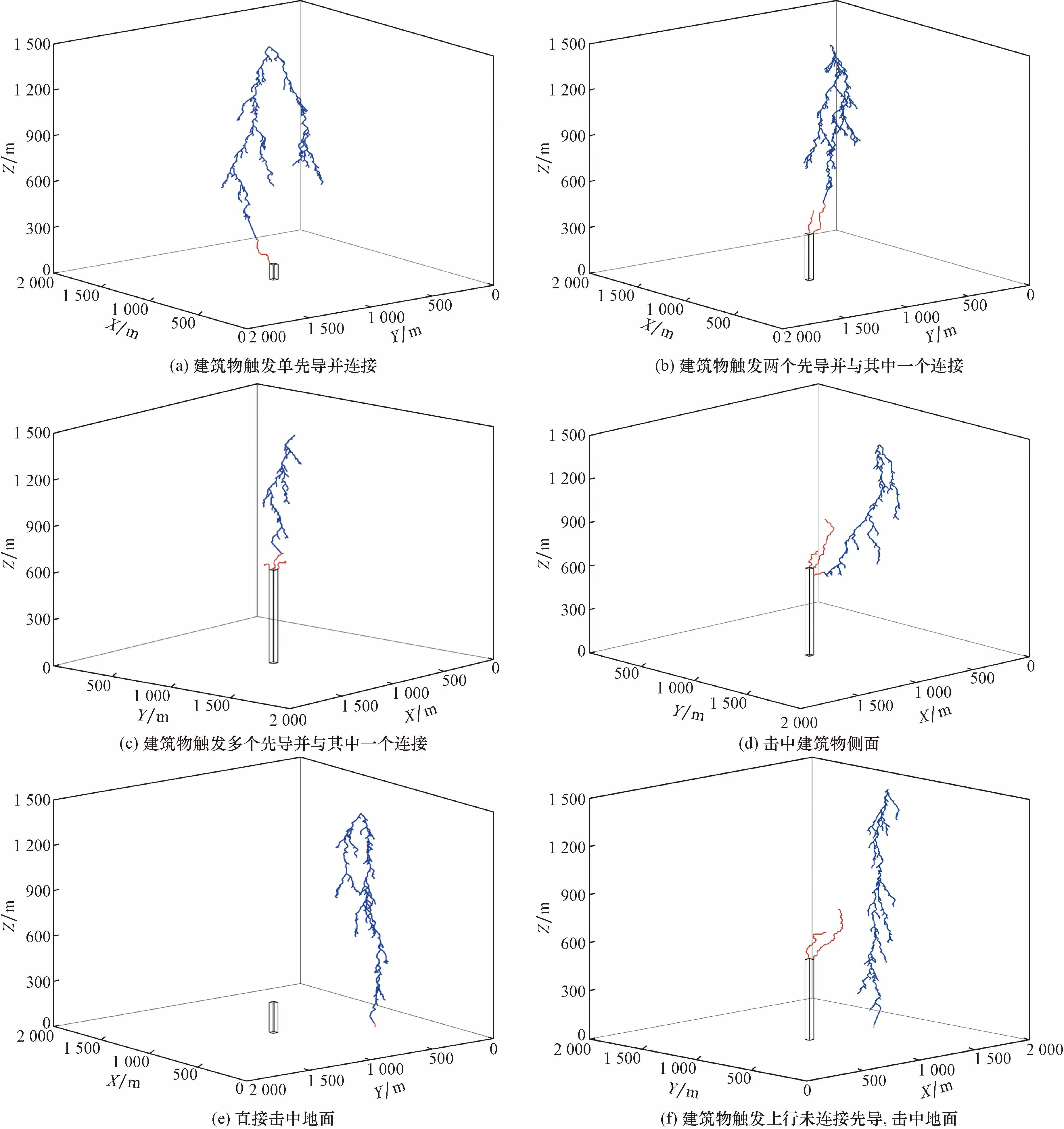
黑色长方为建筑物;蓝线表示DL通道结构;红线表示UL通道结构图3 模拟结果示意图。Fig.3 Schematic diagram of simulation results

在模拟过程中,建筑物高度和闪电始发位置的改变,都会出现不同的雷击特征。如图3(a)～图3(c)所示,DL初始电位均为-30 MV,建筑物高度分别为100、300、600 m,闪电始发位置距建筑物水平距离均为100 m。随着建筑物高度的增加,触发多个UL的概率明显增大。图3(c)～图3(f)中,建筑物高度均为600 m,DL初始电位均为-30 MV,闪电始发位置距建筑物水平距离分别为100、400、600 m。建筑物高度相同时,随着闪电始发位置的远离,偶尔会发生侧击现象,未击中建筑物情况的次数也呈现出增多的趋势。从图3给出的几次典型个例中,不难发现建筑物高度以及闪电始发距离都会对雷击事件产生影响。

为了分析不同强度的闪电对建筑物雷击事件的影响,通过改变DL初始电位进行模拟。以600 m的建筑物为例,图4给出了不同强度的雷击过程模拟结果。图4(a)、图4(c)和图4(b)、图4(d)的初始电位分别为-20 MV和-40 MV,闪电始发位置距建筑物水平距离分别为200 m和400 m。从图4中不难发现,不同强度的闪电在模拟地闪过程中表现出了明显的区别:①闪电初始电位越大,DL的分支越多,闪电发展越旺盛;②闪电强度越大,越容易触发UL,UL发展的长度越长;③随着闪电始发位置的远离,初始电位越小,UL触发时间较晚,使得闪电较难击中建筑物。

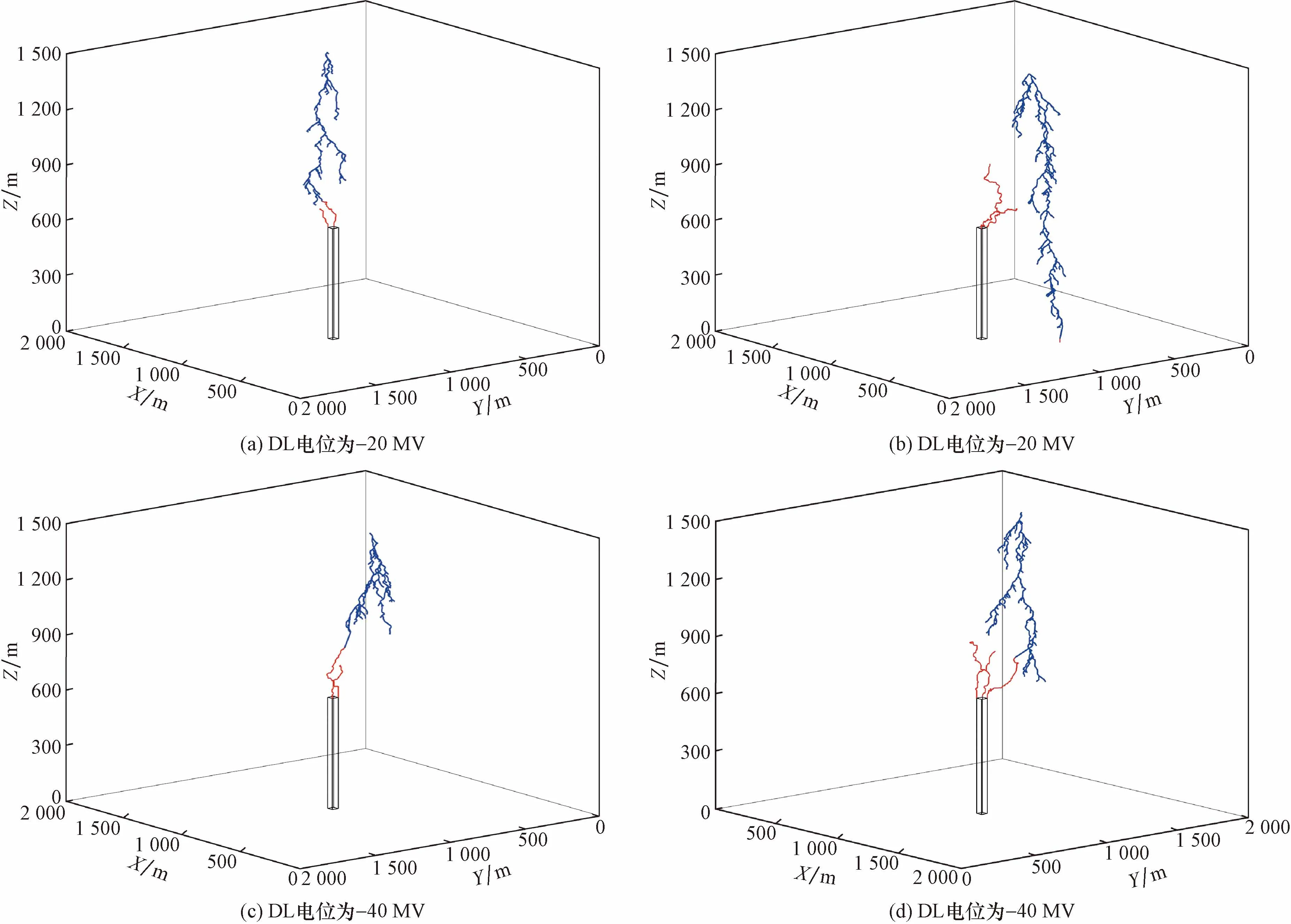
黑色长方为建筑物;蓝线表示DL通道结构;红线表示UL通道结构图4 不同强度闪电的雷击过程模拟结果Fig.4 Simulation results of lightning strike process with different intensities

2.2 建筑物雷击概率与年雷击次数分析

固定DL初始电位为-40 MV,探讨建筑物高度和闪电始发位置对雷击概率以及年雷击次数的影响。根据式(1)计算建筑物雷击概率D[h,r],定义雷击概率是一个相对量,其数值受到闪电始发位置r的影响。

(1)

式(1)中:h为建筑物高度;r为闪电起始位置与建筑物的水平距离;n为当建筑物高度为h,闪电始发位置为r时,闪电击中建筑物的次数;N为该组模拟的总次数,N=300。

图5展现了当DL起始位置与建筑物水平距离为0,100,200,…,600 m时,各高度建筑物的雷击概率,其具体数值用十字符号标出。由图5可知,随着建筑物高度的增加,雷击概率呈现出增大的趋势,即建筑物越高,雷击概率越大。当闪电从建筑物正上方始发时,100 m和200 m高度的建筑物,雷击概率分别为0.86和0.99,其他高度建筑物的雷击概率为1。随着闪电始发位置逐渐远离建筑物,不同高度建筑物的雷击概率呈现出明显差异:其中,100 m和200 m建筑物对应的雷击概率,在闪电始发位置从建筑物正上方远离时,立刻出现递减趋势,而300 m和400 m的建筑物在闪电始发距离大于200 m时,其雷击概率才出现较明显的递减趋势,500 m和600 m的建筑物对应的雷击概率则分别在闪电始发距离大于300 m和400 m时呈现出递减趋势。

由上述分析可知,除了建筑物高度以外,闪电的起始位置也是影响建筑物雷击概率的重要影响因素,在各个高度组下的建筑物雷击概率均随闪电始发距离r的增大而减小。如图5所示,随着闪电起始位置逐渐偏离建筑物,各雷击概率曲线间的间距先增大后减小,这是因为当闪电在离建筑物水平距离很近或很远处始发时,100～600 m建筑物的雷击概率都将趋近于1或0,此时建筑物高度对雷击概率的影响不明显。值得注意的是,闪电起始位置只对雷击概率产生影响,而建筑物的年雷击次数则不受其影响。事实上,建筑物年雷击次数受区域地闪密度的影响,这需要进行全区域的地闪活动分析,后文中将会具体说明。

随着闪电起始位置的变化,虽然不同高度建筑物对应的雷击概率在数值上表现出明显差异,但其变化趋势却呈现出相似的特征。即当闪电在建筑物一定范围内起始,不同高度建筑物的雷击概率都趋近于1,一旦闪电起始位置超过这一范围,雷击概率则会快速下降,而当闪电起始位置距建筑物很远时,雷击概率都趋近于0。根据上述共有特征,选取式(2)对每个高度的建筑物的雷击概率进行线性拟合,拟合结果如图5中曲线所示,得出特定建筑物高度对应的雷击概率曲线fh(r)。表1给出式(2)中的参数a、b、c的数值以及拟合优度R2。

表1 雷击概率拟合曲线公式各参数值及拟合优度计算值Table 1 Parameter values and goodness of fit calculation values of lightning strike probability fitting curve formula

(2)

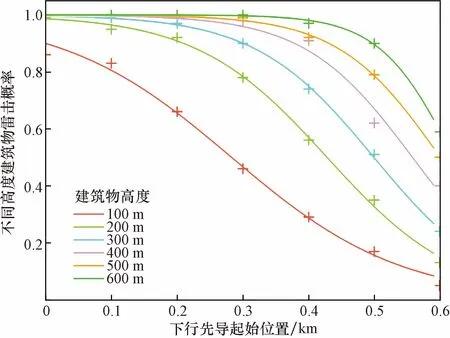
+表示当DL起始位置与建筑物水平距离为 0,100,200,…,600 m 时不同高度建筑物雷击概率的具体数值图5 DL电位为-40 MV时,不同高度建筑物的雷击概率随DL起始点水平距离的变化曲线Fig.5 Lightning strike probability of buildings with different heights varies with the horizontal distance of DL starting point when DL potential is -40 MV

为分析闪电在建筑物上空一定范围内随机发生时雷击建筑物的情况,基于三维多上行先导模型的模拟结果,采用式(3)对建筑物雷击概率进行积分。考虑到闪电始发位置很远时雷击概率都接近于0,并不会对积分后的数值造成影响,选取建筑物周围1.5 km区域的雷击概率进行积分,得到闪电年平均密度为1次/km2/a时,不同高度建筑物的年雷击次数Nh。

(3)

式(3)中:Nh为当区域闪电年平均密度为1次/km2/a时,高度为h的建筑物的年雷击次数;r为DL起始位置距建筑物的水平距离,km;fh(r)为距建筑物不同距离始发闪电时建筑物的雷击概率,其具体计算见式(2)。

根据式(3)计算100～600 m高度建筑物对应的闪电年雷击次数分别为0.39、0.66、0.86、1.33、1.51、1.94,此时DL初始电位为-40 MV。显然,年雷击次数与建筑物高度呈正相关,其中600 m建筑物被负地闪击中的次数是100 m建筑物的5倍。根据计算值,如图5所示进行线性拟合,得出当闪电年平均密度为1次/km2/a时,利用建筑物高度h计算的年雷击次数N的经验公式(适用100～600 m高的建筑物)。

N=1.29×10-6h2+2.18×10-3h+0.16

(4)

图6对比了由式(4)以及国标计算的建筑物年雷击次数。可以看出,所得到的建筑物年雷击次数曲线与国标中给出的具有相同的变化趋势,建筑物高度与建筑物年雷击次数呈明显的正相关。并且随着高度的增加曲线的递增速率均增大,这是由于闪电从较远处始发时,矮建筑物的雷击概率为0,而高建筑物仍有被击中的情况,通过积分得到的年雷击次数会随着建筑物高度的增加而增大。值得注意的是,虽然各高度组建筑物的年雷击次数计算结果均略大于国标的计算结果,但其在一定程度上更符合观测经验。Ngqungqa[12]通过观测得出100 m建筑物的年雷击次数为0.29(本文取0.39),而根据广州塔(600 m)附近1 km范围内未观测到闪电的观测事实[11],推测当闪电年平均密度为1次/km2/a时,广州塔的年雷击次数约为3(本文取1.94)。广州塔是一个尖顶的建筑物,当雷暴云存在时,建筑物顶端的电场畸变更大,使其更容易遭受雷击。所探讨的建筑物都为平顶,计算值略小具有一定的合理性。

图6 DL在高度1.5 km处始发,且闪电年平均密度为1次/km2/a时,不同高度建筑物的年雷击次数Fig.6 Annual lightning strikes of buildings at different heights when DL starts at a height of 1.5 km and the average annual lightning density is 1 strike /km2/a

2.3 改变闪电强弱分析

观测和模拟研究表明,闪电的强弱会影响闪击距离等参数。不同强度的闪电对建筑物雷击概率的影响不可忽略。由于模型中未模拟回击过程,因此无法如观测中利用回击峰值电流判断闪电的强弱,而是通过设置不同的DL初始电位,使得闪电通道与地面形成不同的电势差,以此间接体现闪电的强弱。

设置DL初始电位为-20 MV和-30 MV,统计闪电从距离建筑物不同水平位置始发时,各个高度建筑物对应的雷击概率,并利用式(2)对所得数据进行线性拟合。表2、表3分别给出了这两个初始电位对应的拟合公式中的各参数数值以及拟合优度,并且根据拟合公式绘制不同高度建筑物的雷击概率曲线,如图7所示。

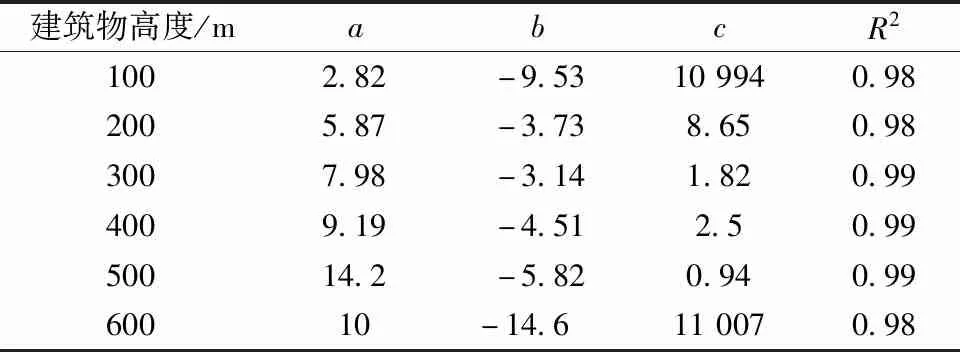
表2 DL初始电位-20 MV,雷击概率拟合曲线公式各参数值及拟合优度计算值Table 2 DL initial potential -20 MV,lightning strike probability fitting curve formula each parameter value and goodness of fit calculation value

表3 DL初始电位-30 MV,雷击概率拟合曲线公式各参数值及拟合优度计算值Table 3 DL initial potential -30MV,lightning strike probability fitting curve formula parameter values and goodness of fit calculation values

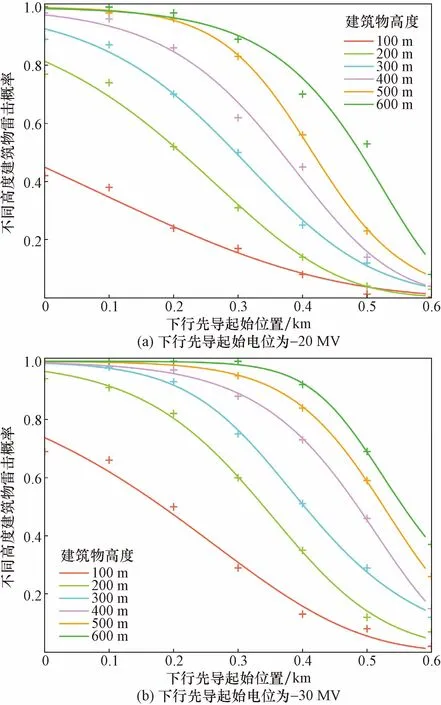
+表示当DL起始位置与建筑物水平距离为 0,100,200,…,600 m 时不同高度建筑物雷击概率的具体数值图7 DL电位为-20 MV和-30 MV时,不同高度建筑物的雷击概率随DL起始点水平距离的变化曲线Fig.7 Lightning strike probability of buildings with different heights varies with horizontal distance of DL starting point when DL potential is -20 MV and -30 MV

图7展示了不同闪电强度下的雷击概率曲线,各图的变化趋势与图5的变化趋势相同。对比图7(a)和图7(b)可知,当建筑物在300 m以下,图7(a)中的每个初始位置对应的雷击概率都小于图7(b)中的雷击概率,在建筑物高度小于300 m以下时尤其明显。而400～600 m建筑物的雷击概率曲线明显比图7(b)中的曲线更早衰减。

根据式(1)分别计算DL初始电位为-20 MV及-30 MV条件下的建筑物年雷击次数,并如图8进行线性拟合,得出利用建筑物高度计算的年雷击次数N的经验公式。式(5)、式(6)分别是当DL初始电位为-20 MV和-30 MV时,特定建筑物高度的年雷击次数N′的经验公式(适用100～600 m高的建筑物)。

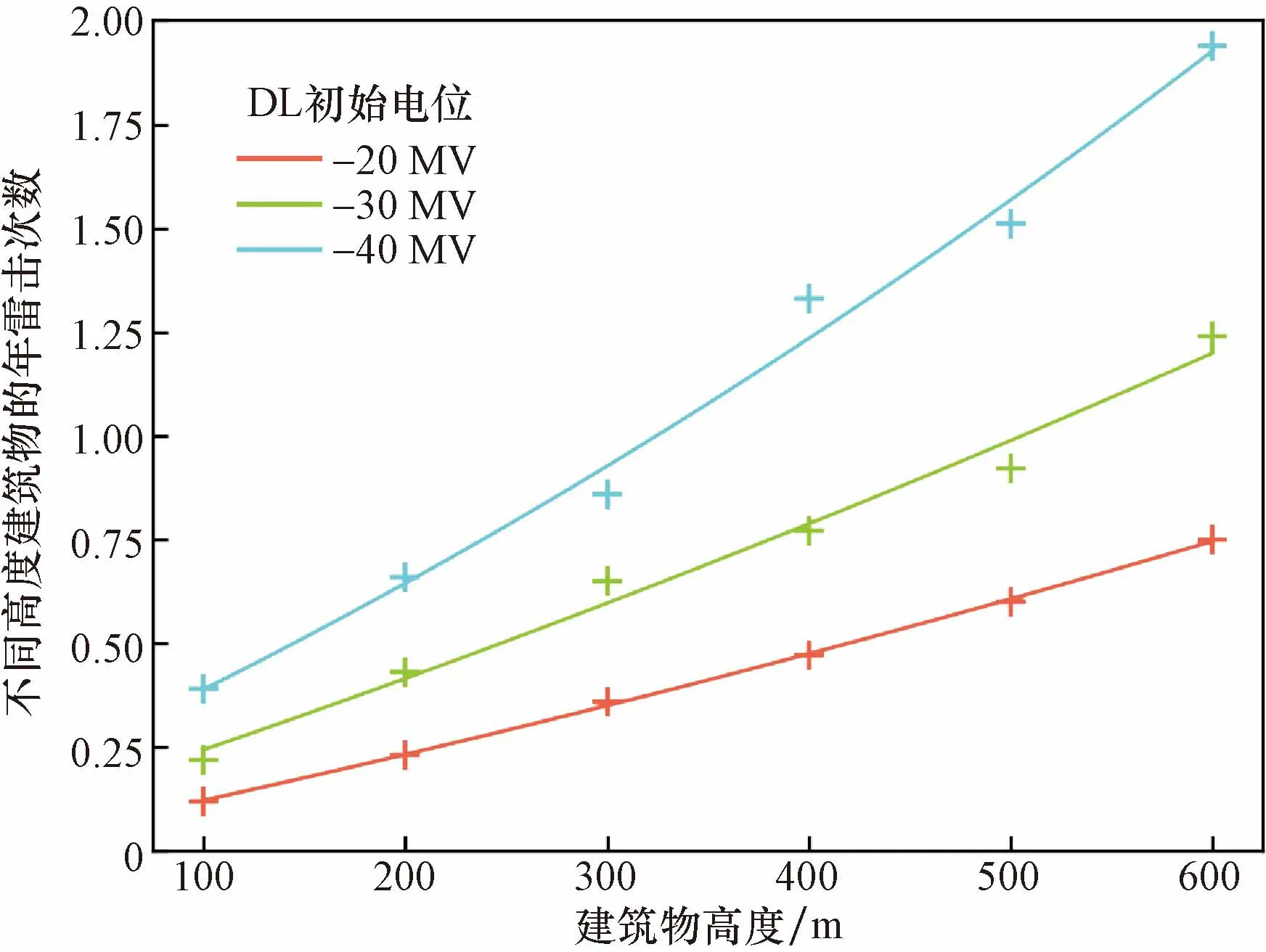
+表示各个高度建筑物的年雷击次数图8 DL初始电位为-20、-30、-40 MV,在高度1.5 km处始发时,且闪电年平均密度为1次/km2/a时,不同高度建筑物的年雷击次数Fig.8 Annual lightning strikes of buildings at different heights when DL initial potentials are -20,-30,-40 MV,starting at a height of 1.5 km,and the annual average density of lightning is 1 strike/km2/a

N′=3.57×10-7h2+1×10-3h+0.02

(5)

N′=4.82×10-7h2+1.57×10-3h+0.08

(6)

如图8所示,当DL初始电位为-20 MV时,100～600 m的建筑物的年雷击次数分别为0.12、0.23、0.36、0.47、0.6、0.75,其中600 m建筑物年雷击次数是100 m建筑物的6.25倍。当DL初始电位为-30 MV时,各高度建筑物对应的年雷击次数为0.22、0.43、0.65、0.77、0.92、1.24,其中600 m建筑物年雷击次数是100 m的5.6倍。随着闪电强度的减弱,高建筑物的年雷击次数与矮建筑物的年雷击次数比值不断增大,这表示低矮建筑物的年雷击次数衰减的程度更大。三组电位对应的年雷击次数均与建筑物高度呈正相关,且随着建筑物高度增加,年雷击次数递增速率不断增大。随着闪电强度的减弱,年雷击次数随建筑物高度增加,其增速明显减小。

通过上述分析,不难发现建筑物高度和闪电强度都是影响年雷击次数的重要因子,二者与年雷击次数之间呈现明显的正相关。为了体现上述因子对年雷击次数的影响,从而得出一个改进的建筑物年雷击次数计算公式,对式(4)～式(6)进行整合。即在不改变建筑物年雷击次数变化趋势的前提下,将闪电的强度引入公式。式(7)为利用DL初始电位和建筑物高度h共同计算的建筑物年雷击次数经验公式。

N′=(0.17x+8)×10-7h2-(0.06x+0.18)×10-3h-(0.007x+0.12)

(7)

式(7)中:x为DL初始电位(适用闪电初始电位为-20～-40 MV);h为建筑物高度(适用于100～600 m建筑物)。

3 结论

(1)基于三维多上行先导模型的模拟,可知建筑物高度,闪电的始发位置以及闪电的强度都是影响建筑物雷击概率的重要因素,随着闪电始发位置远离建筑物,不同高度的建筑物呈现出不同的衰减趋势。

(2)通过对不同高度建筑物的雷击概率进行积分,得出了利用建筑物高度计算的建筑物年雷击次数经验公式。本文计算结果与观测结果较为接近。相较于国标中的公式,更多考虑了闪电本身对建筑物年雷击次数的影响。改变闪电强度进行模拟计算后,得出建筑物的高度和闪电强度都是影响建筑物年雷击次数的重要因素。

(3)本文模型利用闪电初始电位判断闪电强度,而观测中利用回击峰值电流判断,如何结合回击峰值电流判断模型中的闪电强度,需要通过更多的观测资料来完善模型中的参数,使模拟更接近真实的雷击情况。