耦合多孔介质层的内产热腔体双扩散自然对流

胡江涛,蒋文涛,梅硕俊

(1.中南林业科技大学土木工程学院,长沙 410004;2.中山大学大气科学学院,珠海 519082)

由温度梯度与浓度梯度同时驱动的双扩散自然对流广泛存在于自然界与工业应用中,在过去几十年内受到越来越多的关注[1-2]。与纯温度梯度引起的自然对流不同,双扩散自然对流中存在着温度与浓度的扩散且两种扩散之间会有相互作用,从而对流动产生复杂的影响。其中盐梯度太阳池的蓄热过程是一种典型的双扩散自然对流现象[3-4]。在盐池的蓄热过程中,下对流层温度不断升高,上、下对流层存在越来越大的温差与浓度差,最终非对流层的静止状态被打破,导致下对流层发生热逃逸,盐池的蓄热能力降低。为了提升盐池蓄热能力,多孔介质层由于其良好的保温隔热能力,被应用于盐池底部。研究表明,多孔介质层隔绝了盐池底部与地面的热交换,避免了热量损失,蓄热能力提高[5-6]。因此,理解具有多孔介质层的双扩散自然对流机理对于提升盐池蓄热能力是十分必要的。

中外学者对于多孔介质腔体的双扩散自然对流展开了大量研究。Mondal等[7]在均匀和非均匀边界条件下,分析了浮力比对多孔介质空腔双扩散自然对流的影响,描绘了流体流动形态随时间的变化。Lakshmi等[8]在局部热不平衡状态下,分析了矩形与圆柱形多孔介质腔体的双扩散自然对流过程,获得了最适用于蓄热系统的腔体形状。雷鸣[9]分析了两种多孔介质Lattice Boltzmann模型,结果表明,两种模型在稳态不可压流动下均适用。李贝贝等[10]模拟研究了含有高浓度高温圆的多孔介质空腔内双扩散自然对流,探讨了达西数和浮升力比对高温圆表面传热传质效率的影响。邵明芹等[11]模拟研究了多孔介质空腔的自然对流传热,获得达西数、瑞利数等控制参数与传热效率的关联式。张贝豪等[12]模拟分析了倾斜多孔介质腔体的自然对流传热,考虑多孔介质物性参数与空腔倾斜角等因素对传热效率的影响。

熵产最小化是一种新兴的工程系统优化热力学方法,其主要思想是将设计的热力学非理想程度与系统的物理特性(如有限的尺寸、形状、材料、有限的速度和操作间隔的有限时间)联系起来,改变一个或多个物理特性,以优化设计,其特征是在有限尺寸和有限约束下的最小熵产。对于多孔介质腔体的熵产,中外学者已开展大量研究。Mchirgui等[13]分别对多孔介质腔体进行了模拟研究,结果发现降低达西数会增加熵产,而孔隙度对熵产有正面影响。Meshrama等[14]模拟研究了倾斜多孔介质腔体内多个控制参数对熵产的影响,结果表明:腔体倾斜角对熵产有重要影响。Siavashi等[15]模拟研究了倾斜多孔介质腔体内不同热源对熵产的影响,并根据热力学第二定律获得了最佳热源位置。Hussain等[16]对填充纳米流体的多孔介质空腔进行了模拟研究,结果表明:纳米流体的体积分数会促进熵产的产生。Hayat等[17]采用一种改进的达西定律模拟多孔介质腔体的流体流动,考虑了多个控制参数对流动不可逆性与热不可逆性的影响。

近年来,格子Boltzmann方法(lattice boltzmann method,LBM)作为一种介观动力学方法,已发展成为模拟复杂多尺度流动的有力数值工具[18-20]。与有限容积法等传统数值模拟方法相比,LBM不需要处理Navier-Stokes方程中的压力项,计算时间更短。特别是,LBM更容易进行并行计算,在高性能计算机中运行更高效。目前大多数研究仅局限于纯多孔介质腔体,对于部分填充多孔介质的内产热腔体讨论较少。为此,针对盐梯度太阳池,研究多孔介质层对盐池内部双扩散自然对流的影响。将盐梯度太阳池简化为具有多孔介质层的内产热腔体,同时考虑Soret和Dufour效应,采用LBM进行数值模拟。探讨不同内热源强度(R)、达西数(Da)、Soret(Sr)和Dufour(Du)效应作用下流体流动、温度分布与浓度分布,并获得了控制参数对传热传质效率与熵产的作用机理与影响规律,理解多孔介质层对盐梯度太阳池的热盐对流特性的影响,为提升盐池蓄热能力和长期运行稳定性提供理论依据。

1 LBM控制方程

采用不可压格子BGK(Bhatnagar-Gross-Krook)模型,利用3个分布函数fk、gk与hk来模拟研究流场、温度场与浓度场,对应分布函数分别表示为

(1)

(2)

(3)

(4)

(5)

(6)

式中:ρ为流体密度;ε为多孔介质的孔隙率;U=(u,v),其中,u和v分别为速度在x和y方向上的分量;T(x,t)和S(x,t)分别为t时刻x点的温度和浓度;ωk为权重系数;T和S分别为宏观量温度和浓度。

采用D2Q9模型,权重系数ωk和离散速度ck分别表示为

(7)

(8)

考虑多孔介质的力项Fk表达式为

(9)

(10)

G=g(βTΔθ+βSΔs)

(11)

式中:F为考虑多孔介质的外力项;G为浮力项;k为9个方向;c为格子速度;K为多孔介质的渗透率;βT和βS分别为热膨胀系数和质膨胀系数;Δθ和Δs分别为温差和浓度差。

因此,宏观的流体密度ρ、速度v、温度T与浓度S分别表示为

(12)

(13)

(14)

(15)

式中:T和S分别为宏观量温度和浓度;ΦT和ΦS为温度源项和浓度源项。

考虑Soret、Dufour效应与内产热的源项ΦT、ΦS分别表示为

(16)

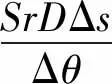
(17)

式中:Du和Sr分别为Dufour效应和Soret效应参数;α和D分别为热扩散系数和质扩散系数;Ti,j和Si,j分别为位置(i,j)上的温度和浓度。

2 模型描述与程序验证

2.1 模型描述

如图1所示,以盐梯度太阳池的热盐对流现象抽象以下模型:将盐池简化为高宽比为0.5的内产热矩形腔体。腔体由流体层与多孔介质层组成。其中,流体层具有强度为Q的内热源,多孔介质层厚度为d。腔体底面为高温高浓度(Th,Sh),上壁面为低温低浓度(Tc,Sc),垂直壁面均为绝热且不可渗透。

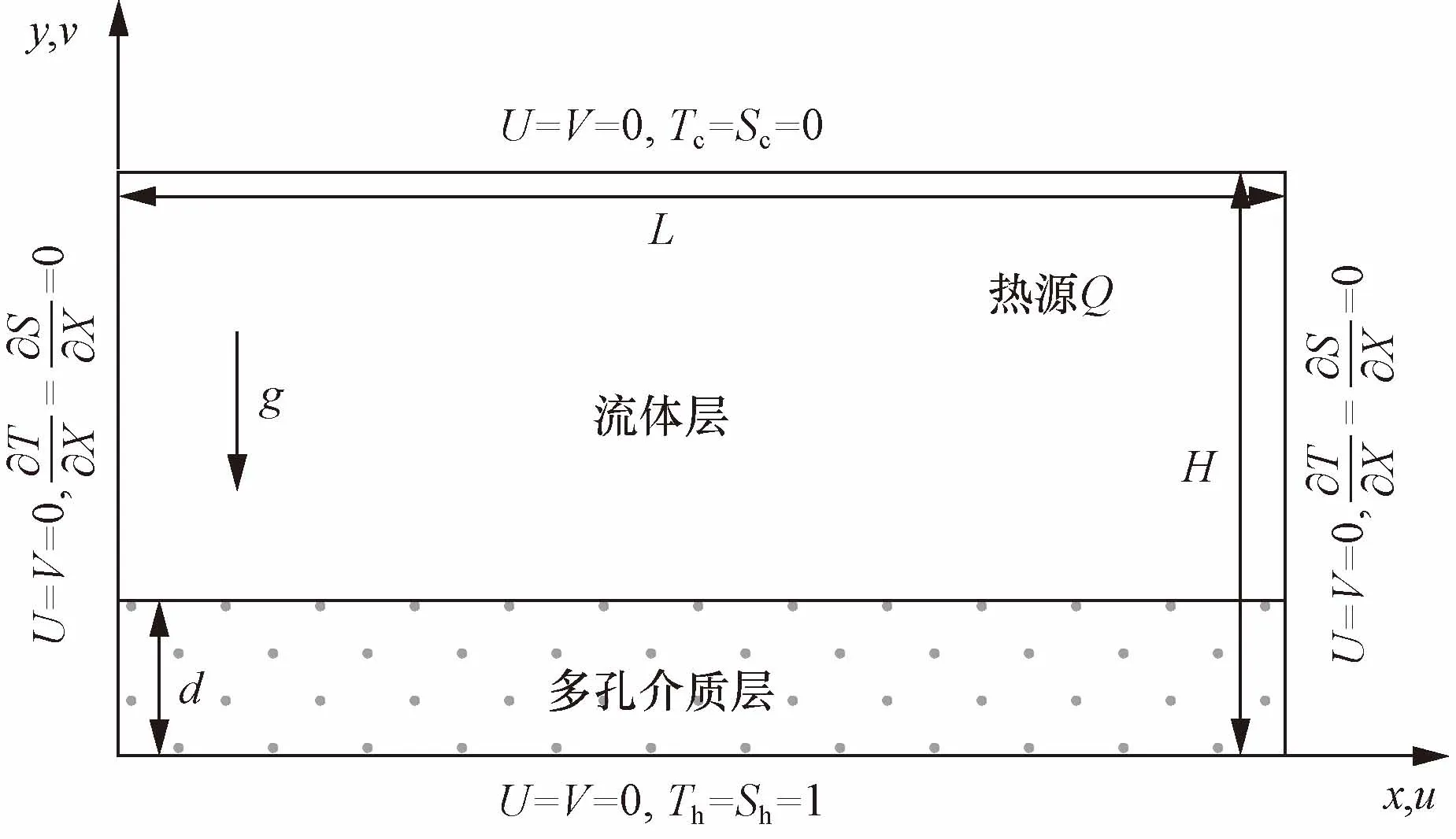
图1 物理模型示意图Fig.1 Schematic diagram of studied configuration

图1中,腔体的高宽比为H/L,多孔介质层的厚度为d,流体层厚度为H-d,其中包含强度为Q的热源。腔体的底面温度(Th)和浓度(Sh)较高,顶面温度(Tc)和浓度(Sc)较低,并且垂直壁面均为绝热绝质壁面,可表示为

Y=0,U=V=0,Th=1,Sh=1

(18)

(19)

(20)

采用底面的平均努塞尔数(Nu)和舍伍德数(Sh)来评估该腔体的传热传质效率,其表达式分别为

(21)

(22)

局部熵产(SL)由流动不可逆性(SF)、热不可逆性(SH)和质不可逆性(SD)组成,其表达式分别为

SL=SF+SH+SD

(23)

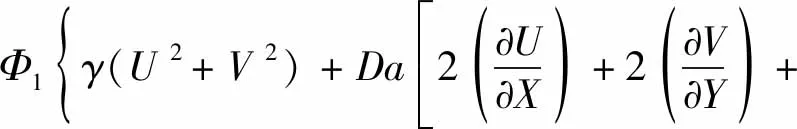
(24)

(25)

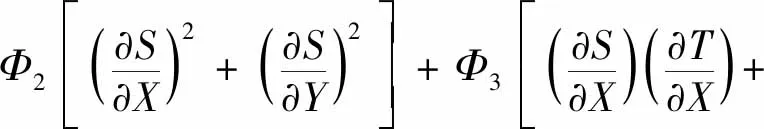
(26)

式中:γ用来区分多孔介质层与流体层,即γ=1对应多孔介质层,γ=0对应流体层;不可逆比Φ1、Φ2、Φ3分别取0.01、0.5和0.01[19-20]。

由此可得,总熵产(STL)与Bejan数(Be)分别表示为

(27)

(28)

2.2 网格独立性与程序验证

在R=0、Da=10-3、Sr=Du=0条件下,选取5种均匀网格100×50、120×60、160×80、200×100与300×150进行网格独立性分析。如图2所示,当网格为200×100时,平均努塞尔数(Nu)与舍伍德数(Sh)的数值不再随网格的增大而变化,此时可视为网格无关性。因此,选用200×100的均匀网格。

微流控芯片的整体结构如图1所示,包括PCB板、集成阵列电极的微流道及接口等。芯片通道入口选用“Y”型,方便不同种类细胞的混合和分离。芯片主通道上分布3个多电极阵列截面,用于主通道内部的电阻抗成像检测。PCB板中印刷了芯片所需的电路,电极通过分布在PCB板两侧的插针接口与其他仪器进行信号传输,芯片的基板则通过螺钉和固定板固定在PCB板中。

图2 平均努塞尔数Nu和舍伍德数Sh的网格独立性Fig.2 Grid independence of average Nusselt and Sherwood numbers

选取相似问题进行程序验证。首先,本文程序与对Soret效应作用下的内产热空腔进行对比验证。如表1所示,误差小于3%,所得结果与文献[18]吻合良好。其次,本文程序与多孔介质方腔的熵产进行验证,如表2所示,误差小于4%,所得结果与文献[13]吻合良好。

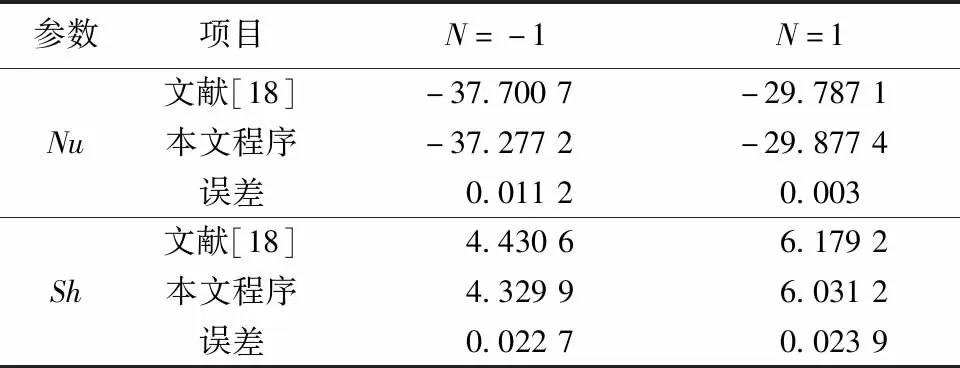
表1 Soret效应作用下内产热方腔内不同浮升力比平均努塞尔数Nu和舍伍德数Sh验证Table 1 Validation of average Nusselt and Sherwood numbers in an internal heating enclosure with Soret effect

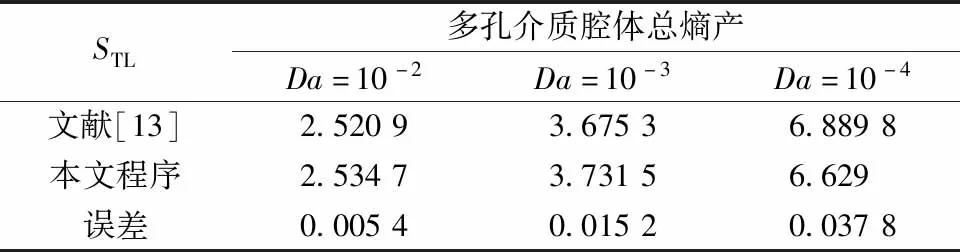
表2 不同Da数下多孔介质腔体总熵产验证Table 2 Validation of total entropy generation inside a porous enclosure with various Da

3 结果与分析

3.1 传热传质特性

内产热强度对腔体内流动与传热传质过程的影响如图3所示。在图3(a)中,此时腔体内无内产热,腔体内部形成4个对称的涡,包括两个顺时针与两个逆时针流动,均位于流体层中。同时,多孔介质层内无流体流动,形成温度与浓度边界层,说明多孔介质层内传热方式以导热为主。当内产热强度增大时,如图3(b)所示,腔体中心的温度升高,这导致腔体中心的两个涡逐渐增大,靠近垂直壁面的两个涡逐渐减小。当内产热强大继续增大时,在图3(c)中可明显观察到靠近垂直壁面的涡已消失腔体内形成两个对称流动方向相反的涡,腔体的整体温度升高,最大温度由底面迁移到了腔体中心。

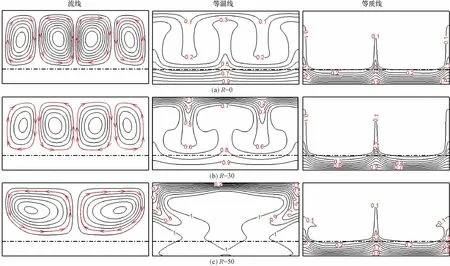
图3 不同内热源强度的流场、温度场和浓度场图Fig.3 Fluid flow,temperature and concentration fields with the variation of internal heat generation

达西数对腔体内流动与传热传质过程的影响如图4所示。当达西数较小时(Da<10-3),此时多孔介质引起的黏性阻力较大,多孔介质呈现固体的特性。由图4可知,Da=10-5与Da=10-4的结果相似,腔体内形成4个均匀分布的涡,多孔介质层内部流体处于静止状态同时底面形成温度边界层与浓度边界层。当Da增大至10-3,多孔介质引起的黏性阻力减小,多孔介质层内出现微弱的流动。此时,在流体层内产热的作用下,腔体流体的流动强度增强,靠近垂直壁面的涡逐渐变小,流体流动的增强同时导致腔体中心的温度与浓度逐渐增大。当Da增大到10-2时,此时多孔介质的黏性阻力可忽略不计,腔体内流动强度得到极大增强,这导致靠近壁面的涡消失,腔体内形成两个对称且流动方向相反的涡。腔体中心的温度和浓度增大,说明Da的增加极大地增强了腔体内部的传热传质过程。因此,多孔介质层对于腔体内的传热传质过程有很好地抑制作用,但盲目减小达西数对结果的影响并不大。

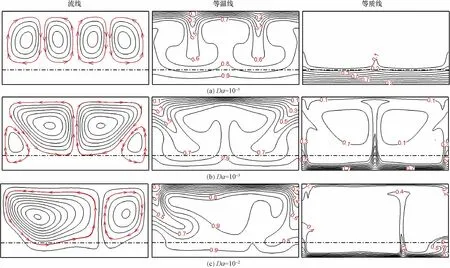
图4 不同达西数的流场、温度场和浓度场图Fig.4 Fluid flow,temperature and concentration fields with the variation of Darcy number

达西数Da与内产热强度R对平均努塞尔数Nu和舍伍德数Sh的联合影响如图5所示。由图5可知,Nu与Sh均随Da的减小而减小,并且在低达西数(Da<10-3)的工况下,Nu与Sh几乎不在变化。这说明多孔介质层对于腔体底面传热传质过程具有良好的抑制作用。在低达西数(Da<10-3)的工况下,随R变化的Nu曲线呈现单调递减的趋势,而Sh曲线基本保持不变。Da=10-4时,R由0增大到50对应的Nu减小了90%,而Sh的变化小于5%。这是由于腔体的温度受到内产热作用会逐渐增大,且最大温度会由底面向中心位置迁移,这导致底面的传热效率减小。同时,低达西数的多孔介质黏性阻力较大,底面形成稳定的质边界层,因此Sh几乎不受R的影响。在高达西数(Da>10-4)的工况下,随R变化的Nu与Sh曲线均呈现单调递减的趋势。Da=10-2时,Nu与Sh分别减小了77%与22%。这是由于高达西数时,腔体内流体流动强度增强,内产热的增强使得底面传热传质效率均减小。

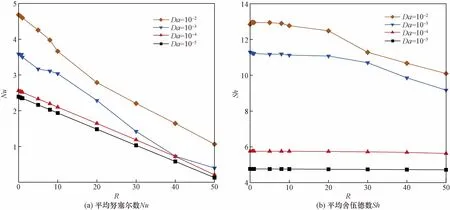
图5 不同达西数下平均努塞尔数Nu与舍伍德数Sh随内产热系数的变化规律Fig.5 Average Nusselt and Sherwood numbers with varying internal heat generation for different Darcy number

Soret与Dufour效应对腔体传热传质过程的影响如图6、图7所示。由图6可知,随着Sr的增加,浓度场有显著变化。当Sr=0.2时,Soret效应较小对腔体内的流动与传热传质影响较小,流场、温度场与浓度场均没有显著变化。当Sr增大到0.8时,多孔介质层内的质边界层被破坏,等质线从底面逐渐向腔体中心迁移,腔体中心的浓度上升。特别是Sr增大到1时,腔体中心浓度继续上升,且更多的等质线集中在腔体中心。这说明Soret效应对腔体的传质过程有极大的促进作用,但对传热过程没有显著影响。由图7可知,随着Du的增大,腔体的整体温度升高并且涡面积变大,腔体的最高温度逐渐高于底面温度。这意味着Dufour效应促进了内产热对腔体温度的升高,从而增强了腔体内流体的流动强度与传热过程。对比可知,在内产热腔体内Dufour效应的作用大于Soret效应。

图6 不同Soret效应的流场、温度场和浓度场图Fig.6 Fluid flow,temperature and concentration fields with the variation of Soret effect

图7 不同Dufour效应的流场、温度场和浓度场Fig.7 Fluid flow,temperature and concentration fields with the variation of Dufour effect

Soret与Dufour效应对平均努塞尔数与舍伍德数的影响分别如图8、图9所示。图8中,随着Sr的增加,Nu几乎保持不变,并且Sh呈单调递增的趋势。这说明,Soret效应只对传质效率有促进影响,而对传热效率无明显影响。随着R的增加,Sh曲线呈单调递减趋势,最终在R=50时重合。这是由于R增加,内产热产生的热浮升力与质浮升力产生对抗作用,从而抑制了Soret效应对传质效率的促进作用。由图9所示,随着Du的增加,Nu不断增大,Sh几乎保持不变。这说明Du只对腔体底面的传热效率有促进作用,对传质效率无显著影响。另外,在Du=0时,Nu随R的变化曲线为单调递减的。然而,随着Du的增加,Nu曲线的变化趋势发生改变,并且在Du>0.5的工况时,Nu曲线呈单调递增的趋势。这是由于Dufour效应极大地增大了底面传热效率,并且在Du>0.5时,Dufour效应的增强作用大于内产热的抑制作用,此时的Nu随R的增加而增大。因此,在这个盐梯度太阳池抽象的腔体内,Soret与Dufour效应对流动与传热传质过程的影响是显著且不可忽视的。

图8 不同Soret效应、平均努塞尔数与舍伍德数随内产热系数的变化规律Fig.8 Average Nusselt and Sherwood numbers with varying internal heat generation for different Soret effect

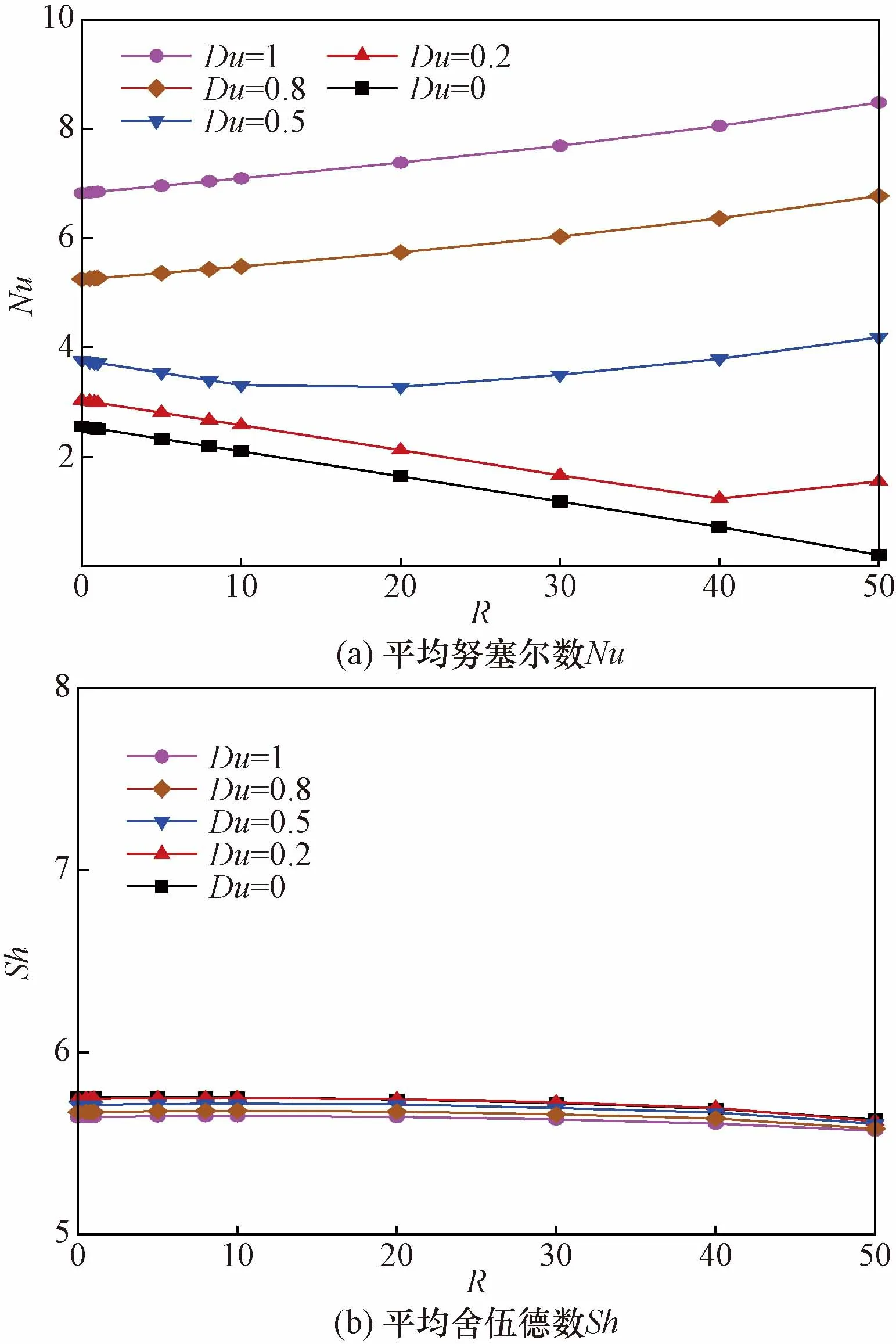
图9 不同Dufour效应,平均努塞尔数与舍伍德数随内产热系数的变化规律Fig.9 Average Nusselt and Sherwood numbers with varying internal heat generation for different Dufour effect

3.2 熵产分析

达西数与内产热强度对腔体总熵产与Be的联合影响如图10所示。可以看出,STL与Be随R增加的变化曲线呈单调递增的趋势。这是由于R的增加导致热不可逆性极大地增加,并且在R>30时,热不可逆性远大于流动不可逆性与质不可逆性,从而Be超过0.5。另外,可观察到Da的增加会导致STL的增大。这是由于高达西数(Da>10-4)会促进了流动与传热传质过程,从而高达西数的多孔介质层会产生较大的熵产。同时,Da的增加导致Be的减小,并且在Da=10-3时Be达到最小值。这是由于Da的增加导致多孔介质层内的流体流动极大地增强,此时热不可逆性的占比减小。但当Da增加到10-2时,热不可逆性的占比增加,从而Be增大。因此可知,多孔介质层对熵产最小化有积极的作用。

图10 不同达西数,总熵产与Bejan数随内产热系数的变化规律Fig.10 Total entropy generation and Bejan number with varying internal heat generation for different Darcy number

Soret与Dufour效应对腔体总熵产与Bejan数的影响分别如图11、图12所示。在图11中,随着Sr的增加,R<30的范围内STL没有显著影响且Be略有增加。这是由于Soret效应对传质过程有促进作用,导致质不可逆性增加,而流动不可逆性减小。

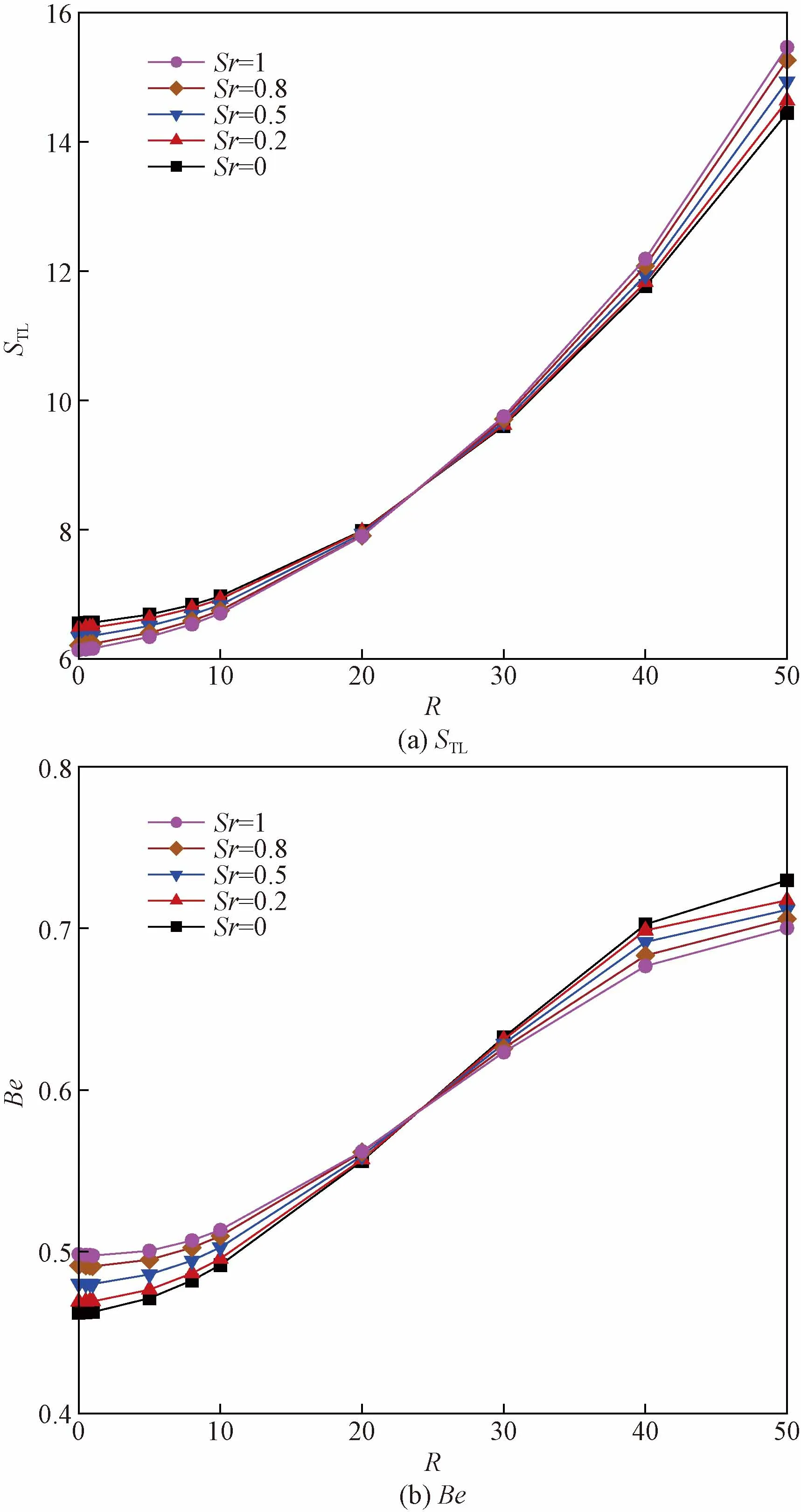
图11 不同Soret效应,总熵产与Bejan数随内产热系数的变化规律Fig.11 Total entropy generation and Bejan number with varying internal heat generation for different Soret effect

图12 不同Dufour效应,总熵产与Bejan数随内产热系数的变化Fig.12 Total entropy generation and Bejan number with varying internal heat generation for different Dufour effect

而R>30的范围内,STL出现增大而Be减小的趋势。这是由于随着R增加,内产热产生的热浮升力与质浮升力产生对抗作用,腔体内的传质过程被抑制,质不可逆性减小而流动不可逆性增加,此时,在Soret效应作用下总熵产增大而Bejan数减小。另一方面,如图12所示,Dufour效应极大增加了总熵产与Bejan数,且在Du>0.5时,Be远大于0.5。这是由于Dufour效应对流体腔体内的流动与传热过程有显著的影响,流动不可逆性与热不可逆性得到极大地增加,并且在Du>0.5时,热不可逆性的增加远大于流动不可逆性,从而Bejan数不论R为多少都远大于0.5。同时,Dufour效应促进了内产热对传热过程的积极作用,从而R越大,STL曲线的增加幅度越大。在R分别为30和50的工况下,Du从0增大到1时,STL分别增加了40%和42%。由图11、图12可知,由于内产热的存在,热不可逆性在总熵产的占比远超于质不可逆性与流动不可逆性,因此Soret效应对熵产的影响较小,而Dufour效应的影响较大且不可忽略。

4 结论

(1)多孔介质层对腔体内部传热传质过程有很好地抑制作用,低达西数(Da<10-3)可减小腔体底面的传热传质效率。多孔介质层对熵产最小化有积极作用,低达西数有助于抑制熵产的产生。内产热强度对熵产有促进作用,总熵产随内产热强度的增强而增加,并且在高内产热强度(R>30)的工况下,Bejan数高于0.5,热不可逆性处于主导地位。

(2)Soret与Dufour效应对腔体内部的传热传质过程有显著的影响。增强Dufour效应会促进内产热对腔体内部传热过程的积极作用,故高Dufour效应(Du>0.5)工况下,传热效率随内产热强度的变化呈单调递增趋势。Dufour效应对熵产有显著的影响,而Soret效应作用不明显。高Dufour效应(Du>0.5)的工况下,Bejan数远高于0.5,热不可逆性在总熵产的占比远超于质不可逆性与流动不可逆性。