半开放式的多车场移动充电车路径优化

周长影,张圣忠,陆迪,白雪

(1.长安大学运输工程学院,西安 710064;2.长安大学经济管理学院,西安 710064)

在技术进步和政策扶持的双重影响下,新能源汽车产业迅速发展,并被广泛应用在出行和货运领域。截至2021年12月底,中国新能源汽车保有量累计784万辆,占汽车总量2.60%。随着新能源汽车应用场景多元化,充电服务需求大幅提升,但充电桩数量不足、布局不合理等问题依然存在,不同程度加剧了新能源车主的里程焦虑。在此背景下,移动充电平台应运而生,移动充电服务的典型模式是依托充电车对在路上因电量不足抛锚的新能源汽车进行救援服务,相较于固定充电站充电的模式,能够减少顾客里程焦虑,提供更加灵活方便的上门充电服务,有效补充城市新能源车辆的充电服务网络。

移动充电平台使用的充电车为电动车,受自身行驶里程约束,需要科学规划充电车的服务路径。目前有关移动充电车路径优化的文献较少,且主要基于单车场模式。Cui等[1-2]引入带时间窗和多模式的移动充电车问题,建立以行驶距离最短为目标的模型,并对充电车电池容量、服务效率等进行敏感性分析。陈萍等[3]考虑顾客软时间窗、充电车里程限制等约束,建立平台收益最大的数学规划模型,将移动充电车服务路径归纳为团队定向问题,开展新能源移动充电车的路径优化研究。

单车场独立服务模式适用于顾客点分布集中的情形,而新能源汽车应急充电服务对需求响应速度要求高。已有城市配送路径优化的相关文献表明,多车场联合配送能提高物流效率,尤其是半开放式的多车场联合服务能高效处理顾客需求,即松弛车辆必须返回原车场的闭环限制,服务结束后的车辆可返回任意车场。移动充电服务具有类城市配送的特征,故移动充电平台可构建半开放式的多车场移动充电车路径优化模型。马冰山等[4]研究了物流配送模式下多车场半开放式联合服务,证明多车场和半开放式路径结合能显著降低物流配送总成本。范厚明等[5]提出了半开放式的多物流中心联合配送模式,表明该模式能快速响应顾客生鲜需求,提高产品配送效率。凌海峰等[6]在开放式车辆路径基础上,考虑多车场和时间窗约束,通过模型求解,证明半开放式的多车场联合服务能提高顾客满意度。刘长石等[7]针对多物流中心共享信息资源模式,建立了总成本最小的开放式车辆联合配送路径规划模型。叶勇等[8]为提高城市配送效率和交通运输服务水平,通过Solomon多组算例对比验证算法求解的稳定性和高效性。周毅君等[9]考虑成本最小和完工时间最短等因素,建立柔性的作业车间调度模型,通过标准算例对问题进行求解。韩孟宜等[10]考虑时间窗惩罚最小和成本最低等约束,求解突发事件下应急物资的最优调度路线,合理解决应急状态下的供需不平衡问题。张瑾等[11]考虑车容量和时间窗约束,建立总成本最小和客户满意度最大的双目标模型,通过实际算例求得问题解并验证算法有效性。姜彦宁等[12]通过遗传算法求解共享车辆和共享车辆分拨中心的整车物流配送问题,证明共享资源配送模式优于传统的单中心配送模式,能够显著节约配送成本。

基于此,考虑应急服务点分布随机性特征,将移动充电车置于多车场联合服务场景,提出半开放式的多车场移动充电车路径优化问题,设计分支定界法和遗传算法求解小中规模算例,以验证模型正确性和算法有效性。研究成果丰富了新能源汽车只能在固定充电站进行充电的研究理论,为移动充电平台总成本降低和移动充电车资源优化提供一定的理论意义。

1 半开放式的多车场移动充电车路径问题

1.1 问题描述

移动充电平台有固定数量的多车场提供联合服务,每个车场有足够数量的移动充电车,能够满足N个应急服务点的全部充电需求。每个应急服务点有一个最佳时间窗[ei,li],ei为应急服务点能够接受的最早服务时间窗,早于该时间时,充电车等待,产生等待成本;li为应急服务点能够接受的最晚服务时间窗,晚于该时间时,要给予应急服务点补偿,作为惩罚。车场提供移动充电车的充电服务,即充电车从车场满电量出发。目标是如何规划移动充电车的数量和服务路径,使得移动充电平台在满足全部应急服务点充电需求的前提下总成本最低。移动充电服务流程图如图1所示,移动充电平台收到应急服务点请求,直接派出移动充电车对其提供服务,移动充电车在特定时间内完成服务并返回任意车场。半开放式的多车场移动充电车路径优化问题示例如图2所示,该例子中有3个车场提供联合服务,共派出4辆移动充电车满足9个应急服务点的全部充电需求。

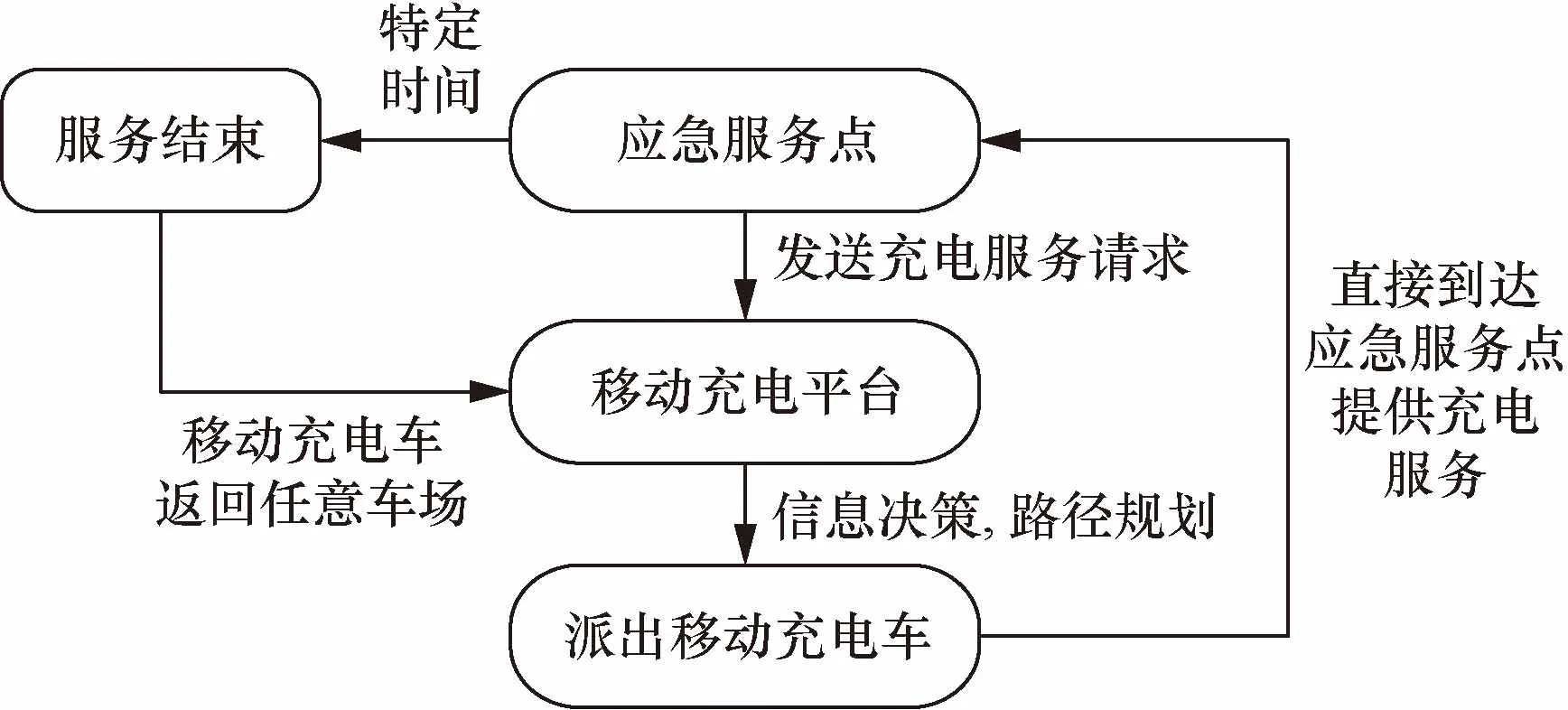
图1 移动充电服务流程图Fig.1 Flow chart of mobile charging service

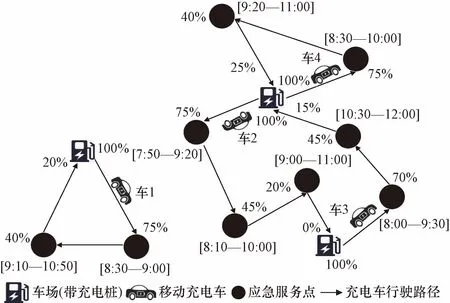
[]内的数字为该节点最佳时间窗;百分数为到达该节点剩余电量,表示到达上一节点剩余电量减去此节点服务电量和两节点间行驶消耗的电量图2 半开放式的多车场移动充电车路径优化问题示例Fig.2 An example of mobile charging vehicles path optimization problem on half-open multi depots

1.2 模型假设

为便于模型建立,做如下假设。

(1)车场和应急服务点地理位置、时间窗等信息均已知,所有节点间互联互通。

(2)移动充电车出发前,收到n个应急服务点预约的充电请求,途中不会产生新的应急服务需求点。

(3)不考虑车场建设成本,假设均已建设运营。

(4)移动充电车为同一车型,具有相同的电池容量、服务效率等参数。

(5)移动充电车行驶路线起止点均为车场,应急服务点不接受充电车的最终停靠。

1.3 符号说明

(1)集合。C为应急服务点编号集合,且C={1,2,…,n};D为车场编号集合,且D={1,2,…,m};N为所有节点集合,即N=D∪C;K为移动充电车集合,且K={1,2,…,k};kD为分配给车场D的移动充电车数量。

(2)参数。i、j为编号,应急服务点编号集合为C,车场编号集合为D;Q为移动充电车电池容量,包括为应急服务点提供服务的电量和自身行驶消耗的电量;M为极大值,作为惩罚进行约束;qi为应急服务点i所需电量;h为移动充电车电量消耗率;[ei,li]为应急服务点i的最佳时间窗;u为移动充电车充电服务效率;wk为移动充电车固定发车成本;CTransport为移动充电车单位运输成本;epu为车辆早到应急服务点的单位时间等待成本;lpu为车辆晚到应急服务点的单位时间惩罚成本;dij为节点i和节点j之间距离;tij为移动充电车从节点i行驶到节点j的时间。

(3)决策变量。xijk为0-1变量,移动充电车k从节点i行驶到节点j为1,反之为0;τi为到达节点i的时间;τbegin,i为在节点i开始服务的时间;yi为到达节点i的剩余电量。

1.4 模型建立

为解决移动充电平台投入运营成本高的问题,利用多车场间信息共享进行移动充电车的合理调度至关重要。基于多车场、应急服务点流量平衡、时间连续性、里程限制等约束条件,建立包括移动充电车启动成本、行驶成本和在应急服务点违反时间窗的惩罚成本在内的总成本最小的目标函数,如式(1)所示。模型建立如式(1)～式(23)所示。

minZ=Z1+Z2+Z3

(1)

式(1)中:Z为移动充电平台投入运营的总成本值。

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

τbegin,i=max(τi,ei),∀i∈C

(11)

τbegin,i=0,∀i∈D

(12)

τbegin,i+(tij+qiu)xijk-l0(1-xijk)≤τj,

∀k∈K;∀i∈N;∀j∈C;i≠j

(13)

式(13)中:l0为极大值,作为时间惩罚系数进行条件约束。

τbegin,i+tijxijk-l0(1-xijk)≤τj,

∀k∈K;∀i∈D;∀j∈C

(14)

τj≤τbegin,i+tij+qiu+M(1-xijk),

∀k∈K;∀i∈N;∀j∈N;i≠j

(15)

τj+M(1-xijk)≥τbegin,i+tij+qiu,

∀k∈K;∀i∈N;∀j∈N;i≠j

(16)

xijkqj≤yj≤yi-hdijxijk-qixijk+Q(1-xijk),

∀k∈K;∀i∈C;∀j∈N;i≠j

(17)

xijkqj≤yj≤Q-hdijxijk+Q(1-xijk),

∀k∈K;∀i∈D;∀j∈C

(18)

yj≤yi-hdij-qi+M(1-xijk),

∀k∈K;∀i∈C;∀j∈N;i≠j

(19)

yj+M(1-xijk)≥yi-hdij-qi,

∀k∈K;∀i∈C;∀j∈N;i≠j

(20)

yj≤Q-hdij+M(1-xijk),

∀k∈K;∀i∈D;∀j∈C

(21)

yj+M(1-xijk)≥Q-hdij,

∀k∈K;∀i∈D;∀j∈C

(22)

xijk∈{0,1},∀i∈N;∀j∈N;i≠j;∀k∈K

(23)

式(1)表示移动充电平台总成本最低的目标函数,包括式(2)移动充电车启动成本,式(3)行驶成本和式(4)在应急服务点最佳时间窗外提供服务产生的等待成本或惩罚成本;式(5)、式(6)表示每个车场派出和返回的充电车数量不超过该车场的最大车辆泊位,且松弛充电车必须返回原车场约束;式(7)表示派出服务的移动充电车不能直接从车场行驶到车场;式(8)保证每个应急服务点都被且仅被服务一次,并只能由一辆充电车提供服务;式(9)表示应急服务点进出平衡;式(10)表示每辆移动充电车最多属于一个车场,且最多允许服务一次;式(11)、式(12)表示移动充电车在节点i开始服务时间;式(13)、式(14)表示移动充电车到达各应急服务点的时间范围;式(15)、式(16)计算移动充电车到达各节点的准确时间值;式(17)、式(18)表示移动充电车到达各节点的剩余电量范围;式(19)～式(22)计算移动充电车到达各节点的剩余电量准确值;式(23)表示0-1决策变量。

2 遗传算法设计

遗传算法将问题初始解在染色体中进行编码,通过计算种群各个体适应度值,把适应度高的个体按比例保留到子代,经过交叉、变异等方式寻求更优解,能够快速求解复杂的组合优化问题,适合中大规模算例的启发式求解。故采用遗传算法对半开放式的多车场移动充电车路径优化模型求解,既能提高求解效率和求解质量,也能得到该问题的近似全局最优解。

2.1 编码规则

带时间窗的半开放式多车场移动充电车路径优化问题(HO-MDEVRP-TW)属于混合整数非线性规划问题,具有时间和空间双重维度求解难度,故采取自然数形式进行编码。染色体长度为n+k+3,其中,n为新能源汽车应急服务点数量,k为移动充电车数,3为车场数量。染色体编码示意图如图3所示。

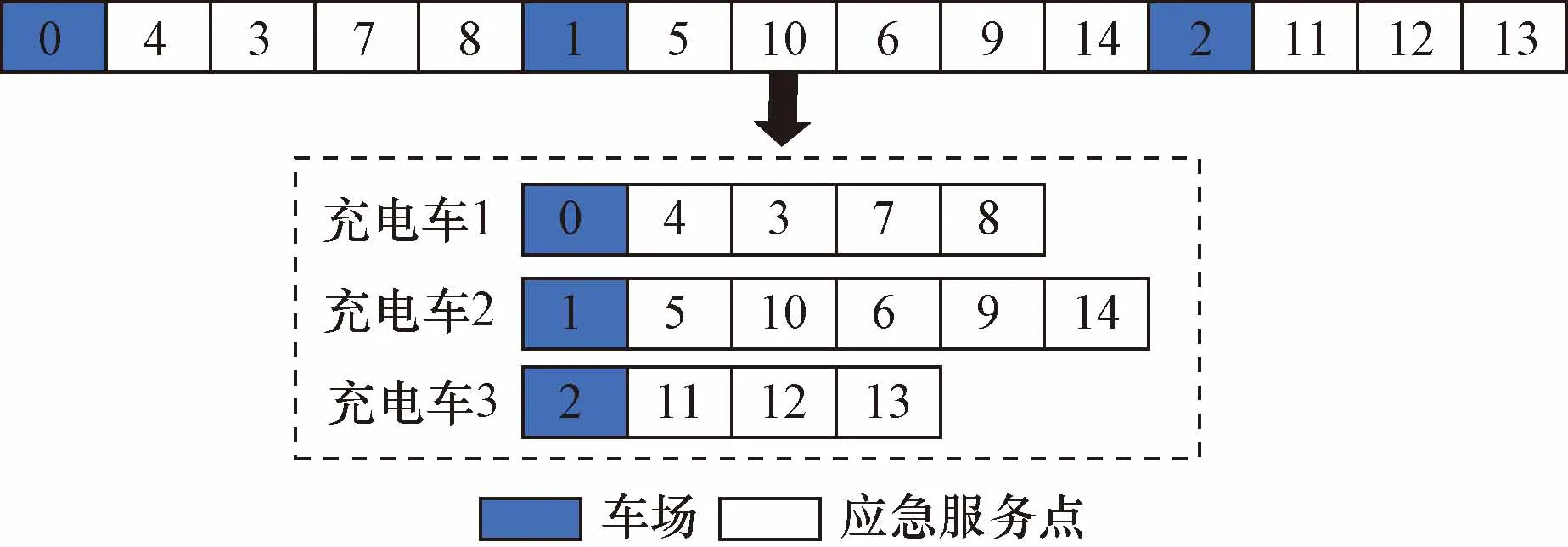
0～2表示3个车场编号;3～14表示移动充电车服务的应急需求点图3 染色体编码示意图Fig.3 Chromosome coding diagram

从染色体编码示意图(图3)可以看出,充电车1属于第一个车场,其服务路径为从车场0出发,服务应急需求点4、3、7和8;充电车2属于第2个车场,其服务路径为从车场1出发,服务应急需求点5、10、6、9和14;充电车3属于第3个车场,其服务路径为从车场2出发,服务应急需求点11、12和13。

2.2 精英保留策略

每次迭代结束,经过选择比较,将子代种群前50%优秀个体和父代种群前50%优秀个体运用精英保留策略进行融合,纳入精英库,确保每次迭代后子代种群能保留和父代种群相同的个体。通过轮盘赌策略对精英库中被选择个体执行再次筛选,确保精英库保存全部优秀个体,同时加快算法收敛速度。

2.3 交叉操作

从精英库中任意选择两条染色体作为父代个体,在选中的父代个体上随机选择一条子路径,记录子路径的个数n1。通过改进交叉算子对选中的两条染色体进行交叉操作,将选择的子路径在子代染色体中前置,未访问节点多次随机插入车辆,打断为1～(n1-1)条子路。选择生成的子路径中总成本最小的,添加到子代染色体片段之后,形成完整的子染色体。

假设有两个父代个体,如图4所示。

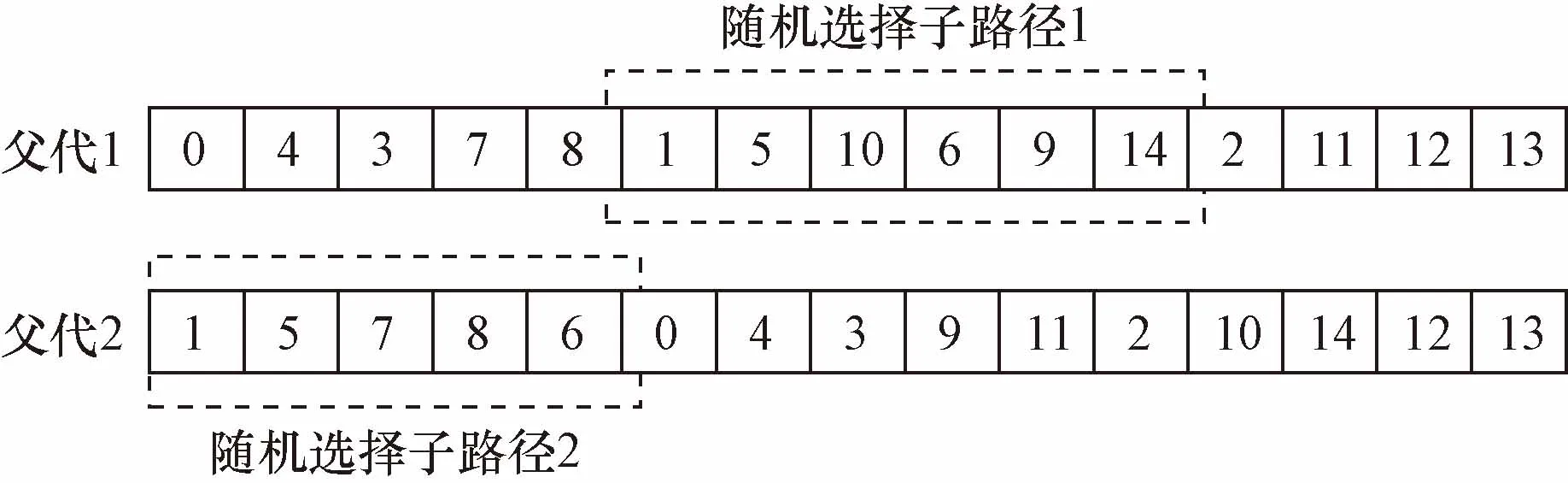
图4 父代染色体片段Fig.4 Parental chromosome fragment

经交叉操作得到两个子代个体,如图5所示。

图5 子代染色体片段Fig.5 Progeny chromosome fragment

2.4 变异操作

随机在染色体上选取两个基因位点,如图6中的8和14所示,采用2-opt算法对该染色体进行局部优化,将两位点之间的基因片段反转并接回原来的位置。如果变异后染色体总成本小于变异前染色体总成本,则用变异后染色体代替变异前染色体,否则保持原染色体不变。染色体变异如图6所示。

图6 染色体变异示意图Fig.6 Chromosome variation diagram

3 算例分析

3.1 算例描述

由于半开放式的多车场移动充电车联合服务模式下相关约束较多,且具有时间惩罚成本和半开放式的特点,目前没有通用的算例集。选用Solomon设计的VRPTW标准算例中的R102算例,根据联合服务的特点对其进行修改,生成3个车场、8个应急服务点的小规模测试算例(3D-8C)如表1、表2所示,3个车场、30个应急服务点的中规模测试算例(3D-30C)如表3所示。在Windows10操作系统、16 GB内存、2.60 GHz的Intel(R)Core(TM)i5-11400处理器上,通过Python3.7编写分支定界法和遗传算法实现模型求解。

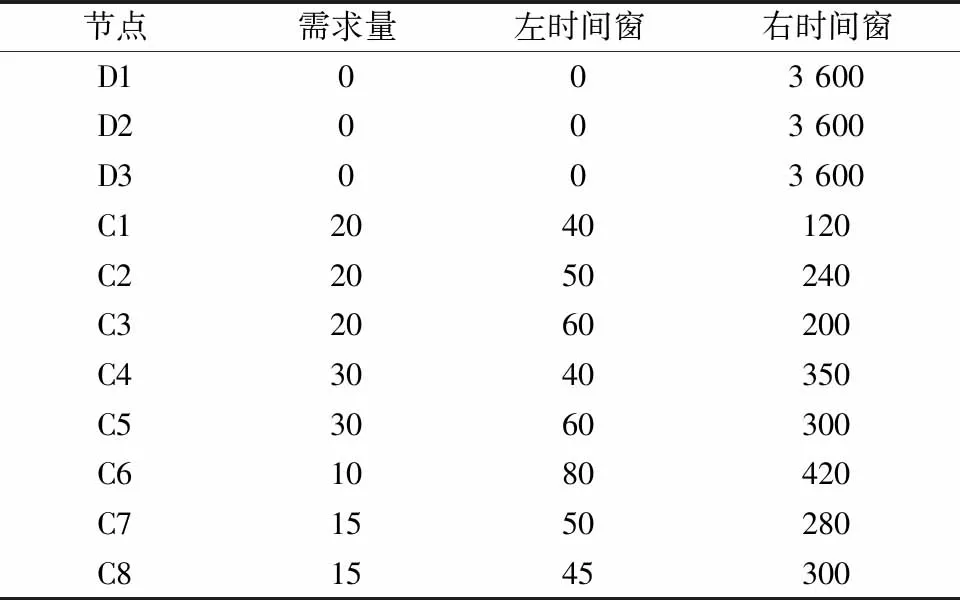
表1 3D-8C算例各节点需求量及时间窗Table 1 3D-8C instance demands and time windows of each node

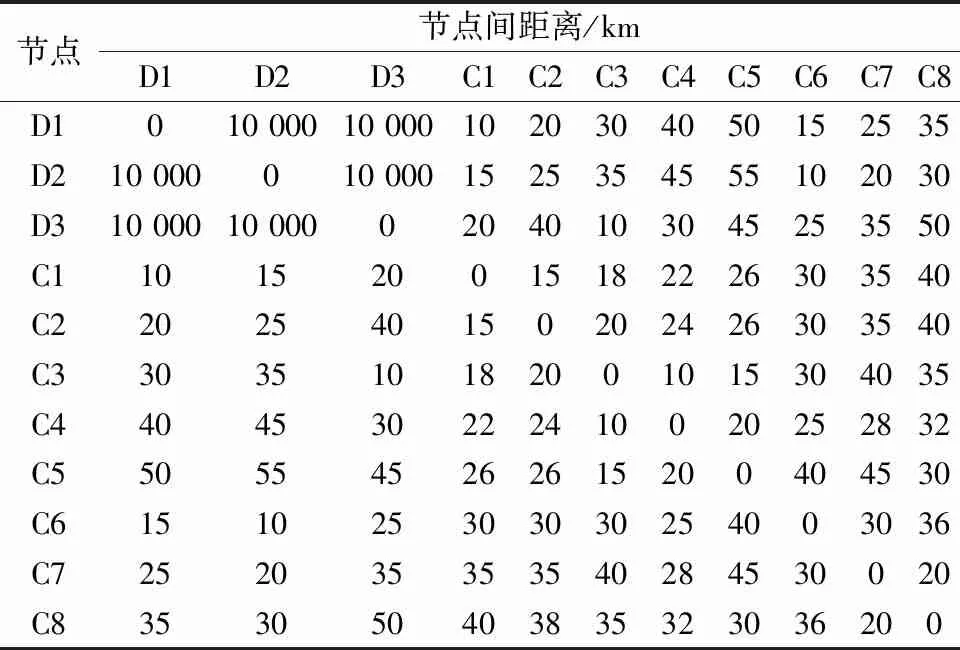
表2 3D-8C算例各节点间距离Table 2 3D-8C instance distances between nodes

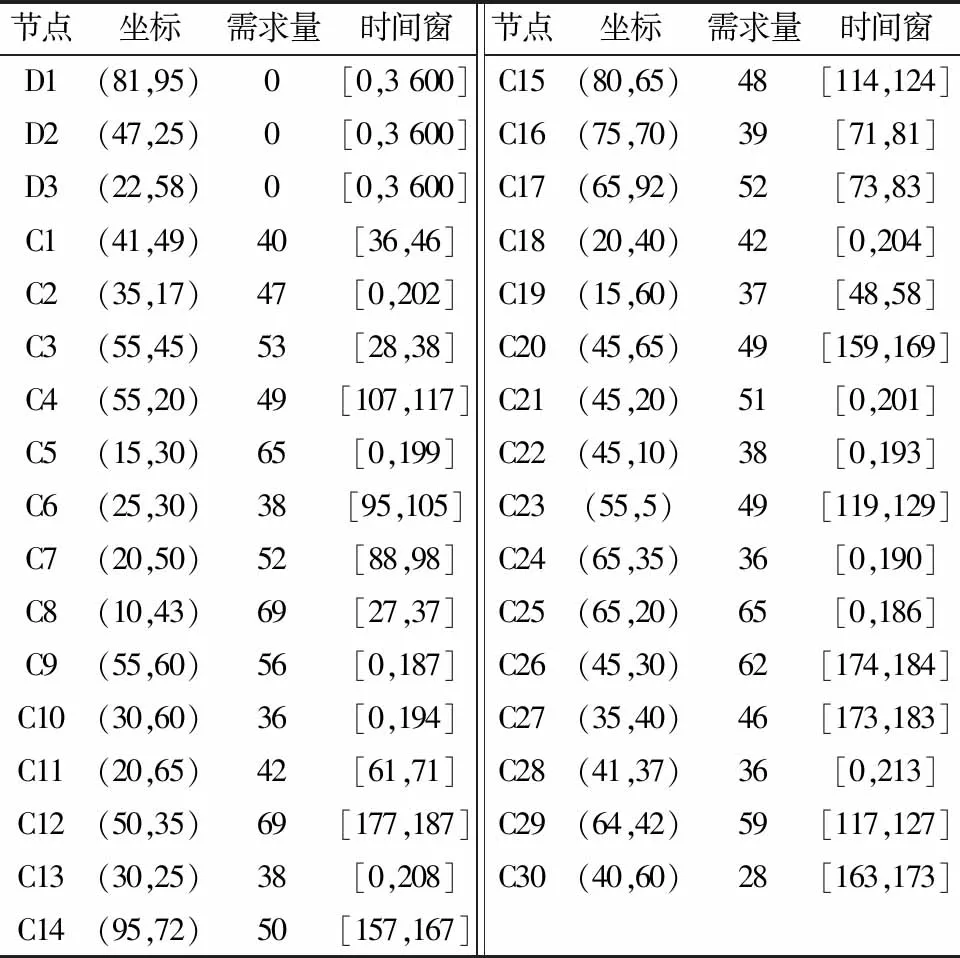
表3 3D-30C各节点坐标、需求量及时间窗Table 3 3D-30C coordinates,demands and time windows of each node

3.2 算法比较与分析

采用分支定界法对3个车场、8个应急服务点(3D-8C)的小规模构造算例进行精确求解,验证所建模型准确性。对比遗传算法的求解时间和计算结果可知,遗传算法在小规模算例下能够得到和分支定界法相同的精确解,表明遗传算法具有较好的求解质量,且对中大规模算例求解更具时间优势。结果如表4所示。

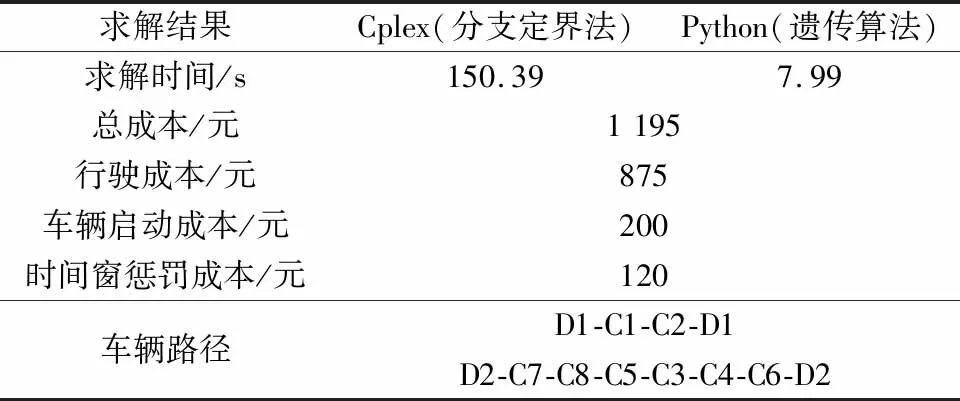
表4 3D-8C算例结果Table 4 Result of 3D-8C instance

根据算例节点数,经过多次实验,模型相关参数设置如下:种群数量400,交叉概率0.90,Q=300,h=1,u=1,wk=100,CTransport=5,epu=2,lpu=3,迭代次数设为250次。遗传算法求解R102算例的10次运行结果及每次运行得到的解与10次中最优解偏差(gap)值如表5所示。最优解如表6所示。

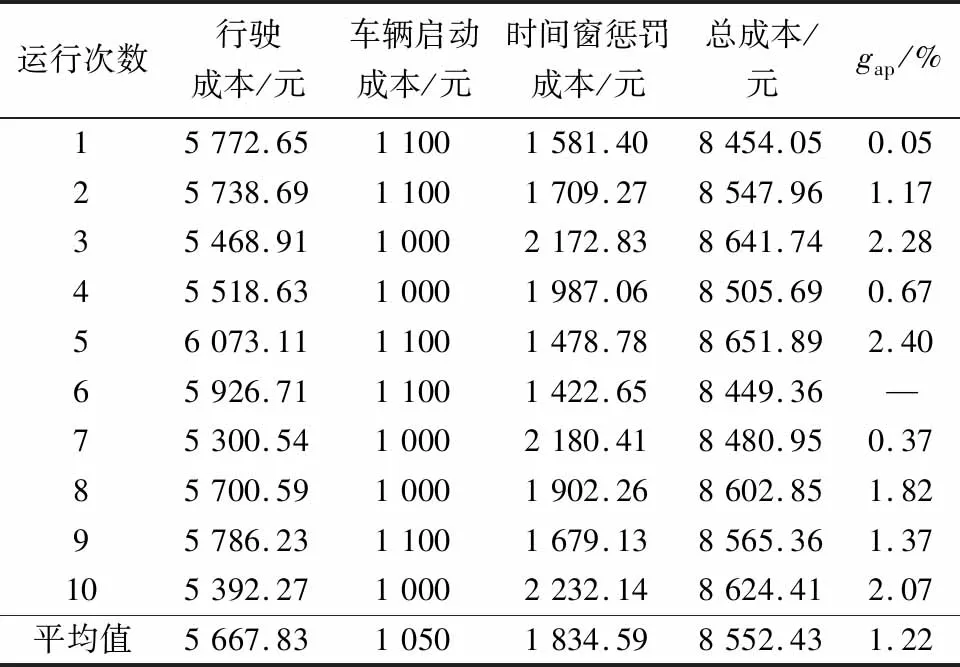
表5 3D-30C算例下遗传算法求解10次结果Table 5 Results were solved 10 times by genetic algorithm under 3D-30C instance

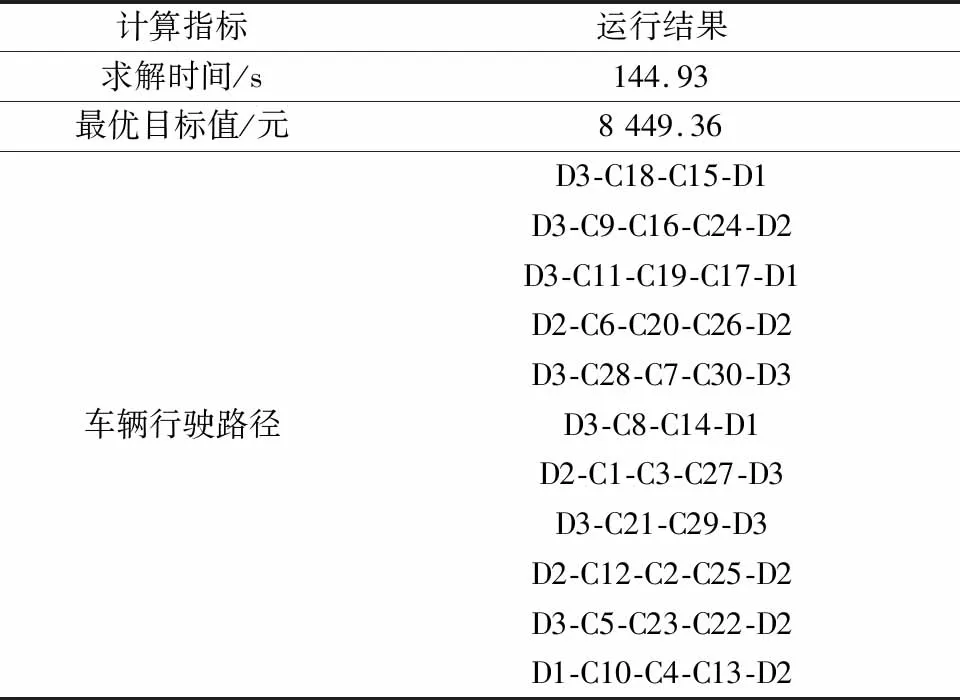
表6 3D-30C算例下遗传算法求得的最优解Table 6 The optimal solution was obtained by genetic algorithm under 3D-30C instance

3D-30C算例运行10次的目标均值为8 552.43元,其中行驶成本均值为5 667.83 元,车辆启动成本均值为1 050 元,时间惩罚成本均值1 834.59 元。3D-30C算例运行10次的总成本最优值为8 449.36元,每次运行目标值与最优目标值的平均gap为1.22%,最大gap值为2.40%,充分说明遗传算法求解的稳定性。从表6可以看出,3个车场共派出11辆移动充电车满足30个应急服务点的全部充电需求,其中有4辆充电车返回原车场,7辆车由于距离因素,返回其他车场。

最优解的算法迭代过程如图7所示。行驶路线如图8所示。通过迭代图(图7)可知,算法在第125代左右向最优解收敛,能够跳出局部最优解,说明遗传算法具有较好的求解质量和求解效果。

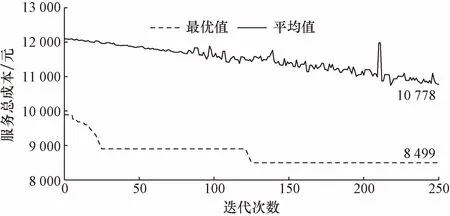
图7 3D-30C算例最优解迭代图Fig.7 Iteration diagram of optimal solution under 3D-30C instance

图8 3D-30C算例最优解路线图Fig.8 Routing diagram of optimal solution under 3D-30C instance

3.3 敏感性分析

为明确带时间窗的半开放式多车场移动充电车联合服务路径优化问题(HO-MDEVRP-TW)的特点,设计了传统带时间窗的单车场(EVRP-TW)独立服务模型进行对比分析,EVRP-TW模型在HO-MDEVRP-TW模型的基础上,将多车场集合D修改为一个车场即可。在相同的参数假设和系统运行环境下,通过不同客户分布类型(R为随机分布、C为集中分布、RC为混合分布)的规模算例,运用遗传算法对其进行10次求解计算均值。不同算例的成本变化情况如表7所示。

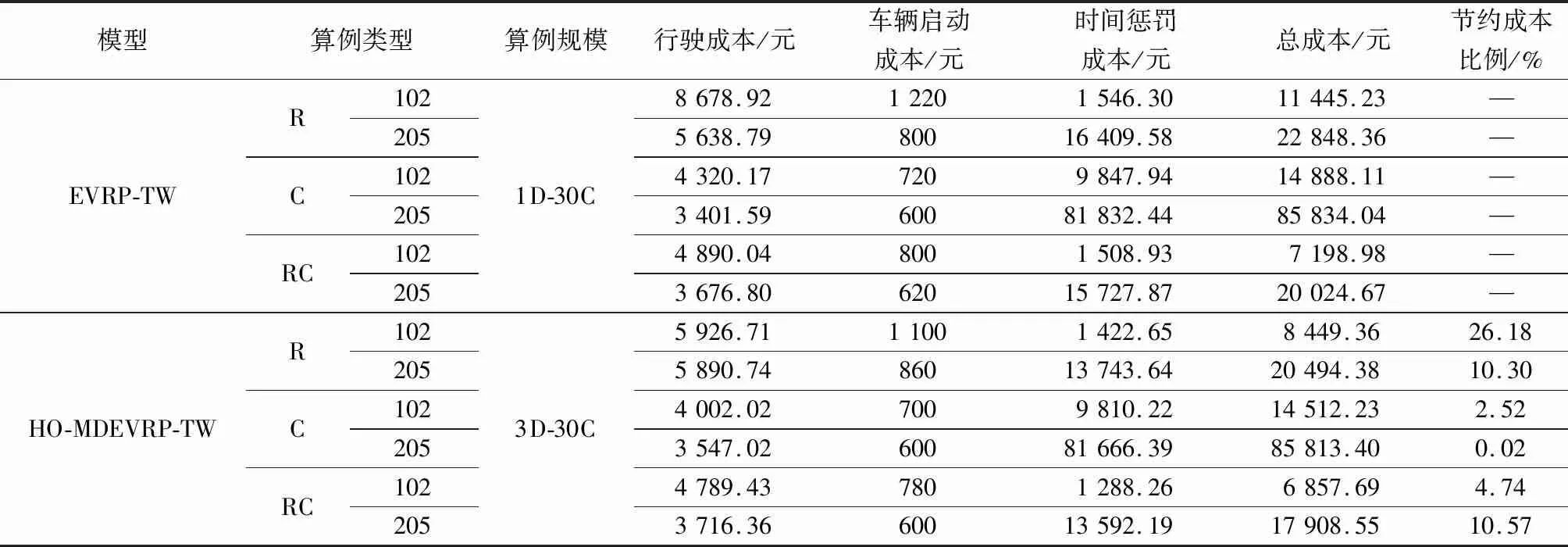
表7 EVRP-TW和HO-MDEVRP-TW的成本变化情况Table 7 Changing situation of EVRP-TW and HO-MDEVRP-TW costs

对比HO-MDEVRP-TW和EVRP-TW算例运行结果(表7),可以看出,半开放式多车场联合服务比单车场独立服务在R102算例和R205算例分别节约26.18%和10.30%的总成本,主要体现在移动充电车为应急服务点提供充电服务时行驶成本的节约和在应急服务点违反时间窗的时限减少;在C102算例和C205算例分别节约2.52%和0.02%的总成本,主要体现在移动充电车为应急服务点提供充电服务时行驶成本的节约;在RC102算例和RC205算例分别节约4.74%和10.57%的总成本,主要体现在移动充电车提供充电服务时在应急服务点违反时间窗的时限减少。比较结果表明,半开放式的多车场联合服务能够大幅减少单车场独立服务模式下由于充电车频繁往返始发中心产生的重复行驶路径;移动充电平台提供的移动充电车在满足全部应急服务点充电需求的前提下,能够显著降低包括移动充电车为应急服务点提供充电服务的车辆启动成本、行驶成本和在应急服务点违反时间窗的惩罚成本在内的总成本,从而为移动充电平台带来更大的收益;移动充电平台在R型算例和RC型算例下节约成本较为明显,说明半开放式的多车场联合服务对随机分布客户群体和混合分布客户群体的需求能够做出更快响应,体现了将移动充电车置于半开放式多车场联合服务场景的优越性。

4 结论

考虑新能源汽车应急服务点分布随机性特点,将移动充电车置于半开放式的多车场联合服务场景,构建了半开放式的多车场移动充电车路径优化模型,利用分支定界法和遗传算法对模型求解,验证了模型的正确性和算法的有效性。通过三种客户分布类型的算例对半开放式的多车场联合服务和单车场独立服务两种模型对比分析,得出以下结论。

(1)半开放式的多车场联合服务能够为移动充电车提供更多的路径选择,减少移动充电车的行驶里程,有效提高移动充电平台的服务效率,降低平台的运营成本。

(2)半开放式的多车场联合服务能够适用新能源汽车应急服务点分布随机性特点,在R型和RC型算例下显著节约移动充电平台的总运营成本,为移动充电平台规划合理的服务路径,使得移动充电车和多车场设施等资源得到充分利用。

在后续的研究中,可考虑顾客动态服务需求以及多车场选址等因素,建立更加符合实际场景的应用模型,为移动充电车做出合理的路径规划,给移动充电平台提供科学的决策价值。