两个含时变系数的高维非线性演化方程新型孤子和多波解

秦宇昕 ,柳银萍 ,徐桂琼

（1.华东师范大学 计算机科学与技术学院,上海 200062;2.华东师范大学 数学科学学院,上海 200241;3.上海大学 管理学院,上海 200444）

0 引言

非线性演化方程,特别是高维非线性演化方程,可用于描述自然界中形形色色的非线性现象.因此,非线性演化方程解法的研究始终是数学物理领域的重要课题.近几年,构造高维非线性演化方程的复杂波解受到了一些学者的重视和青睐[1-7].目前已经有很多关于常系数高维非线性演化方程不同类型波解的研究成果[8-14].然而,由于自然界中介质的不均匀性,含有变系数的非线性演化方程往往能更好地描述科学和工程背景下的真实特征,构造这类方程的新型波解是非常有意义的工作[15-18].本文通过引入特定的非线性行波变换,构造了两个含时变系数的高维非线性演化方程的新型高阶和多波相互作用解.

本文结构为: 第1 章针对(3+1) 维Boiti-Leon-Manna-Pempinelli(BLMP) 方程,引入特定的非线性行波变换,构造了其新型多波相互作用解;第2 章通过引入新的非线性行波变量,构造了(2+1)维圆柱Kadomtsev-Petviashvili(cylindrical Kadomtsev-Petviashvili,cKP) 方程的马蹄形孤子、呼吸子和lump 波解之间的高阶相互作用解;第3 章总结了本文工作的创新点,并得出了结论.

1 含时变系数的(3+1) 维BLMP 方程的新型多波相互作用解

(3+1) 维BLMP 方程

诞生于2012 年[19],其中u=u(x,y,z,t) ,x,y,z为空间变量,t为时间变量.该方程可作为描述不可压缩流体的模型.当z=0 时,该方程可表示沿y轴传播的黎曼波与沿x轴传播的长波间的相互作用.关于式(1)的精确波解和相关性质的研究,目前已有了一些良好的成果,如已有文献报道了其有理解、非行波解和其他相互作用波解[20-24].

文献[25]将式(1)扩展至含有时变系数的BLMP 方程

式(2)中:αβ,是实常数;g(t)是一个依赖于时间t的变系数.文献[25]讨论了当g(t)为任意函数时,式(2)的Painlevé可积性,并构造了其孤子解.目前,已报道的式(2)的精确解都是基于线性行波变换的行波解,本文将通过引入非线性行波变换,构造该方程的马蹄形孤子、周期波和lump 波解之间的新型多波相互作用解.

对式(2),通过Painlevé截断展开法可以得到变换

其中f=f(x,y,z,t).将式(3)作用于式(2)中,并化简之,得到关于函数f及其导数的方程

直接代数方法是构造非线性微分方程精确解的一种典型方法,该方法通过假设待求的解为特定先验形式,进而将非线性微分方程的求解问题转化为非线性代数方程组的求解问题.然而,对于高阶波解或复杂的相互作用解,本文通过转化得到的非线性代数方程组往往过于庞大,难以直接求解.为了解决这一计算瓶颈,本文提出了一种逐步求解此类大规模甚至超大规模非线性代数方程组的策略,称之为“继承求解”策略.该策略的主要思路是基于已知的低阶解(即初始解),进一步构造更高阶的解.由于利用直接代数法得到的非线性代数方程组通常具有很大的冗余度,因此基于这种策略往往可以大大简化待求解的大规模非线性代数方程组.需要说明,为了简化计算,下文中取g(t) 为特定的形式,如令g(t)=1/t,对于其他形式的g(t),计算过程完全类似.

为利用直接代数方法和继承求解策略来构造高阶波解,首先考虑其低阶解,如式(2)的1-孤子解,相应的辅助函数

为非线性行波变换,δ1,k1,r1,s1,p1,ω1,c1,qi(i=1,2) 为未知参数.

将解的先验假设形式(式(5))代入式(4),合并同类项,并令每一项的系数分别为零,得到一个包含16 个方程和9 个变量的非线性代数方程组.由于该方程组规模不大,直接求解可得到一组解

其中ξi(i=1,2,3) 的形式与式(5)中的相同.限于篇幅,其计算过程和解的表达式不再赘述.所获得的1-孤子解,2-孤子解,3-孤子解的图象分别如图1(a)—(c)所示,图1(d)—(f)分别是相应的密度图,其中各坐标轴单位均为1.图1 的作图参数值为β=-1,c1=5,δ2=3,k2=1/3,c2=-10,c3=25,其余参数皆为 1 .从图1 中可明显地看出所获得的孤子呈现马蹄形状.

图1 式(2)的马蹄形孤子解和密度图Fig.1 Horseshoe-like solitons for Equation(2) and the density maps

为了获得式(2)更复杂的多波解,如构造其1-lump、1-孤子和雅可比椭圆函数之间的相互作用解,可假设辅助函数

为行波变量,其中δi,ki,ri,si,pi,ωi,ci,qi是未知参数,模R满足R2≤1.可以看出该行波变量是非线性的.将假设式(8)代入式(4),合并同类项,并令不同次幂项的系数为零,得到一个包含5 342 个方程和32 个变量的非线性代数方程组.该代数方程组规模过大,难以直接求解,因此将解(6)作为初始解以采用继承求解策略.求解简化后的非线性代数方程组,得到如下一组解:

将解(9)依次代入式(8)和式(3),即可获得式(2)的1-lump、1-孤子和雅可比椭圆函数的多波相互作用解.该解在不同时刻的演化图象如图2(a)—(d)所示,图2(e)—(h)分别是相应的密度图.图2 的作图参数值为β=-1 ,R=1/10,δ1=1/2,k1=5/4 ,c1=30 ,q1=6 ,δ2=1/2 ,s2=-1,c2=30,q3=5,k4=-7/6,s4=1/2,其余参数值皆为1.可以看出,孤子的方向和孤子卷曲的程度随时间而变化.特别是当t=0 时,孤子和lump 波都退化为线形波.

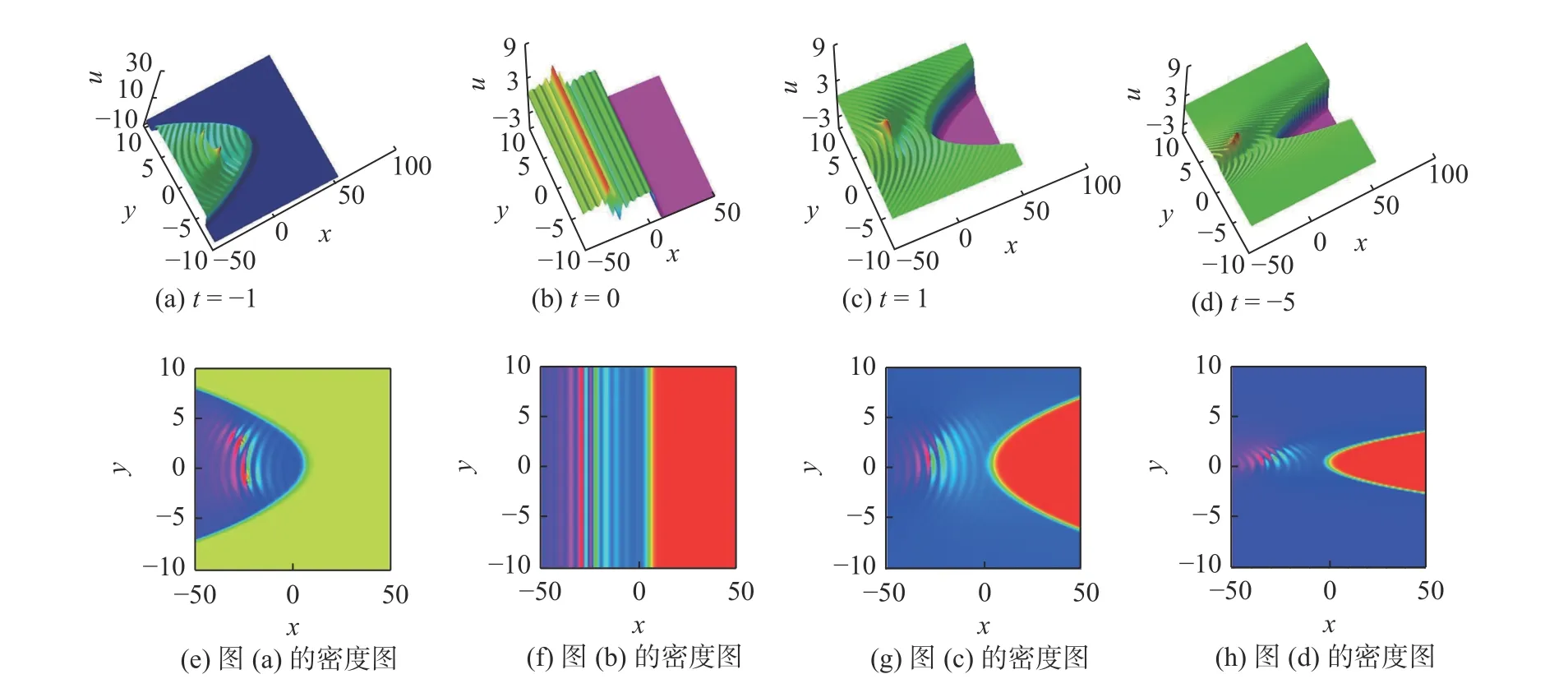
图2 式(2)的1-lump,1-孤子和雅可比椭圆函数的多波相互作用解和密度图Fig.2 Multiwave-interaction solutions of 1-lump,1-soliton,and the Jacobi elliptic cosine function for Equation(2)and the density maps

若假设辅助函数

其中δi,ki,ri,si,pi,ωi,ci,qi是未知参数,模R2≤1,便可以进一步构造式(2)的1-lump、3-孤子和雅可比椭圆函数的高阶相互作用解,这里行波变量

仍然是非线性的.将解(6)作为初始解,基于继承求解策略,可获得如下一组解:

将解(11)代入辅助函数式(10)和式(3),得到式(2)的1-lump、3-孤子和雅可比椭圆函数的三波相互作用解.此外,通过共轭参数赋值[26],可以将其中的2-孤子转换为1-呼吸子.这样,该三波相互作用解将转换为1-lump、1-呼吸子、1-孤子和雅可比椭圆函数间的四波相互作用解,如图3 所示.图3(a)为式(2)的1-lump,3-孤子和雅可比椭圆函数的三波相互作用解,作图参数值为β=-1,R=1/10,s2=-1,k6=-1/2,c1=30 ,c2=30 ,c3=-15 ,δ4=3,k4=1/3 ,c4=-13 ,c5=15 ,q1=101,q9=100.图3(b)为式(2)的1-lump,1-呼吸子,1-孤子和雅可比椭圆函数的四波相互作用解,作图参数为k1=1/5 ,c1=4,k2=1/5 ,c2=4 ,δ3=2,k3=(2/3)i(i 为虚数单位),c3=-2 ,δ4=2 ,k4=(-2/3)i,c4=-2,δ5=2/3 ,q1=21 ,q9=20,其余参数值皆为1.图3(c)和 图3(d)是分别对应于图3(a)和图3(b)的密度图.

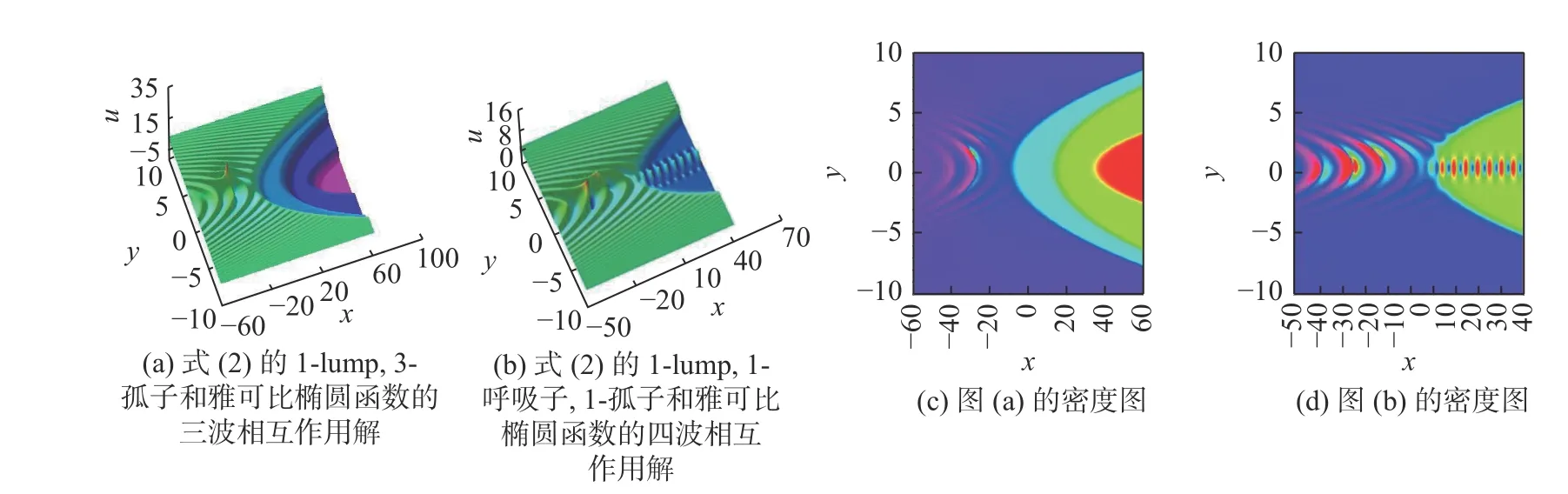
图3 式(2)的三波和四波相互作用解以及密度图Fig.3 Three-wave-interaction solution and four-wave-interaction solution for Equation(2) and the density maps

2 (2+1) 维cKP 方程的马蹄形孤子、呼吸子和lump 波解之间的高阶相互作用解

Hirota 方法是构造非线性演化方程孤子解的最有效方法之一.在得到孤子解后,便可以通过共轭参数法进一步计算呼吸子解[26].同样地,通过长极限法可由孤子解计算lump 解[26].本章将通过分解孤子解来构造以下cKP 方程的新型多波相互作用解：

其中u=u(x,y,t),γ是实常数.在研究分层介质中的内波以及具有压力效应和横向扰动的磁化等离子体时,式(12)于1978 年被首次推导出[27].已有文献报道了其孤子解、有理波解以及1-lump 与孤子间的相互作用解等[28].本文通过引入一特定非线性行波变换来求解式(12)的马蹄形孤子、呼吸子和lump 波解之间的高阶相互作用解.

通过引入变换

其中f=f(x,y,t) ,式(12)被转换为关于函数f及其导数的方程：

其中δi,si,ri,ki,ωi,ci为未知实参数.首先以此为基础构造式(12)的孤子解.根据简单Hirota 方法,孤子解可以表示为指数函数的组合形式,例如,1-孤子和2-孤子的辅助函数分别具有形式:

综上所述,可以很容易计算出该方程的1-孤子和2-孤子的f表达式,相应的行波变量具有形式

上文提到,在获得孤子解之后,可继续通过共轭参数赋值将2-孤子转换为1-呼吸子,也可利用长极限法和共轭参数赋值,将2-孤子转换为1-lump 波.基于此,可将N分解为N=2m+2n+l,其中m、n及l均为自然数.将N- 孤子解中最前面的 2m-孤子转换为m-lump 波,将中间的 2n-孤子转换为n-呼吸子,并保持最后的l-孤子不变.由此可将N-孤子解分解转换为m-lump、n-呼吸子和l-孤子间的三波相互作用解,为简单起见,将这种解简记为mL-nB-lS.需要说明,当m、n或l为零时,所获得的多波相互作用解可退化为两波相互作用解,甚至单波解.

接下来以N=5 为例来说明如何通过分解孤子解来构造不同波之间的相互作用解.首先,可将N拆分为两个自然数之和,例如,令N=2+3,以此来计算1-lump 和3-孤子间的双波相互作用解.根据长极限法,求得关键参数

其中∗表示取共轭.将式(18)代入式(13),即可得到式(12)的1L-3S 双波相互作用解.

接下来,通过共轭参数赋值,可将中间的 2- 孤子进一步转化为 1- 呼吸子,即将N重新拆分为N=2+2+1.如此,便可以计算式(12)的1L-1B-1S 三波相互作用解,其相应的辅助函数为

其中的ξiR表示取行波变量ξi的实部.将辅助函数f1L-1B-1S代入变换式(13),最终得到了式(12)的1L-1B-1S 解.获得的上述3 种解及其密度图如图4 所示.图4(a)为式(12)的5-孤子解,作图参数值为k1=1/10,r1=1/10 ,c1=0 ,k2=1/10,r2=3/10 ,c2=0,k5=1/10,k3=1/10 ,r3=2/5 ,c3=0,k4=1/10,r4=1/5 ,c4=0,r5=1/2 ,c5=0 .图4(b)为 式(12)的3-孤子与1-lump 的相互作用解,作图参数值为k1R=0,k1I=1/7 ,r1I=0 ,c1R=0 ,c1I=0 ,δ3=3,k3=1/10 ,r3=1/10 ,c3=10,δ4=3,k4=1/10,r4=3/10 ,c4=10 ,δ5=3,r5=1/2 ,c5=10 .图4(c)为式(12)的1-孤子,1-呼吸子与1-lump 的相互作用解,作图参数值为k1R=0,k1I=1/7 ,r1I=0 ,c1R=5 ,c1I=10 ,k2R=0,k2I=1/10,r2R=3/2 ,r2I=0 ,c2R=0 ,c2I=0 ,δ5=10,k5=1/10,r5=1/10 ,c5=15,t=1/10,其余参数值皆为1.其中kiR,ciR,riR分别表示ki,ci,ri的实部;kiI,ciI,riI分别表示ki,ci,ri的虚部.图4(d)—(f)是分别对应于图4(a)—(c)的密度图.

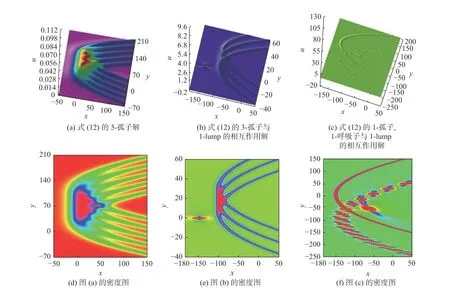
图4 式(12)的1L-1B-1S 三波相互作用解和密度图Fig.4 Three-wave-interaction solution of 1L-1B-1S for Equation(12) and the density maps

基于上述孤子分解思想,可以计算出式(12)任意高阶的马蹄形孤子、呼吸子和lump 波解间的相互作用解.图5 展示了几个具有代表性的高阶及多波解,限于篇幅,这里省略解表达式.相应的参数值如表1 所示.

表1 图5 的参数表Tab.1 Parameters of Figure 5

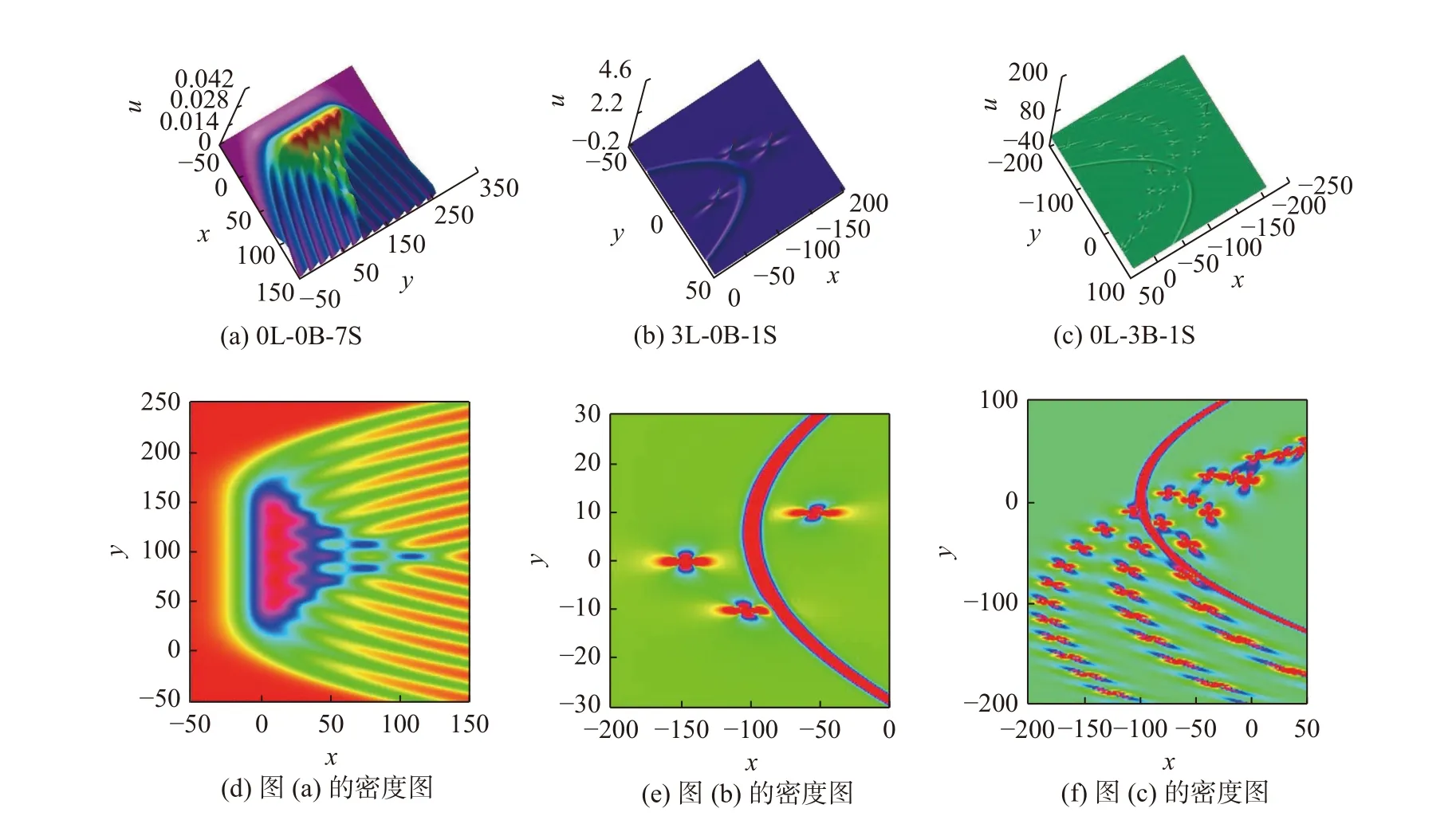
图5 式(12)的高阶及多波相互作用解和密度图Fig.5 Higher-order and multiwave-interaction solutions for Equation(12) and the density maps

3 结论

N-孤子分解算法和继承求解策略是笔者课题组在构造常系数非线性演化方程的高阶行波解时提出的,一般行波变量都是线性函数.本文通过引入非线性行波变量,并将该算法应用于高维变系数非线性演化方程,构造了它们的新型孤子解及其他的波解,包括不同波之间的相互作用解等.由此可见,本文应用的算法和求解技巧具有普适性,也可以很好适用于求解其他高维非线性演化方程.